A plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index μ is filled up to a height h in the vessel. There is a fish at a height h/2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel.
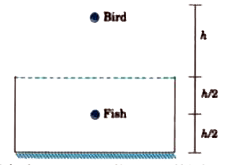
(a) Calculate apparent distance of bird as seen by the fish.
(b) Calculate apparent distance of image of bird in mirror as seen by the fish.
(c) Calculate apparent distance of fish as seen by the bird.
(d) Calculate apparent distance of image of fish in the mirror as seen by the bird.
Video Solution
Text Solution
First of all we should know the following formula :
apparent depth=real depthμ
Here μ is the refractive index of medium of object with respect to medium of observer. Hence if μ is refractive index of water with respect to air then 1/μ will be the refractive index of air with respect to water.
As a next step for ease of calculation we can first reflect images from plane mirror without considering shift due to changing medium and then separately we can consider the shift.
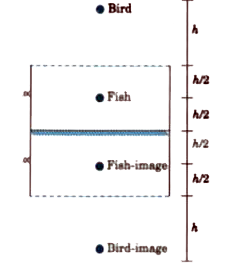
(a) Apparent distance of bird as seen by the fish
=h2+h1/μ=h2+μh=h(12+μ)
(b) Apparent distance of image of bird as seen by the fish =3h2+h1/μ=3h2+μh=h(32+μ)
Note that image of water is also treated as water.
(c ) Apparent distance of fish as seen by the bird
=h+h/2μ=h(1+12μ)
(d) Apparent distance of image of fish as seen by the bird =h+3h/2μ=h(1+32μ)
|
Updated on:21/07/2023
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Very Short Answer Questions)82videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Additional Questions)22videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT (Exemplar Problems Subjective Questions) (Very Short Answer Type Questions)11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Practice Problems
- Question 1 - Select One
A bird in air is at a height ‘y’ from the surface of water. A fish is at a depth ‘x’ below the surface of water. The apparent distance of fish from the bird is (The refractive index of water is n )
Ax+yμBμx+yCxμ+yDxμ−y - Question 1 - Select One
A plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observes P and its image in the mirror. The apparent distance between two will be
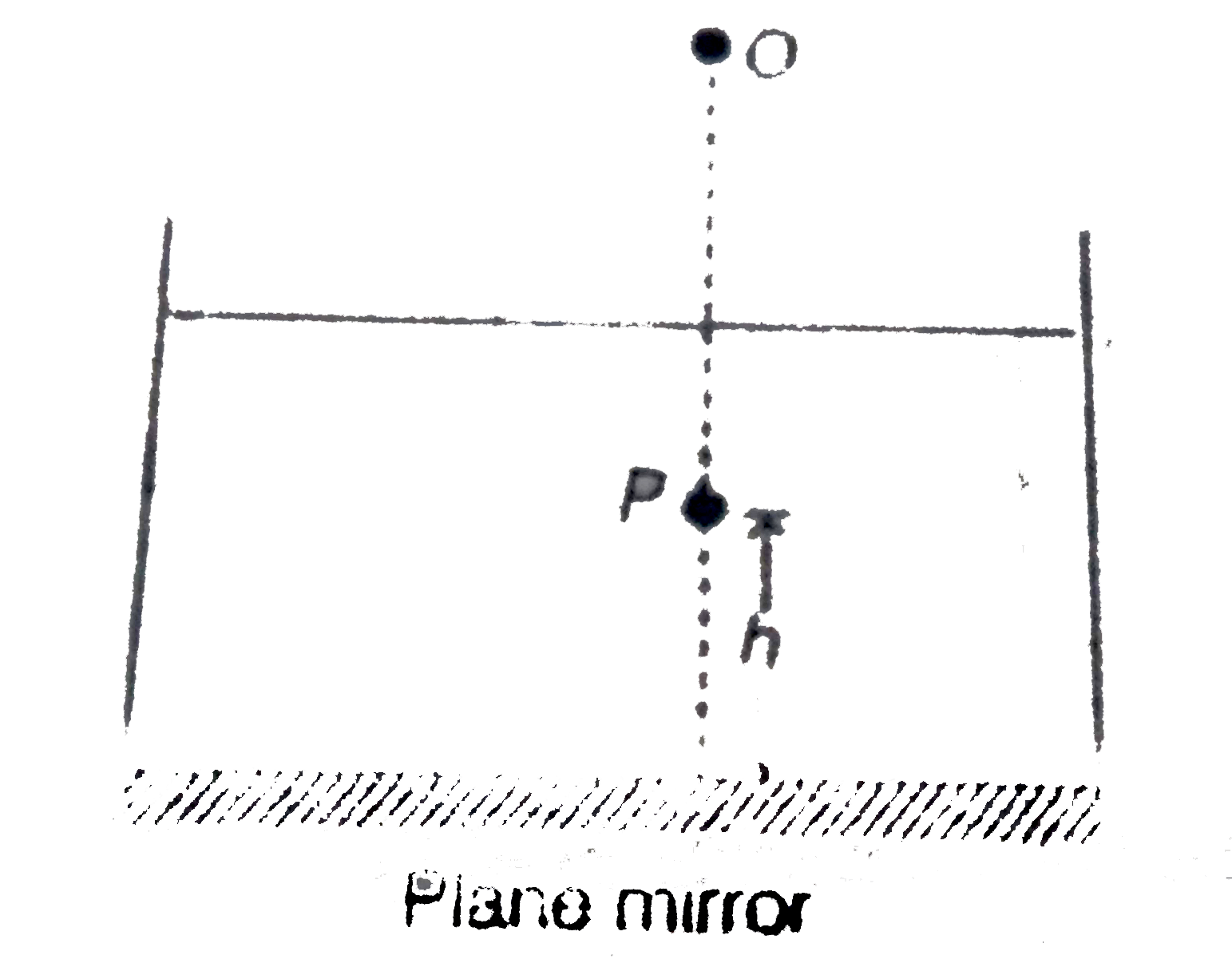 A2μhB2hμC2hμ−1Dh(1+1μ)
A2μhB2hμC2hμ−1Dh(1+1μ) - Question 1 - Select One
There is a hole at the bottom of a large open vessel. If water is filled upto a height h, it flows out in time t. if water is filled to a height 4h, it will flow out in time
A4 tBt/4Ct/2D2t - Question 1 - Select One
A point source of light is placed at the bottom of a vessel which is filled with water of refractive index μ to a height h. If a floating opaque disc has to be placed exactly above it so that the source is invisible from above, the radius of the disc should be-
Ah√μ−1Bh√μ2−1Chμ2−1Dμh√μ2−1 - Question 1 - Select One
A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
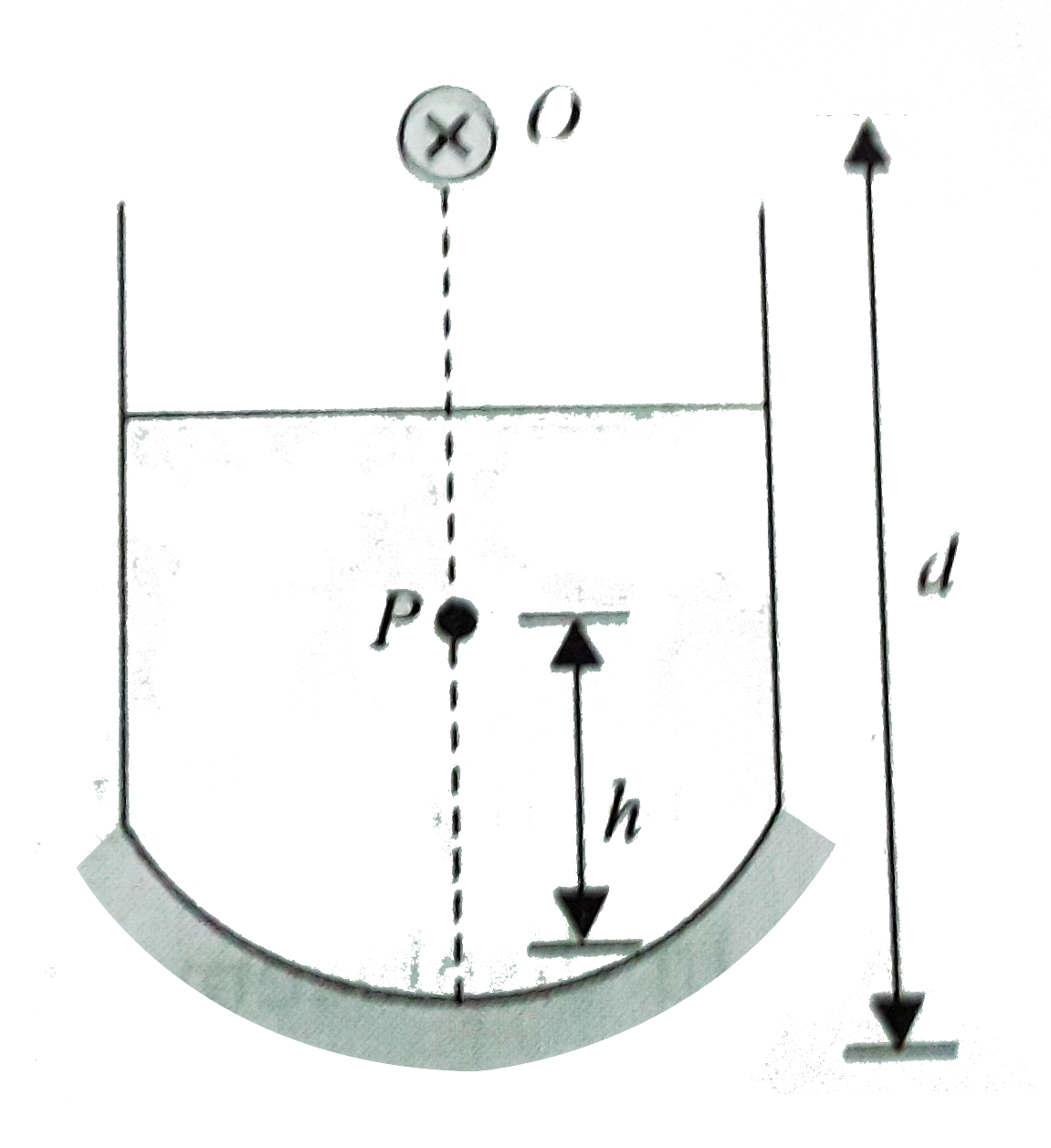 Ah(1−1μ)B2hμ−1CzeroD2hμ
Ah(1−1μ)B2hμ−1CzeroD2hμ - Question 1 - Select One
Two immiscible liquids of refractive index √2 and 2√2 are filled with equal height h in a vessel. Then apparent depth of bottom surface of the container given that outside medium is air
A3√2h4B3h4C3h2D3h4√2 - Question 1 - Select One
A bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
A2.25mB3.33mC4mD4/3m - Question 1 - Select One
A bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
Ah1+h2Bh1+h2μCμh1+h2Dμh1+μh2
Similar Questions
In Fig. a plane mirror lies at a height h above the bottom of a beaker containingwater (refractive index μ) upto a height f. Find the position of the image of the
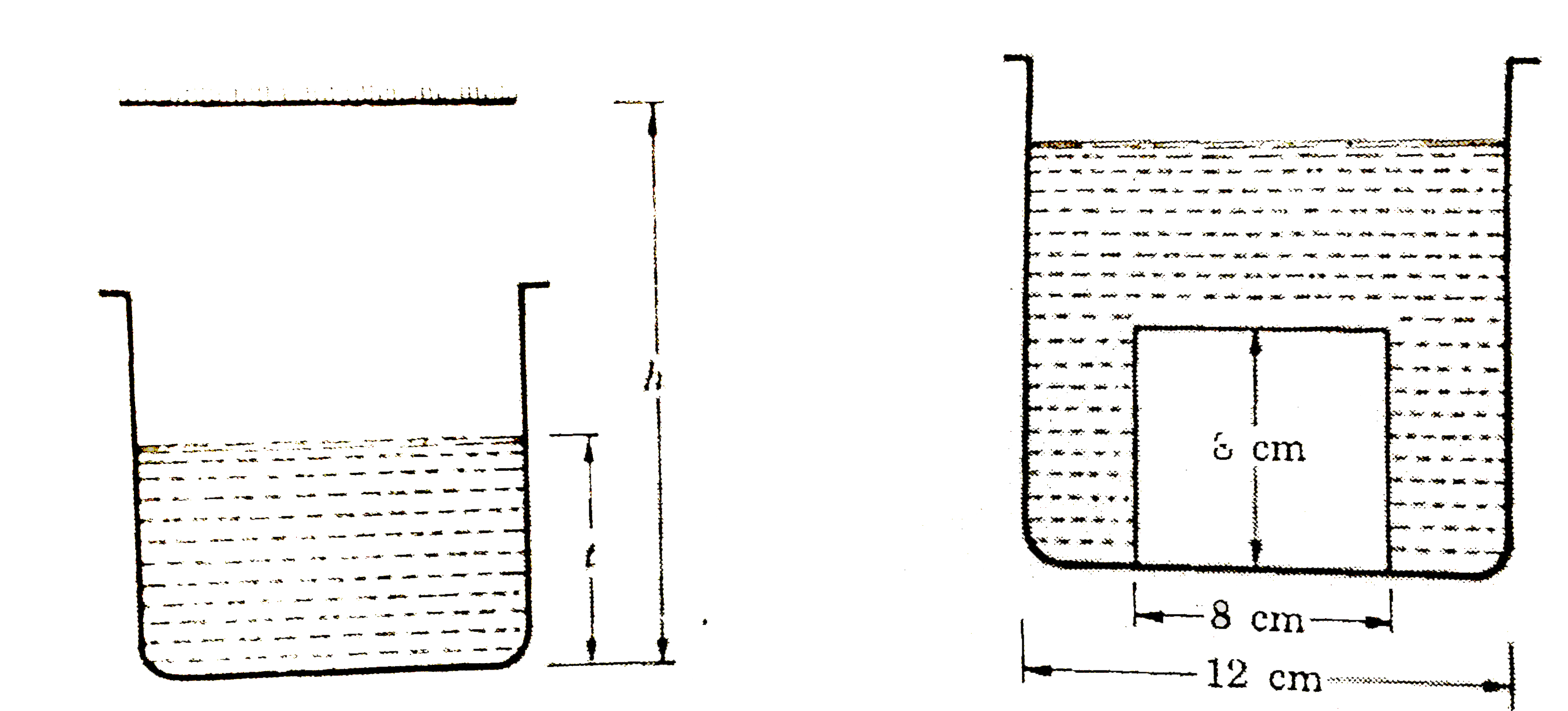 View Solution
View SolutionA fish is 60 cm under water (μ=4/3). A bird directly overhead looks at the fish. If the bird is at a distance of 120 cm from the water surface, (a) What is the apparent position of the fish as seen by the bird and (b) what is the apparent position of the bird as seen by the fish?
 View Solution
View Solution

