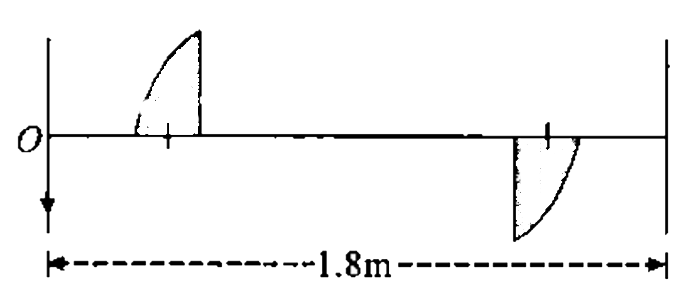
A thin plano-convex lens of focal length f is split into two halves. One of the halves is shifted along the optical axis as shown in figure. The separation between object and image planes is 1.8 m. The magnification of the image, formed by one of the ball lens is 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.

The correct Answer is:D
For both the halves, position of object and image is same. Only difference is of
magnification. Magnification for one of the halves is given as 2(>1). Thus can be for the first
one, because for this, |v|>|u|. Therefore, magnification, |m|=|v/u|>1.
So, for the first half
|v/u|=2
|v|=2|u|
or Let u=−x,
then v=+2x
and |u|+|v|=1.8m
i.e. 3x=1.8m
or x=0.6m
Hence, u=−0.6m
and v=+1.2m
using 1f=1v−1u=11.2−1−0.6=10.4
∴f=0.4m
For the second half, 1f=11.2−d−1−(0.6+d)
or 10.4=11.2−d−1−(0.6+d)
Solving this, we get d=0.6m
Magnification for the second half will be
m2=vu=0.6−(1.2)=−12
and magnification for the first half is
m2=vu=1.2−(0.6)=−2
the ray diagram is as follows:

Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Solved Example15videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.13videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 101videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
A thin plano-convex lens.of focal length f is split into two halves : One of the halves is shifted along the optical axis (figure)The separation between object and image planes is 1.8m.The magnification of the image formed by one of the half lensis 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.
 View Solution
View SolutionA thin plano-convex lens of focal length f is split into two halves. One of the halves is shifted along the optical axis as shown in figure. The separation between object and image planes is 1.8 m. The magnification of the image, formed by one of the ball lens is 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
AThe focal length of each half becomesf2BThe focal length of each half becomes 2fCThe focal length of each half remains fDThe focal length of each half becomes f4 - Question 2 - Select One
The distance between an object and its real image formed by a lens is D. If the magnification is m, the focal length of the lens is
A(m−1)DmBmD(m+1)C(m−1)Dm2DmD(m+1)2 - Question 3 - Select One
Shown an object and its image formed by a thin lens. Then the nature and focal length of lens is
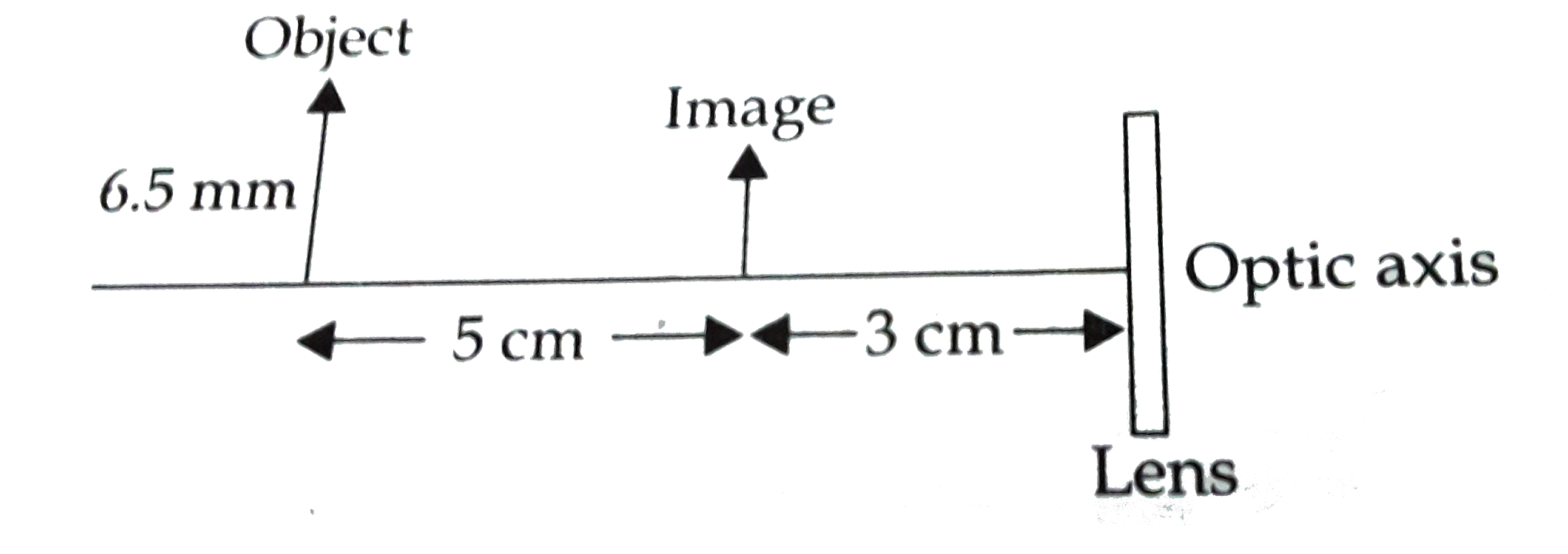 Af=4.8cm converging lensBf=−4.8cm diverging lensCf=2.18cm converging lensDf=−2.18cm diverging lens
Af=4.8cm converging lensBf=−4.8cm diverging lensCf=2.18cm converging lensDf=−2.18cm diverging lens
A thin plano-convex lens of focal length f is split into two halves. One of the halves is shifted along the optical axis as shown in figure. The separation between object and image planes is 1.8 m. The magnification of the image, formed by one of the ball lens is 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.
 View Solution
View SolutionA thin double convex lens of focal length f is broken into two equal halves at the axis. The two halves are combined as shown in figure. What is the focal length of combination in (ii) and (iii).
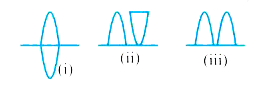 View Solution
View SolutionThe distance between the object and the real image formed by a convex lens is d. If the linear magnification is m, find the focal length of the lens in terms of d and m.
View SolutionDraw ray diagram showing the image formation by a convex lens when an object is placed at twice the focal length of the lens.
View SolutionA cocave lens forms the image of an object such that the distance between the object and image is 10 cm and the magnification produced is 1/4. the focal length of the lens will be
View Solution
