An equilateral glass prism of refractive index 1.5 is immersed in water. Find the angle of deviation produced when a ray of light is incident at 42∘ on one face of the prism.
(Refractive index of water = 1.33)
Angle of prism, A=60∘ (equilateral prism)
Refractive index of glass, μg=1.5
Refractive index of water, μw=1.33
∴ Refractive index of glass w.r.t. water is
wμg=μgμw/(1.33)
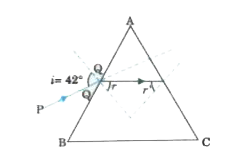
For refraction at face AB:
Angle of incidence, i=42∘
Angle of refraction, r=?
Now, wμg=sinisinr
⇒ 1.51.33=sin42∘sinr
⇒ sinr=sin42∘×1.331.5
=0.6691×1.331.5
=0.59
⇒ r=36.16∘
For refraction at face AC:
Angle of refraction at face AC, r.=?
We know that, r+r.=A
r.=A−r=60∘−36.16∘
=23.84∘
Let e be the angle of emergence, then
wμg=sinesinr.
⇒ sine=wμg×sinr.
=1.51.33×0.4041
=0.4556
⇒ e=27∘
Angle of deviation will be
δ=i+e−A=42∘+27∘−60∘
=9∘
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (1)13videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (2)9videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
An equilateral glass prism (μ−1.6) is immersed in water (μ=1.33). Calculate the angle of deviation produced for a ray of light incident at 40∘ on one face of the prism.
View SolutionAn equilateral glass prism is made of a material of refractive index 1.500. Find its angle of minimum deviation.
View Solution
Knowledge Check
- Question 1 - Select One
When a ray of light is incident normally on one refracting surface of an equilateral prism of refractive index 1.5, then
Athe ray undergoes total internal reflection at the second refracting surface of prismBemergent ray is deviated by 30∘Cemergent ray is deviated by 60∘Demergent ray just grazes the second refracting surface of the prism - Question 2 - Select One
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if
 Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these
Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these - Question 3 - Select One
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if.
 Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
An equilateral glass prism has a refractive index 1.6 in air. Calculate the angle of minimum deviation of the prism, when kept in a medium of refractive index 4√2/5
View SolutionA prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionChoose the most appropriate option.
A glass prism ABC (refractive index 1.5), immersed in water (refractive index 4/3). A ray of light is incidentally normally on face AB. If it is totally reflected at face AC, then
 View Solution
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, Fig. if :
 .View Solution
.View Solution
