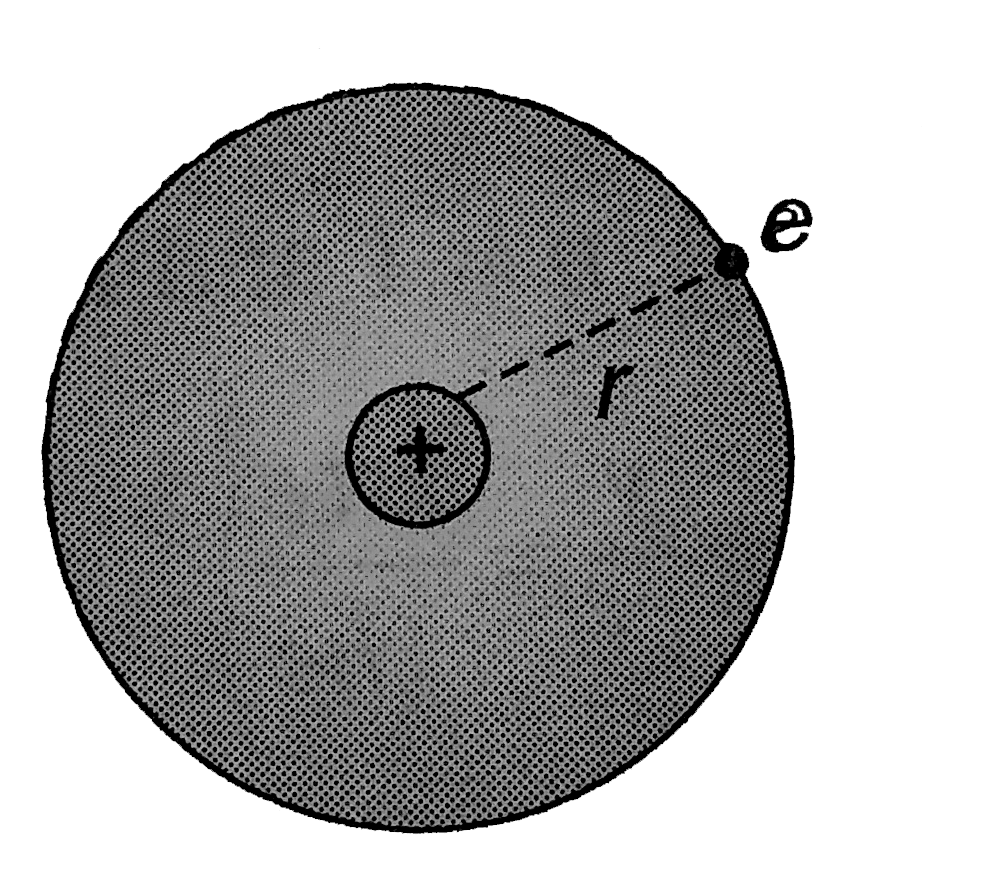
If m is mass of electron, v its velocity, r the radius of stationary circular orbit around a nucleus with charge Ze, then from Bohr's first postulate, the kinetic energy k=12mv2 of the electron is
12Ze2r
12Ze2r2
Ze2r
Zer2
The correct Answer is:A
In the revolution of electron, coulomb force provides the necessary centripetal force
⇒ze2r2=mv2r⇒mv2=ze2r
∴K.E.12mv2=ze22r
Related Playlists
- BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Atomic Spectrum53videos
ATOMIC PHYSICS
- BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Problems Based On Mixed Concepts43videos
ATOMIC PHYSICS
- BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test30videos
ATOMIC PHYSICS
- BOOK - A2ZCHAPTER - ALTERNATING CURRENTEXERCISE - Section D - Chapter End Test30videos
ALTERNATING CURRENT
- BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section D - Chapter End Test29videos
CURRENT ELECTRICITY
Knowledge Check
- Question 1 - Select One
The time of revolution of an electron around a nucleus of charge Ze in nth Bohr orbit is directly proportional to
AnBn3Z2Cn2ZDZn - Question 1 - Select One
An electron of charge 'e' is revolving in a circular orbit of radius r around a nucleus with speed v. The equivalent current is
A2eπrvBe vrCev2πrDzero - Question 1 - Select One
An electron of mass m and charge -e moves in circular orbit of radius r round the nucleus of charge +Ze in unielectron system. In CGS system the potential energy of electron is
A+Ze2r2B−Ze2rCZe22rD−Ze22r - Question 1 - Select One
An electron revolve round the nucleous with the radius of the circular orbit is 'r' . To double the kinetic energy of the electron its orbital radius will be
Av/√2B√2rC2rDr/2 - Question 1 - Select One
An electron of charge e is moving in a circular orbit of radius r around a nucleus, at a frequency v. The magnetic moment associated with the orbital motion of the electron is
A2πver2Bπvr22Cπevr2Dπvr24 - Question 1 - Select One
An electron of charge e moves in a circular orbit of radius r round a nucleus the magnetic field due to orbit motion off the electron at the site of the nucleus is B. The angular velocity ω of the electron is
Aω=μ0eB4πrBω=μ0eBπrCω=4πrBμ0eDω=2πrBμ0e - Question 1 - Select One
When an electron of charge , e and mass , m moves with velocity v around the nuclear charge 'Ze' describing the circular orbit, the potential energy of the electron is
AZe2/rB−Ze2/rCZe2/r2Dmv2/r
Similar Questions
An electron rotates in a circle around a nucleus with positive charge Ze. How is the electrons'velocity realted to the radius of its orbit?
View SolutionA particle of charge equal to that of electron and mass 208 times the mass of the electron moves in a circular orbit around a nucleus of charge +3e. Assuming that the Bohr model of the atom is applicable to this system find the value of n for which the radius of the orbit is approximately the same as that of the first Bohr orbit of the hydrogen atom.
View SolutionA particle known as mu mean has a charge equal to that of no electron and mass 208times the mass of the electron B moves in a circular orbit around a nucleus of charge +3e Take the mass of the nucles to be infinite Assuming that the bohr's model is applicable to this system (a)drive an eqression for the radius of the nth Bohr orbit (b) find the value of a for which the redius of the orbit it approninately the same as that at the first bohr for a hydrogen atom (c) find the wavelength of the radiation emitted when the u - mean jump from the orbit to the first orbit
View Solution

