Two magnets of same size and mass make respectively 10 and 15 oscillations per minute at certain place. The ratio of their magnetic moment is
4:9
9:4
2:3
3:2
The correct Answer is:A
T=2π√1MBH⇒T1T2=√M2M1
⇒M1M2=T22T21=(60/15)2(60/10)2=49
Related Playlists
- BOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Magnetic Materials50videos
MAGNETISM AND MATTER
- BOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Problems Based On Mixed Concepts37videos
MAGNETISM AND MATTER
- BOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test30videos
MAGNETISM AND MATTER
- BOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section D - Chapter End Test30videos
GEOMETRICAL OPTICS
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Mock Test 344videos
MOCK TEST
Similar Practice Problems
- Question 1 - Select One
Two magnets are held together in a vibration magnetometer and are allowed to oscillate in the earth's magnetic field with like poles together, 12 oscillations per minute are made but for unlike poles together only 4 oscillations per minute are executed. The ratio of their magnetic moments is
A3:1B1:3C3:5D5:4 - Question 1 - Select One
Two magnets are held together in a vibration magnetometer and are allowed to oscillate in the earth's magnetic field with like poles togather, 12 oscillations per minute are made but for unlike poles togather only 4 oscillations per minute are axecuted. The ratio of their magnetic miments is
A3:1B1:3C3:5D5:4 - Question 1 - Select One
Two bar magnets are placed in vibration magnetometer and allowed to vibrate. They make 20 oscillations per minute when their similar pole are on the same side, while they make 15 osicillations per minute when their opposite poles lie on the same side. The ratio of their magnetic moments is
A7:25B25:7C25:16D16:25 - Question 1 - Select One
Read the following passage on the basis of your understanding of the following paragraph and the related studied concepts:
A freely suspended bar magnet capable of rotation in a horizontal plane in its equilibrium state, rests in the direction of earth's magnetic field at the place. If the magnet is slightly rotated from its equilibrium direction and then released, it executes angular oscillations of period T given as per relation
T=2π√ImBH
Here I moment of inertia of bar magnet about its oscillation axis, magnetic moment of bar magnet and BH horizontal component of earth's magnetic field at the place.
An oscillation magnetometer is designed on this principle and is employed to compare magnetic moments of magnets and for determining earth's magnetic field at a place.
Two bar magnets A and B of same configuration and mass have oscillation periods of 2s and 2.5 s respectively at a given place. The ratio of magnetic moments of A and B isA5:4B√5:2C25:16D16:25 - Question 1 - Select One
Read the following passage on the basis of your understanding of the following paragraph and the related studied concepts:
A freely suspended bar magnet capable of rotation in a horizontal plane in its equilibrium state, rests in the direction of earth's magnetic field at the place. If the magnet is slightly rotated from its equilibrium direction and then released, it executes angular oscillations of period T given as per relation
T=2π√ImBH
Here I moment of inertia of bar magnet about its oscillation axis, magnetic moment of bar magnet and BH horizontal component of earth's magnetic field at the place.
An oscillation magnetometer is designed on this principle and is employed to compare magnetic moments of magnets and for determining earth's magnetic field at a place.
Two bar magnets of same dimensions and same mass but different magnetic moments are placed together in an oscillation magnetometer with their like poles together and the combination completes 20 oscillations per minute. Subsequently, the two magnets are placed with their unlike poles together in the oscillation magnetometer. Now the combination completes 10 oscillations per minute only. Compare the ratio of magnetic moments of two given magnets.A53B21C41D12 - Question 1 - Select One
A magnet freely suspended in a vibration magnetometer makes 10 oscillations per minute at a place A and 20 oscillations per minute at a place B. If the horizontal component of earth's magnetic field at A is 36×10−6T, then its value at B is
A36×10−6TB72×10−6TC144×10−6TD288×10−6T - Question 1 - Select One
Calculate the angle of dip, if a dip needle oscillating in a vertical plane makes 40 oscillations per minute in a magnetic meridian and 30 oscillations per minute in a vertical plane at right angle to the magnetic meridian.
Aθ=tan−1(0.5625)Bθ=tan−1(0.325)Cθ=tan−1(0.425)Dθ=tan−1(0.235) - Question 1 - Select One
The angle of dip if dip needleoscillating in vertical plane makes 40 oscillations per min in a magnetic meridian and 30 oscillations per minute in vertical plane at right angle to the magnetic meridian is
Aθ=sin−1(0.5625)Bθ=sin−1(0.325)Cθ=sin−1(0.425)Dθ=sin−1(0.235)
Similar Questions
The combination of two bar magnets makes 20 oscillations per minute in an oscillation magnetometer when like poles are tied together and 5 oscillations per minute when unlike poles are kept together. Then ratio of the magnetic moment of magnets is
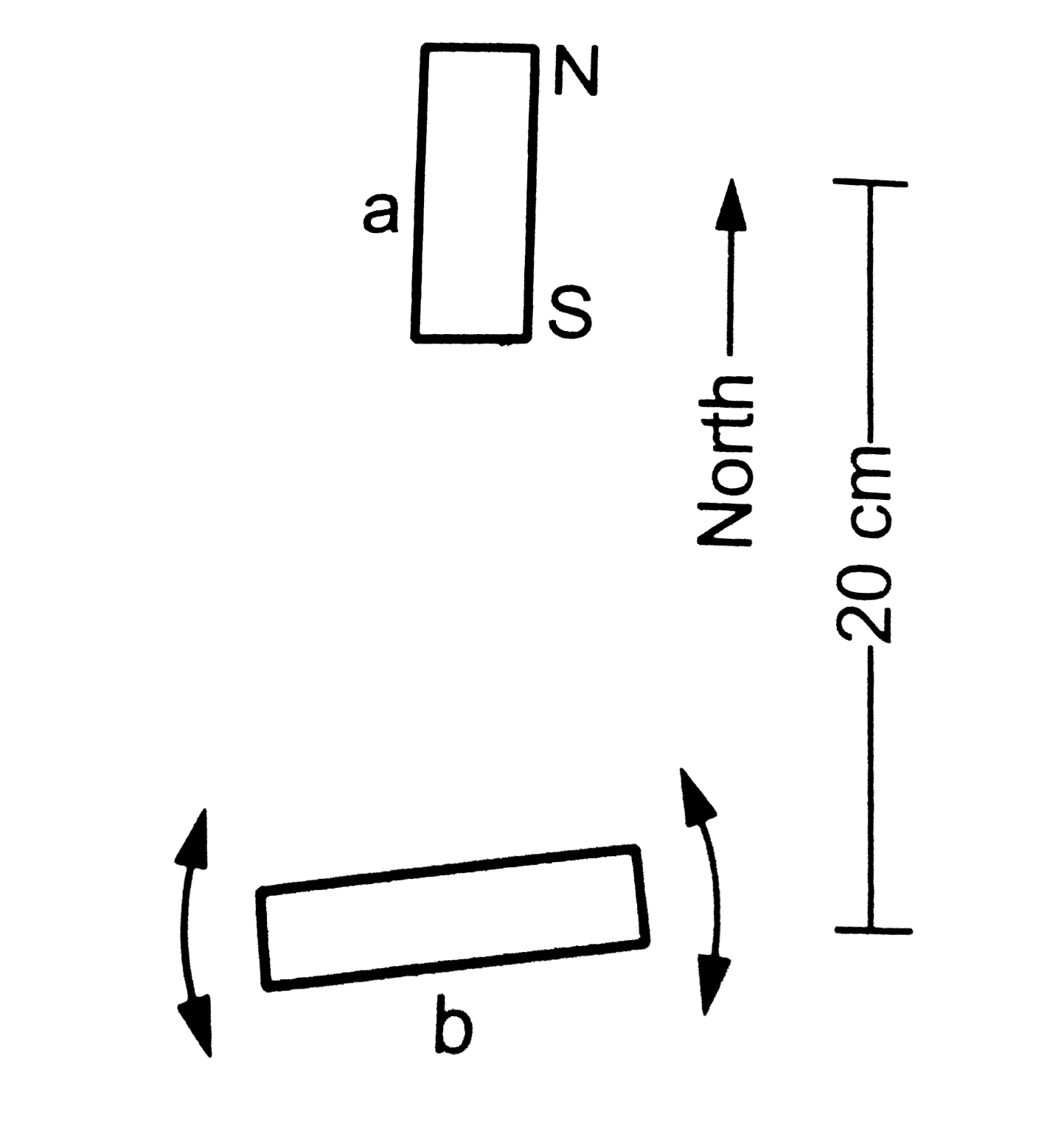
View SolutionThe frequency of oscillation of the magnet in an oscillation magnetometer in the earth's magnetic field is 40 oscillations per minute. A short bar magnet is placed to the north of the magnetometer, at a separation of 20cm from the oscillating magnet, with its north pole pointing towards north (figure). The frequency of oscillation is found to increase to 60 oscillations per minute. Calculate the magnetic moment of this short bar magnet. Horizonatl component of the earth's magnetic field is 24μT.
 View Solution
View Solution

