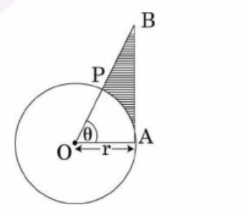
Fig. 15.17, shows a sector of a circle, centre O , containing an angle θo , prove that: (FIGURE) (i) Perimeter of the shaded region is r (tanθ+secθ+πθ180−1) (ii) Area of the shaded region is r22 (tanθ−πθ180)
Step by step video & image solution for Fig. 15.17, shows a sector of a circle, centre O , containing an angle thetao , prove that: (FIGURE) (i) Perimeter of the shaded region is r\ (tantheta+sectheta+(pitheta)/(180)-1) (ii) Area of the shaded region is (r^2)/2\ (tantheta-(pitheta)/(180)) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Knowledge Check
- Question 1 - Select One
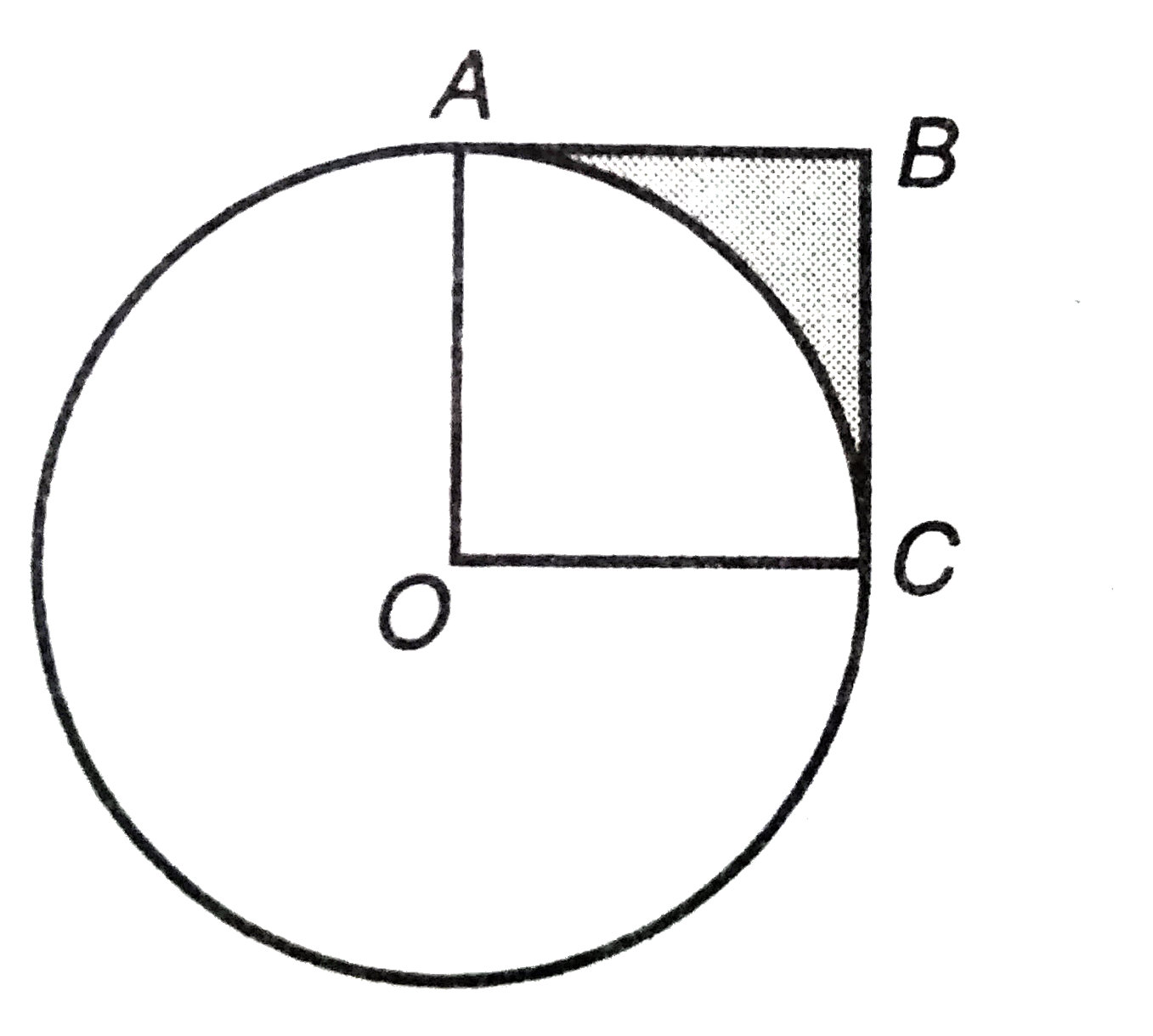
In the figure above, OABC is a square. If the area of circle O is 2π, what is the area of the shaded region?Aπ2−1B2−π2Cπ−2Dπ−12 - Question 1 - Select One

In the figure above, Radius of circle is 8 and angle formed by sector at center is 120∘ , what is the area of the shaded region ?A16π3−16√3B16π3−16C16π3−64√3D64π3−16√3
Similar Questions
Figure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionIn the given figure, is shown a sector OAP of a circle with centre 0, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ+secθ+πθ180−1]
 View Solution
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn figure, three sectors of a circle of radius 7 cm, making angles of 60∘,80∘ and 40∘ at the center are shaded. Find the area of the shaded region.
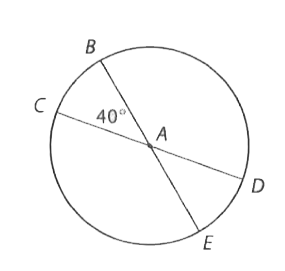
View SolutionBE and CD are both diameters of circle with centre A (see figure). If the area of the circle is 180units2, what is the total area of the shaded regions?
 View Solution
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.
 View Solution
View SolutionIn Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.View SolutionIn figure arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region .
 View Solution
View Solution

