Find graphically the solution sets of each of the following systems of inequalities :
x1+x2≤6
x1≥3
2x1+3x2≥3
x1≥0,x2≥0
Step by step video & image solution for Find graphically the solution sets of each of the following systems of inequalities : x_(1) + x_(2) le 6 x_(1) ge 3 2x_(1) + 3x_(2) ge 3 x_(1) ge 0, x_(2) ge 0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Fill in the blanks9videos
LINEAR PROGRAMMING
- BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Question2videos
LINEAR PROGRAMMING
- BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Self Assessment Test8videos
LINEAR PROGRAMMING
- BOOK - ML KHANNACHAPTER - LIMITS, CONTINUITY AND DIFFERENTIABILITY EXERCISE - MISCELLANEOUS EXERCISE (ASSERTION/ REASONS)3videos
LIMITS, CONTINUITY AND DIFFERENTIABILITY
- BOOK - ML KHANNACHAPTER - LOGARITHMS AND SURDSEXERCISE - Miscellaneous exercise3videos
LOGARITHMS AND SURDS
Similar Questions
A mathematical technique for finding the optimal use to an organization's scarce resources is called ………… .
09:22View SolutionA whole-sale dealer deals in two kinds, A and B say, of mixture of nuts. Each kg of mixture A contains 60 gms of almonds, 30 gms of cashew nuts, and 30 gms of hazel nuts. Each kg of mixture B contains 30 gms of almonds, 60 gms of cashew nuts, and 180 gms of hazel nuts. The remainder of both mixtures is pea nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 gms of almonds, 300 gms of cashew nuts, and 540 gms of hazel nuts. Mixture A costs Rs. 8 per kg. And mixture B costs Rs. 12.00 per kg. Assuming that mixture A and V are uniform :
How many kgs of each should he use to minimize the cost of the bag ?View SolutionMaximum value of Z = 12x + 3y subject to constraints x≥0,y≥0,x+y≤5 and 3x+y≤9 is
View SolutionLet f(x)=(x+1)2−1,x≥−1 , IF f(x):[−1,∞]→[−1,∞]
Statement 1: The set {x:f(x)=f−1(x)}={0,−1}
Statement-2: f is a bijection.07:22View Solution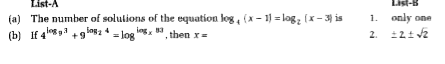
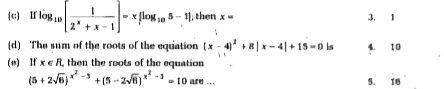 03:06View Solution
03:06View SolutionBy graphical method, the solutions of linear programming problem maximise Z=3x1+5x2 subject to constraints 3x1+2x2≤18,x1≤4,x2≤6x1≥0,x2≥0 are
05:02View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
निम्नतम z=2x1+3x2
प्रतिबंध x1+x2≤4
6x1+2x2≥8
x1+5x2≥8
x1+5x2≥4
x1≤3
x2≤3
तथा x1,x2≥003:39View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
अधिकतम z=3x1+2x2
प्रतिबंध x1+x2≥1
x2≡5x1≤0
5x2−x1≥0
x1−x2≤6
x1≤3
तथा x1≥0.x2≥0View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
अधिकतम z=3x1+2x2
प्रतिबंध 2x1+x2≤11/3
x1≤2
x1+x2≤3
तथा x1,x2≥005:05View SolutionFor L.P.P. maximize z=4x1+2X2 subject to 3x1+2x2≥9,x1−x2≤3,x1≥0,x2≥0 has ……
06:02View Solutionरेखीय प्रक्रमन समस्या Min z=−x1+2x2 जबकि −x1+3x2≤0,x1+x2≤6,x1−x2≤2 तथा x1,x2≥0 के लिए x1 का मान है
03:25View Solutionउद्धेश्य फलन z=x1+x2 के व्यवरोध x1+x2≤1,3x1+x2≥3 तथा x1,x2≥0 के लिए होंगे
10:42View Solutionअसमिकाओं x1+x2≤3,2x1+5x2≥10,x1≥0,x2≥0के व्यापक हल में स्थित बिंदु होगा -
07:31View SolutionThe solution of linear programming problem, maximize Z=3x1+5x2 subject to 3x1+2x2≤18,x1≤4,x2≤6,x1≥0,x2≥0 is ………..
04:03View SolutionBy graphical method, the solutions of linear programming problem maximise Z=3x_(1)+5x_(2) subject to constraints 3x_(1)+2x_(2) le 18, x_(1) le 4, x_(2) le 6, x_(1) ge0,x_(2) ge 0 are
04:10View Solution

