Find the values of x∈[0,2π] for which function f(x)=tan−1(tanx)andg(x)=cos−1(cosx) are identical
The correct Answer is:[0,π/2)∪{2π]
Let us draw the graph of both th efunction for x∈[0,2π]
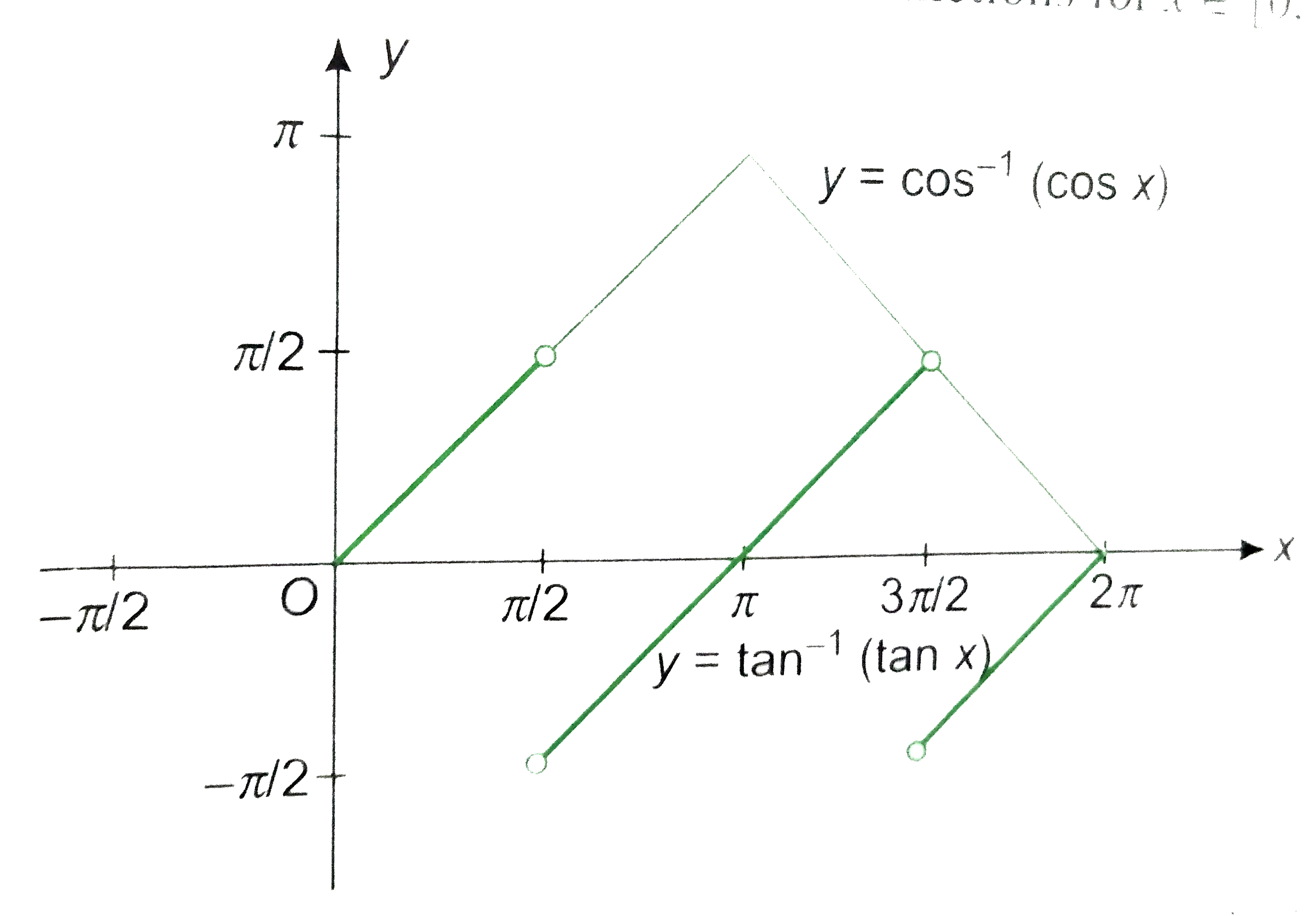
In the above figure, graph of y=f(x)andy=g(x) coincide for x∈[0,π/2)∪{2π}
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.312videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.412videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.112videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE3videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
Find the value of x for which function are identical. f(x)=tan−1x+tan−1(1x)andg(x)=sin−1x+cos−1x
View SolutionFind the value of x for which function are identical. f(x)=xandg(x)=11/x
View SolutionThe domain set of the function
f(x)=tan−1x−cot−1x+cos−1(2−x) isView SolutionFind the set of values of x for which tan3x−tan2x1+tan3xtan2x = 1
View Solution2tan−1(cosx)=tan−1(2cosecx)
View SolutionFind the value of x for which function are identical. f(x)=cosxandg(x)=1√1+tan2x
View SolutionFind the range of f(x)=sin−1x+tan−1x+cos−1x
View SolutionFind the value of x for which function are identical. f(x)=cosxandg(x)=1√1+tan2x
View SolutionIf the function f(x)=sin−1x+cos−1x and g(x) are identical, then g(x) can be equal to
View SolutionFind the set of values of x for which tan3x−tan2x1+tan3x.tan2x=1.
View Solution

