Find which of the operations given above has identity.
(i) IN Q a * b a-b
Let a, b ∈ Q
∴ a*b =a - b ∈ b - a ∈ b*a
⇒ Operation * is not commutatve.
∴ a*(b*c) = a-(b-c)
=a-b + c
and (a*b) * c = (a-b) *c
= a-b-c
∴ a* (b*c) ≠ (a*b) * c
Therefore, operation * is not associative.
(ii) In Q a*b =a2+b2
Let a,b ∈ Q
∴ a* b =a2+b2
=b2+a2= b*a
⇒ Operation * is commutative.
Let a,b,c ∈ Q
∴ a*(b*c) = a*(b2+c2)
=a2+(b2+c2)2
and (a*b)*c=(a2+b2)*c
=(a2+b2)+c2
∴ a* (b*c) ∈ (a*b) *c
⇒ Operation * is not associative.
(iii) In Q , a* b = a+ ab
Let a, b ∈ Q
∴ a* b = a+ ab and b* a = b+ba
Therefore, a*b ≠ b*a
⇒ Operation * is not commutative
Let a,b,c ∈ Q
∴ a*(b*c) = a* (b+ bc)
= a+a(b +bc)= a+ ab + abc
and (a*b) * c = (a+ab) *c
=a+ ab + ac + abc
∴ a* (b*c) ≠ (a * b) * c
⇒ OPeration * is not associative .
(iv) In Q, a* b =(a−b)2
∴ a* b =(a−b)2
=(b−a)2= b * a
⇒ Operation * is commutative .
Let a,b,c ∈ Q
∴ a* (b*c) = a* (b−c)2
=[a−(b−c)2]2
and (a*b) *c =(a−b)2* c
=[(a−b)2−c]2
∴a*(b*c)≠(a * b)*c
⇒ Operatin * is not associative .
(v) In Q, a * b=ab4
Let a,b∈Q
∴ a * ( b*c) = a* (bc4)=a(bc4)4
(ab4)c4=(abc)*c=(a*b)*c
⇒ Operation * is associtative.(iv) In Q, a * b =ab2
Let a,b,c ∈ Q
∴ a* (b*c) =a*(bc)2
=a(bc)2=aab2c2
and (a*b) *c =(ab)2*c=ab2c2
∴ a* b (b*c) ≠ (a*b) *c
⇒ operation * is not associative .
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise19videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Exercise 1.314videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise19videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Miscellaneous Exercise23videos
THREE-DIMENSIONAL GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
Operators with higher precedence are evaluated before operators with relatively lower precedence. Arrange the operators given below in order of higher precedence to lower precedence.
(i) && (ii) % (iii) ≥ (iv) ++A(iv), (i), (iii), (ii)B(iv), (iii), (ii), (i)C(iv), (ii), (iii), (i)D(i), (ii), (iii), (iv) - Question 2 - Select One
Operators with higher precedence are evaluated before operators with relatively lower precedence. Arrange the operators given below in order of higher precedence to lower precedence.
(i) &&
(ii) %
(iii) >=
(iv) ++A(iv), (i), (iii), (ii)B(iv), (iii), (ii), (i)C(iv), (ii), (iii), (i)D(i), (ii), (iii), (iv)
Let ∗ be a binary operation on the set Q of rational numbers as follows:
(i) a∗b=a−b (ii) a∗b=a2+b2
Find which of the binary operations are commutative and which are associativeView SolutionA binary operation on a set has always the identity element.
View Solution
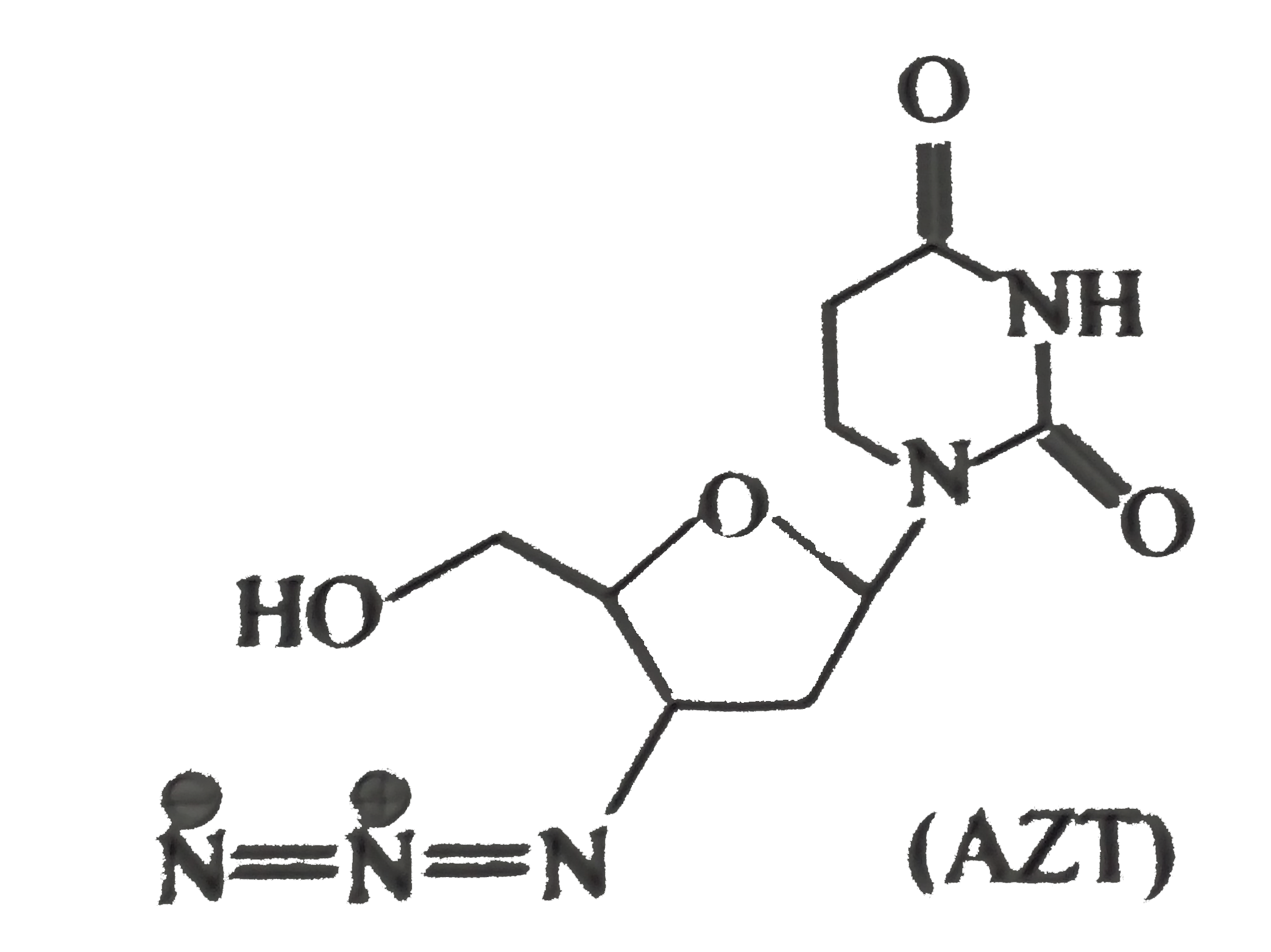
AZT structure is given above find which of the following functional groups are present in AZT.View SolutionGiven the circuit :
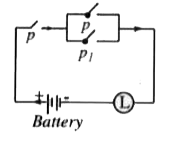
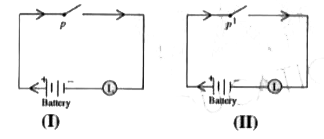
Which of the following is equivalent to the above circuit ?
The true statement in the above is/areView SolutionShow that zero is the identity for addition on R and 1 is the identity for multiplication on R. But there is no identity element for the operations −:R×R→Rand ÷:R⋅×R⋅→R⋅.
View SolutionFor the binary operation * on Z defined by a*b= a+b+1 the identity element is
View Solution

