If the points A (1,-2), B (2,3) , C (a,2) and D (-4-,3) form a parallelogram , them find the value of a and height of the parallelogram taking AB as base.
In parallelogram , we know that , diagonals are bisects each other i.e., mid - point of AC = mid - point of BD
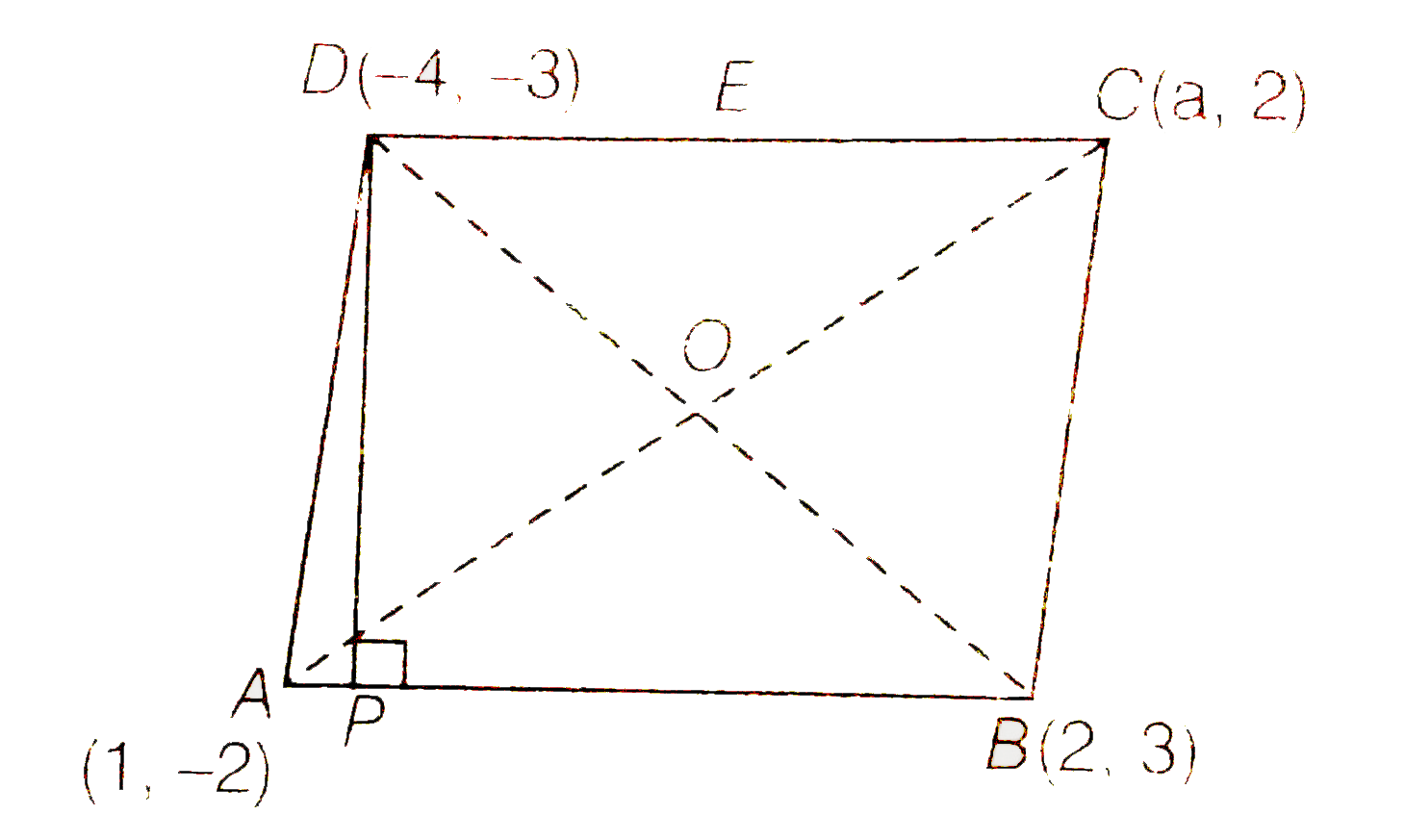
⇒(1+a2,−2+22)=(2−42,3−32) ⇒1+a2=2−42=−22=−1 [since , mid point of a line segment having points (x1,y(1))and(x2,y2) is (x1+x22,y1+y22)]
⇒1+a=−2
⇒a=−3
So , the required value of ais -3 .
Given thta , AB as base of a parallelogram and draw a perpendicular from D to AB which meet AB at P . So, DP is a height of a parallelogram.
Now , equation of base AB , passing throught the points (1,2) and (2,3) is
⇒(y−y1)=y2−y1x2−x1(x−x1)
⇒(y+2)=3+32−1(x−1)
⇒(y+2)=5(x−1)
⇒5x−y=7
Slope of AB, say m1=y2−y1x2−x1=3+22−1=5
Let the slope of DP be m2. Since , DP is perpendicular to AB. By condition of perpendicularity ,
m1⋅m2=−1⇒5⋅m2=−1
⇒m2=−15
Now , Eq . of having slope (−15) and passing the point (-4,-3) is
(y−y1)=m2(x−x1)
⇒(y+3)=−15(x+4)
⇒5y+15=−x−4
⇒x+5y=−19 ...(ii)
On adding Eqs. (i) and (ii) , then we get the intersection point P.
Put the value of from Eq. (i) in Eq.(ii) , we get
x+5(5x−7)=−19 [using Eq. (i)]
⇒x+25x−35=−19
⇒26x=16
∴x=813
Put the value of x in Eq . (i) we get
y=5(813)−7=4013−7
⇒y=40−9113⇒y=−5113
∴ coordinates of point P ≡(813,−5113)
So , length of the height of a para,,elogram ,
DP=√(813+4)2+(−5113+3)2
∵ by distance formula , distance between two points (x1,y1)and(x2,y2), is d=√(x2−x1)2+(y2−y1)2]
⇒DP=√(6013)2+(+1213)2
=113√3600+144
=113√3744=12√2613
Hence , the required length of height of a parallelogram is 12√2613
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 7.3 Very Short Answer Type Questions20videos
COORDINATE GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSEXERCISE - LONG ANSWER TYPES QUESTIONS18videos
INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS
Similar Practice Problems
- Question 1 - Select One
If the points A(−2,−1),B(1,0),C(a,3) and D(1,b) form a parallelogram ABCD, Then the values of a and b are
Aa=−4,b=−2Ba=−4,b=2Ca=4,b=2Da=2,b=−4
Similar Questions
If the points (−2, −1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y .
View SolutionOf A(−2,−1),B(a,0),C(4,b) and D(1,2) are the vertices of a parallelogram, find the values of a and b.
View SolutionIf A(−2,−1),B(a,0),C(4,b)andD(1,2) are the vertices f a parallelogram, find the values of aandb
View SolutionIf the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.
View SolutionIf the points A(1,3), B(−2,1), C(x,2) and D(−1,5) are given and AB is perpendicular to CD, find the value of x.
View SolutionIf the point (x,−1),(3,y),(−2,3),and(−3,−2) taken in order are the vertices of a parallelogram, then find the values of xandy.
View SolutionShow that the points (3, -1, 2), (5, -2, -3), (-2, 4, 1) and (-4, 5, 6) form a parallelogram.
[Hint : Opposite sides of parallelogram are equal.]View SolutionIf the points A(1, −2), B(2, 3), C(−3, 2) and D(−4, −3) are the vertices of parallelogram ABCD , then taking AB as the base, find the height of the parallelogram.
View SolutionIn Figure, ABCD is a parallelogram. Find the values of xandy.
View Solution

