In a LPP, the objective function is always ...........Solution in Punjabi
The correct Answer is:Linear
Step by step video, text & image solution for In a LPP, the objective function is always ........... by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-III : TRUE OR FALSE QUESTIONS)10videos
LINEAR PROGRAMMING
- BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 6 MARKS7videos
LINEAR PROGRAMMING
- BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-I : MULTIPLE CHOICE QUESTIONS)15videos
LINEAR PROGRAMMING
- BOOK - ACCURATE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS CARRYING 4 MARKS27videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - ACCURATE PUBLICATIONCHAPTER - MATRICESEXERCISE - QUESTIONS CARRYING 6 MARKS4videos
MATRICES
Similar Questions
If the feasible region for a linear programming problem is bounded, then the objective function Z = ax+by has both a maximum and a minimum value on R.
01:14View SolutionFind the maximum value of f = x+2 y subject to the constraints
2x+3y≤6
x+4y≤4
x,y≥001:11View SolutionThe feasible solution for a LPP is shown in Fig. Let. Z = 3x - 4 y be the objective function. Minimum of Z occurs at
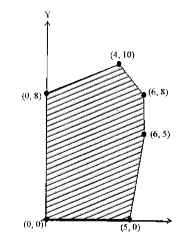 01:55View Solution
01:55View SolutionWrite the value of tan−1[2sin(2cos−1√32)].
01:03View SolutionIf A=⎡⎢⎣1−202130−21⎤⎥⎦,B=⎡⎢⎣72−6−21−3−425⎤⎥⎦ , find AB Also solve x−2y=10,2x+y+3z=8,−2y+z=7
01:21View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
02:19View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
01:37View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always finite.
02:11View SolutionObjective function of an LPP is
02:22View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?01:50View Solutionकिसी LPP में उद्देश्य फलन सदैव .... होता है |
01:36View Solutionकिसी LPP में, उद्देश्य फलन Z=ax+by का अधिकतम मान सदैव परिमित होता है |
02:08View SolutionThe objective function of an LPP is
02:20View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
01:44View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
01:14View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always finite.
01:30View Solution

