Let f:R→R:f(x)=(x+1) and g:R→R:g(x)=(x2−4). Write down the formulae for (fog).Solution in Tamil
f(x)=[x2−x−1],x∈[−1,2]
Let us first draw the graph of y=x2−x−1, which is an upward parabola having vertex at (1/2,-5/4).
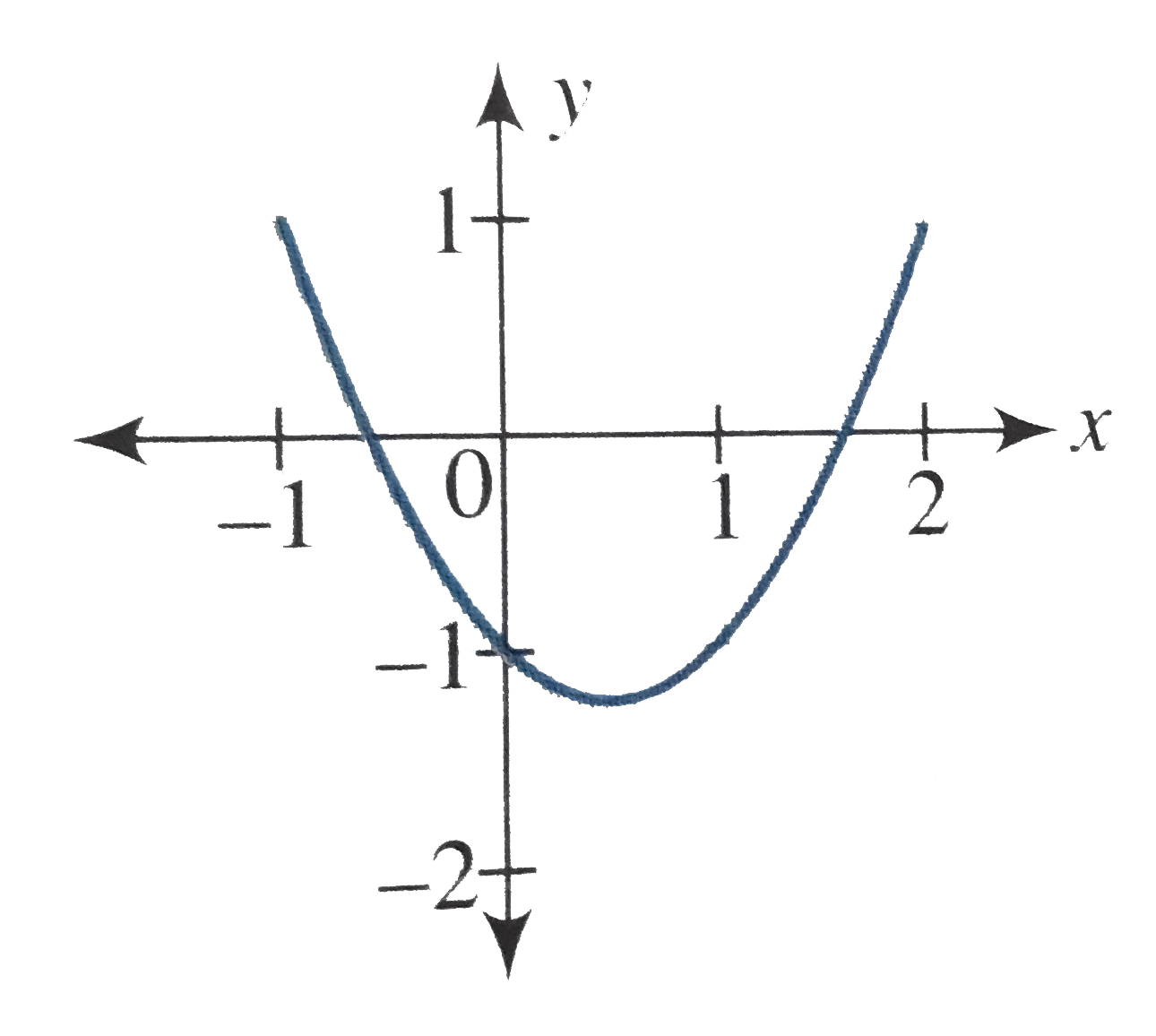
The graph of f(x)=[x2−x−1] can be drawn as shown in the following figure.
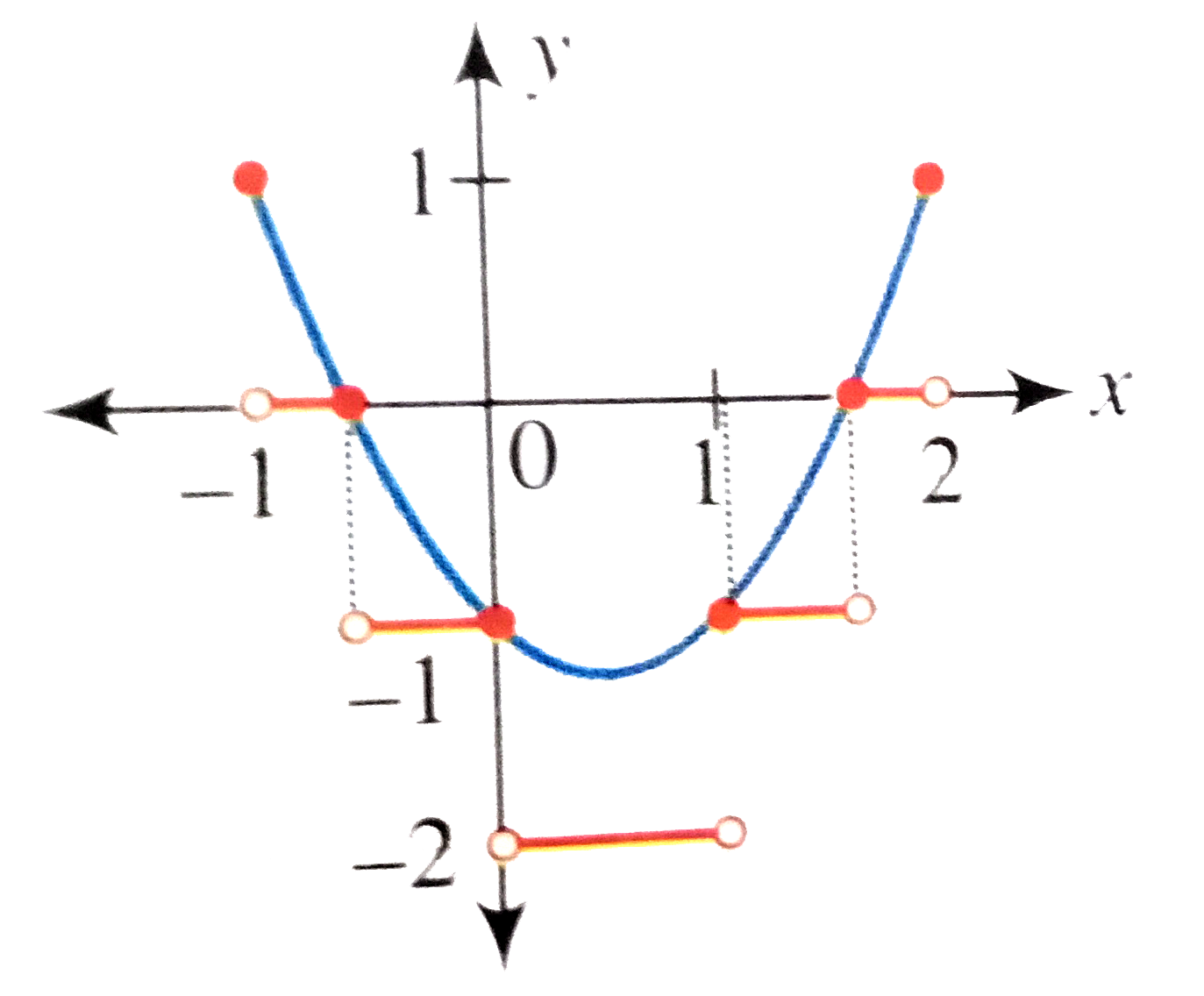
From the figure, y=f(x) is discontinuous at x=−1,0,2andthevaluesofxforwhichx^(2)-x-1=0orx=(1pmsqrt5)/(2).
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise14videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
02:56View SolutionDraw the graph of y=tan−1x+cot−1x
01:46View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=002:23View SolutionLet f:R→R and g:R→R be defined by f(x)=x2 and g(x)=x+1. Show that fog≠gof.
03:03View SolutionLet f:R→ and g: RvecRbedef∈ed+1andg(x)=x−1. Show that fog=gof=IR.
00:59View SolutionLet f:R rarr R:f(x)=8x^(3) and g:R rarr R;g(x)=x^((1)/(3)). Find (gof) and (fog) and show,that gof!= fog.
01:28View SolutionLet f:R rarr R:f(x)=x^(2),g:R rarr R:g(x)=tan x and h:R rarr R:h(x)=log x* Find a formula for ho(gof).Show that [ho(gof)]sqrt((pi)/(4))=0
02:00View SolutionLet R be the set of real numbers. If f:R→R:f(x)=x2 and g:R→R;g(x)=2x+1. Then, find fog and gof . Also, show that fog≠gof.
01:49View SolutionThe composite mapping fog of the maps f:R→R,f(x)=sinxandg:R→R,g(x)=x2, is
02:54View SolutionIf f:R→R,g:R→R are defined by f(x)=x2+2x−3,g(x)=3x−4, then (fog)(−1)=
01:50View SolutionIf f:R→R,g:R→R are defined by f(x)=3x−2,g(x)=x2+1, then (fog)(x2+1)=
02:12View Solutionयदि फलन f:R→R,f(x)=x2+2 और g:R→R,g(x)=xx−1 द्वारा परिभाषित हो , तो fog और gof ज्ञात कीजिए ।
02:16View Solutionf:R→R , और g:R→R इस प्रकार परिभाषित हैं : f(x)=1+x2 और g(x)=log x , तो (fog ) (x) और (fog) (x) ज्ञात कीजिए।
01:45View SolutionThe composite mapping fog of the maps f:R→R,f(x)=sinxandg:R→R,g(x)=x2, is
02:21View SolutionThe composite mapping fog of the maps f:R→R,f(x)=sinxandg:R→R,g(x)=x2, is
02:08View Solution

