Let S= set of point inside the square, T= set of points inside the triangles and C= the set of point inside the circle, if the triangle and circle intersect each other are contained in the square, then
S∩T∩C=ϕ
S∪T∪C=C
S∪T∪C=S
S∪T=S∩C
The correct Answer is:C
The given sets can be represented in Venn diagram as shown below
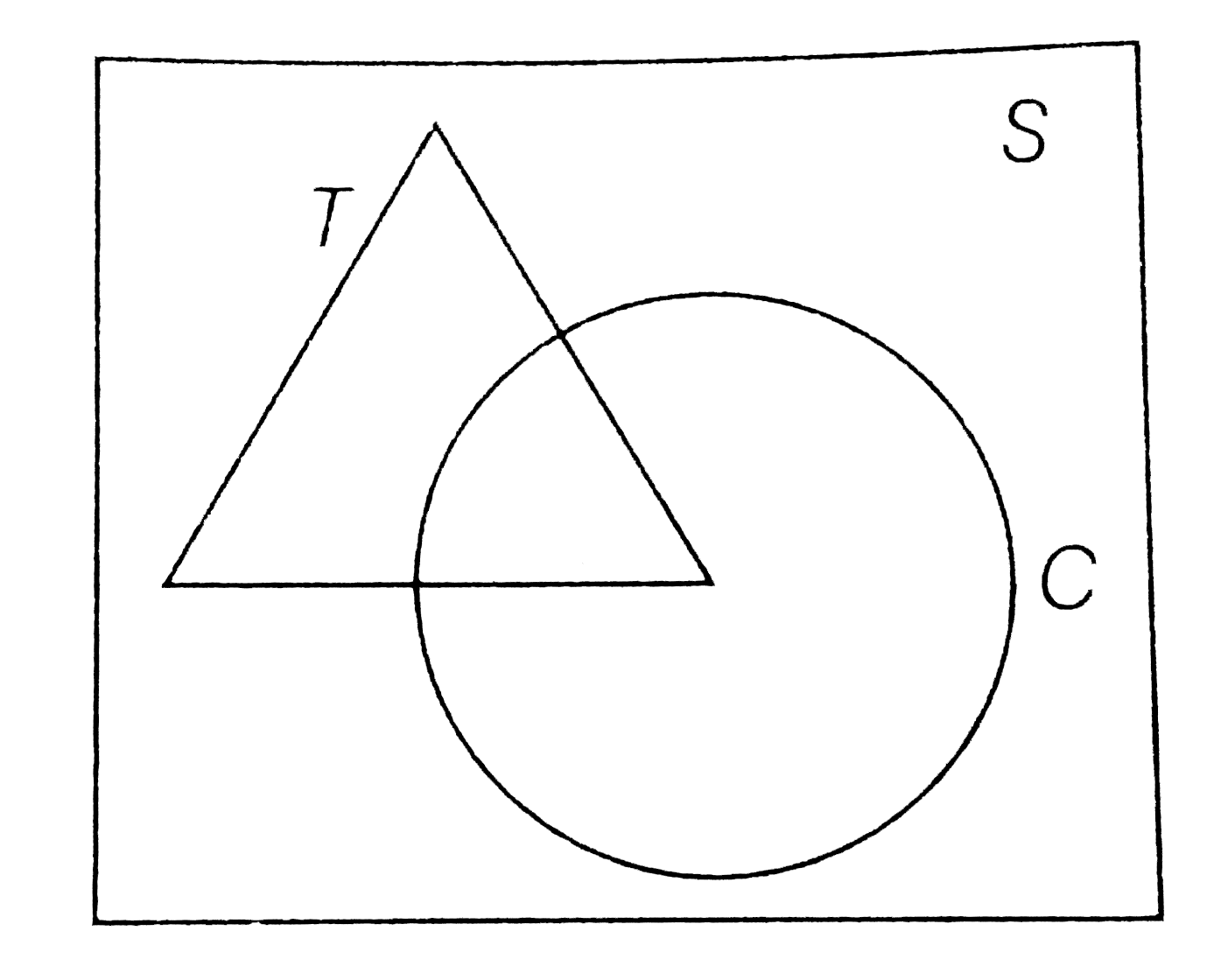
It is clear from the diagram that, S∪T∪C=S.
Related Playlists
- BOOK - NCERT EXEMPLARCHAPTER - SETSEXERCISE - FILLERS9videos
SETS
- BOOK - NCERT EXEMPLARCHAPTER - SETSEXERCISE - TRUE AND FALSE6videos
SETS
- BOOK - NCERT EXEMPLARCHAPTER - SETSEXERCISE - LONG ANSWERS TYPE QUESTIONS6videos
SETS
- BOOK - NCERT EXEMPLARCHAPTER - SEQUENCE AND SERIESEXERCISE - Match the comumms2videos
SEQUENCE AND SERIES
- BOOK - NCERT EXEMPLARCHAPTER - STATISTICSEXERCISE - FILLERS7videos
STATISTICS
Similar Practice Problems
- Question 1 - Select One
Number of tangents drawn from a point inside the circle is :
A1B2C4D0 - Question 1 - Select One
A point P lying inside a triangle is equidistant from the vertices of the triangle. Then the triangle has P as its
ACentroidBIncentreCOrthocentreDCircumcentre - Question 1 - Select One
If the point inside a triangle are equidistant from the vertex of the same triangle, what the name of that point is ?
AIncentreBOrthocentreCMedianDCircumcentre - Question 1 - Select One
The centre of the circle is at the origin and its radius is 10. Which of the following points lies inside the circle?
A(6,8)B(0, 11)C(-10,0)D(7,7)
Similar Questions
Let S= set of point inside the sqare, T= set of points inside the triangles and C= the set of point inside the circle, if the triangle and circle intersect each other are contained in the square, then S∩T∩C=φ b. S∩T∩C=C c. S∪T∪C=S d. S∪T∩C=C
View SolutionWhich of the following numbers is inside the circle but outside triangle and square ?
 View Solution
View SolutionPower of a Point With respect to Circle when point is inside a circle
View SolutionHow many tangents can be drawn from a point lying inside a circle?
View SolutionA square and a circle are placed such that the centre of the circlelies in the centre of the square. The region inside the square butoutside the circle has the same area as the region inside the circlebut outside the square. What is the quotient between the diameterof the circle and the side of the square?
View SolutionA square is inscribed in a circle. If pr is the probability that a randomly chosen point inside the circle lies within the square and p, is the probability that the point lies outside the square, then
View Solution

