Complete Solutions to Integrated Rate Expression of chapter CHEMICAL KINETICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL KINETICS |
| A2Z | Integrated Rate Expression |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
In the reaction `2N_(2)O_(5) rarr 4NO_(2) + O_(2)`, initial pressure is `500 atm` and rate constant `K` is `3.38 xx 10^(-5) sec^(-1)`. After `10` minutes the final pressure of `N_(2)O_(5)` is
03:12View SolutionIn a first order of reaction the concentration of reactant decreases from `800 "mol"//d m^(3)` to`50 "mol"//d m^(3)` in `2 xx 10^(2) sec`. The rate constant of reaction in `"sec"^(-1)` is
02:39View SolutionThe rate constant fro a second order reaction is `8 xx 10^(-5) M^(-1) "min"^(-1)`. How long will in take a `1 M` solution to be reduced to `0.5 M`
01:54View SolutionA reaction that is of the first order with respect to reactant A has a rate constant `6 "min"^(-1)`. If we start with `[A] = 0.05 "mol" 1^(-1)`, when would `[A]` reach the value `0.05 mol 1^(-1)`
02:01View Solution……………………… reaction obeys the expresison `t_(1//2) = 1//ka` in chemical kinetics.
02:08View SolutionThe reaction `[Co (NH_(3))_(5)Br]^(2) + (H_(2)O) rarr [Co(NH_(3))_(5)(H_(2)O)]^(3+) + Br^(-)` is followed by measuring a property of the solution known as the optical density of the solution which may be taken to be linearly related to the concentration of the reactant. The values of optical density are `0.80, 0.35` and `0.20` at the end 0f `20` minutes, `40` minutes and infinite time after the start of the reaction which is first order. Calculate the rate constant.
05:29View SolutionThe rate constant for the reaction
`A rarr B` is `2 xx 10^(-4) mol^(-1)`. The concentration of `A` at which rate of the reaction is `(1//2) xx 10^(-5) M sec^(-1)` is -01:42View SolutionIn a I order reaction `A rarr` products, the concentration of the reactant decrease to `6.25%` of its initial value in `80` minutes. What is (i) the rate constant and (ii) the rate of the reaction, `100` minutes after the start, if the initial concentration is `0.2 "mole"//"litre"` ?
05:20View SolutionWhich one of the following formula represents a first-order reaction?
03:00View SolutionIn a first order reaction, the concentration of the reactant decreases form `0.8 M` to `0.4 M` in `15 min`. The time taken for the concentration to change form `0.1 M` to `0.025 M` is
03:12View SolutionThe rate constant `k`, for the reaction `N_(2)O_(5)(g) rarr 2NO_(2) (g) + (1)/(2) O_(2)(g)` is `2.3 xx 10^(-2) s^(-1)`. Which equation given below describes the change of `[N_(2)O_(5)]` with time ? `[N_(2)O_(5)]_(0)` and `[N_(2)O_(5)]_(t)` correspond to concentration of `N_(2)O_(5)` initially and at time, `t` ?
02:25View SolutionIf the rate constant for the disintegration of a radioactive nucleus is `lambda`. Therefore the probability, `P` of survival of a radioactive nucleus for one mean life is
01:47View SolutionA first-order reaction which is `30%` complete in `30` minutes has a half-life period of
01:55View SolutionThe half life for the reaction `N_(2)O_(5) hArr 2NO_(2)+1/2 O_(2)` in `24 hr` at `30^(@)C`. Starting with `10 g` of `N_(2)O_(5)` how many grams of `N_(2)O_(5)` will remain after a period of `96` hours ?
03:32View SolutionHalf-life of a reaction is found to be inversely proportional to the cube of its initial concentration. The order of reaction is
01:33View SolutionThe rate for a first order reaction is `0.6932 xx 10^(-2) mol L^(-1) "min"^(-1)` and the initial concentration of the reactants is `1M`, `T_(1//2)` is equal to
01:44View Solution`99%` of a first order reaction was completed in `32 min`. When will `99.9%` of the reaction complete.
02:09View SolutionFor which order reaction a straight line is obtained along with `x`-axis by plotting a graph between half-life `(t_(1//2))` and initial concentration `'a'`
01:29View SolutionWhich graph represents zero-order reaction `[A(g) rarr B (g)]` ?
03:15View Solution……………………… reaction obeys the expresison `t_(1//2) = 1//ka` in chemical kinetics.
02:08View Solution`t_(1//4)` can be taken as the time taken for concentration of reactant to drop to `.^(3)//_(4)` of its initial value. If the rate constant for a first order reaction is `K`, then `t_(1//4)` can be written as:
02:36View SolutionA reaction that is of the first order with respect to reactant A has a rate constant `6 "min"^(-1)`. If we start with `[A] = 0.5 "mol" 1^(-1)`, when would `[A]` reach the value `0.05 mol 1^(-1)`
02:01View SolutionA first-order reaction was started with a decimolar solution of the reactant, `8` minutes and `20 `seconds later its concentration was found to `M//100`. So the rate of the raction is
01:50View SolutionA first order reaction is half completed in `45` minutes. How long does it need `99.9%` of the reaction to be completed
02:32View SolutionThe rate constant of reaction `2 A + B rarr C` is `2.57 xx 10^(-5) L "mole"^(-1) sec^(-1)` after `10 sec`, `2.65 xx 10^(-5) L "mole"^(-1)sec^(-1)` after `20sec` and `2.55 xx 10^(-5) L "mole"^(-1) sec^(-1)` after `30 sec`. The order of the reaction is :
02:40View SolutionDecay constant of a reaction is `1.1 xx 10^(-9)//sec`, then the half-life of the reaction is
01:09View SolutionA follows first order reaction.
`(A) rarr Product`
The concentration of `A` changes form `0.1 M` to `0.025 M` in `40 min`. Find the rate of reaction of `A` when the concentration of `A` is `0.01 M`.02:07View SolutionGaseous `N_(2)O_(5)` decomposes according to the following equation:
`N_(2)O_(5)(g) rarr 2NO_(2)(g) + (1)/(2)O_(2)(g)`
The experimental rate law is `-Delta [N_(2)O_(5)]//Delta t = k[N_(2)O_(5)]`. At a certain temerature the rate constant is `k = 5.0 xx 10^(-4) sec^(-1)`. In how seconds will the concentration of `N_(2)O_(5)` decrease to one-tenth of its initial value ?02:44View SolutionWhich of the following curve represent zero order reaction of `A rarr` products ?
02:06View Solution`t_(1//2) =` constant confirms the first order of the reaction as one `a^(2)t_(1//2) =` constant confirms that the reaction is of
02:33View SolutionIn presence of `HCl`, sucrose gets hydrolysed into glucose and fructose. The concentration of sucrose was found to reduce form `0.4 M` to `0.2 M` in `1` hour and `0.1 M` in `2` hours. The order of the reaction is
01:46View SolutionConsider a reaction `A(g) rarr 3B(g) + 2C(g)` with rate constant is `1.386 xx 10^(-2) "min"^(-1)` in a non-rigid closed container starting with `2` moles of `A` in `12.5 L` vessel initially, if reaction is allowed to take place at constant pressure and at `298 K` the conc. of after `100 min` is
02:45View SolutionFor the reaction `A + 2B rarr` products (started with concentration taken in stoichiometric proportion), the experimentally determined rate law is :
`-(d[A])/(d t) = ksqrt([A])sqrt([B])`
The half life time of the reaction would be :02:14View SolutionA reaction `2A + B overset(k)rarr C+ D` is first order with respect to `A` and 2nd order with respect to `B`. Initial conc. `(t = 0)` of `A` is `C_(0)` while `B` is `2C_(0)`. If at `t` as `30` minutes the conc. of `C` is `C_(0)//4`, then rate expression at `t = 30` minutes is:
04:18View SolutionThe time for half-life period of a certain reaction, `A rarr` products is `1 h`. When the initial concentration of the reactant `'A'` is `2.0 "mol" L^(-1)`, how much time does it take for its concentration to come from `0.50` to `0.25 "mol" L^(-1)`, if it is zero order reaction ?
03:05View SolutionWhat will be the order of reaction and rate constant for a chemical change having `log t_(50%)` versue log concentration of `(a)` curves as:
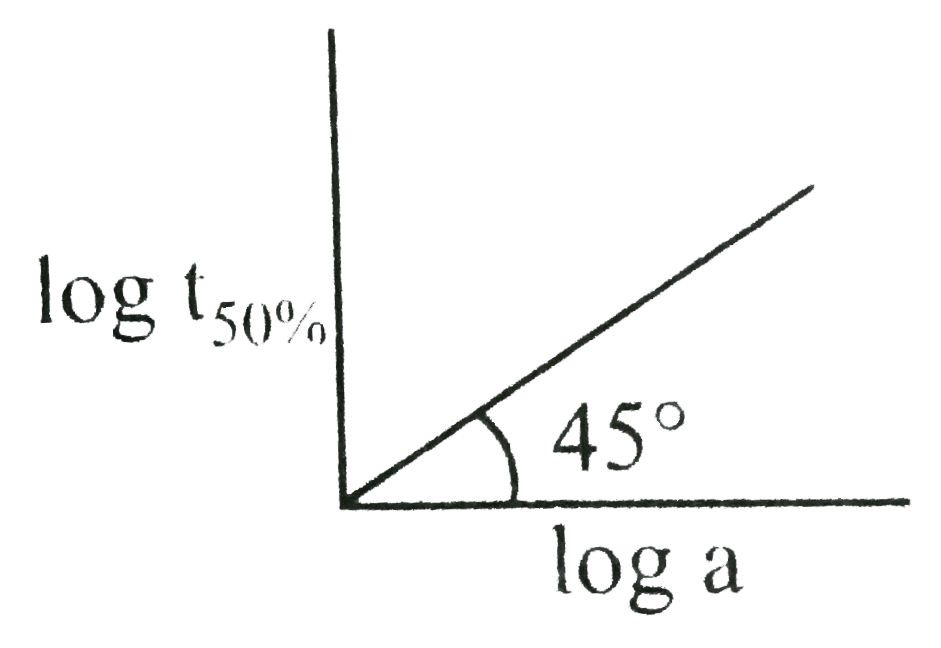 06:14View Solution
06:14View SolutionIf `75%` of a first order reaction completed in `15 min`. Then `90%` of the same reaction completed in
02:30View SolutionThe half-life period of a first-order chemical reaction is `6.93 min`. The time required for the completion of `99%` of the chemical reaction will be `(log 2 = 0.301)`
01:58View SolutionThe half-life for a reaction at initial concentration of `0.5` and `1.0 "mole litre"^(-1)` are `200 sec` and `100 sec` respectively. The order of the reaction is
03:07View Solution`75%` of a first-order reaction was completed in `32` minutes, when was `50%` of the reaction completed ?
00:46View SolutionA drop of solution (volume `0.05 mL`) contains `3 xx 10^(-6) "mole" H^(o+)` ions. If the rate constant of disappearance of `H^(o+)` ions is `1 xx 10^(7) mol L^(-1) s^(-1)`, how long would it take for `H^(o+)` ions in the drop of disappear?
02:45View SolutionA certain zero order reaction has `k = 0.025 M s^(-1)` for the disappearance of `A`. What will be the concentration of `A` after `15` seconds if the initial concentration is `0.5 M` ?
01:21View SolutionFor a certain reaction the variation of rate constant with temperature is given by the equation
`ln k_(t) = lnk_(0) + ((ln 3)t)/(10) (t ge 0^(@)C)`
The value of temperature coefficient of the reaction is02:11View SolutionA certain substance `A` is mixed with an equimolar quantity of substance `B`. At the end of an hour `A` is `75%` reacted. Calculated the time when `A` is `10%` unreacted. (Given order of reaction is zero).
03:28View SolutionThermal decomposition of compound `x` is a first order reaction. If `75%` of `x` is decomposed in `100 min`. How long will it take for `90%` of the compound to decompose ? Given `log 2=0.30`
02:44View SolutionFor a first order reaction, the reaction, the plot of `log C` against 't' (log C vs 't') gives a straight line with slope equal to:
02:26View SolutionIn a certain reaction, `10%` of the reactant decomposes in one hour, `20%` in two hours, `30%` in theee hours, and so on. The dimenison of the velocity constant (rate constant) are
03:37View SolutionIf for a reaction in which `A(g)` converts to `B(g)` the reaction carried out at const.
`V` & `T` results into the following grapg.
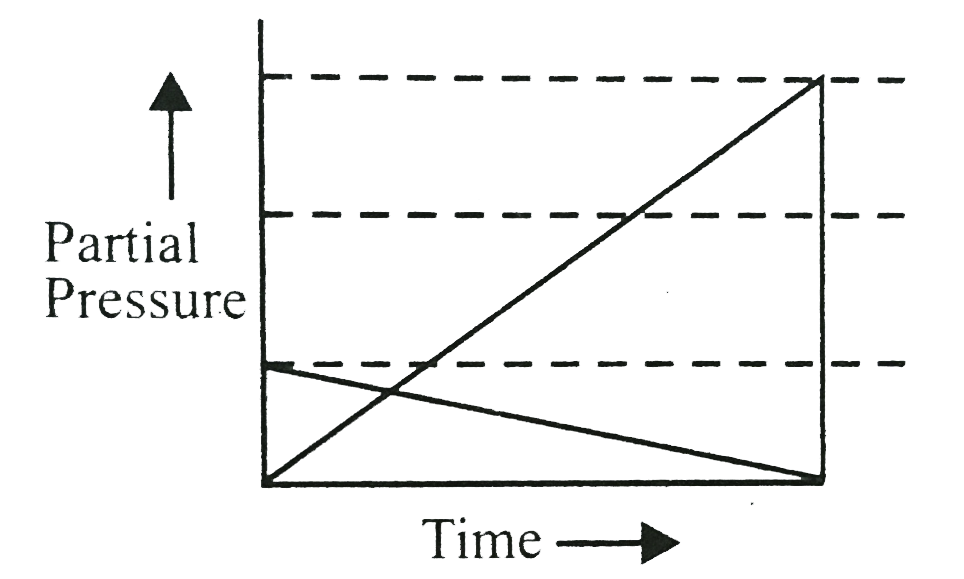 01:50View Solution
01:50View SolutionIn a first order of reaction the reacting substance has half-life period of ten minutes. What fraction of the substance will be left after an hour the reaction has occurred ?
01:55View SolutionThe reaction `A overset (k)rarr` Products, is zero order while the reaction `B overset (k) rarr` Products, is 1st order. For what initial concentration of `A` the half-lives of the two reactions are equal.
01:26View SolutionIf a I-order reaction is completed to the extent of `60%` and `20%` in time intevals, `t_(1)` and `t_(2)`, what is the ratio, `t_(1) : t_(2)`?
01:27View SolutionWhich of the followoing expression is correct for first order reaction ? `(CO)` refers to initial concentration of reactant.
00:53View SolutionFor a reaction `A rarr` Products, the concentration of reactant are `C_(0), aC_(0), a^(2)C_(0), a^(3)C_(0)`……after time interval `0, t, 2t`…..where `'a'` is constant. Then :
02:09View Solution
Integrated Rate Expression questions and complete solutions for chapter CHEMICAL KINETICS of A2Z CHEMISTRY (HINGLISH) of Class 12
All Exercises from A2Z Class 12 CHEMISTRY CHEMICAL KINETICS
- AIIMS Questions
- AIPMT/NEET Questions
- Arrhenius Equation, Effect Of Temprature And Effect Of Catalysts
- Assertion-Reasoning Questions
- Initial Rate Method And Ostwaid Method
- Integrated Rate Expression
- Parallel Reaction, Consecutive Reaction, Special Cases Of First-Order Reactions
- Rate Expression, Rate Of Appearance And Disappearance, Instaneous And Average Rate Of Reaction
- Rate Law, Law Of Mass Action, Order Of The Reaction, And Molecularity
- Section B - Assertion Reasoning
- Section D - Chapter End Test
