Complete Solutions to Problems Based On Mixed Concepts of chapter SOURCE AND EFFECT OF MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SOURCE AND EFFECT OF MAGNETIC FIELD |
| A2Z | Problems Based On Mixed Concepts |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Consider following coils each of one turn carrying current `I`. The magnitude of the magnetic induction at `X,Y,Z` are `B_(1),B_(2)` and `B_(3)` respectively. Then (assume side of square to be same in each case)
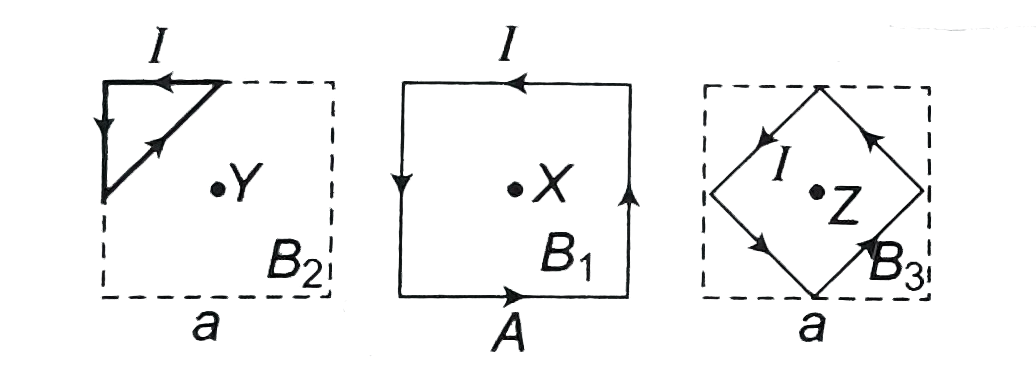 01:56View Solution
01:56View SolutionTwo wires wrapped over a conical frame from the coils `1` and `2`. If they produce no net magnetic field at the apex `P`, the value of
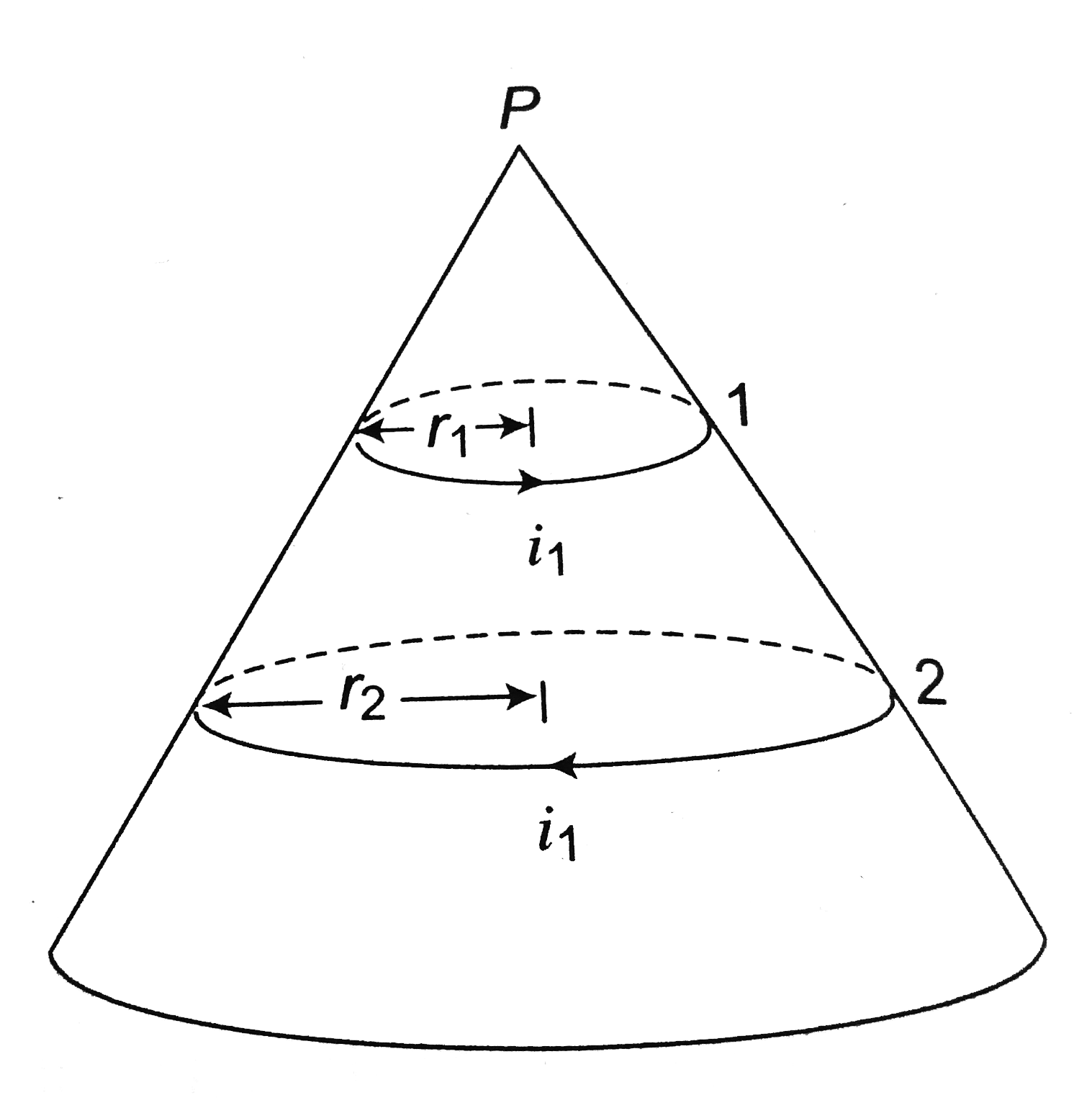 04:59View Solution
04:59View SolutionTwo wires are wrapped over wooden cylinder to form two co-axial loops carrying currents `i_(1)` and `i_(2)`. If `i_(2)=8i_(1)` the value of `x` for `B=0` at the origin `O` is:
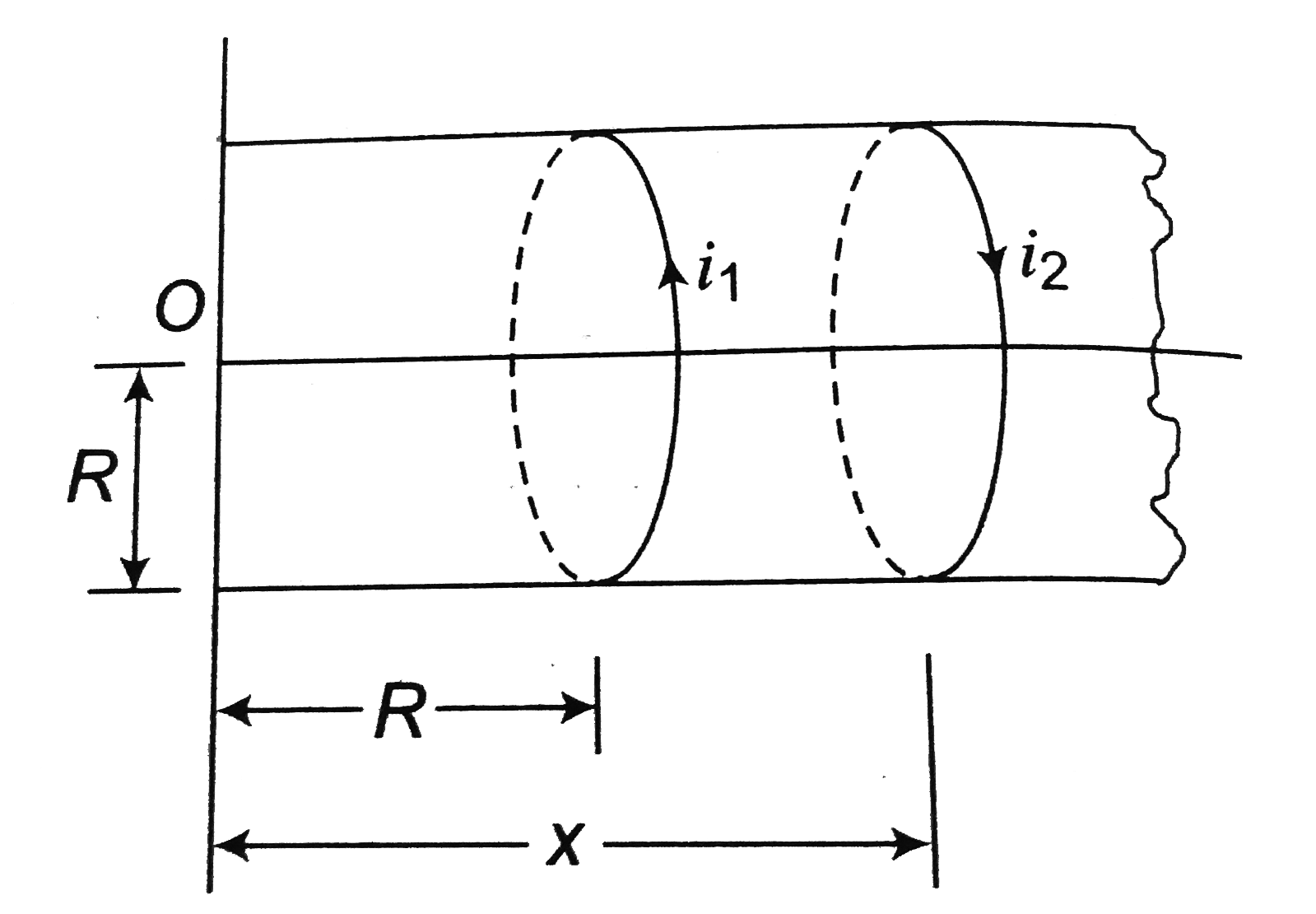 04:09View Solution
04:09View SolutionDetermine the magnetic field at the centre of the current carrying wire arrangement shown in Fig. The arrangement extends to infinity. (The wires joining the successive squares are along the line passing through the centre).
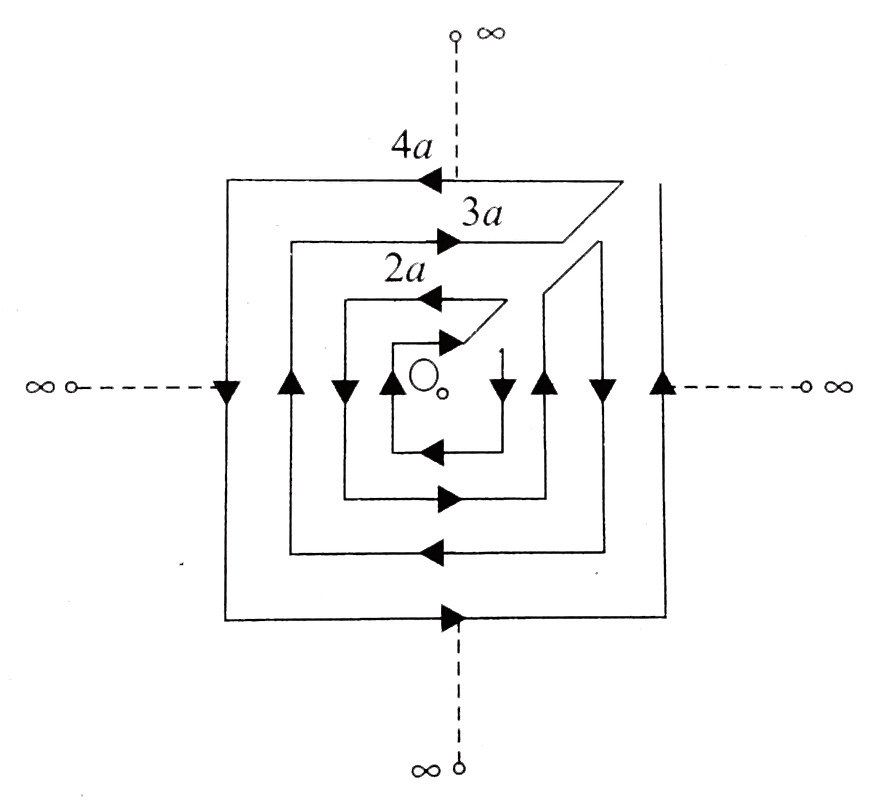 05:53View Solution
05:53View SolutionEqual currents `i=1` A are flowing through the wires parallel to y-axis located at `x=+1m, x=+2m, x=+4m` and so on...., etc. but in opposite directions as shown in Fig The magnetic field (in tesla) at origin would be
 03:46View Solution
03:46View SolutionIn Fig. , AB is a non-conducting rod. Equal charges of magnitude q are fixed at various points on the rod as shown. The rod is rotated uniformly about an axis passing through O and perpendicular to its length such that linear speed at the end A or B of the rod is `3 ms^(-1)`. Magnetic field at O is
 05:09View Solution
05:09View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
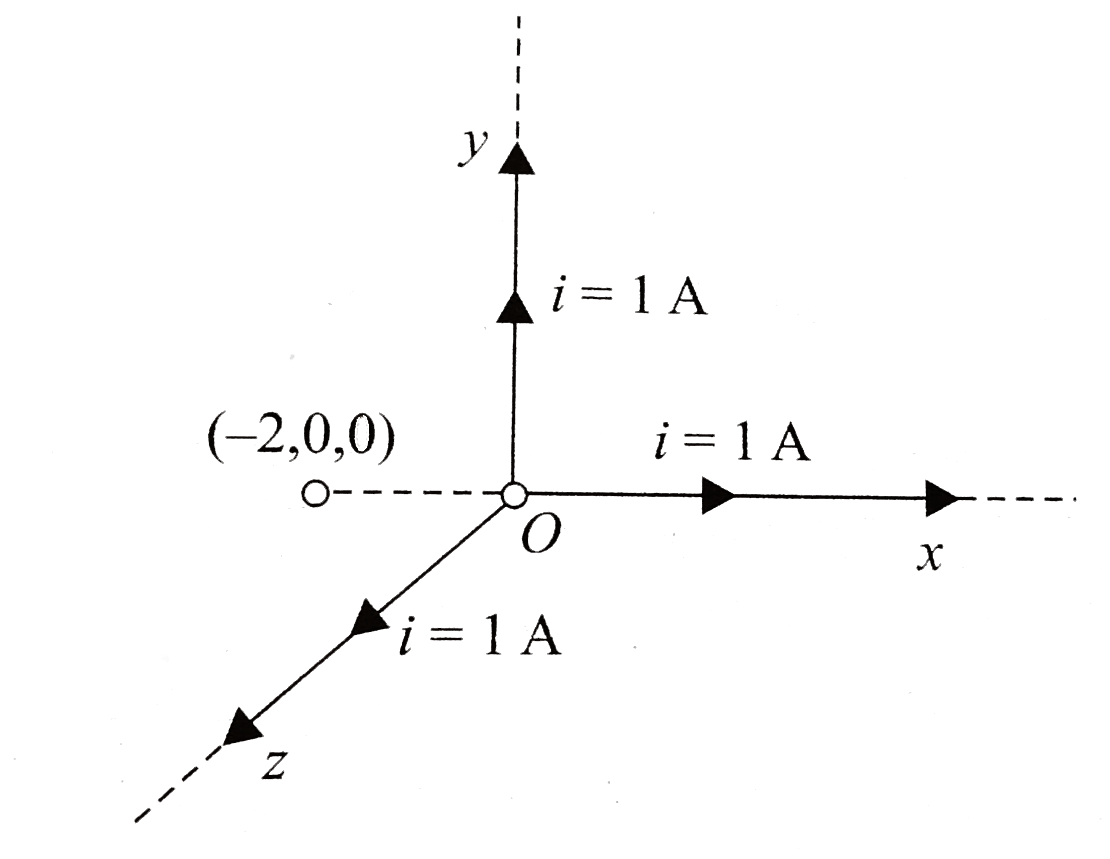 04:51View Solution
04:51View SolutionInfinite wires, each carrying a current 0.5 A, are kept parallel to y-axis and intersecting x-axis at `x=+-1` m, `+02 m`, `+-4 m`, `+-8m` etc. Wires kept at positive values of x carry current in the same direction while wires kept at negative values of x carry current successively in opposite directions as shown in Fig.
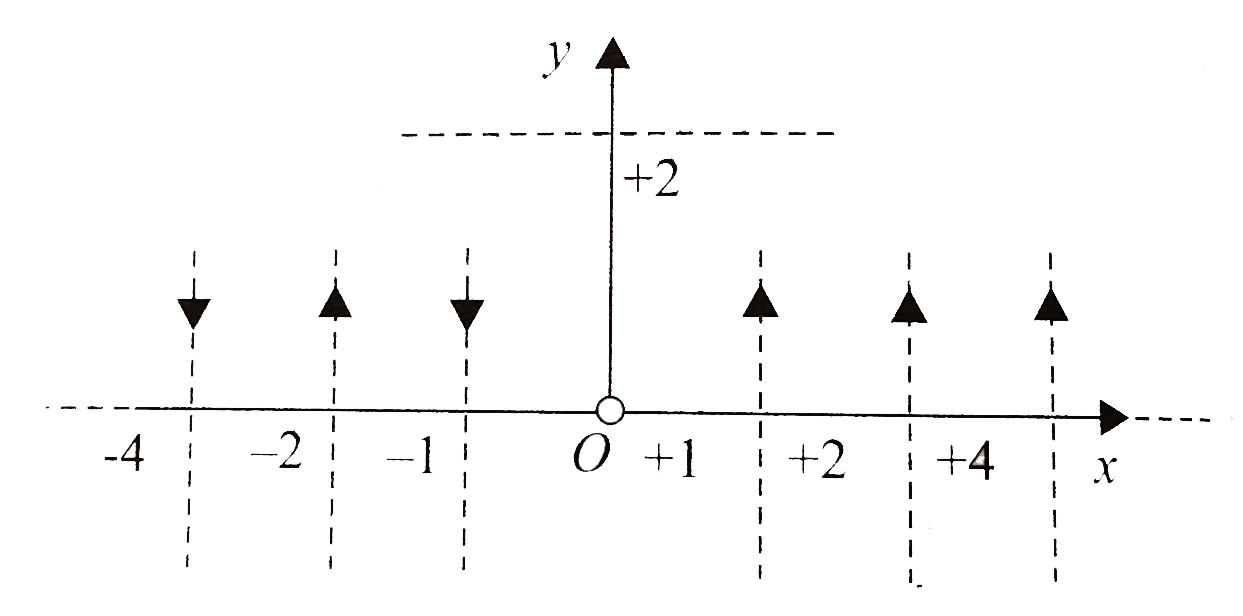
A wire is kept parallel to x-axis and intersecting y-axis at y=2 m. It carries a current i. Assuming this wire to be insulated from others then the current i in it such that magnetic induction at O is zero is
(assuming each wire to be infinitely long)07:25View SolutionA current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.
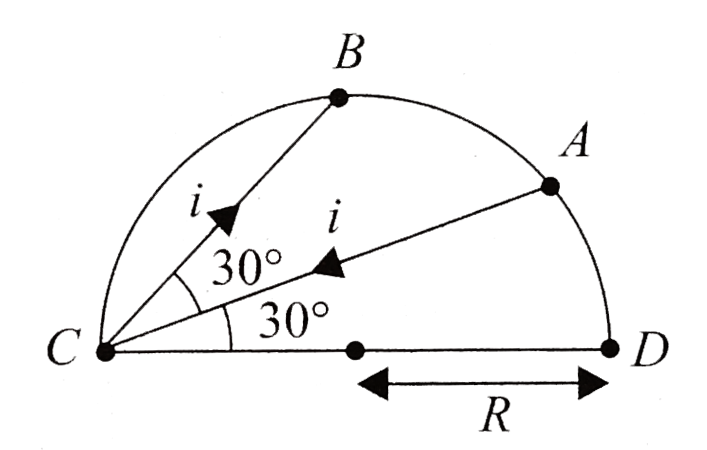 08:33View Solution
08:33View SolutionIn the figure a charged small sphere of mass `m` and the charge `q` starts sliding from rest on a vertical fixed circular smooth track of radius `R` from the position `A` shown. There exist a uniform magnetic field of `B`. Find the maximum force exerted by track on the sphere during its motion.
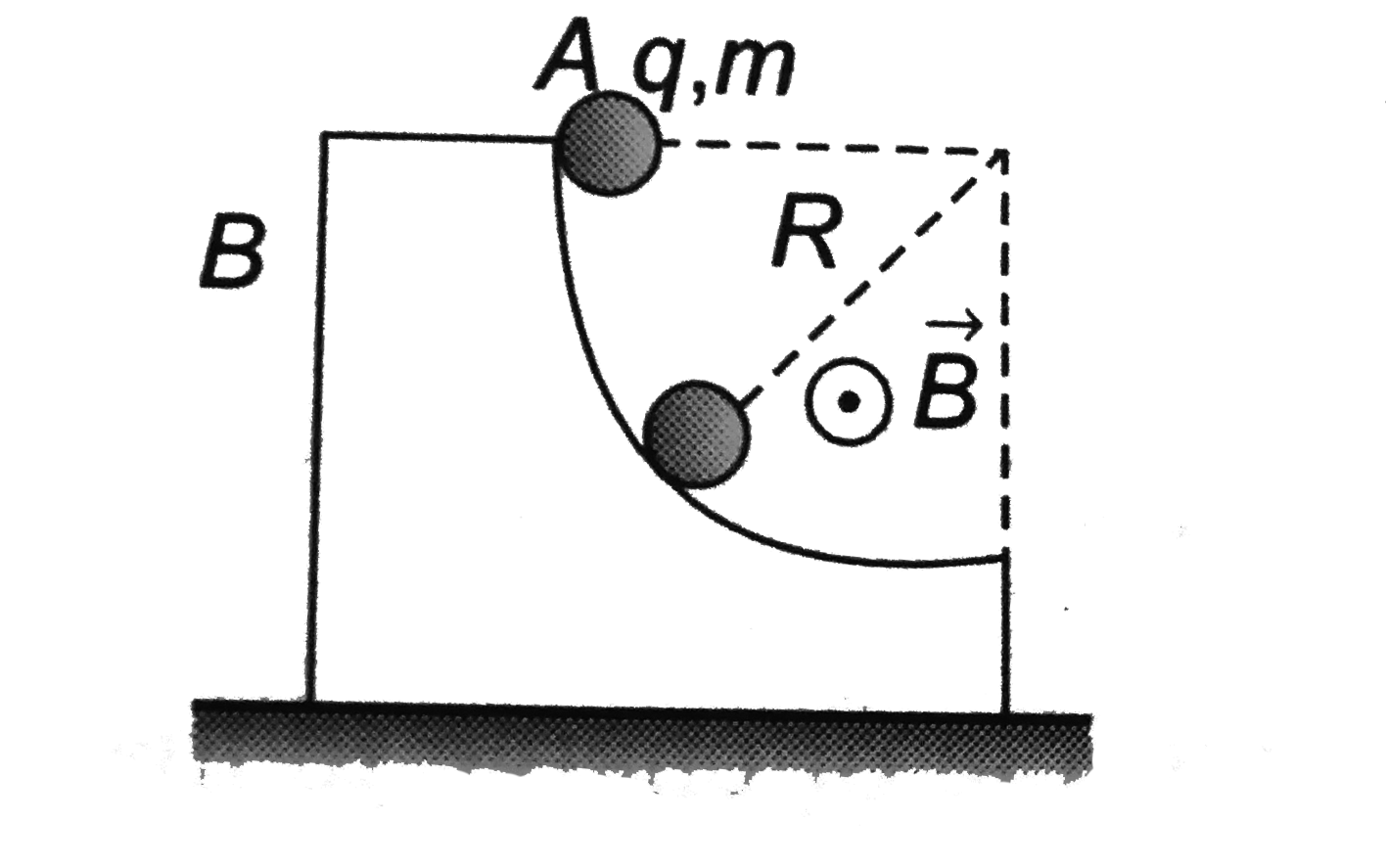 03:35View Solution
03:35View SolutionIn a cylinderical region uniform magnetic field is present as shown in the figure. The cylinder is kept on a horizontal plane and its axis is horizontal. If a charge particle of mass `m` and charge `q` is projected horizontally with velocity `v` through a hole normal to the axis of the cylinder as shown in the diagram. An observer states the particle moves first undeviated and subsequently. oscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period
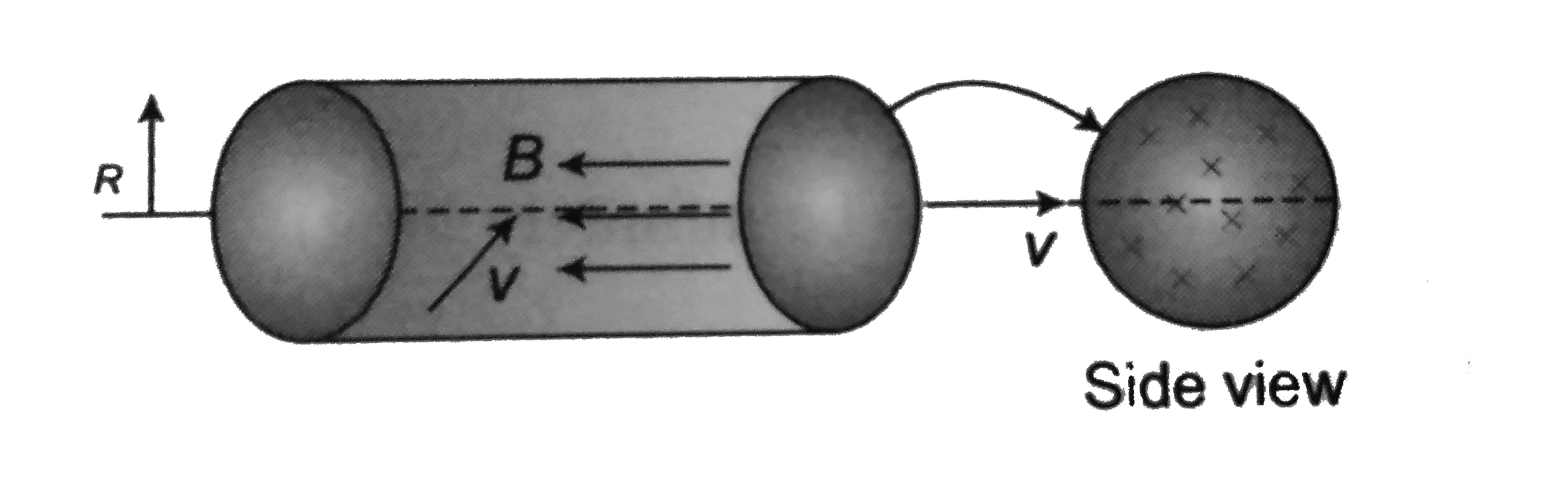 02:40View Solution
02:40View SolutionAn electron moving with a velocity `v` along the positive `x`-axis approaches a circular current carrying loop as shown in the fig. the magnitude of magnetic force on electron at this instant is
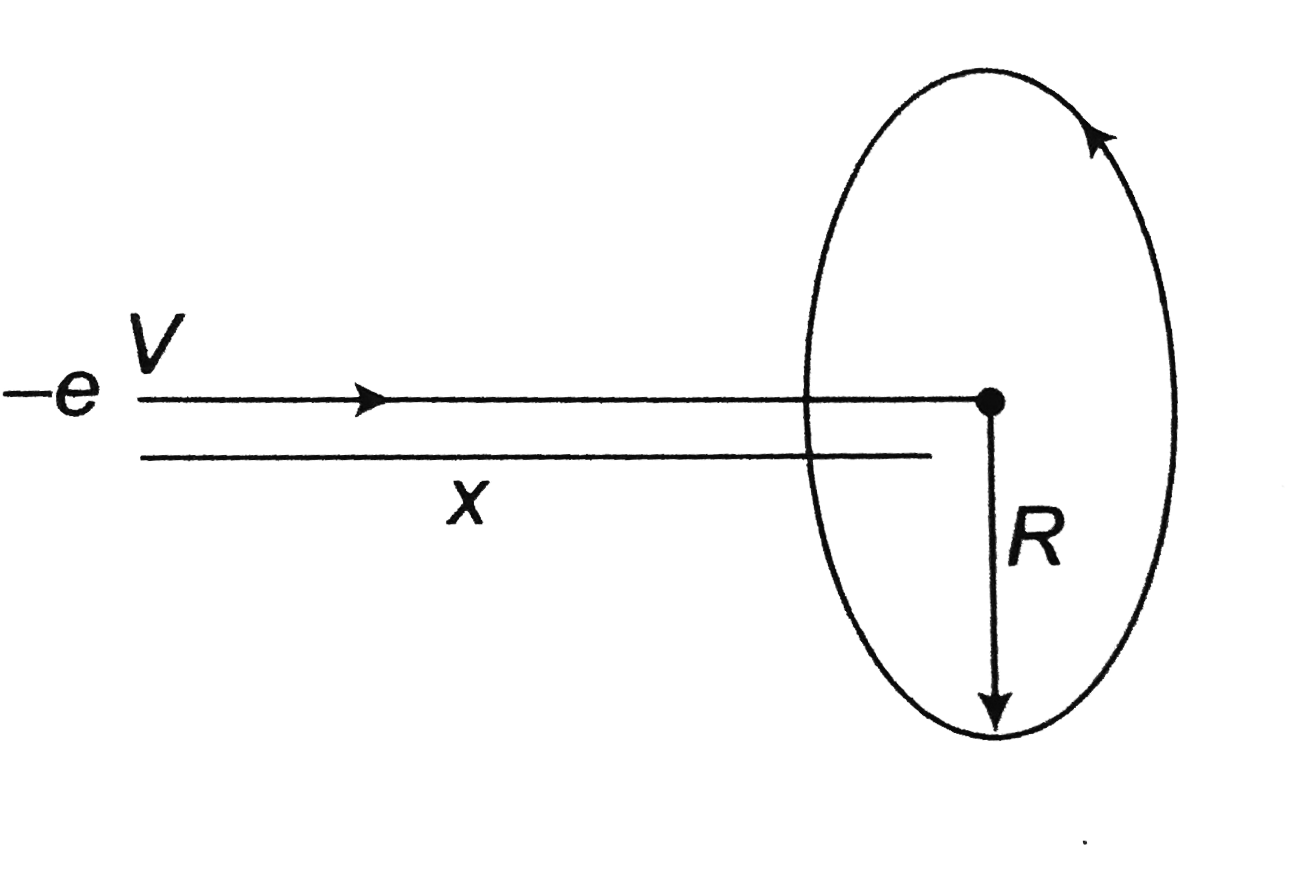 02:41View Solution
02:41View SolutionIf a charged particle of charge to mass ratio `(q/m) = alpha` centers in a magnetic field of strength B at a speed `v=(2 alpha d) (B),` then
 02:45View Solution
02:45View SolutionA conducting ring of mass 2kg and radius `0.5m` is placed on a smooth plane. The ring carries a current of `i=4A`. A horizontal magnetic field `B=10 T` is switched on at time `t=0` as shown in fig The initial angular acceleration of the ring will be
 .03:27View Solution
.03:27View SolutionA point charge is moving in clockwise direction in a circle with constant speed. Consider the magnetic field produced by the charge at a fiexed point P (not at the centre of circle ) on the axis of the circle. Then,
03:31View SolutionAn `alpha` is moving along a circle of radius R with a constant angular velocity `omega`. Point A lies in the same plane at a distance 2R from the centre. Point A records magnetic field produced by the `alpha`-particle. If the minimum time interval between two successive time at which A records zero magnetic field is t, the angular speed `omega`, in terms of t, is
03:06View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is
 02:44View Solution
02:44View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and `1Vm^-1` respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity `1ms^-1` along x-axis and is at origin at t=0. Then, the coordinates of the particle at time `pis` will be
04:08View SolutionA uniform magnetic field of magnitude `1T` exists in region `yge0` along `hatk` direction as shown. A particle of charge `1C` is projected from point `(-sqrt(3),-1)` towards origin with speeds `1 m//sec`. If mass of particle moves are:
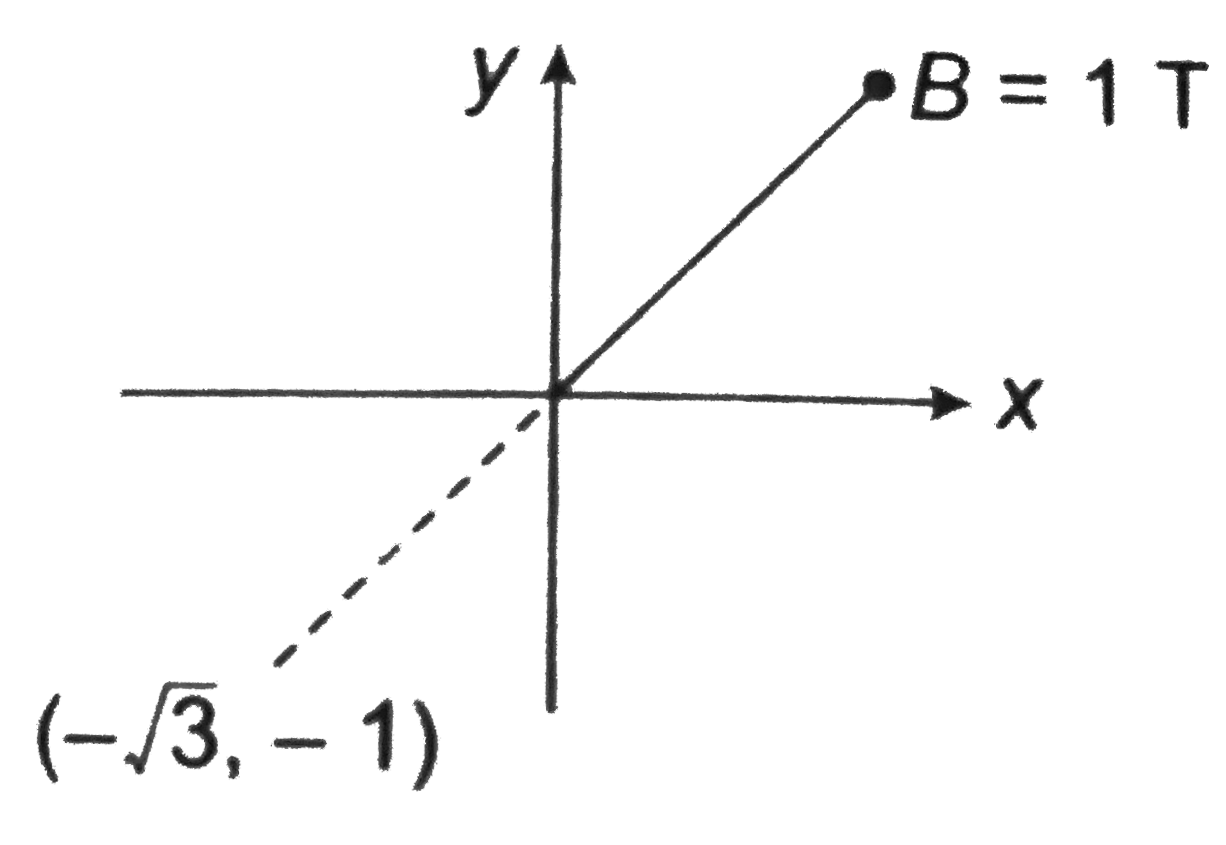 03:10View Solution
03:10View SolutionA uniform magnetic field exist in a region which forms an equilateral triangle of side a. The magnetic field is perpendicular to the plane of the triangle . A charged q enters into this magnetic field perpendicular to a side with speed v. The charge enters from midpoint and leaves the field from midpoint of other side. Magnetic induction in the triangles is
02:25View SolutionA charge particle is moving in a circular path in a magnetic field. A resistive force starts acting on the particle whose direction is oppositely directed to its motion and magnitude is directely proportional to its velocity. Now the particle starts moving in a spiral path, then
04:01View SolutionA square loop `ABCD` of side `'a'` carrying current `I` is folded about an axis passing through its centre (`y`-axis). The two halves are inclined at angle `30^(@)` with `xy` plane as shown. Find the magnetic field at origin. The origin coincides with the centre of loop.
 06:05View Solution
06:05View SolutionA long insulated copper wire is closely wound as a spiral of `N` turns. The spiral has inner radius a and outer radius `b`. The spiral lies in the `xy`-plane and a steady current I flows through the wire. The`z`-component of the magnetic field at the centre of the spiral is
 08:01View Solution
08:01View SolutionA `3D` structure of current carrying wire is as shown in the figure.
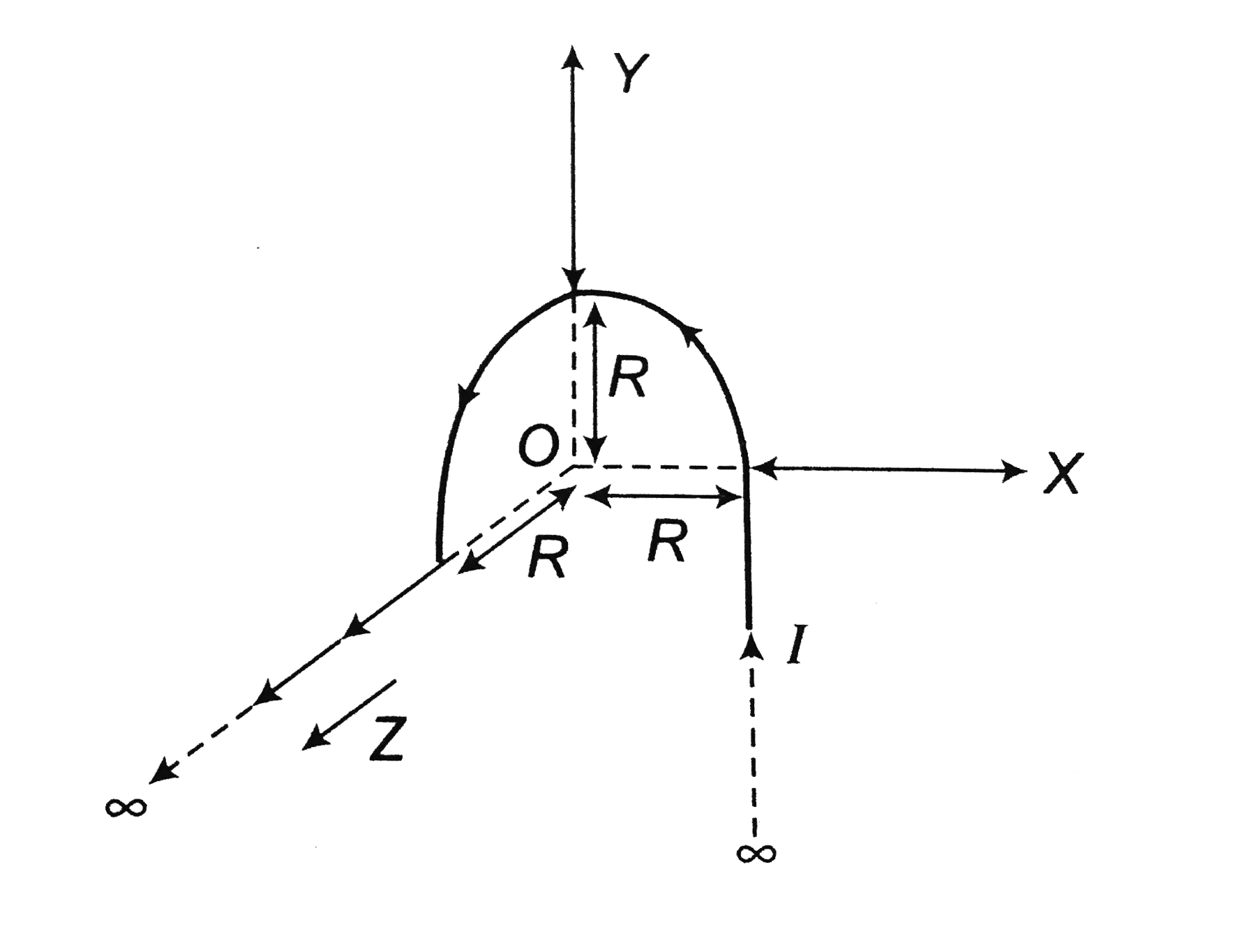
The magnetic force experienced by a charge particle of mass `m` and charge `q`, when it is crossing origin with velocity `vec(v)` along positive `Y`-axis will be05:39View SolutionThe electric field acts positive `x`-axis. A charged particle of charge `q` and mass `m` is released from origin and moves with velocity `vec(v)=v_(0)hatj` under the action of electric field and magnetic field, `vec(B)=B_(0)hati`. The velocity of particle becomes `2v_(0)` after time `(sqrt(3)mv_(0))/(sqrt(2)qE_(0))`. find the electric field:
04:31View SolutionA magnetic field `vec(B)=-B_(0)hati` exists within a sphere of radius `R=v_(0)T sqrt(3)` where `T` is the time period of one revolution of a charged particle starting its motion from origin and moving with a velocity `vec(v)_(0)=(v_(0))/2sqrt(3)hati-(v_(0))/2 hatj`. Find the number of turns that the particle will take to come out of the magnetic field.
04:35View SolutionA particle of mass `m` and charge `q` travelling at a velocity `v` along `x`-axis at time `t=0`. It enters a region in which electric field, `E` is present along `z`-axis and magnetic field, `B` is present along `y`-axis. The distance covered upto time `t=0.2xx10^(-1) sec,` along `x`-axis is `v//50` (in meters). find the value of `v`:
 02:16View Solution
02:16View SolutionThe electric field is swiched off at time `t=0.2xx10^(-1) sec`. What will be the postion of the particle at time `t_(0)=0.6xx10^(-1) sec`, if the ration of initial velocity, `v` to the radius of the curve traced by the particle is `(100 pi)/4`?
02:53View SolutionA particle of specific charge `q/m=pi C//kg` is projected from the origin towards positive `x`-axis with a velocity of `10 m//s ` in a uniform magnetic field `vec(B)=-2hatk T`. The velocity `vec(v)` of particle after time `t=1/12 s` will be (in `m//s`)
03:02View SolutionA neutral particle is initally at rest in a uniform magnetic field `B` as shown in the diagram. The particle then spontaneously decays into two fragments, one with a positive charge `+q` and mass `3m` and the other with negative charge `-q` and mass `m`. Neglecting the interaction between the two charged particles and assuming that the speeds are much less than speed of light, determine the time (in `mus`) after the decay at which the two fragments first meet. (use the following data `q=1 muC B=2pimuT, m=10^(-15) kg`). Both the charges have initial velocity in `x-y` plane.
 06:31View Solution
06:31View SolutionA `U`-shaped wire of mass `m` and length `l` is immersed with its two ends in mercury (see figure). The wire is in a homogenous field of magnetic induction `B`. if a charge, that is, a current pulse `q=int idt`, set through the wire, the wire will jump up.

If the wire reaches height `h` calculate the magnitude of the charge or current pulse, assuming that the time of the current pulse is very small in comparision with the time of flight. Make use of the fact that impulse of force equals
`intFdt`, which equal `mv`. Evalute `q` for `B=0.1 Wb//m^(2), m=10 gm,l=20cm & h=3` meters.03:01View SolutionA particle of charge per unit mass `alpha` is released from origin with a velocity `vecv=v_(0)hati` in a magnetic field
`vec(B)=-B_(0)hatk` for `xle(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
and `vec(B)=0` for `xgt(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
The `x`-coordinate of the particle at time `t((pi)/(3B_(0)alpha))` would be03:27View Solution
Problems Based On Mixed Concepts questions and complete solutions for chapter SOURCE AND EFFECT OF MAGNETIC FIELD of A2Z PHYSICS (HINGLISH) of Class 12
All Exercises from A2Z Class 12 PHYSICS SOURCE AND EFFECT OF MAGNETIC FIELD
- AIIMS Questions
- AIPMTNEET Questions
- Assertion- Reason
- Force On A Current Carrying Conductor In Magnetic Field
- Magnetic Dipole
- Magnetic Field Due To Circular Arc
- Magnetic Field Due To Current
- Motion Of Charged Particle In Magnetic Field
- Problems Based On Mixed Concepts
- Section B - Assertion Reasoning
- Section D - Chapter End Test