Complete Solutions to EXERCISE # II of chapter FLUID MECHANICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FLUID MECHANICS |
| BANSAL | EXERCISE # II |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
The tank in fig discharge water at constant rate for all water levels above the air inlet `R` The height above datum to which water would rise in the manometer tubes `M` and `N` respectively are `_______&________`
 View Solution
View Solution`A` solid cube, with faces either vertical or horizontal, is floating in a liquid of density `6g//c c`. It has two third of its volume submerged. If enough water is added from the top so as to completely cover the cube, what fraction of its volume will remain immersed in the liquid?
08:07View SolutionA glass beaker is placed partially filled with water in a sink it has a mass of 390 gm and an interior volume of `500 cm^(2)` when water starts filling the sink, it is found that if beaker is less than half full it will float but if it is more than half full it remains on the bottom of the sink as the water rises to its rim, what is the density of the material of which the beaker is made?
07:01View SolutionA wooden cylinder of diameter 4 r, height H and density `rho//3` is kept on a hole of diameter 2 r of a tank, filled with water of density `rho` as shown in the

The block in the above question is maintained by external means and the level of liquid is lowered. The height `h_(2)` when this external force reduces to zero is
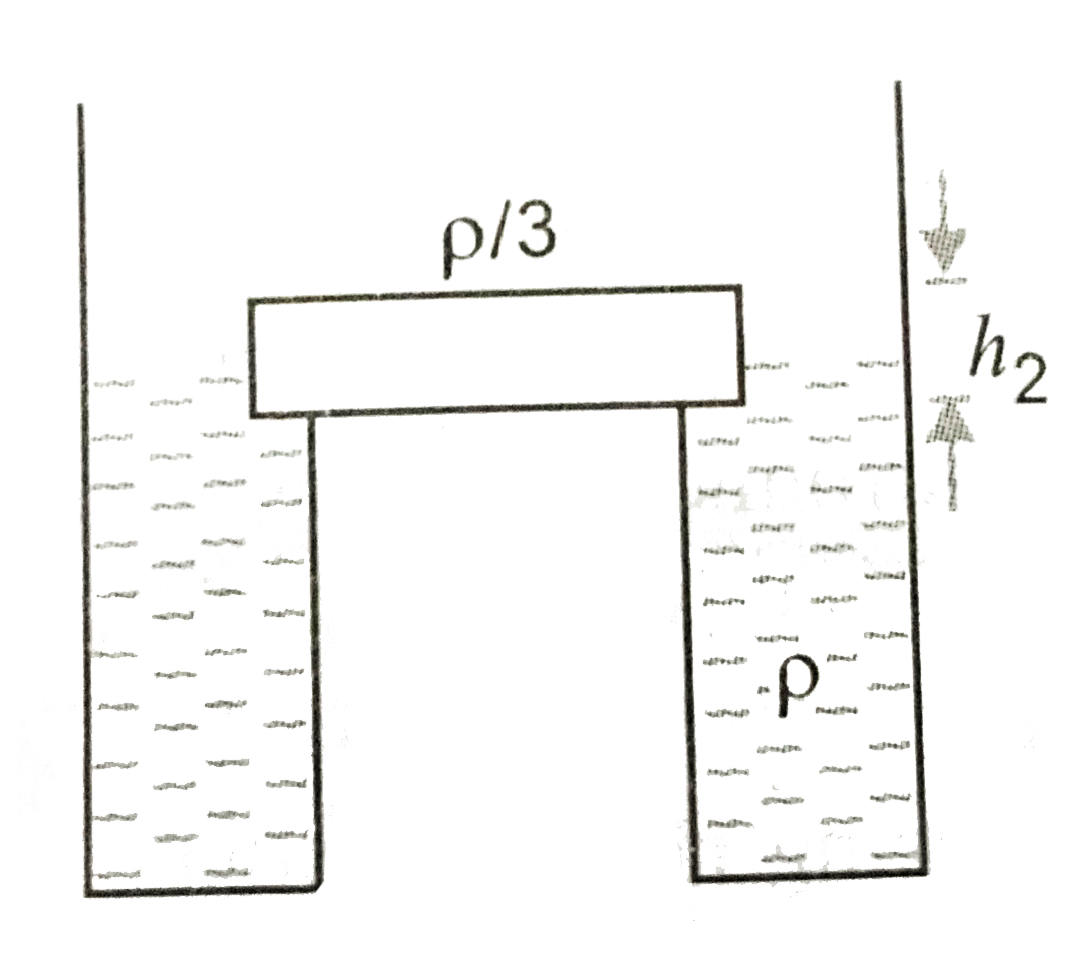 03:34View Solution
03:34View Solution`A` cylindrical rod of length `l=2m &` density `(rho)/(2)` floats vertically in a liquid of density `rho` as shown in Fig (a)
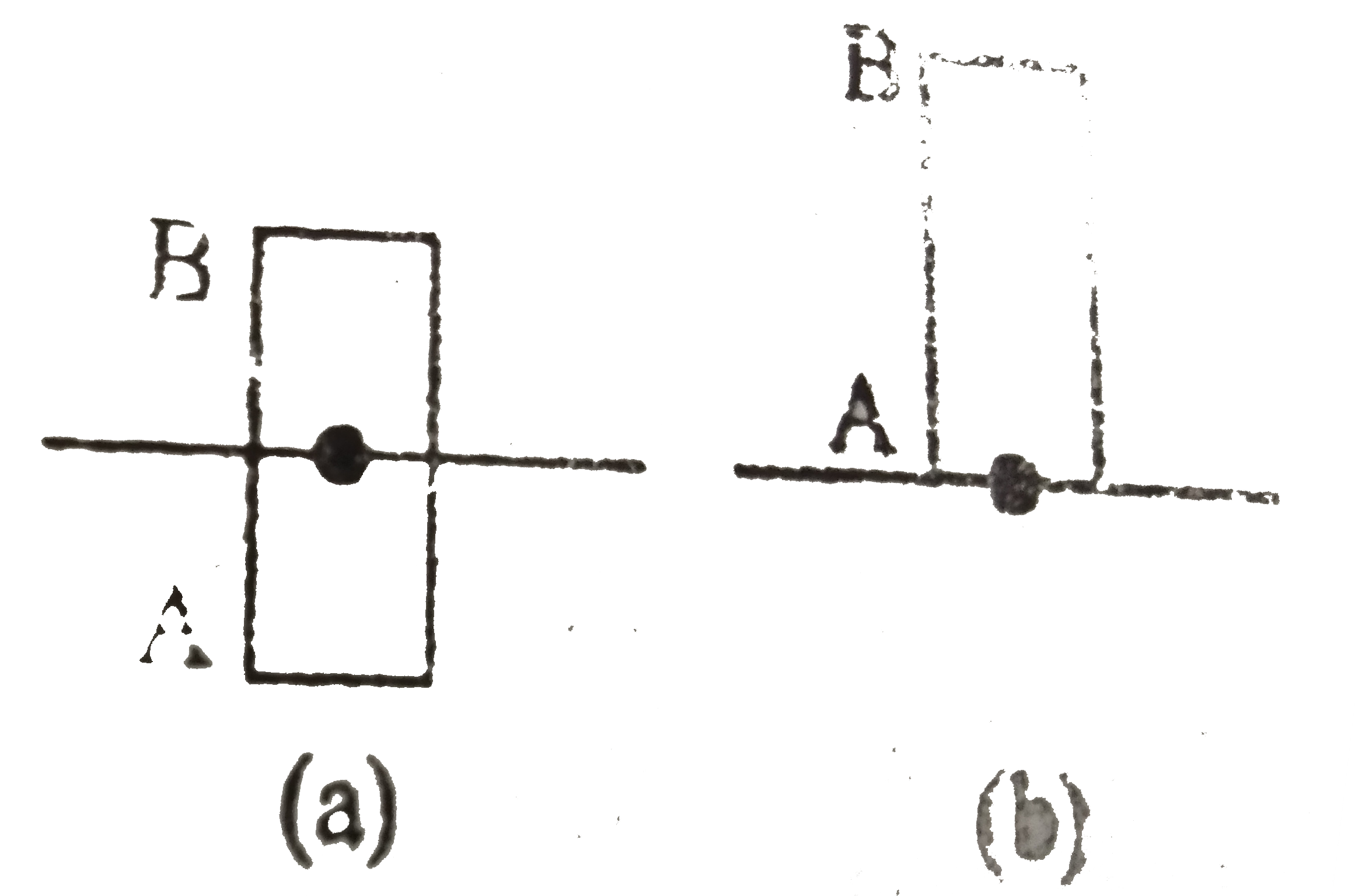
(a) Show that it performs `SHM` when pulled slightly up `&` released `&` find its time period. Neglect change in liquid level.
(b) Find the time taken by the rod to completely immerse when released from position showm in (b). Assume that it remains vertical throughout its its motion `("take" g=pi^(2)m//s^(2))`View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density `d_(1)`of the rod is smaller than the density `d_(2)` of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
 08:41View Solution
08:41View Solution`A` hollow cone floats with its axis vertical upto one third of its height in a liquid in a liquid of relative density `0.8` and with its vertex submerged. When another liquid of relative density `rho` is filled in it upto one third of its height, the cone floats upto half its vertical height. The height of the cone is `0.10m` and the radius of the circular base is `0.05m`. Find the specific gravity `rho` is given.
View SolutionIn the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities `2rho` and `3rho`. The height h for the equilibrium of cylinder must be
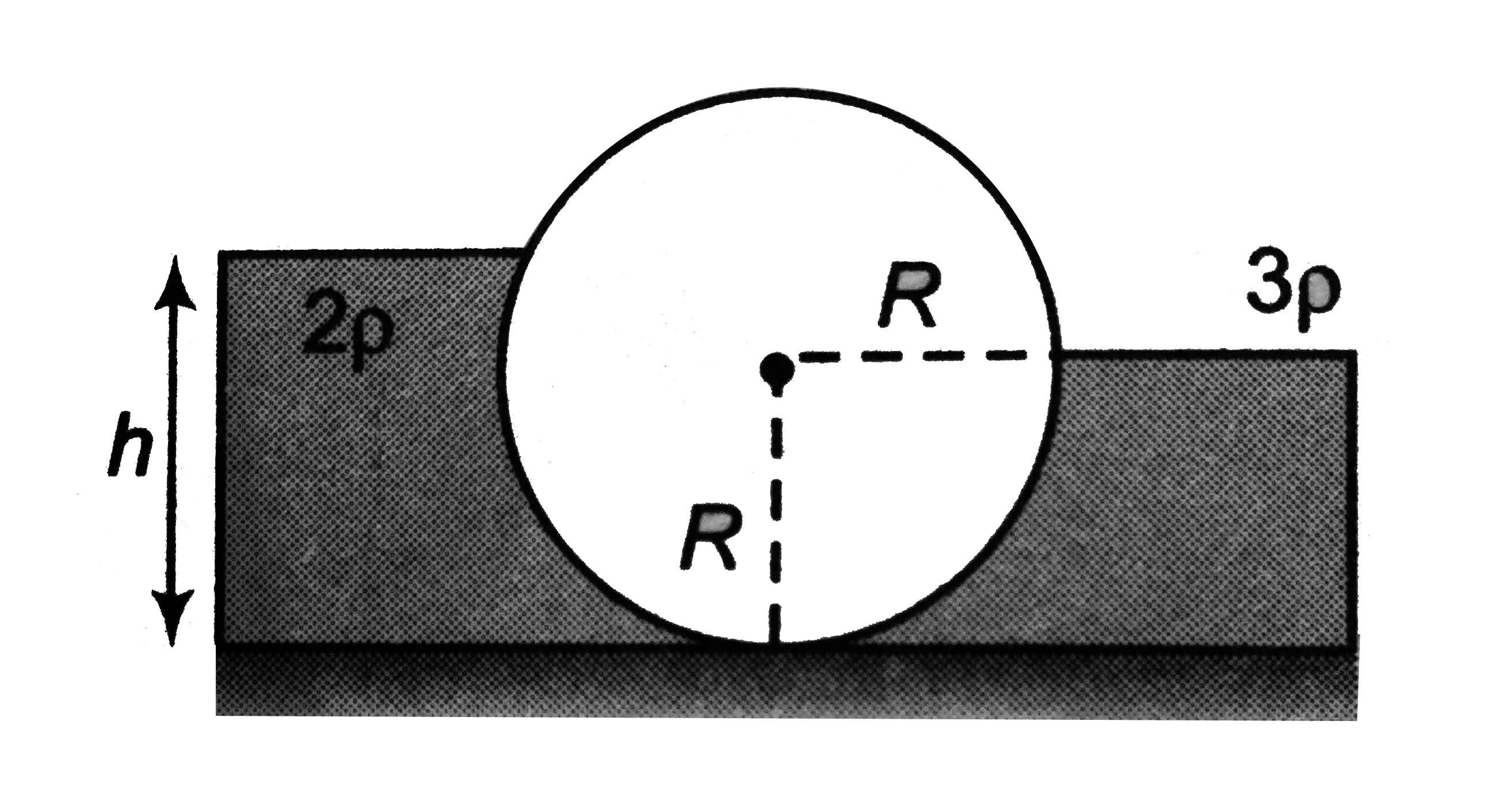 04:52View Solution
04:52View Solution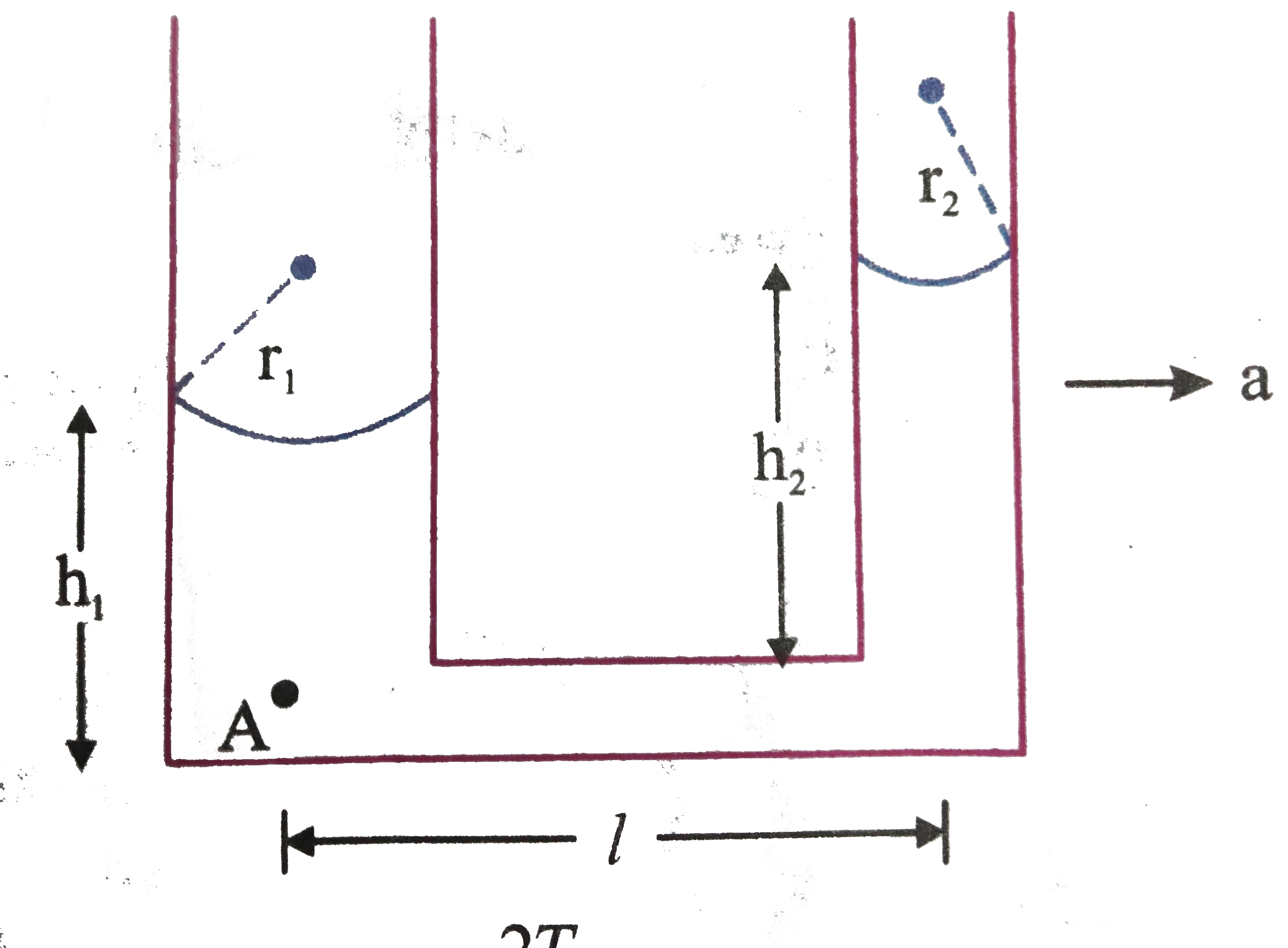
A vertical communicating tube contains a liquid of density `rho`. If it moves with a horizontal acceleration `a`, pressure at `A` is equal to :02:56View SolutionA wooden stick of length `L`, radius `R` and density `rho` has a small metal piece of mass `m` ( of negligible volume) attached to its one end. Find the minimum value for the mass `m` (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density `sigma(gtrho)`.
09:39View SolutionThere are two large identical open tanks as shown in figure. In tanks 1 there is a small hole of cross sectional area A at its base. Tank II has a similar hole, to which a pipe of length h has been connected as shown. The internal cross sectional area of the pipe can be considered to be equal
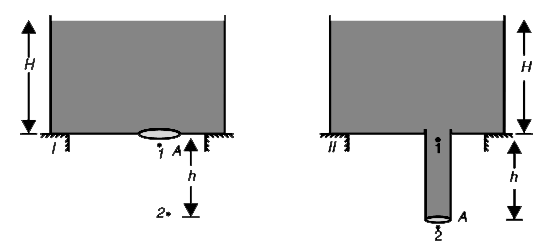
to A. Point 1 marked in both figures, is a point just below the opening in the tank and point 2 marked in both figures, is a point h below point 1 (In fig II, point 2 is just outside the opening in the pipe)
(a) Find the speed of flow at point 2 in both figures.
(b) Find the ratio of speed of flow at point 1 is first the ratio of speed of flow at point 1 is first figure to that in second figure.
(c) Find the difference in pressure at point 1 in both figures.10:31View SolutionA siphon has a uniform circular base of diameter `8//sqrt(pi) cm` with its crest `A, 1.8 m` above the water level vessel `B` is of large cross section (`g= 10 m//s^(2)` and atmospheric pressure `P_(0) = 10^(5) N//m^(2))`.
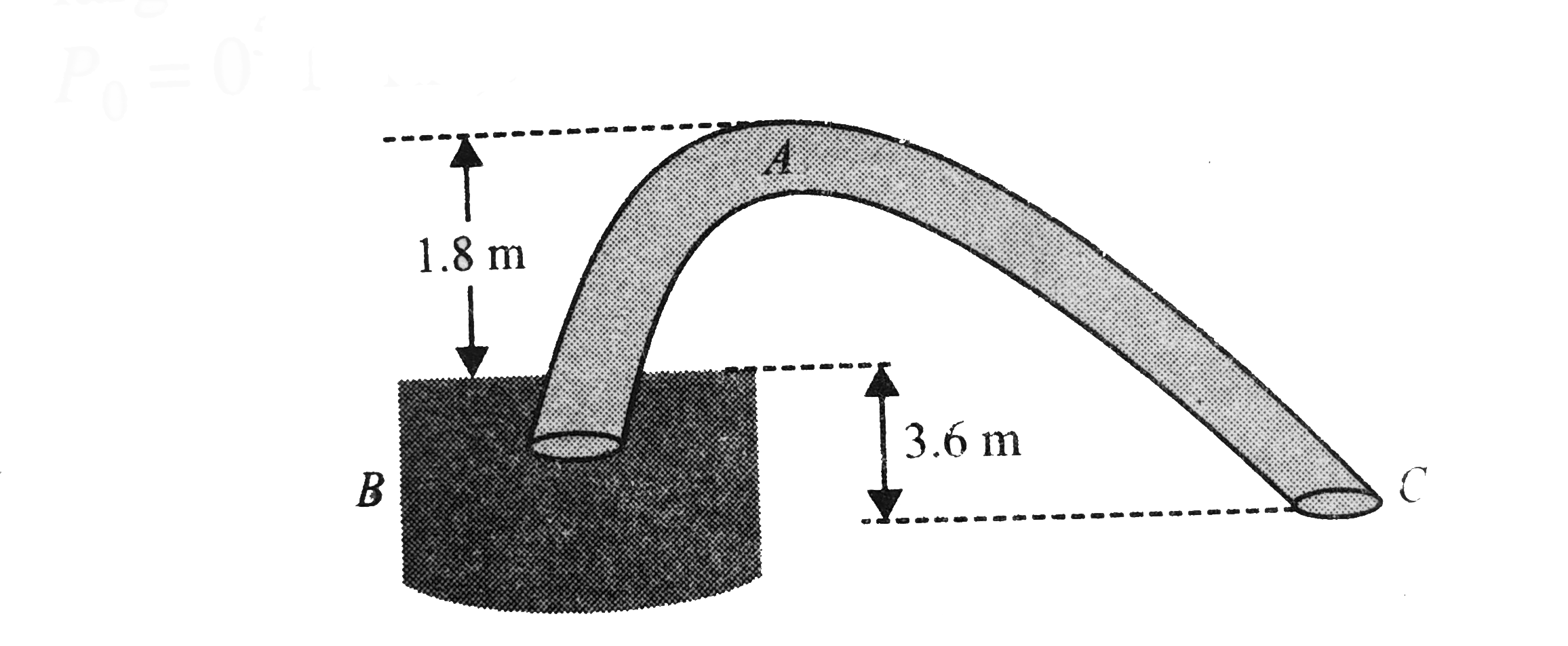 05:12View Solution
05:12View SolutionThere are two large identical open tanks as shown in figure. In tanks 1 there is a small hole of cross sectional area A at its base. Tank II has a similar hole, to which a pipe of length h has been connected as shown. The internal cross sectional area of the pipe can be considered to be equal

to A. Point 1 marked in both figures, is a point just below the opening in the tank and point 2 marked in both figures, is a point h below point 1 (In fig II, point 2 is just outside the opening in the pipe)
(a) Find the speed of flow at point 2 in both figures.
(b) Find the ratio of speed of flow at point 1 is first the ratio of speed of flow at point 1 is first figure to that in second figure.
(c) Find the difference in pressure at point 1 in both figures.10:31View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height `H//2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`. A homogeneous solid cylinder of length `L(LltH//2)` and cross-sectional area `A//5` is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length `L//4` in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area `s(sltltA)` is punched on the vertical side of the container at a height `h(hltH//2)`. As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is04:00View SolutionIn a cylindrical vessel containing liquid of density `rho` there are two holes in the side walls at heights of `h_(1)` and `h_(2)` respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be
 04:49View Solution
04:49View SolutionA large open top container of negligible mass and uniform cross-sectional area `A` has a small hole of croos-sectional area `(A)/(100)` in its side wall near the bottom.The container is kept on a smooth horizontal floor and contains a liquid of density `rho` and mass `m_(0)`. Assuming that the liquid starts flowing out horizontally through the hole at `t = 0`, The acceleration of the container is `(x)/(10) m//s^(2)` than `x` is -
06:52View SolutionA non-viscous liquid of constant density `1000kg//m^3` flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively `4xx10^-3m^2` and `8xx10^-3m^2`. The velocity of the liquid at point P is `1m//s`. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
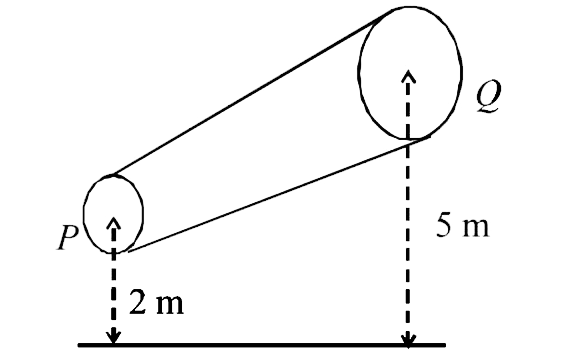 04:41View Solution
04:41View Solution_E01_235_Q01.png)
A cube with mass `m` completely wettable by water floats on the surface of water each side of the cube is `a` what is the distance `h` between the lower face of cube and the surface of the water if surafce tension is S. Take densities of water as `rho_(w)` take angle of contact is zero.05:39View Solution
EXERCISE # II questions and complete solutions for chapter FLUID MECHANICS of BANSAL PHYSICS (HINGLISH) of Class 12
