Complete Solutions to Question Bank of chapter CIRCLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CIRCLES |
| CENGAGE | Question Bank |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
If `a x+b y=10` is the chord of minimum length of the circle `(x-10)^2+(y-20)^2=729` and the chord passes through `(5,15)` then the value of `(4 a+2 b)` is
07:25View SolutionLocus of the poirit of intersection of the pair of perpendicular tangents to the circles `x^2+y^2=1` and `x^2+` `y^2=7` is the director circle of the circle with radius equal to
02:17View SolutionLet `A B` and `C D` are two parallel chords of circle whose radius is 5 units. If `P` and `Q` are mid points of `A B` and `C D` respectively such that `P A . P B=9, Q C . Q D=16`, then distance betweẹn `A B` and `C D` is
05:51View Solutionabout to only mathematics
04:29View SolutionA straight line `l_1` with equation `x-2y+10=0` meets the circle with equation `x^2+y^2=100` at `B` in the first quadrant. A line through `B` perpendicular to `l_1` cuts the y-axis at `P(o,t)` . The value of `t` is 12 (b) 15 (c) 20 (d) 25
05:50View SolutionIf the tangent at the point `P` on the circle `x^2+y^2+6 x+6 y=2` meets the straight line `5 x-2 y+6=0` at a point `Q` on the `y` -axis, then the length of `P Q` is
06:15View SolutionThe radius of the circle whose two normals are represented by the equation `x^2-5 x y-5 x+25 y=0` and which touches externally the circle `x^2+y^2-2 x+4 y-4` `=0` is equal to
06:46View SolutionIf the diagram, `D C` is a diameter of the large circle centered at `A`, and `A C` is a diameter of the smaller circle centered at `B`. If `D E` is tangent to the smaller circle at `F` and `D C=12` then the length of `D E` is
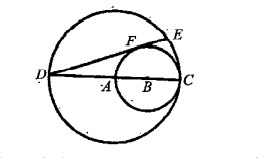 .07:46View Solution
.07:46View SolutionIf `2 x-3 y=0` is the equation of the common chord of the circles, `x^2+y^2+4 x=0` and `x^2+y^2+2 lambda y=0`, then the value of `lambda` is
03:23View SolutionIf one of the diameters of the circle `x^2+y^2-2 x-6 y+6` `=0` is a chord to the circle with centre at `(2,1)` then the radius of the circle is equal to.
05:47View SolutionA circle touches the y-axis at the point (0, 4) and cuts the x-axis in a chord of length 6 units. Then find the radius of the circle.
02:22View SolutionIn the figure given, two circles with centres `C_t` and `C_2` are 35 units apart, i.e. `C_1 C_2=35`. The radii of the circles with centres `C_1` and `C_2` are 12 and 9 respectively. If `P` is the intersection of `C_1 C_2` and a common internal tangent to the circles, then `l(C_1 P)` equals
03:25View SolutionIf the lines `3x-4y+4=0` and `6x-8y-7=0` are tangents to a circle, then find the radius of the circle.
03:39View SolutionThe maximum distance of the point (4,4) from the circle `x^2+y^2-2 x-15=0` is
04:10View SolutionIf the circle `(x-a)^2+y^2=25` intersects the circle `x^2+(y-b)^2=16` in such a way that common chord is of maximum length, then value of `a^2+b^2` is
04:53View SolutionIf a circle `S(x, y)=0` touches at the point `(2,3)` of the line `x+y=5` and `S(1,2)=0`, then `(sqrt2 xx` Radius)` of such circle is
07:42View Solution
Question Bank questions and complete solutions for chapter CIRCLES of CENGAGE of Class 12
