Complete Solutions to Illustrations of chapter GETTING STARTED WITH GRAPHS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GETTING STARTED WITH GRAPHS |
| CENGAGE NEW | Illustrations |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Does the following graph represent a function or a relation?
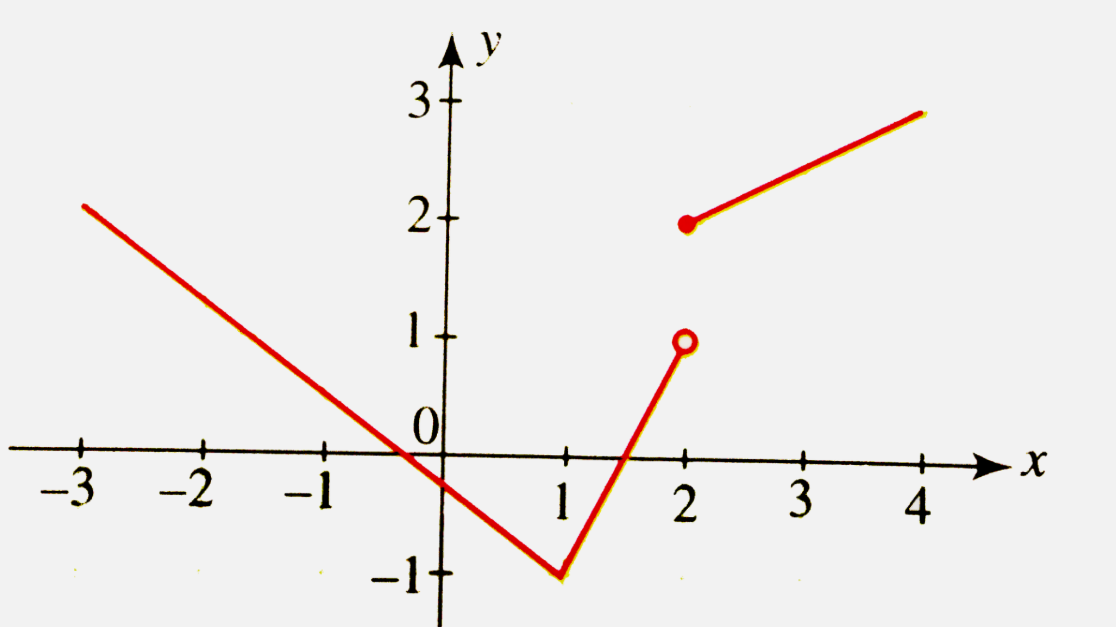 02:11View Solution
02:11View SolutionFind the angle between `vec a and vec b`, when `vec a = hat i +3 hat j + hat k` and `vec b = 2 hat i - hat j - hat k`
02:48View SolutionDoes the following graph pass the vertical or horizontal line test?
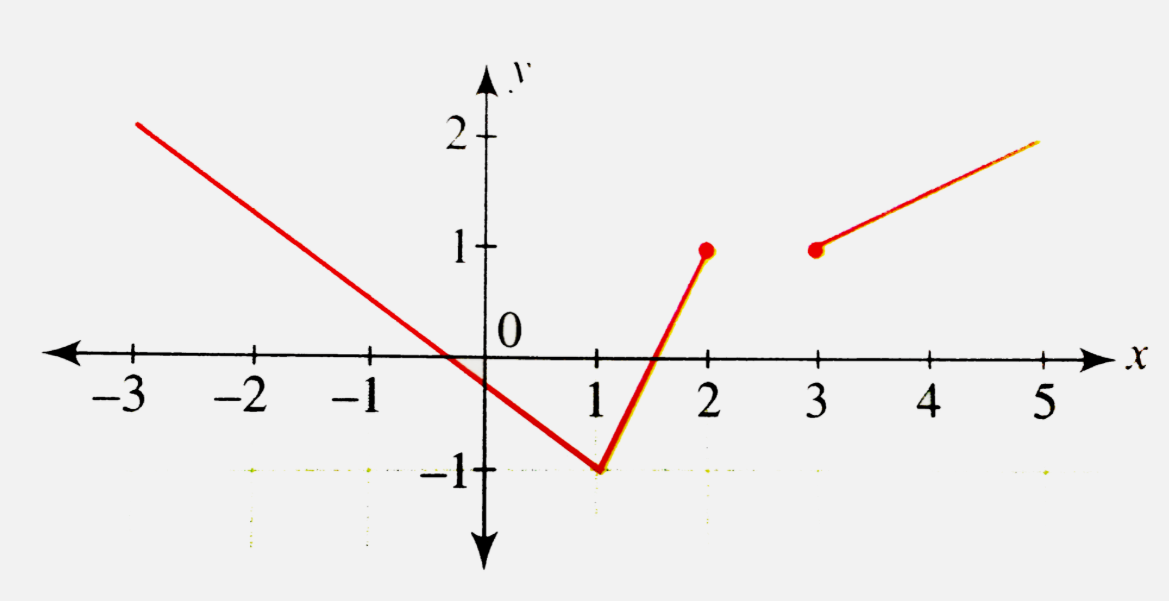 01:45View Solution
01:45View SolutionIn how many points graph of `y=x^3-3x2+5x-3` interest the x-axis?
02:42View SolutionFind the sum of the vectors `vec a = hat i -2 hat j + hat k`, `vec b = 2 hat i +4 hat j +5 hat k` and `vec c = 2 hat i -6 hat j -7 hat k`
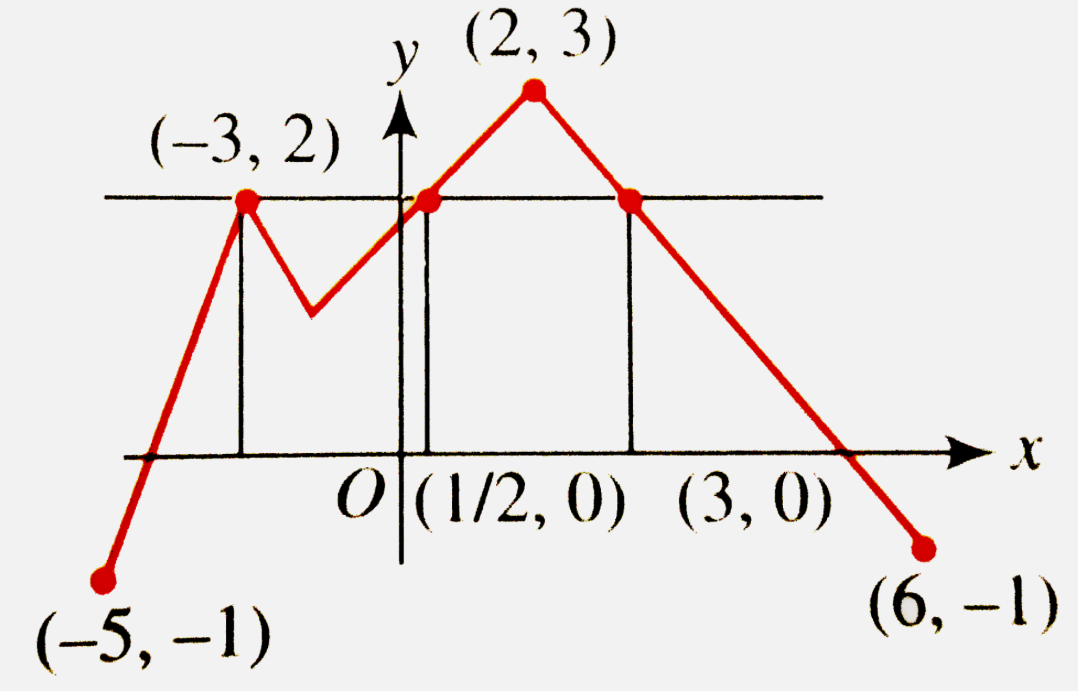
03:03View SolutionWhich of the following pair of graphs intersect? `y=x^2-xa n dy=1` `y=x^2-2x +3 and y=sinx` `y=x^2-x+1a n dy=x-4`
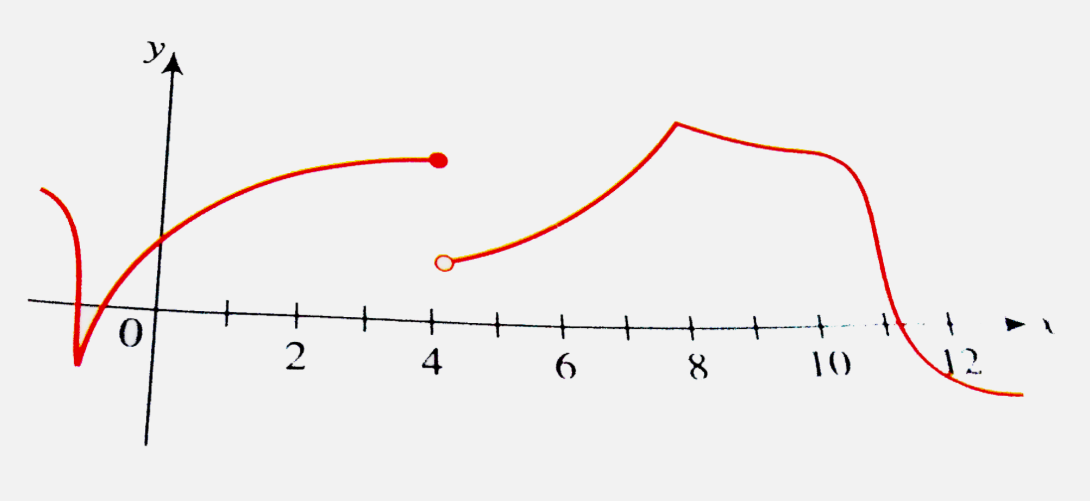
05:24View SolutionThe graph of y = f(x) is shown, find the number of solution of f(f(x)) = 2.
 03:26View Solution
03:26View SolutionDoes the fraph of the function ` f (x) = x^(2) -3` have y - axis symmetry?
01:05View SolutionDoes the graph of the function ` f(x) = 1//x^(3) ` have origin symmetry?
01:41View SolutionWhich of the following functions has (have) y-symmetry or origin symmetry?
(i) ` f(x) = x^(2) sin x" "(ii) f(x) = log (x+sqrt(1+x^(2)))`
(iii)` f(x) = (e^(x)+e^(-x))/2" "(iv) f(x) = {{:(0", ""If x is rational "),(1", " "If x is irrational"):}`04:38View SolutionLet `f: R->R` be a continuous onto function satisfying `f(x)+f(-x)=0AAx in Rdot` If `f(-3)=2a n df(5)=4in[-5,5],` then the minimum number of roots of the equation `f(x)=0` is
03:32View Solutionabout to only mathematics
02:57View SolutionIf the lines `x−2y−6=0,3x+y−4=0 ` and `λx+4y+λ^2=0 ` can be concurrent , then
06:12View SolutionDraw the graph of ` f(x) = {{:(x-2n," "2n le xlt 2n +1),(" where "n in Z." Is "f(x)),(1/2," "2n+1 le x lt 2n+2):}`
periodic? If yes, what is its period?03:08View SolutionIf ` f:R^+→R^+` and ` g:R^+→R^+` , defined as ` f(x)=x^2,g(x)= sqrtx` , then find ` gof` and ` fog` whether are they equivalent?
02:25View SolutionThe graph of ` y = f(x)` is as shown in the following figure.
` (##CEN_GRA_C01_S01_016_Q01.png" width="80%">
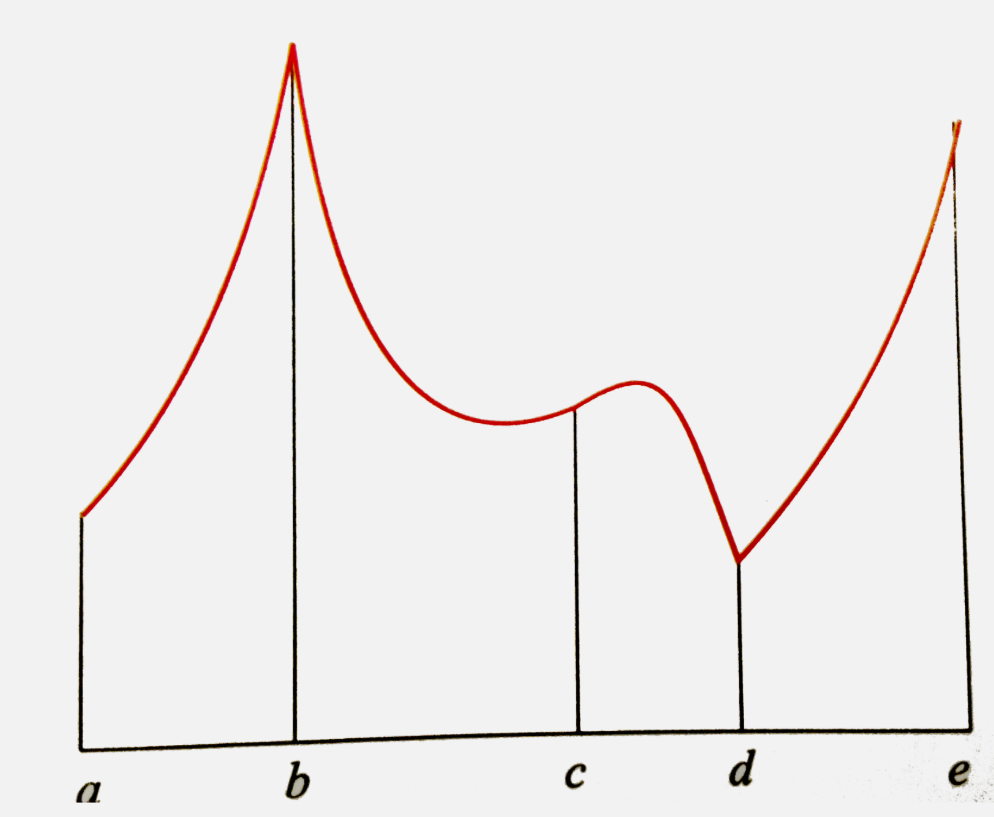
Identify the points of discontinuity and give the reason for the same.View SolutionThe graph of f(x) is given. State with reasons the number at which the function is non-differentiable.
 03:16View Solution
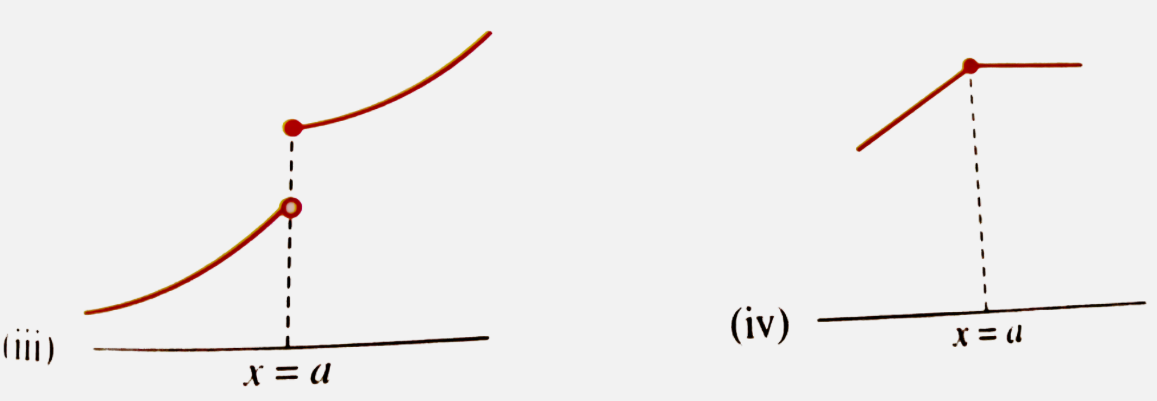
03:16View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
` (##CEN_GRA_C01_S01_018_Q01.png" width="80%">
 02:45View Solution
02:45View SolutionThe graph of a function is shown in the following figure.
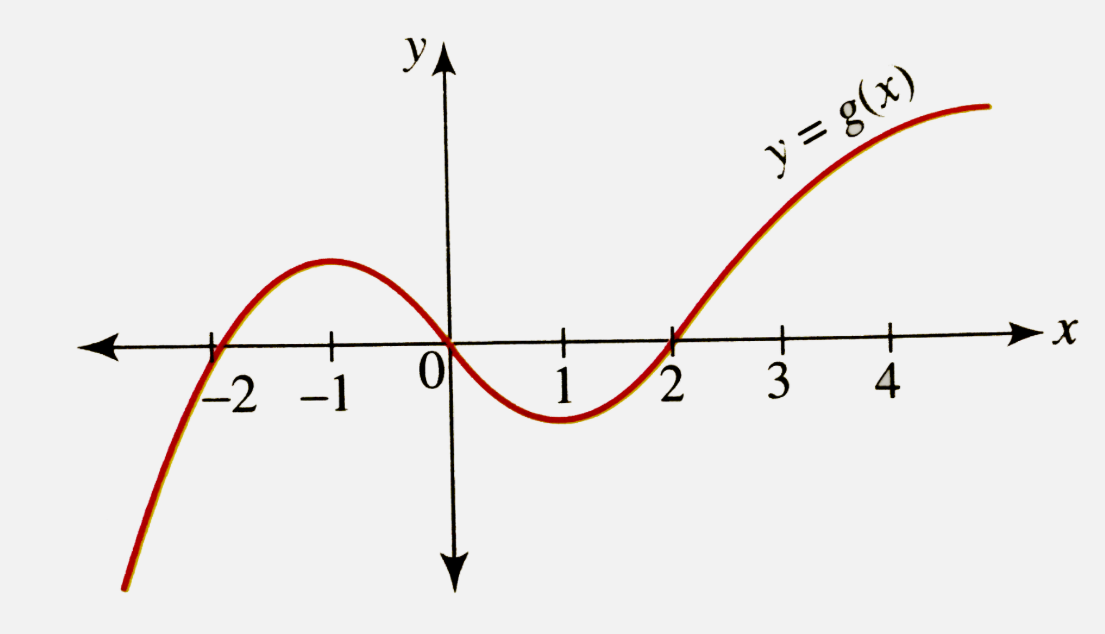
Determine the intervals on which the function is concave up and the intervals on which it is concave down. Find the x - coordinates of any inflection points.03:45View SolutionFor the function g whose graph is given. Arrange the following numbers in increasing order and explain your reasoning.
`g(0), g'(-2), g'(0), g'(2), g'(4)`
 03:26View Solution
03:26View SolutionThe diagram shows the graph of the derivative of a functin f(x) for ` 0 le x le 4 ` with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(a) Tangent line to y = f(x) at x = 0 makes an angle of ` sec^(-1) sqrt 5` with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
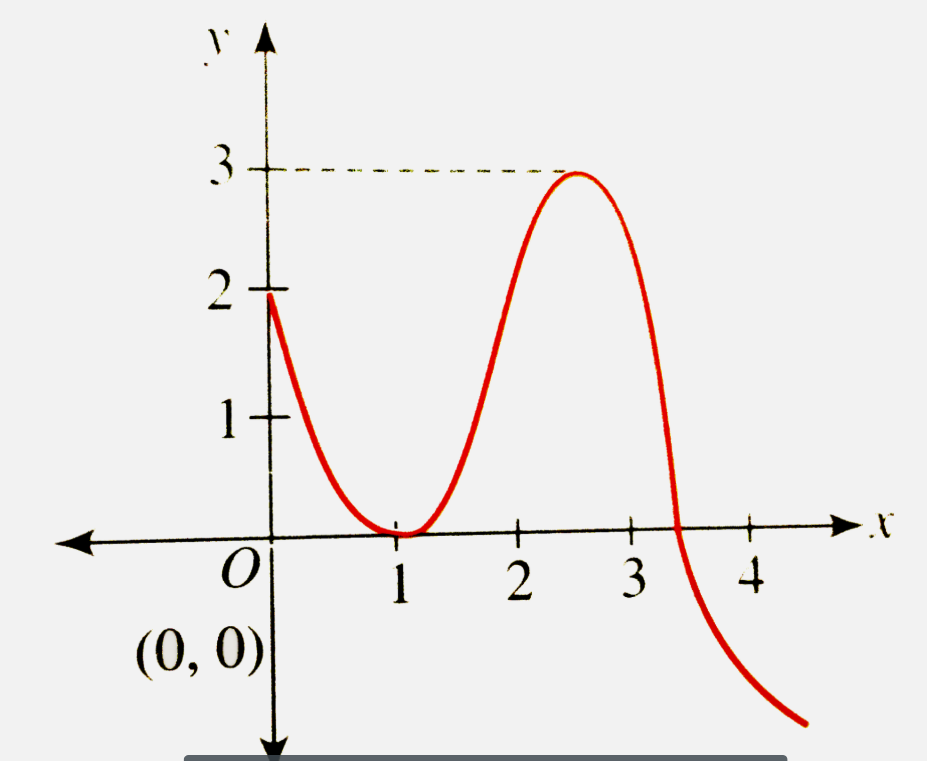
(d) Number of critical point on y = f(x) is two.06:16View SolutionIn the following graph, state the absolute and local maximum and minimum values of the function.
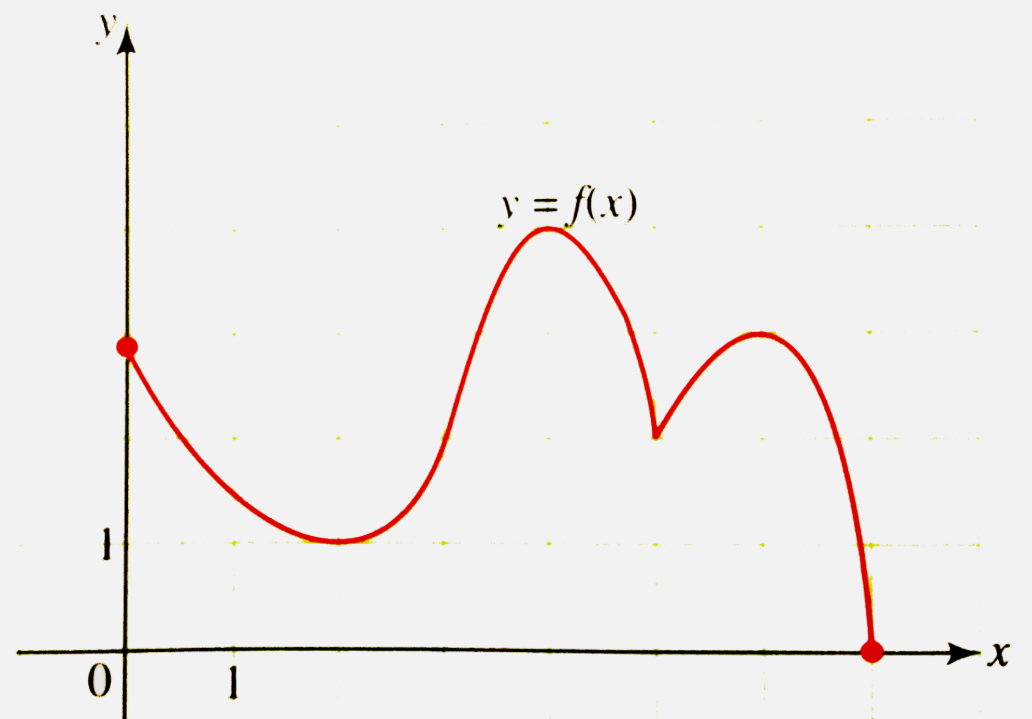 04:10View Solution
04:10View SolutionEvaluate `int (2x-5)^2 dx`
01:50View SolutionThe graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
` (##CEN_GRA_C01_S01_024_Q01.png" width="80%">View SolutionIf `P(E) = 0.10`, what is the probability of not `E`?
02:04View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, ` a le x le b`.
(c) How many points of inflection the graph of ` y = f(x), a le x le b`, has?
(d) Find the points of local maxima/minima of` y = f(x), a lt x b`.
(e) How many roots equation ` f''(x) = 0` has?
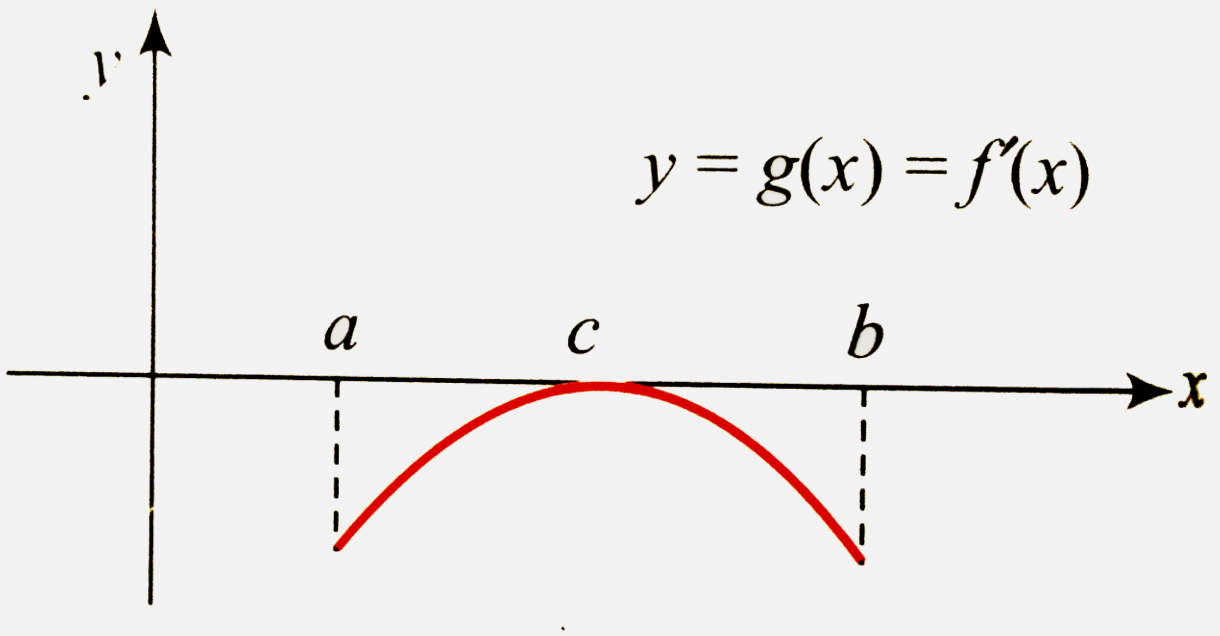 05:11View Solution
05:11View SolutionFind the asymptote of the function ` y = (2x^(2) + 3x + 1)/ x` if any.
04:02View SolutionFind the horizontal, vertical and oblique asymptotes of each of the curves.
`{:((a),y=x/(x+4),,(b),y=(x^(2)+4)/(x^(2)-1)),((c),y=x^(3)/(x^(2)+3x-10),,(d),y=(x^(3)+1)/(x^(3)+x)),((e),y=x/(root(4)(x^(4)+1)),,(f),y=(x-9)/(sqrt(4x^(2)+3x+2))),((g),y=1/(2^(x)-1),,(h),y=1/(log_(e) x)),((i),y= 1/(2^(x) - 1),,,):}`View Solution
Illustrations questions and complete solutions for chapter GETTING STARTED WITH GRAPHS of CENGAGE of Class 12
