Complete Solutions to Examples of chapter SET THEORY AND REAL NUMBER SYSTEM of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | SET THEORY AND REAL NUMBER SYSTEM |
| CENGAGE NEW | Examples |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
State which of the following statement are true and which ones are false . Justify your answer .
(i) `21 in {x|x ` has exactly four positive factors }
(ii) `64 in {y| ` the sun of the all the positve factors of y is 2y }
(iii) `2 in { x |x^4- 3x^3+4x^2-5x+6=0}`
(iv) 23562 `in {y|y ` is divisible by 9}06:58View SolutionAre the following pairs of sets equal ? (i) A={x | x is prime factor of 6 } B={x |x is a solution of `x^2 - 5x + 6 = 0 } Mlbtr` (ii) A={x|y is a letter in the word REPLACED}, B= { y is a letter in the word PARCELED } (iii) A= { x| x is a natural number `x gt 1}` B= {x|x is natural number `x ge 1}`
05:17View SolutionDetermine whether the statement is true or false. If it is true, prove it. If ir false, give an example.
If A`cancel(subset)`B and B`cancel(subset)`C, then A`cancel(subset)`C03:07View SolutionIf `x in A " and " A cancelsub B, " then " x in B`. Is this statement true ?
02:10View SolutionConsider the following sets:
A= set ofnaturai numbers which are multiples of 2
B= set ofnaturai numbers which are multiples of 3
C= set ofnaturai numbers which are multiples of 5
Then find the following set
`(i) A cup B (ii) B cup C (iii) A- B (iv) B-C (v)A cap C
(vi) A cap B cap C (vii) ( A cup B )- C`08:37View SolutionIf A- B = A and B- A=B , then what can we consclude ?
08:37View SolutionIf ` A cap B = A cup B` then what can we conclude ?
01:24View SolutionShow that `A ∩ B = A ∩ C` need not imply `B = C`.
02:49View SolutionConsider the following sets:
A = set all rectangles in the same plane
B = set all squares in the same plane
C = set all parellegrams in the same plane
Find the following sets : `(i) A-B (ii) C-A (iii) A cap C (iv) B cap C (v) B cup C (Vi ) A cap B cup C `05:19View SolutionShow that if `A ⊂ B`, then `C – B ⊂ C – A`.
03:06View SolutionAssume that `P ( A ) = P ( B )`. Show that `A = B`
04:55View SolutionIf sets A= (-3,2) and B= (-1, 5) then find the following sets :
04:35View SolutionIn a group of 500 people, 350 speak Hindi and 300 speak English. It is given that each person speaks at least one language.
(i) How many people can speak both Hindi and English?
(ii) How many people can speak Hindi only?
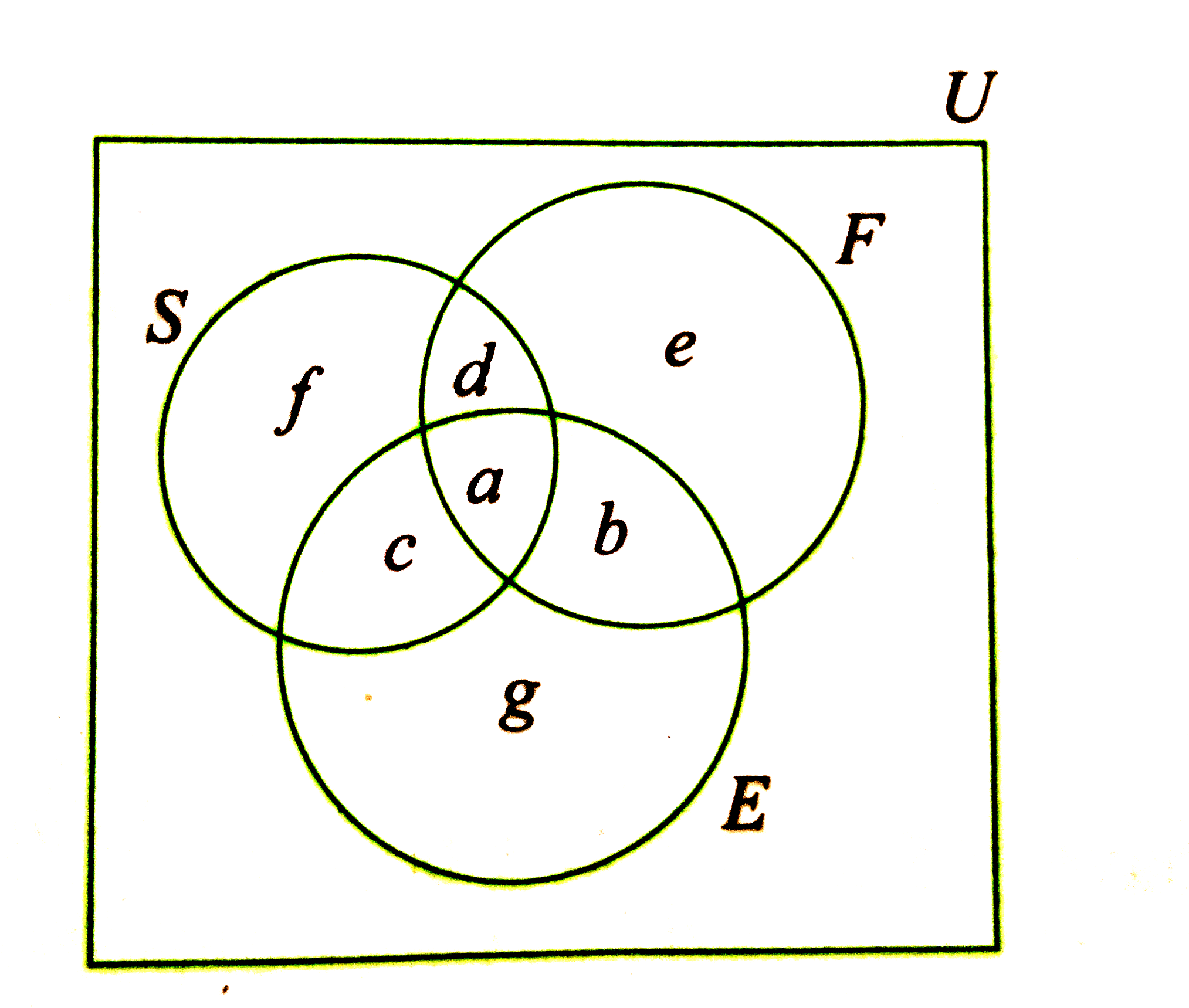
(iii) How many people can speak English only?05:53View SolutionIn a group of 50 students, the number of students learning - French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15, French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who are learning at?
French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
(ix) exactly one language (X) exactly two languages
 14:02View Solution
14:02View SolutionSolve the following inequlaities ,Write the solution in the from of intervals (i) `3x ge 18`
(ii) `2x + 17 lt 3`
`(iii) 7- 4x gt -17 `
(iv)` x/7+3 le -2`View SolutionSolve the following inequlaities
` 7x +15 ge 9 - 4x `
`-5 le ""(2-3x)/(4) le 9`
`5x- 6 le 4 " and " 7- 3x ge 2x`07:24View SolutionAbhinav obtained 65 and 80 marks in first two unit test .Find the minimum marks he should get in the third test of have an average of at least 70 marks.
03:19View SolutionSolve `sqrt((x-5))-sqrt(9-x)>0,x in Zdot`
00:59View SolutionSolve `sqrt(x-2)geq-1.`
01:53View SolutionSolve `sqrt(x-1)>sqrt(3-x)dot`
02:29View SolutionSolve `x sqrt(x ) ge sqrt( x )-3`
01:15View SolutionFind the value of `x^(2)` for the given values of x.
`(i) x lt 3 (ii) x gt -1 (iii) x ge 2 (iv) x lt -1`02:16View SolutionFind all the possible the value of the following expression`dot` `sqrt(x^2-4)` (ii) `sqrt(9-x^2)` (iii) `sqrt(x^2-2x+10)`
03:12View SolutionSolve `(x^2-4)sqrt(x^2-1)<0.`
03:33View SolutionFind the values of 1/x for the given values of x.
`(i) x gt 3 (ii) x lt -2 (iii) x in (-1, 3) -{0}`02:23View SolutionFind all possible values of the following expressions :
`(i) (1)/(x^(2)+2) (ii) (1)/(x^(2)-2x +3) (iii) (1)/(x^(2)-x-1)`03:17View SolutionSolve `x^2-x-2> 0.`
02:08View SolutionSolve `x^2-x-1 lt 0`
02:54View SolutionSolve `(x-1)(x-2)(1-2x)> 0.`
02:11View SolutionSolve `2/x gt 3 `
01:45View SolutionSolve `(x-2)/(x+2) gt (2x-3)/(4x-1)`.
02:05View SolutionSolve `x >sqrt((1-x))dot`
02:53View SolutionSolve `2/(x^2-x+1)-1/(x+1)-2/(x^3+1)geq0.`
04:59View SolutionSolve `x(x+2)^2(x-1)^5(2x-3)(x-3)^4geq0.`
03:30View SolutionSolve `x(2^x-1)^(3^x-9)^5(x-3)<0.`
03:18View SolutionSolve `(x^2-x-1)(x^2-x-7)<-5.`
03:19View SolutionSolve the following :
(i) `|x| = 5`
(ii) `x^2- |x|-2 =0 `02:35View SolutionFind the value of `x` for which following expressions are defined: `1/(sqrt(x-|x|))` (ii) `1/(sqrt(x+|x|))`
03:35View SolutionFind all the possible values of following expressions :
(i) ` ( |x|)/(x) + (|y|)/y `
(ii) `|x|/x+|y|/y+|z|/z`03:44View SolutionSolve `|x|=x^2-1.`
02:23View Solution(i) For ` 2 lt x lt 4,` find the values of `|x|`.
(ii) For `-3 le x le -1` find the values of `|x|`.
(iii) For `-3 le x le 1,` find the values of `|x|`.
(iv) For `-5 lt x lt 7,` find the values of ` |x-2|`.
(iv) For `1 le x le 5,` find the values of `|2x-7|.`01:53View SolutionSolve `|x-2|=1`
01:01View SolutionFind the values of `a` for which the equation `||x-2|+a|=4` can have four distinct real solutions.
02:05View SolutionSolve the following :
(i) `|x-2|=(x-2) " (ii) " |x+3| = -x-3`
(iii) `|x^(2)-x|=x^(2)-x " (iv) " |x^(2)-x-2| =2+x-x^(2)`02:06View SolutionSolve `1-x=sqrt(x^2-2+1.)`
02:20View SolutionSolve `|3x-2|=xdot`
02:02View SolutionSolve `sqrt(x+3-4sqrt(x-1))+sqrt(x+8-6sqrt(x-1))=1`
04:50View SolutionProve that `sqrt(x^2+2x+1)-sqrt(x^2-2x+1)`= `{-2 , x<-1, 2x, -1lt=xlt=1 2, x >1}`
06:59View SolutionFor `x in R ,` find all possible values of `|x-3|-2` (ii) `4-|2x+3|`
02:10View SolutionFind the possible values of `sqrt(|x|-2)` (ii) `sqrt(3-|x-1|)` (iii) `sqrt(4-sqrt(x^2))`
05:01View SolutionSolve `|x-3|+|x-2|=1.`
03:06View SolutionSolve `x^2-4|x|+3<0.`
02:33View SolutionSolve `0 lt |x| lt 2`
01:40View SolutionSolve `|3x-2|<4.`
02:05View SolutionSolve `1 le |x-2| le 3`
02:30View SolutionSolve `0 lt | x-3| le 5`
02:56View SolutionSolve `|| x-1|-2 | lt 5 `
02:51View SolutionSolve `|x-3|geq2.`
02:05View Solution`||x| -3| gt 1.`
02:13View SolutionSolve `|(x-3)/(x+1)|lt=1.`
02:46View SolutionSolve `|1+3/x|>2`
04:22View SolutionSolve `|x|+|x-2|=2.`
02:35View SolutionSolve `|2x-3|+|x-1|=|x-2|dot`
05:17View SolutionSolve `x^2+x-4|=|x^2-4|+|x|dot`
02:40View SolutionIf `|s in x+cos x|=|s in x|+|cos x|(s in x ,cos x!=0)` , then in which quadrant foes `x` lie?
02:03View SolutionIs `|t a n x+cos x|<|t a n x|+|cot x|` true for any `x ?` If it is true, then find the values of `xdot`
02:31View SolutionSolve `|(x+1)/x|+|x+1|=((x+1)^2)/(|x|)dot`
02:23View SolutionSolve `|x^2-2x|+|x-4|<|x^2-3x+4|dot`
02:37View SolutionSolve `|2^x-1|+|4-2^x|<3.`
04:25View SolutionFind the total number of integer `n` such that `2lt=nlt=2000` and H.C.F. of `n` and 36 is 1.
04:18View SolutionIf A = {b, c, e, g, h}, B = {a, c, d, g, i} and C = {a, d, e, g, h}, then show that `A-(BcapC)=(A-B)cup(A-C)`.
03:05View SolutionFor sets A,B, and C using Venn diagram , check if A-(B-C) = (A-B-C)
06:56View SolutionSuppose `A_1,A_2….. A_(30)` are thirty sets each having 5 elements and `B_1B_2…..B_n` are n sets each having 3 elements ,Let `overset(30)underset(i=1)bigcupA_1=overset(n)underset(j=1)bigcupB_j=s`
and each element of S belongs to exactly 10 of the `A_1` and exactly 9 of the value of n.03:25View SolutionLet `a >2` be a constant. If there are just 18 positive integers satisfying the inequality `(x-a)(x-2a)(x-a^2)<0,` then find the value of `adot`
07:21View SolutionFind the set of all possible real value of a such that the inequality `(x-(a-1))(x-(a^2+2))<0` holds for all `x in (-1,3)dot`
04:04View SolutionFind all possible values of `(x^2+1)/(x^2-2)` .
02:55View SolutionSolve `(1/3)^((|x+2|)/(2-|x|))> 9.`
04:23View SolutionSolve `|x-1|+|x-2|geq4.`
02:37View SolutionSolve `|x+1|+|2x-3|=4.`
02:40View SolutionSolve `(x)/(x+2) le (1)/(|x|)`
03:55View Solution
Examples questions and complete solutions for chapter SET THEORY AND REAL NUMBER SYSTEM of CENGAGE of Class 12
