Complete Solutions to Exercise of chapter GRAPHS OF ELEMENTARY FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GRAPHS OF ELEMENTARY FUNCTIONS |
| CENGAGE NEW | Exercise |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Draw the graph of `y= (1)/((1//x))`.
01:13View Solution(a) Draw the graph of `f(x) = ={{:(1",",, |x| ge 1), ((1)/(n^(2)) ",",, (1)/(n)lt |x|lt (1)/(n-1)","n= 2"," 3"," ...), (0",",, x=0):}`
(b) Sketch the region `y le -1`.
(c) Sketch the region `|x| lt 3`.02:49View SolutionSketch the regions which points satisfy `|x+y| ge 2`.
03:38View SolutionSketch the region satisfying `|x| lt |y|`.
04:15View SolutionLet `f:R→R:f(x)=(x+1)` and `g:R→R:g(x)=(x^2−2)`. Write down the formulae for `(gof)`.
02:15View SolutionDraw the graph of `y= (x-1)/(x-2)`.
03:59View SolutionThe following figure shows the graph of `f(x) =ax^(2)+bx +c`, then find the sign of values of `a, b and c`.
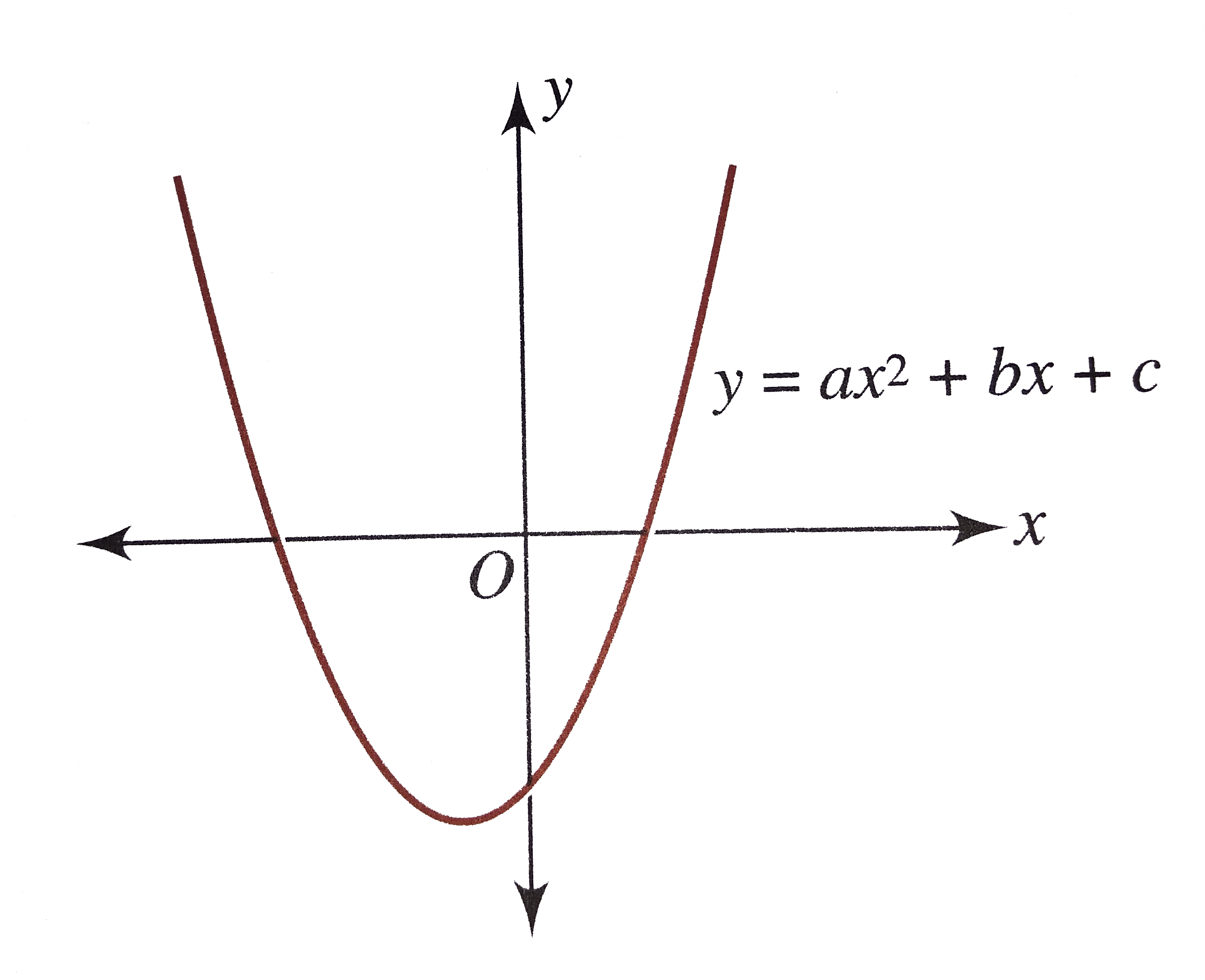 01:30View Solution
01:30View SolutionThe entire graph of the equation `y=x^2+k x-x+9` in strictly above the `x-a xi s` if and only if `k<7` (b) `-5-5` (d) none of these
02:51View SolutionIf `x^2+2a x+a<0AAx in [1,3],` the find the values of `adot`
05:25View SolutionDraw the graph of `f(x) = x|x|`.
02:40View SolutionDraw the graph of the function: Solve `|(x^2)/(x-1)|lt=1` using the graphical method.
04:56View SolutionDraw the graph of `y = |x^(2) - 2x|-x`.
02:50View SolutionDraw the graph of `y =2^(x)"," x^(2)-2x le 0 `
02:25View SolutionFind the roots of the equation by factorization: `2x^2-x-1`
03:08View SolutionDivide `16(x^2yz + xy^2z+xyz^2)` by `4xyz`
01:47View SolutionFind the set of real value(s) of `a` for which the equation `|2x+3|+2x-3|=a x+6` has more than two solutions.
04:44View SolutionDraw the graph of `y=|x|`.
01:39View SolutionDraw the graph of `y=1/(log_(e)x)`
03:55View SolutionFind the number of real solutions to the equation `log_(0.5)x=|x|`.
02:22View SolutionDraw the graph of `f(x)= x+ [x]`, where `[*]` denotes the greatest integer function.
02:48View SolutionGiven `f(x)` is a periodic function with period 2 and it is defined as
`" "f(x) = {{:([cos""(pix)/(2)]+1",",,0lt x lt 1), (2-x",",,1 le x lt 2):}`
Here `[*]` represents the greatest integer `le x`. If `f(0)=1`, then draw the graph of the function for `x in [-2, 2]`.03:37View SolutionSketch the region of relation `[x] + [y] = 5, x, y ge 0`, where `[*]` denots the greatest integer function.
02:55View SolutionDraw the graph of `y= 2^({x})`, where `{*}` represents the fractional part function.
02:38View SolutionLet `f(x) = ([x]+1)/({x}+1) ` for `f: [0, (5)/(2) ) to ((1)/(2) , 3]`, where `[*]` represents the greatest integer function and `{*}` represents the fractional part of x.
Draw the graph of `y= f(x)`. Prove that `y=f(x)` is bijective. Also find the range of the function.02:36View SolutionDraw the graph of `y= 2^({x})`, where `{*}` represents the fractional part function.
02:38View SolutionFind tha area of the region containing the points `(x, y)` satisfying `4 le x^(2) + y^(2) le 2 (|x|+ |y|)`.
04:01View SolutionDraw the graph of `y= sqrt (x^(2)-1)`
02:02View SolutionDraw the graph of `y=|x|^(1/2)` for `-1lt=x<1.`
03:20View SolutionDraw the graph of `f(x) = "sgn"(log _(e) x)`.
01:07View SolutionDraw the graph of `y= x-sinx`
01:59View SolutionDraw the graph of the function `y= f(x) = lim_(n to oo) (x^(2n)-1)/(x^(2n)+1)`. Is this function same as the function `g(x) = "sgn"(x^(2)-1)`.
02:33View SolutionAn even periodic function `f:R to R ` with period 4 is such that
`f(x)={{:(max.(|x|, x^(2))",",, 0lex lt1), (x",",,1le xle 2):}`. Then draw the graph of `y= f(x)` for `x in R`03:31View SolutionIF the domain of the function `f(x) =x^2 -6x +7` is `(-oo , oo)` then range of the function is
04:03View SolutionSolve `sin^(-1)xlecos^(-1)x` graphically. Check the differentiability of f (x) =min. `{sin^(-1)xlecos^(-1)x}`. Also find the range of y = f(x)
01:19View Solution
Exercise questions and complete solutions for chapter GRAPHS OF ELEMENTARY FUNCTIONS of CENGAGE of Class 12
