Complete Solutions to Illustrations of chapter GRAPHS OF ELEMENTARY FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GRAPHS OF ELEMENTARY FUNCTIONS |
| CENGAGE NEW | Illustrations |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
The graph of `(y-x)` against `(y+x)` is shown below.
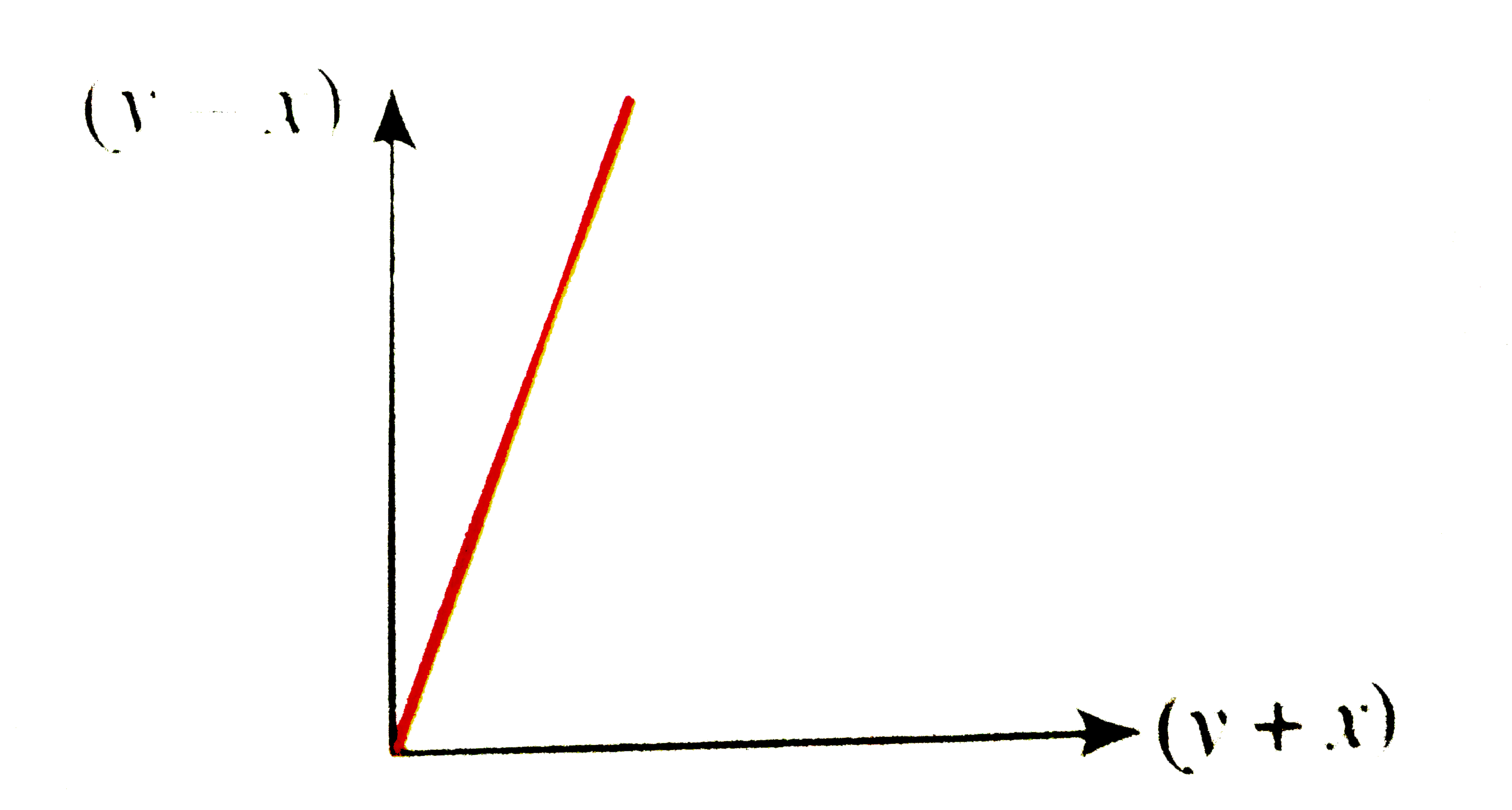
Which one of the following shows the graph of `y` against `x` ?
 05:06View Solution
05:06View SolutionDraw the graph of `f(x)=(x^(2)-8x+15)/(x^(2)-2x)`.
03:12View SolutionIn the given figure, the value of x is
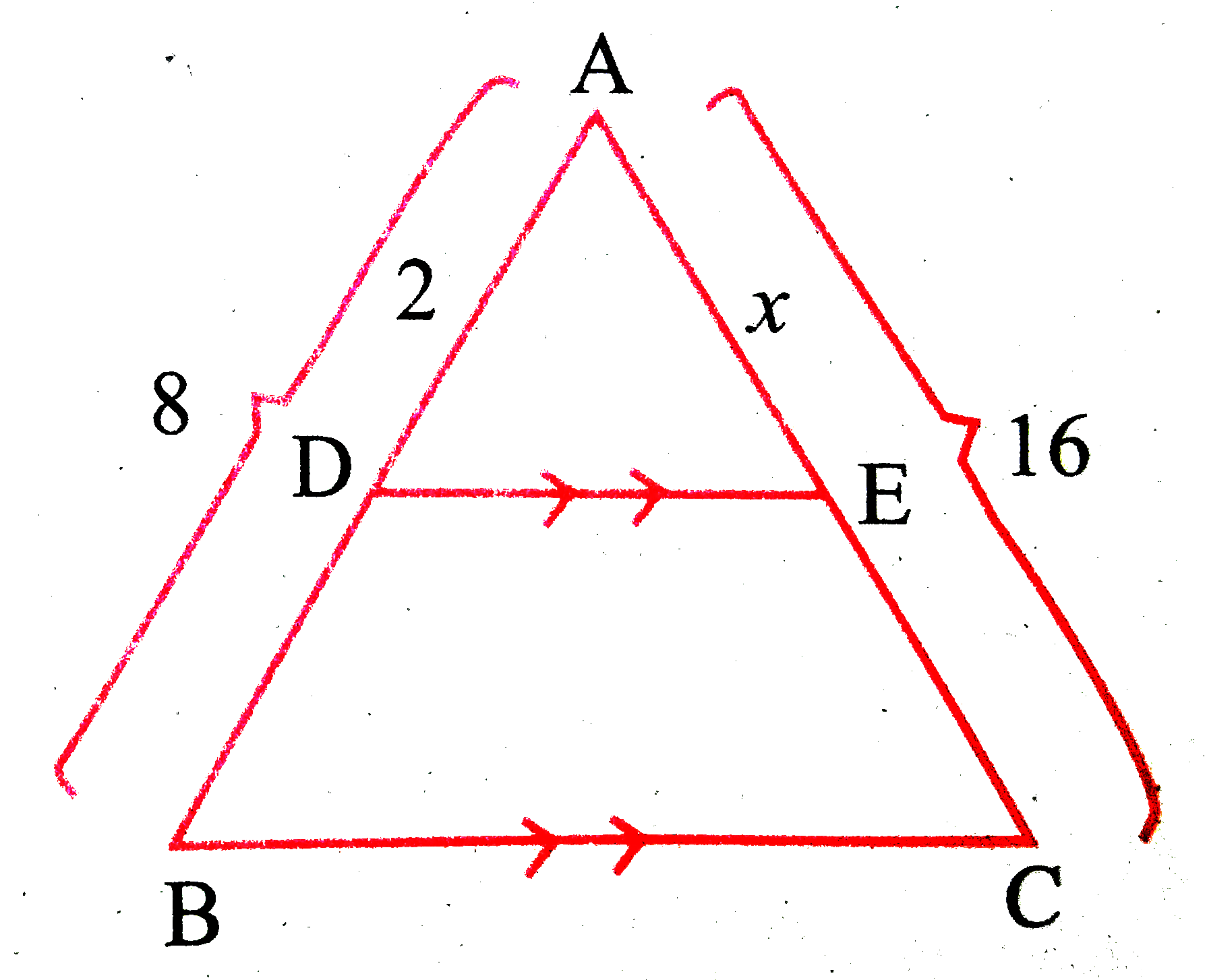 01:44View Solution
01:44View SolutionLet `f((x+y)/2)=(f(x)+f(y))/2fora l lr e a lxa n dy` If `f^(prime)(0)` exists and equals `-1a n df(0)=1,t h e n f i n d f(2)dot`
06:08View SolutionSketch the regions satisfying the following inequalities:
(a) `x gt 2`
(b) `|y| ge 1`03:53View SolutionShade the regions where points satisfy `|x-y| lt 1`.
04:50View SolutionPlot the region satisfying `|x|+ |y| le 2 and |x|+|y| gt 2`.
03:49View SolutionIf `x lt 2`, then find the values of `x^(2)` graphically.
01:24View SolutionIf `x lt -1`, then find the vallues of `x^(2)` graphically.
02:11View SolutionDraw the graph of `f(x) = {{:(x^(3)","x^(2) lt 1), (x","x^(2)le1):}`
03:32View SolutionIf `x gt 2`, then find the values of `1//x` graphically.
01:21View SolutionIf `x lt -1`, then find the values of `1//x` graphically.
01:33View SolutionWhen `x gt -2`, find the values of `1//x`.
02:05View SolutionWhen `x lt 3`, find the values of `1//x`.
01:55View SolutionDraw the graph of `(1)/(x)+ (1)/(y)=1`.
04:13View SolutionDraw the graph of `y=(1)/(x^(2))`.
02:05View SolutionDraw the graphs of (i) `y=x^(2)-x-6` (ii) `y=6-x-x^(2)` and find zeroes in each case.
What do you notice ?07:53View SolutionThe following figure shows the graph of `f(x)= ax^(2)+ bx+c`, find the sign of `a, b and c`.
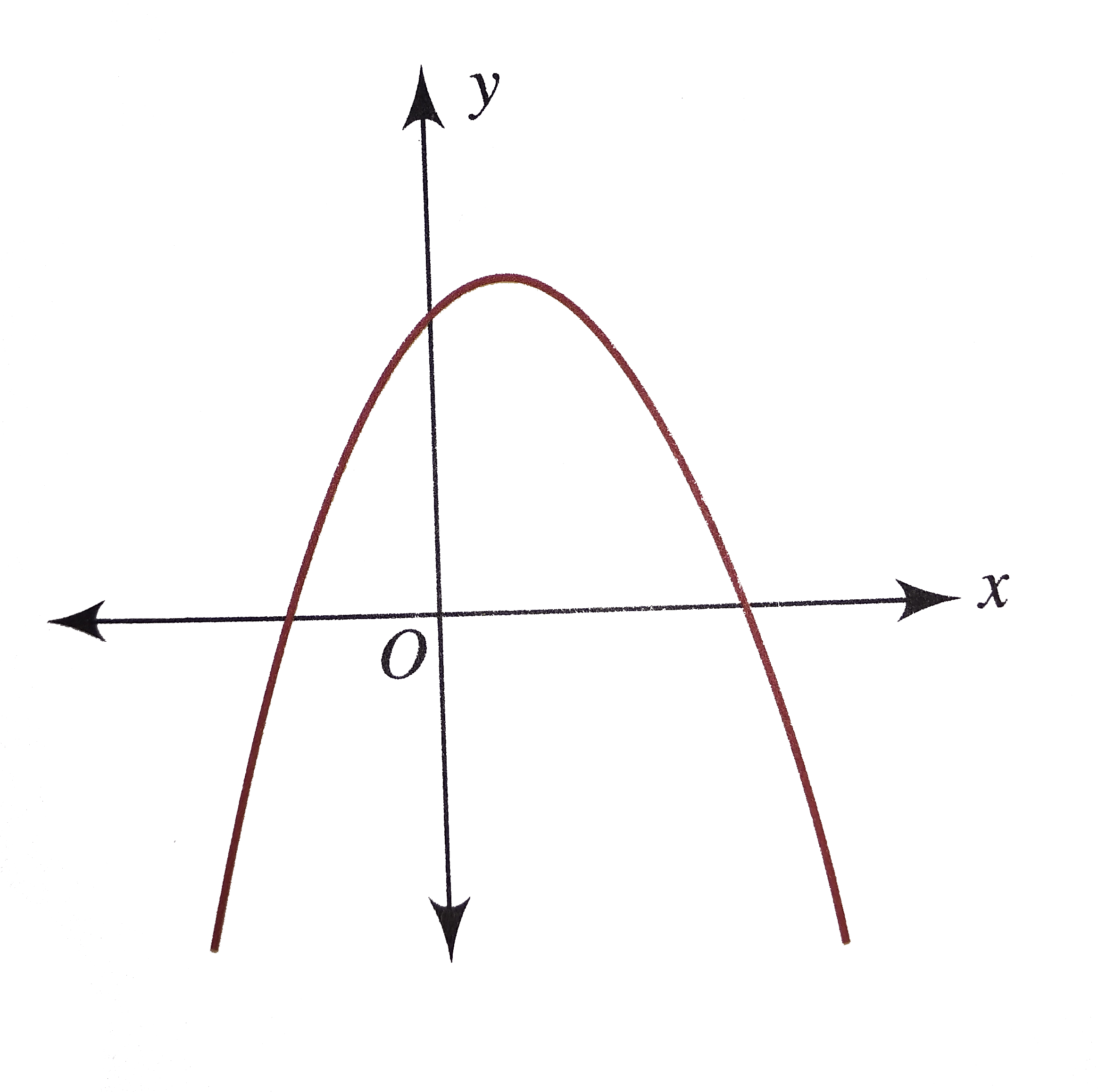 05:30View Solution
05:30View SolutionLet `f(x)=2x(2-x), 0 le x le 2`. Then find the number of solutions of `f(f(f(x)))= (x)/(2)`.
04:33View SolutionIf `f(x) = {{:(kx , "for ". x le 2),(3, "for " x gt 2):}` is continuous at x=2 then the value of k is ………………………. .
02:43View SolutionIf `f(x)=x^3+4x^2+lambdax+1` is a monotonically decreasing function of `x` in the largest possible interval `(-2,-2/3)dot` Then `lambda=4` (b) `lambda=2` `lambda=-1` (d) `lambda` has no real value
02:39View SolutionFor what real values of `a` do the roots of the equation `x^2-2x-(a^2-1)=0` lie between the roots of the equation `x^2-2(a+1)x+a(a-1)=0.`
05:32View SolutionFind the value of `a` for which `a x^2+(a-3)x+1<0` for at least one positive real `x` .
06:45View SolutionConsider the inequality, `9^(x)-a.3^(x)-a+3 le 0`, where `'a'` is a real parameter.
(a) Find the value of `'a'` for which the inequality has at least one negative solution.
(b) Find the values of `'a'` for which the inequality has at least one positive solution.
(c) Find the vlaues of `'a'` for which the inequality has at least one real solution.03:50View SolutionLet a, b, c real. If `ax^(2)+bx+c=0` has two real roots `alpha and beta,` where `alpha lt -1and betagt1,` then show that `1+c/a+|(b)/(a)|lt0`
02:19View SolutionIf `b gt a,` then the equation `(x-a)(x-b)-1=0` has
03:11View SolutionWhen `x gt -2`, find the values of `|x|` graphically.
01:42View SolutionWhen `x gt -2`, find the values of `|x|` graphically.
01:42View SolutionIf |x + 2| `le` 9 , then x belongs to
01:54View SolutionDraw the graph of `f(x) = x|x|`.
02:40View SolutionDraw the graph of `y=|x|`.
01:39View SolutionDraw the graph of `f(x) = x|x|`.
02:40View SolutionDraw the graph of the function `f(x)= x- |x-x^(2)|, -1 le x le 1` and find the points of non-differentiability.
03:22View SolutionThe set of all real numbers x for which `x^(2)-|x+2|+ x gt0` is
02:44View SolutionDraw the graph of `f(x)= |x|-|2x-3|`. Find the range of the function.
03:40View SolutionDraw the graph of `f(x) = x|x|`.
02:40View SolutionLet `f(x)=x+2|x+1|+x-1|dotIff(x)=k` has exactly one real solution, then the value of `k` is 3 (b) 0 (c) 1 (d) 2
04:59View Solution`L e tf(x)={x^3+x^2+3x+sinx|(3+s in1/x ,),x!=0. 0x=0` then the number of point where `f(x)` attains its minimum value is_____
02:52View SolutionThe tangent to the curve `y=e^x` drawn at the point `(c,e^c)` intersects the line joining `(c-1,e^(c-1)) and (c+1,e^(c+1))` (a) on the left of `x=c` (b) on the right of `x=c` (c) at no points (d) at all points
09:03View SolutionIf a continous founction of defined on the real line R, assumes positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum values is negative, then the equation `f(x)=0` has a root in R. Considetr `f(x)=ke^(x)-x` for all real x where k is real constant.
The line y=x meets `y=ke^(x)"for" k le0` at04:54View SolutionIf a continous founction of defined on the real line R, assumes positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum values is negative, then the equation `f(x)=0` has a root in R. Considetr `f(x)=ke^(x)-x` for all real x where k is real constant.
The line y=x meets `y=ke^(x)"for" k le0` at04:54View SolutionIf a continous founction of defined on the real line R, assumes positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum values is negative, then the equation `f(x)=0` has a root in R. Considetr `f(x)=ke^(x)-x` for all real x where k is real constant.
The line y=x meets `y=ke^(x)"for" k le0` at04:54View SolutionFind the number of solutions of equation `2^x+3^x+4^x-5^x=0`
02:15View SolutionDraw the graph of `y= log_(x)sqrtx`
01:10View SolutionFind number of roots of the equation ` x^(3)-log_(0.5) x = 0`.
03:41View SolutionThe circles `x^2+y^2-12 x-12 y=0` and `x^2+y^2+6x+6y=0.` touch each other externally touch each other internally intersect at two points none of these
02:59View SolutionDraw the graph of `f(x) = x|x|`.
02:40View SolutionDraw the graph of the function `f(x)=x^2
02:51View SolutionDraw the graph of `f(x) = [x^(2)], x in [0, 2)`, where `[*]` denotes the greatest integer function.
02:55View SolutionDraw the graph of `f(x)= [sqrtx], x in [0, 16)`, where `[*]` denotes the greatest ineger function.
02:30View SolutionDraw the graph of `y= [x]+ sqrt(x-[x])`, where`[*]` denotes the greatest ineger function.
04:09View SolutionDraw the graph of `f(x) = [log_(e)x], e^(-2) lt x lt 10`, where `[*]` represents the greatest integer function.
04:22View SolutionSolve `x^2-4-[x]=0` (where `[]` denotes the greatest integer function).
04:48View SolutionSketch the region of relation `[x] + [y] = 5, x, y ge 0`, where `[*]` denots the greatest integer function.
02:55View SolutionDraw the graph of `f(x) ={2x}`, where `{*}` represents the fractional part function.
03:02View SolutionFind the domain of `f(x) = sqrt (|x|-{x})` (where `{*}` denots the fractional part of x).
03:14View SolutionSolve : `x^(2) = {x}`, where `{x}` represents the fractional part function.
02:45View SolutionDraw the graph of `y= 2^({x})`, where `{*}` represents the fractional part function.
02:38View SolutionDraw the graph of `y =(1)/({x})`, where `{*}` denotes the fractional part function.
01:39View SolutionSolve : `4{x}= x+ [x]`(where `[*]` denotes the greatest integer function and `{*}` denotes the fractional part function.
02:00View SolutionGiven the graph of the function `y=f(x)`, draw the graph of `y ="sgn"f(x)`.
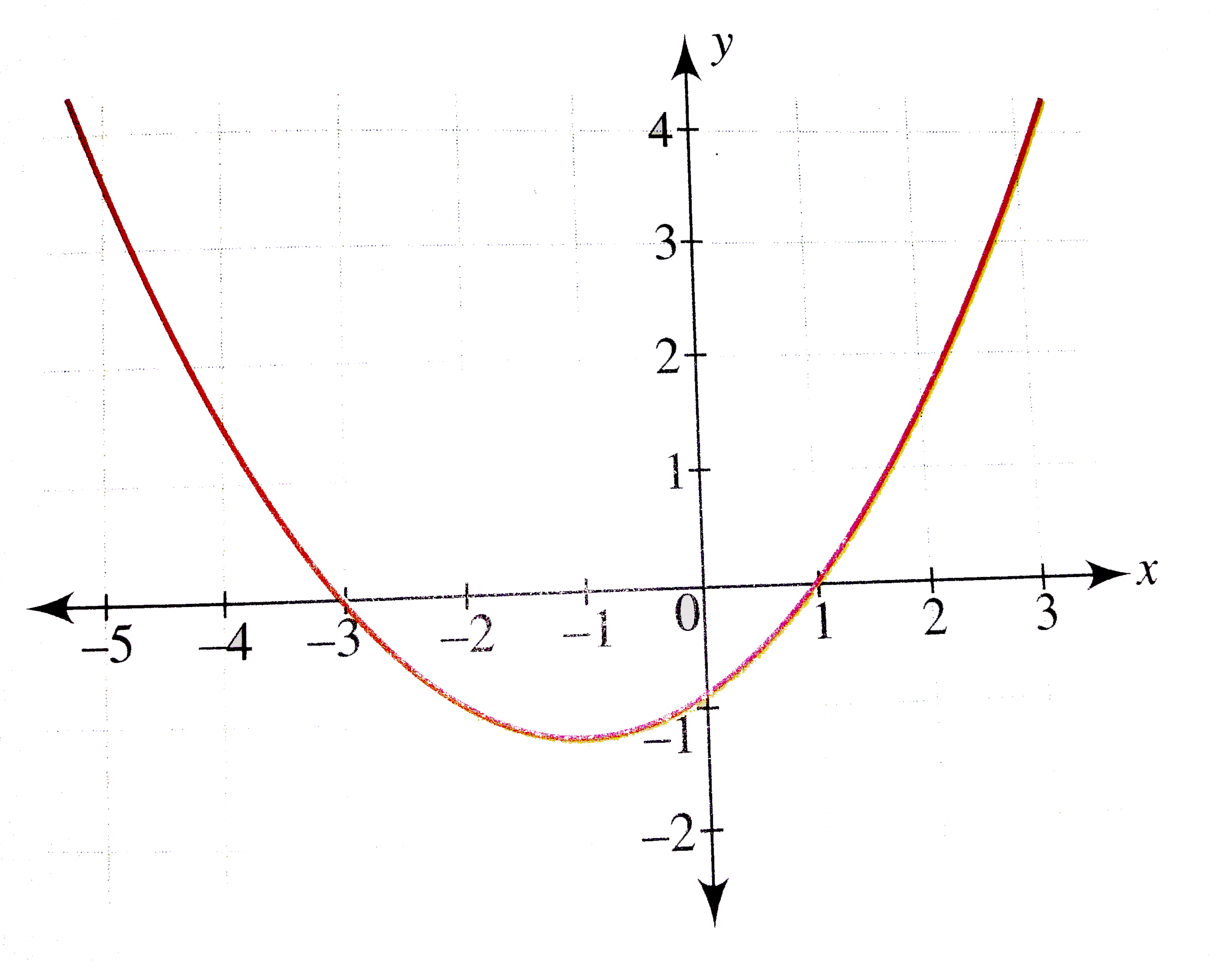 02:30View Solution
02:30View SolutionDraw the graph of `f(x) = "sgn"(x^(3) -x)`.
03:26View SolutionDraw the graph of `f(x) = "sgn"(log _(e) x)`.
01:07View SolutionLet a function `f(x)` be defined in `[-2, 2]` as
`f(x) = {{:({x}",",, -2 le xlt -1), (|"sgn "x|",",,-1le x le 1),({-x}",",, 1 lt xle 2):}` where `{x}` and sgn `x` denote fractional part and signum functions, respectively. Then find the area bounded by the graph of `f(x)` an the x-axis.02:20View SolutionLet `f: R to R ` be defined as `f(x) = e^("sgn "x)+ e^(x^(2))`. Then find the range of the function, and also indentify the type of the function : one-one or many-one.
03:46View SolutionDraw the graph of the function `f(x) = max. {x, x^(2)}` and write its equivalent definition.
04:29View SolutionLet `f : R to R ` be a function defined by `f(x) = max. {x, x^(3)}`. The set of all points where `f(x) ` is NOT differenctiable is
(a) `{-1, 1}`
(b) `{-1, 0}`
(c ) `{0, 1}`
(d) ` {-1, 0, 1}`01:52View SolutionFind the equivalent definition of `f(x)=m a xdot{x^2,(-x)^2,2x(1-x)}w h r e0lt=xlt=1`
06:31View SolutionLet `f:R-> R and g:R-> R` be respectively given by `f(x) = |x| +1 and g(x) = x^2 + 1`. Define `h:R-> R` by `h(x)={max{f(x), g(x)}, if xleq 0 and min{f(x), g(x)}, if x > 0`.The number of points at which `h(x)` is not differentiable is
02:43View SolutionPlot the region of the points P (x,y) satisfying `|x|+|y| lt 1.`
04:51View SolutionConsider the regions `A= {(x, y)|x^(2) + y^(2) le 100 } and B = {(x, y) |sin (x+y) gt 0}` in the plane. Then find the area of the region `A uu B`.
04:32View SolutionDraw the graphs of the following parabolas :
(i) `x=y ^(2) - 2y -3`
(ii) `x = 6+y -y^(2)`05:37View SolutionFind the number of roots of equation `xsinx=1`
03:56View SolutionLet `g(x)=sqrt(x-2k),AA2klt=x<2(k+1),` where `k in ` integer. Check whether `g(x)` is periodic or not.
04:14View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line `x=3.`
07:43View SolutionDraw the graph of `y= sqrt (x^(2)-1)`
02:02View SolutionDraw the graph of `y= -sqrt (6-3x^(2))`
02:31View SolutionThe eccentricity of the ellipse `9x^2+25 y^2-18 x-100 y-116=0` is `25//16` b. `4//5` c. `16//25` d. `5//4`
03:45View SolutionFind the area enclosed by the curves `y= sqrtx and x= -sqrty` and the circle `x^(2) + y^(2) =2` above the x-axis.
03:12View SolutionPlot the region in the first quadrant in which the points are nearer to the origin thatn to the line `x=3`.
07:43View Solution
Illustrations questions and complete solutions for chapter GRAPHS OF ELEMENTARY FUNCTIONS of CENGAGE of Class 12
