Complete Solutions to Illustrations of chapter GRAPHICAL TRANSFORMATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GRAPHICAL TRANSFORMATIONS |
| CENGAGE NEW | Illustrations |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
Plot `y=|x|,y+x-2|,a n dy=|x|2|`
04:21View SolutionDraw the graph of `y=sin^(-1)(x-3)`.
02:40View SolutionDraw the graph of `y="log"_(e)(x+3)`,
01:39View SolutionDraw the graph of `y=cot^(-1)x+sec^(-1)x+cosec^(-1)x`.
01:52View SolutionDraw the graph of `y=|x-3|+1`.
02:47View SolutionSolve `3x+2ygt12` graphically
02:48View SolutionFor `a le 0,` jdetermine all real roots of the equation
`x^(2)-2a|x-a|-3a^(2)=0`04:16View SolutionConsider the function `f(x)={x-[x]-1/2,ifx !in Io,ifx in I ,w h e r e[dot]` denotes the fractional integral function and `I` is the set of integers. Then find `g(x)=m a xdot{x^2,f(x),|x|;-2lt=xlt=2.`
05:57View SolutionIf `f(x)=2x+1 and g(x)=x^2-2`, then `gof(x)` is
01:27View SolutionFind angle between the vectors ,When`vec a = hat i -2 hat j +3 hat k` and `vec b = 3 hat i -2 hat j + hat k`
03:19View SolutionDraw the graph of `y=0.5(x-1)^(2)` and compare with `y=(x-1)^(2)`.
01:26View SolutionPlot `y=sinxa n dy=sin2xdot`
04:09View SolutionFind fog(x), if f(x)=∣x∣ and g(x)=∣5x−2∣
01:25View SolutionPlot the curve `y=(log)_e(-x)dot`
01:10View SolutionTo draw the graph of y = log e ( − x ) , flip the graph of y = log e x over the y-axis shown in the following figure.
03:55View SolutionFind the value of k for which the equation `x^2 −6x+k=0` has distinct roots.
01:22View SolutionDraw the graph of `y=-cot^(-1)x`.
01:48View SolutionDraw the graph of `y=-log_(e)x`.
01:58View SolutionDraw the graph of `y=2-|x-1|`.
01:35View SolutionDraw the graph of `y=sin^(-1)(cosx)`.
04:49View SolutionGiven the graph of `y=f(x)`.
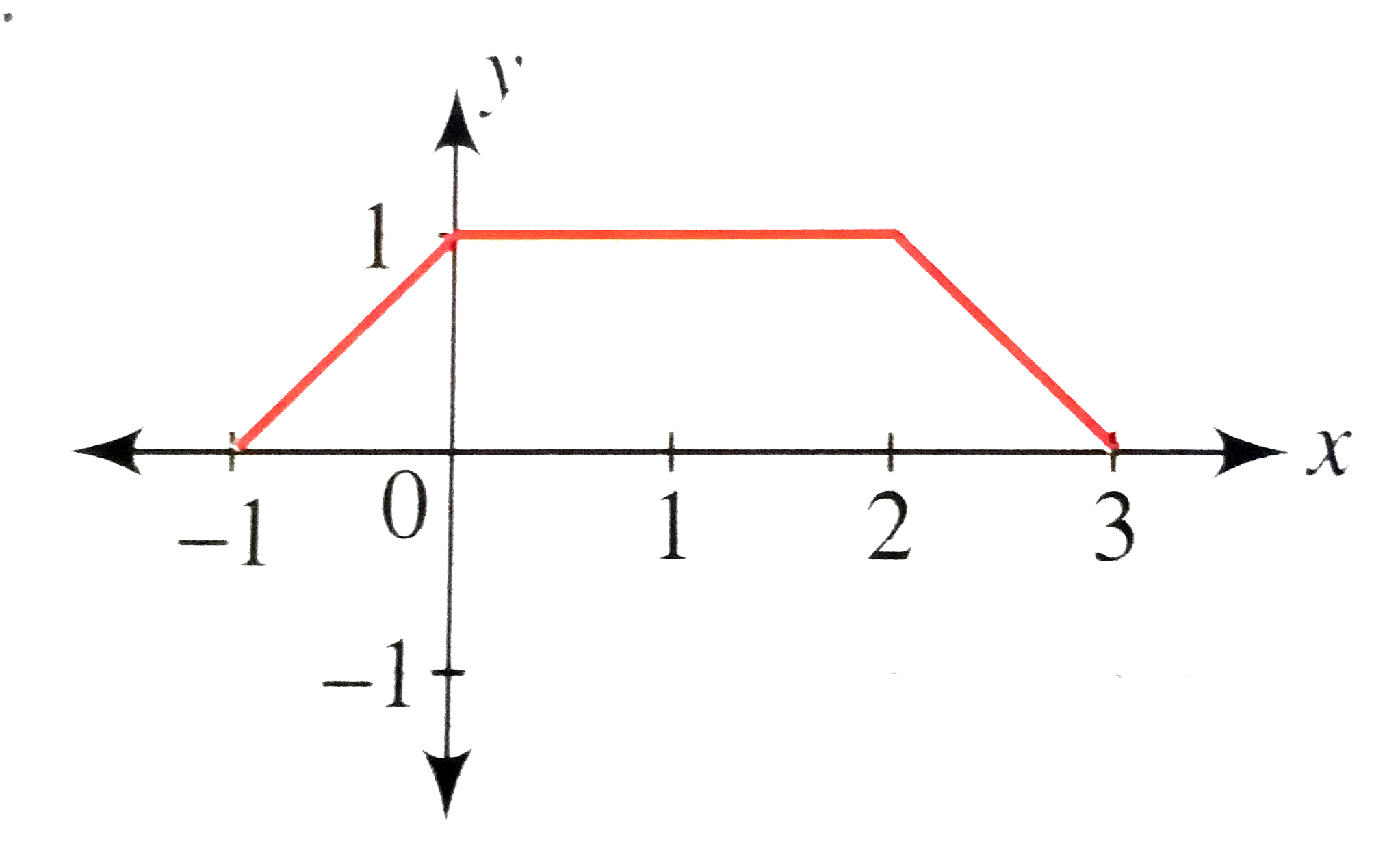
Draw the graphs of the followin.
(a) `y=f(1-x)` (b) `y=-2f(x)`
(c) `y=f(2x)` (d) `y=1-f(x)`View SolutionDraw the graph for `y=|logx|`
03:07View SolutionDraw the graph of `y=|sinx|` and hence the graph of `y=sin^(-1)|sinx|`.
03:12View SolutionDraw the graph of `y=f(x)=sqrt(1-cosx)`
01:33View SolutionDrew the graph of `y=|sinx-0.5|`.
02:23View SolutionThe number of solution of `2cosx=|sinx|` where `x in [0.4pi]` is/are
02:04View SolutionSolve `|x^2+4x+3|+2x+5=0.`
03:39View SolutionSolve `cos 2x gt | sin x|, x in (- pi/2, pi)`
05:05View SolutionProve that the equation `2s in x|x|+a` has not solution for `a in ((3sqrt(3)-pi)/3-oo)dot`
04:26View SolutionSolve `|x^(2)-1|+|x^(2)-4|lt6` graphically.
03:37View SolutionDiscuss the differentiability of `f(x)=mim.{|x|,|x-2|,2-|x-1|}`.
03:05View SolutionIf the equation `|x^2+b x+c|=k` has four real roots, then `b^2-4c >0a n d00a n dk >(4c-b^2)/4` none of these
04:02View SolutionSketch the curve `y="log"|x|`
02:12View SolutionDraw the graph of `y=sin|x|`.
01:42View SolutionDraw the graph of `y=[|x|]`, where `[.]` denotes the greatest integer function.
02:43View SolutionDraw the graph of `y=sin^(-1)|x|`.
01:41View SolutionDraw the graph of `y=tan^(-1)|x|`.
01:09View SolutionDraw the graph of `y={|x|}`, where `{.}` represents the fractional part function.
01:49View SolutionDraw the graph of the function: `f(x)=|x^2-3|x|+2|`
03:58View SolutionDraw the graph of `y=|1-(1)/(|x|-2)|`.
01:35View SolutionDraw the graph of `|y|=|2^|x|-3|`.
02:35View SolutionFind the total number of solutions to `sinpix=|In|x||`.
02:09View SolutionFind the number of solutions to `7^|x|(|1-|x||)=1`.
02:58View SolutionThe graph of the function `y=f(x)` is shown.
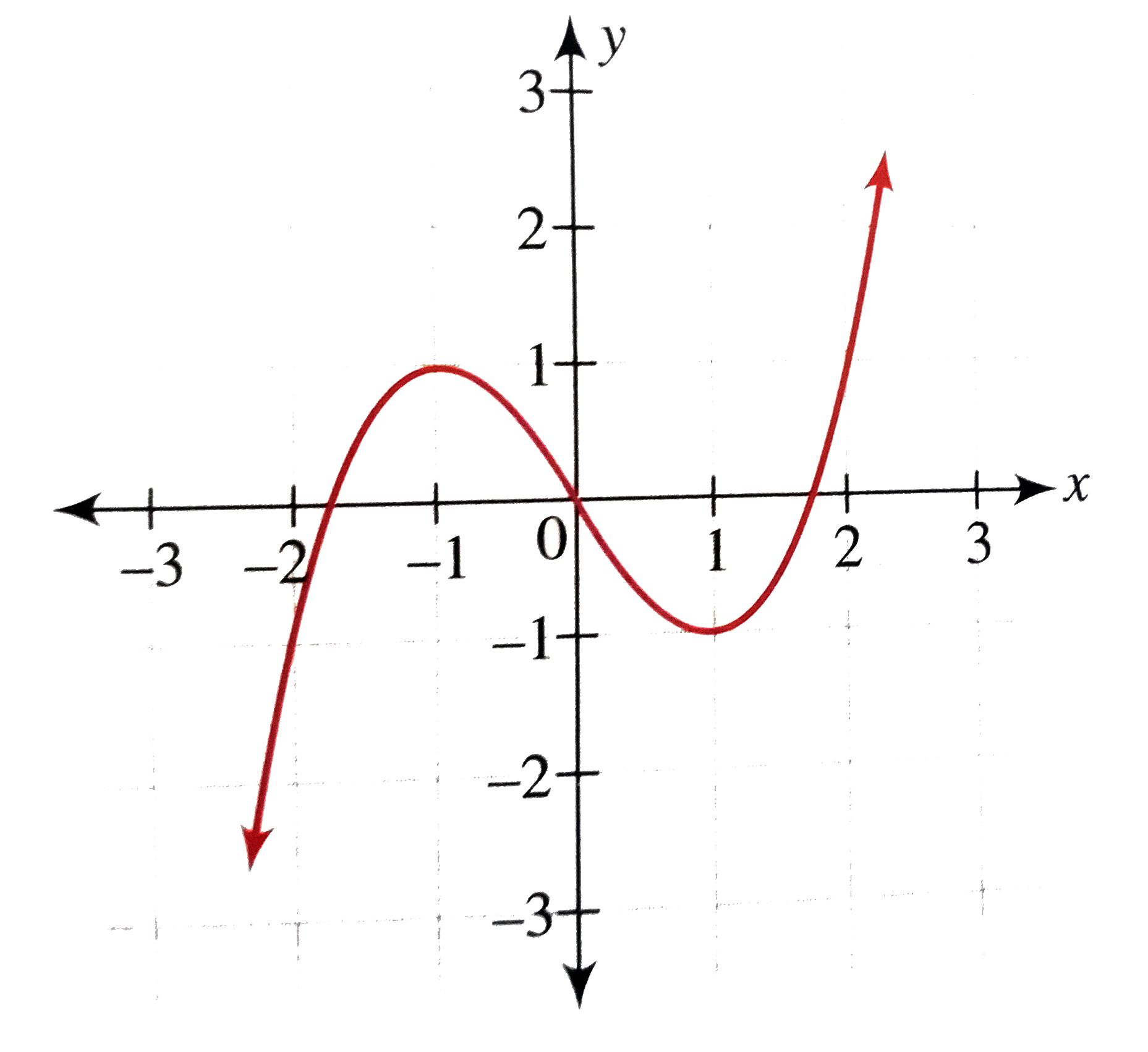
Find the number of solutions to the equation `||f(x)|-1|=(1)/(2)`.View SolutionConsider the function `f(x)=x^(2)+bx+c,` where `D=b^(2)-4cgt0`, then match the follwoing columns.
 02:10View Solution
02:10View SolutionDraw the graph of `|y|=sinx`.
01:19View SolutionDraw the graph of `|y|=tanx`.
01:58View SolutionSketch the curve `|y|=(x-1)(x-2)dot`
03:26View SolutionDraw the graph of `|y|={x}`, where `{.}` represents the fractional part function.
02:02View SolutionDraw the graph of `|x|+|y|=1+x`.
01:28View SolutionDraw the graph of `|x|-|y|=2` using graphical transformation.
01:25View SolutionDraw the graph of `y=|2^(|x|)-3|`.
02:35View SolutionGiven the graph of the function `y=f(x)`, draw the graph of `y ="sgn"f(x)`.
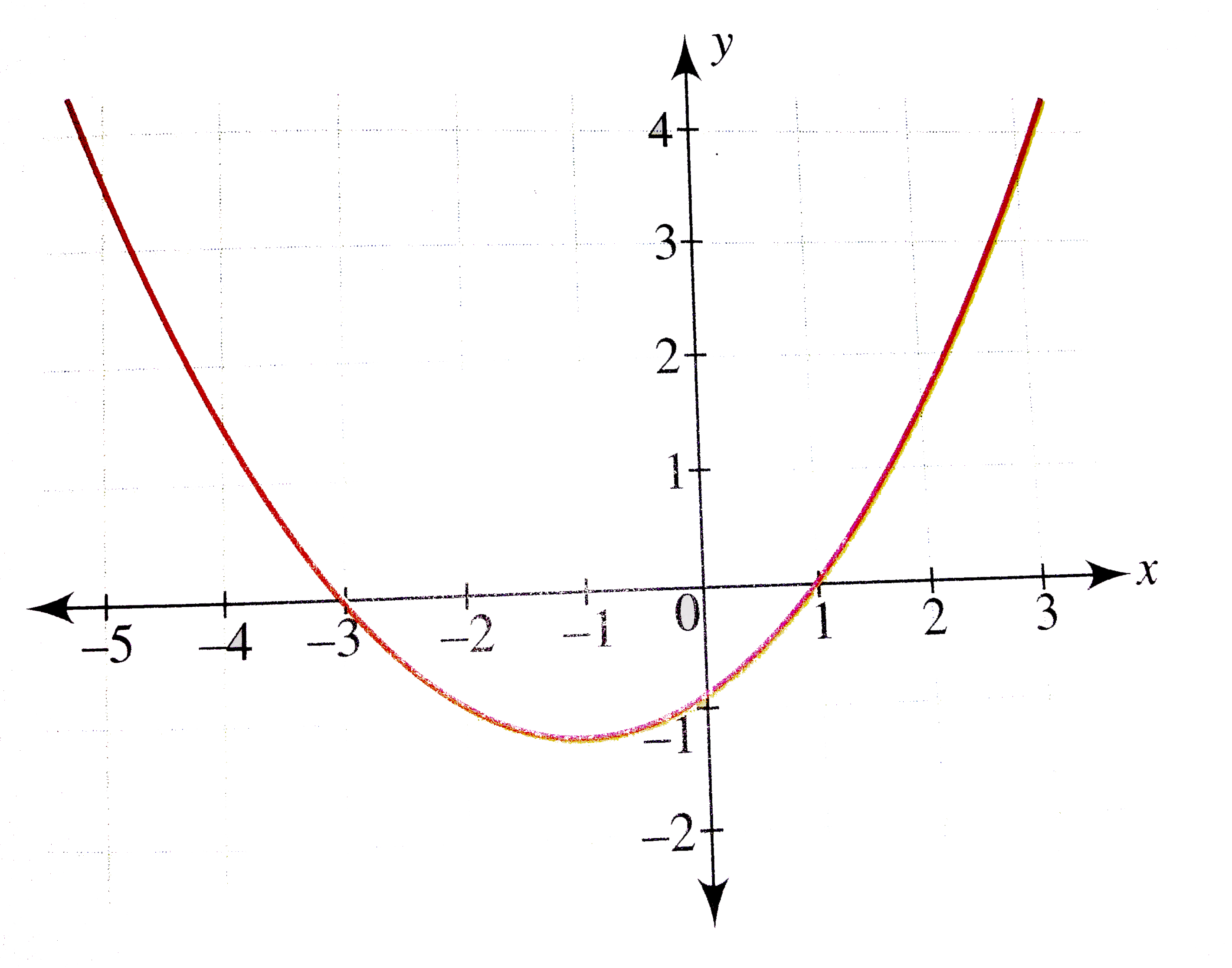 02:30View Solution
02:30View Solutionabout to only mathematics
05:31View SolutionDraw the graph and discuss the continuity of `f(x)=[sinx+cosx],x in [0,2pi],` where [.] represents the greatest integer function.
06:02View SolutionLet `f:R→R:f(x)=(x+1)` and `g:R→R:g(x)=(x^2 −4)`. Write down the formulae for `(fog)`.
01:44View Solution
Illustrations questions and complete solutions for chapter GRAPHICAL TRANSFORMATIONS of CENGAGE of Class 12
