Complete Solutions to QUESTION BANK of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| HIMALAYA PUBLICATION | QUESTION BANK |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Objective function of L.P.P is
01:19View SolutionWhich of the following set is not a convex set
View SolutionWhich of the following set is convex
View SolutionIf `X_(1) = (x_(1), y_(1))` and `X_(2) = (x_(2),y_(2))` are two optimal solutions of a L.P.P., then
04:55View SolutionThe optimal value of the objective function is attained at the points
View SolutionThe solution of inequality `x ge 0` is
View SolutionSolution set of the inequality `y le 0` is
View SolutionThe solution set of the inequalities `x ge 0` and `y le 0` is
View SolutionThe region represents by the inequalities `x ge 6, y ge 3, 2x + y ge 10, x ge 0, y ge 0` is
05:51View SolutionIf an LPP admits optimal solution at two consecutive vertices of a feasible region, then
00:45View SolutionThe feasible region of an L.P.P is always
01:09View SolutionThe minimum value of the linear objective function x = 5x + 2y subjected to `10x + 2y ge 20, 5x + 5y ge 30, x ge 0 , y ge 0` is
05:21View SolutionThe shaded region in the following figure is the solution set of the inequations,
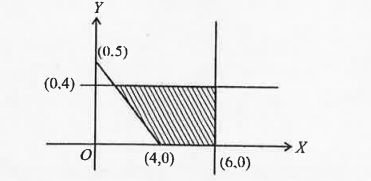 04:56View Solution
04:56View SolutionThe shaded region in the following figure is the solution set of the inequations,
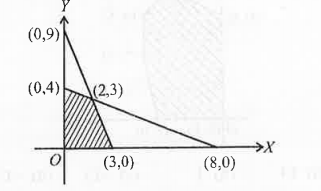 07:25View Solution
07:25View SolutionThe maximum value of linear objective function z = 40x + 50y subjected to `3x + y le 9, x + 2y lt 8, x ge 0, y ge 0` is
06:03View SolutionThe shaded region in the following figure is the solution set of the inequations,
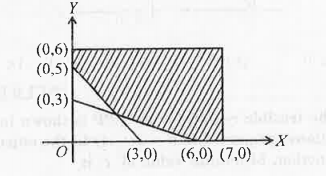 05:58View Solution
05:58View SolutionMaximum value of set z = 3x +2y subjected to `0 le x le 3, 0 le y le 3, x+y le 5, 2x + y ge 4`, is
11:20View SolutionThe shaded region in the following figure is the solution set of the inequations,
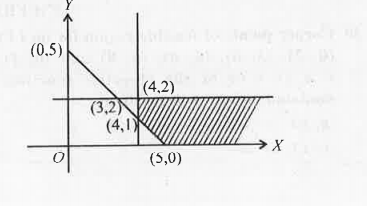 04:33View Solution
04:33View SolutionThe minimum value of z = 6x + 4y subjected to `2x + 3y le 30, 3x + 2y le 24, x + 4y le 3, x,y le 0`
04:27View SolutionThe region represented by the inequations `2x + 3y le 18, x + y ge 10, x ge 0, y ge 0` is
02:50View SolutionOptimization of the objective function is a process of
00:59View SolutionThe corner points of the feasible region determined by the system linear constraints are (0,10), (5,5), (15,15), (0,20). Let Z = px+ qy, where p, `q gt 0`, condition on p and q so that the maximum of Z occurs at both the points (15,15) and (0,20) is
02:37View SolutionFeasible region (shaded ) for a LPP is shown in the following figure
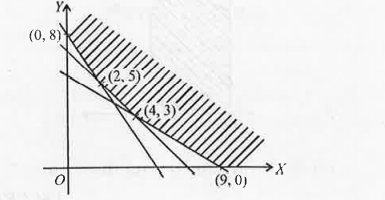 View Solution
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0,0), (0,40), (20,40), (60, 20), (60, 0). The objective function is Z = 4x + 3y. Compare the quantity in column in A and column B. Column A= Maximum of Z Column B= 325
03:19View SolutionThe feasible solution for a LPP is shown in the following figure. Let Z=3 x-4 y be the objective function. Minimum of Z occurs at
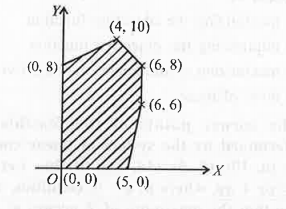 04:30View Solution
04:30View SolutionThe feasible solution for a LPP is shown in the following figure. Let Z=3 x-4 y be the objective function. Minimum of Z occurs at
 04:30View Solution
04:30View SolutionThe feasible solution for a LPP is shown in the following figure. Let Z=3 x-4 y be the objective function. (Maximum value of Z+ Minimum value of Z ) is
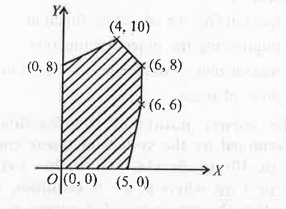 05:13View Solution
05:13View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3 x-4 y be the objective function. Maximum value of F is
 03:52View Solution
03:52View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3 x-4 y be the objective function. Minimum value of F is
 02:58View Solution
02:58View SolutionCorner points of feasible region for an LPP are (0,2),(3,0),(6,0),(6,8) and (0,5). Let F=4 x+6 y be the objective function. The minimum value of F occur at
03:14View SolutionIn the equation 33 Maximum of F - Minimum of F =
View SolutionCorner points of the feasible region determined by the system of linear constraints are `(0, 3), (1, 1) and (3, 0)`. Let `z=px+qy`, where `p, q gt 0`. Condition on p and q so that the minimum of z occurs at (3, 0) and (1, 1) is
03:04View Solution
QUESTION BANK questions and complete solutions for chapter LINEAR PROGRAMMING of HIMALAYA MATHS (KANNADA ENGLISH) of Class 12
