Complete Solutions to QUESTION BANK of chapter COMMON ENTRANCE TEST - 2014 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMMON ENTRANCE TEST - 2014 |
| HIMALAYA PUBLICATION | QUESTION BANK |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
Which one of the following is not correct for the features of exponential function given by `f(x) = b^(x)` where `b gt 1` ?
06:40View SolutionIf `y=(1+x)(1+x^(2))(1+x^(4))`, then `(dy)/(dx)` at `x=1` is
03:36View SolutionIf `y=(tan^(-1)x)^(2)` show that `(x^(2)+1)^(2)y_(2)+2x(x^(2)+1)y_(1)=2`
07:24View SolutionIf `f(x)=x^(3)` and `g(x)=x^(3)-4x` in `-2 le x le 2`, then consider the statements :
(i) `f(x)` and `g(x)` satisfy Rolle's theorem.
(ii) `f(x)` and `g(x)` both satisfy Rolle's theorem.
(iii) Only `g(x)` satisfies Rolle's theorem. Of these statements03:40View SolutionWhich of the following is not a correct statement?
00:43View SolutionIf the function f(x) satisfies `lim_(x rarr 1) (f(x) - 2)/(x^(2) - 1) = pi`, then `lim_(x rarr 1) f(x) =`
02:39View SolutionThe tangent to the curve `y=x^(3)+1` at(1, 2) makes an angle `theta` with y-axis, then the value of tan `theta` is
01:42View SolutionIf the function f(x) defined as `f(x) = (x^(100))/(100) + (x^(99))/(99) +….+(x^(2))/(2) + x + 1`, then `f'(0) =`
02:00View SolutionIf `f(x) = f(pi + e - x) and int_e^(pi) f(x) dx = 2/(e + pi)`, then `int_e^(pi) xf(x) dx` is equal to
03:24View SolutionIf linear function `f(x)` and `g(x)` satisfy `int[(3x-1)cosx+(1-2x)sinx]dx=f(x)cos x + g(x) sin x+C`, then
04:08View SolutionThe value of the integral `int_(-pi//4)^(pi//4) log (sec theta - tan theta)d theta` is
05:37View Solution`int(sin 2x)/(sin^(2)x + 2 cos^(2)x) dx =`
02:32View SolutionLet S be the set of all real numbers. A relation R has been defined on S by a Rb`rArr|a-b| le 1`, then R is
02:47View SolutionFor any two real numbers, an operation * defined by a *b = 1 + ab is
07:30View SolutionLet `f:NtoN`defined by :
`f(n)={:{((n+1)/(2) "if n is odd"),((n)/(2) "if n is even"):}`01:16View SolutionSuppose `f(x)=(x+1)^(2)` for `xge-1`. If g(x) is the function whose graph is the reflection of the graph of f(x) in the line y = x, then g(x) =
01:14View SolutionThe domain of the function `f(x)=sqrt(cos x)` is
02:41View SolutionIn a class of 60 students, 25 students play cricket and 20 students play tennis and 10 students play both the games, then the number of students who play neither is
02:10View SolutionGiven `0 le x le (1)/(2)` then the value of `tan[sin^(-1){(x)/(sqrt(2)) + sqrt(1-x^(2))/(sqrt(2))}-sin^(-1)x]` is
05:23View SolutionThe value of `sin(2 sin^(-1) 0.8)` is equal to
02:09View SolutionIf A is `3 xx 4` matrix and B is a matrix such that `A^(1)B` and `B A^(1)` are both defined, then B is of the type
02:45View SolutionThe symmetric part of the matrix `A = ((1,2,4),(6,8,2),(2,-2,7))` is
05:24View SolutionIf A is a matrix of order 3, such that A(adj A) = 101, then |adj A| =
01:57View SolutionConsider the following statements :
(a) If any two rows or columns of a determinant are identical, then the value of the determinant is zero
(b) If the corresponding rows and columns of a determinant are interchanged, then the value of the determinant does not change.
(c) If any two rows or columns of a determinant are interchanged, then the value of the determinant changes in sign.
Which of these are correct ?04:13View SolutionThe inverse of the matrix `A=[(2,0,0),(0,3,0),(0,0,4)]` is
01:26View SolutionIf a, b and c are in A.P., then the value of `|(x+2, x+3, x+a),(x+4, x+5, x+b),(x+6, x+7, x+c)|` is
03:02View SolutionThe local minimum value of the function f' given by `f(x) = 3 + |x|, x in R` is
02:00View SolutionA stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/sec. At that instant, when the radius of circular wave is 8 cm, how fast is the enclosed area is increasing
04:22View SolutionA gardener is digging a plot of land. As he gets tired, he works more slowly. After 't' minutes he is digging at a rate of `(2)/(sqrt(t))` square metres per minutes. How long will it take him to dig an area of 40 square meters ?
03:31View SolutionThe area of the region bounded by the lines `y=mx, x =1, x=2`, and `x` axis is 6sq. units then 'm' is
01:49View SolutionArea of the region bounded by two parabolas `y = x^(2)` and `x = y^(2)` is
06:51View SolutionThe order and degree of the differential equation `y = x(dy)/(dx) + (2)/((dy)/(dx))` is
04:16View SolutionThe general solution of the differential equation `(dy)/(dx)+y/x=3x` is
02:16View SolutionThe distance of the point P(a, b, c) from the x-axis is
01:23View SolutionEquation of the plane perpendicular to the line `x/1=y/2=z/3` and passing through the point (2, 3, 4) is
02:17View SolutionThe line `(x-2)/(3) = (y-3)/(4) = (z-4)/(5)` is parallel to the plane
06:07View SolutionThe angle between two diagonals of a cube is
06:19View SolutionThe lines : `(x-2)/1=(y-3)/1=(z-4)/(-k)` and `(x-1)/k =(y-4)/2 =(z-5)/1` are co-planar if :
01:55View SolutionA and B are two events such that `P(A)!=0, P(B//A)` is
01:51View SolutionTwo dice are thrown simultaneously. The probability of obtaining a total score of 5 is
05:03View SolutionIf the events A and B are independent if `P(A')=2/3` and `P(B')=2/7`, then `P(A nn B)` is equal to
01:41View SolutionA box contains 100 bulbs, out of which 10 are defective. A sample of 5 bulbs is drawn. The probability that none is defective is
05:41View SolutionThe area of the parallelogram whose adjacent sides are `hati + hatk and 2 hati + hatj + hatk` is :
01:40View SolutionIf `vec(a)` and `vec(b)` are two unit vectors inclined at an angle `pi/3`, then the value of `|vec(a)+vec(b)|` is
01:57View SolutionThe value of `[vec(a)-vec(b) vec(b)-vec(c) vec(c)-vec(a)]` is equal to
00:31View SolutionIf `x+y le 2, x ge 0, y le 0` the point at which maximum value of `3x+2y` attained will be
03:03View SolutionIf `sin theta= sin alpha`, then
02:05View SolutionIf `tanx=3/4, pi lt x lt (3 pi)/(2)`, then the value of `cos. x/2` is
02:53View SolutionIn a triangle ABC, `a[b cos C - c cos B]=`
02:14View SolutionIf `alpha` and `beta` two different complex numbers with `|beta|=1`, then `|(beta-alpha)/(1-bar(alpha)beta)|` is equal to
03:41View SolutionThe set `A={x:|2x+3| lt 7}` is equal to the set
01:21View SolutionHow many 5 digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once ?
01:32View SolutionIf `21^(st)` and `22^(nd)` terms in the expansion of `(1+x)^(44)` are equal, then `x` is equal to
03:32View SolutionConsider an infinite geometric series with first term 'a' and common ratio 'r'. If the sum is 4 and the second term is `3/4` then
03:49View SolutionA straight line passes through the points (5, 0) and (0, 3). The length of perpendicular from the point (4, 4) on the line is
04:53View SolutionEquation of circle with centre (-a, -b) and radius `sqrt(a^(2) - b^(2))` is
02:37View SolutionThe area of the triangle formed by the lines joining the vertex of the parabola `x^(2)=12y` to the ends of latus rectum is
03:10View SolutionIf the coefficient of variation and standard deviation are 60 and 21 respectively, the arithmetic mean of distribution is
01:41View SolutionThe fucntion represented by the following graph is
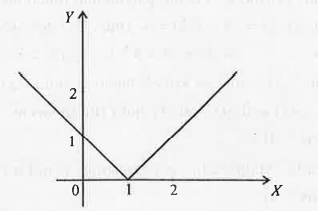 01:42View Solution
01:42View SolutionIf `f(x) = {{:((3 sin pi x)/(5 x),x ne 0),(2k,x = 0):}` is continuous at x = 0, then the value of k is equal to :
01:36View Solution
QUESTION BANK questions and complete solutions for chapter COMMON ENTRANCE TEST - 2014 of HIMALAYA MATHS (KANNADA ENGLISH) of Class 12
