Complete Solutions to QUESTION BANK of chapter COMMON ENTRANCE TEST - 2017 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMMON ENTRANCE TEST - 2017 |
| HIMALAYA PUBLICATION | QUESTION BANK |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
If A and B are finite sets and `A subset B`, then
02:04View SolutionThe value of `cos ^(2)45^(@) - sin^(2)15^(@)` is
01:46View Solution3 + 5 + 7 + .... to n terms is
01:05View SolutionIf `((1+i)/(1-i))^(m)=1`, then the least positive integral value of m is
02:03View SolutionIf `|x-2|le 1`, then
01:44View SolutionIf `'^(n)C_(12) = ""^(n)C_(8)` then n is equal to
00:50View SolutionThe total number of terms in the expansion of `(x+a)^(47)-(x-a)^(47)` after simplification is
07:55View SolutionEquation of line passing through the point (1,2) and perpendicular to the line y = 3x - 1 is
02:11View SolutionThe eccentricity of the ellipse `(x^(2))/(36)+ (y^(2))/(16)=1` is
02:20View SolutionThe perpendicular distance of the point P(6,7,8) from XY-plane is
01:57View SolutionThe value of `lim_(theta to 0)(1-cos 4theta)/(1-cos 6 theta)` is
05:09View SolutionWrite the converse and contrapositive of the statement " If x is a prime number then x is odd "
01:56View SolutionIf coefficient of variation is 60 and standard deviation is 24, then arithmetic mean is
01:09View SolutionThe range of the function `f(x) = sqrt(9-x^(2))`
03:11View SolutionLet `f: R to R` be defined by `f(x) = x^(4)`, then
01:47View SolutionThe range of `sec^(-1)x` is
01:23View SolutionIf `tan^(-1)x + tan^(-1)y=4pi//5`, then `cot^(-1)x + cot^(-1)y` is equal to
04:37View SolutionIf `f(x) = 8x^(3), g(x) = x^((1//3))`, then fog(x) is
00:56View SolutionIf `A = 1/pi [(sin^(-1)(xpi),tan^(-1)(x/pi)),(sin^(-1)(x/pi),cot^(-1)(pix))]`
`B = 1/pi [(-cos^(-1)(xpi),tan^(-1)(x/pi)),(sin^(-1)(x/pi),-tan^(-1)(pix))] `
then `A-B ` is equal to :02:12View SolutionIf a matrix A is both symmetric and skew symmetric, then
00:47View SolutionIf `2[[1,3],[0,x]]+ [[y,0],[1,2]]= [[5,6],[1,8]]` , then the value of x and y are
02:21View SolutionBinary operation * on R `-{-1}` defined by `a ** b = (a)/(b+1)` is
05:29View Solution`|[3,x],[x,1]|= |[3,2],[4,1]|` then x is equal to
00:42View SolutionIf A is a square matrix of order `3 xx 3`, then |KA| is equal to
00:56View SolutionThe area of triangle with vertices (K, 0), (4,0), (0, 2) is 4 square units, then value of K is
03:23View SolutionLet `Delta=|(Ax,x^(2),1),(By,y^(2),1),(Cz,z^(2),1)|` and `Delta_(1)=|(A,B,C),(x,y,z),(zy,zx,xy)|` then
05:31View SolutionIf `F(x)= {(Kx^(2) if x le 2),(3 if x gt 2):}` is continuous at x = 2, then the value of K is
01:07View SolutionThe value of C in mean value theorem for the function `f(x)=x^(2)` in [2, 4] is
05:24View SolutionThe point on the curve `y^(2) = x` where the tangent makes an angle `(pi)/(4)` with X-axis is
02:03View SolutionThe function `f(x)=x^(2)+2x-5` is strictly increasing in the interval
03:16View SolutionThe rate of change of volume of a sphere with respect to its surface area when the radius is 4 cm is
05:24View SolutionIf `y=tan^(-1)((sin x + cos x)/(cos x - sin x))`, then `(dy)/(dx)` is equal to
04:29View SolutionIf `y=|(f(x),g(x),h(x)),(1,m,n),(a,b,c)|`, then `(dy)/(dx)` is equal to
05:37View SolutionIf `sin x = (2t)/(1+t^(2)), tan y = (2t)/(1-t^(2))`, then `(dy)/(dx)` is equal to
02:47View SolutionThe derivative of `cos^(-1)(2x^(2)-1)` w.r.t `cos^(-1)` x is
06:09View SolutionIf y = log (log x) then `(d^(2)y)/(dx^(2))` is equal to
05:30View Solution`int ((x+3)e^(x))/((x+4)^(2)) dx` is equal to
01:31View Solution`int (cos2x - cos 2theta)/(cosx- costheta)dx` is equal to
02:54View Solution`int sqrt(x^(2)+ 2x+5) dx` is equal to
02:29View Solution`int_(0)^(pi//2)(tan^(7)x)/(cot^(7)x + tan^(7)x)dx` is equal to
05:54View Solution`int_(-5)^(5)|x+2|dx` is equal to
02:42View Solution`int_-(pi//2)^(pi//2) (dx)/(e^(sinx)+1)` is equal to
02:30View Solution`int_(0)^(pi//2)(1)/(a^(2).sin^(2)x+b^(2).cos^(2)x)dx` is equal to
07:31View SolutionThe area of the region bounded by the curve `y = x^(2)` and the line y = 16 is
03:02View SolutionArea of the region bounded by the curve y = cos x, x = 0 and `x = pi` is
06:04View SolutionThe degree of the differential equation `[1+((dy)/(dx))^(2)]^(2)=(d^(2)y)/(dx^(2))`
02:58View SolutionGeneral solution of differential equation `(dy)/(dx)+y=1(y ne 1)` is
01:49View SolutionThe integrating factor of the differential equation `x.(dy)/(dx)+2y=x^(2)` is `(x ne 0)`
02:29View Solutionif `vec a= 2 hat i+ lambda hat j+ hat k` and `vec b= hat i+ 2 hat j+ 3 hat k` are orthogonal then the value of `lambda`
01:23View SolutionIf `vec a, vec b, vec c` are unit vectors such that `vec a + vec b + vec c = vec 0`, then the value of `vec a . vec b + vec b.vec c + vec c vec a` is equal to
04:29View SolutionIf `vec a` and `vec b` are unit vectors, then angle between `vec a` and `vec b` for `sqrt(3)vec a - vec b` to be unit vector is
01:33View SolutionReflection of the point `(alpha, beta, gamma)` in XY plane is
01:23View SolutionThe plane `2x-3y+6z-11=0` makes an angle `sin^(-1)(alpha)` with X - axis. The value of `alpha` is equal to
05:00View SolutionThe distance of the point (-2, 4, -5) from the line `(x +3)/(3)= (y - 4)/(5)= (z +8)/(6)` is
05:19View SolutionA box has 100 pens of which 10 are defective. The probability that out of a sample of 5 pens drawn one by one with replacement and atmost one is defective is
05:35View SolutionTwo events A and B will be independent if
03:11View SolutionThe probability distribution of X is The value of k is
 01:30View Solution
01:30View SolutionThe shaded region in the figure is the solution set of the inequations
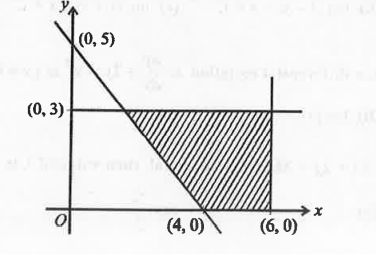 07:37View Solution
07:37View SolutionIf an LPP admits optimal solution at two consecutive vertices of a feasible region, then
00:45View Solution`int_(0.2)^(3.5)[x]dx` is equal to
05:38View Solution
QUESTION BANK questions and complete solutions for chapter COMMON ENTRANCE TEST - 2017 of HIMALAYA MATHS (KANNADA ENGLISH) of Class 12
