Complete Solutions to QUESTION BANK of chapter COMMON ENTRANCE TEST - 2018 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMMON ENTRANCE TEST - 2018 |
| HIMALAYA PUBLICATION | QUESTION BANK |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
The integrating factor of `(dy)/(dx)+y=(1+y)/x` is
02:54View SolutionIf `|vec a xx vec b|^(2)` + `|vec a . vec b|^(2)` = 144` and |a| = 4, then the value of |b| is
02:44View SolutionIf `vec a` and `vec b` are mutually perpendicular unit vectors, then (3`vec a` + 2`vec b`). (5`vec a` - 6 `vec b`)= `
03:04View SolutionIf the vectors `ahati+hatj+hatk,hati+bhatj+hatk and hati+hatj+chatk` are coplanar `(a ne b ne c ne 1)` , then the value of `abc - (a+b+c) =`
02:12View SolutionIf `vec a = i + lambda j + 2k, vec b = mui + j - k` are orthogonal and` |vec a| = |vec b|` then `(lambda, mu) =`
05:05View SolutionThe image of the point (1,6,3) in the line `x/1=(y-1)/2=(z-2)/3` is
05:15View SolutionThe angle between the lines `2x = 3y = - z` and `6x =-y = 04z` is
03:35View SolutionThe value of k such that the line `(x-4)/1=(y-2)/1=(z-k)/2` lies on the plane 2x - 4y + z = 7 is
01:48View SolutionThe locus represented by `xy+yz=0` is
01:03View SolutionThe feasible region of an Lpp is shown in the figure. If z= 3x+9y, then the minimum variable occurs at
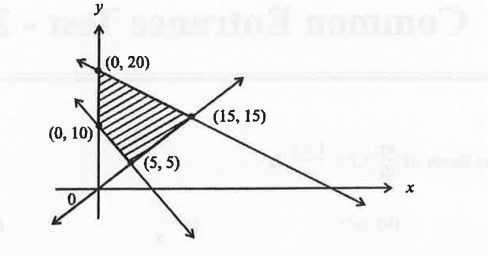 01:36View Solution
01:36View SolutionFor the LPP, maximize z = x + 4y subject to the constraints `x + 2y le 2, x +2y ge 8, x, y ge 0`.
03:14View SolutionFor the probability distribution given by the standard deviation `(sigma)` is
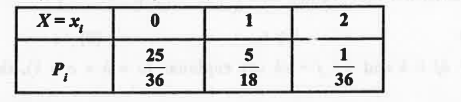 04:14View Solution
04:14View SolutionA bag contains 17 tickets numbered from 1 to 17. A ticket is drawn at random, the another ticket is drawn without replacing the first one. The probability that both the tickets may show even number is
03:53View SolutionA flashlight has 10 batteries out of which 4 are dead . If 3 batteries are selected without replacement and tested , then the probability that all 3 are dead is
02:04View SolutionIf `|x+5| ge 10`, then
01:41View SolutionEverybody in a room shakes hands with everybody else. The total number of handshakes is 45. The total number of persons in the room is
01:17View SolutionThe constant term in the expansion of `(x^(2)-1/x^(2))^(16)` is
05:49View SolutionIf P(n):` "''" 2^(2n)-1` is divisible by k for all `n in N"''" ` is true, then the value of 'K' is
04:00View SolutionThe equation of the line parallel to the line `3x-4y+2=0` and passing through (-2,3) is
06:51View SolutionIf `((1-i)/(1+i))^(96)=a+ib`, then (a,b) is
04:03View SolutionThe distance between the foci of a hyperbola is 16 and its eccentricity is `sqrt2` . Its equation is :
01:54View SolutionThe number of the ways in which 5 girls and 3 boys can be seated in a row so that no two boys are together is
03:01View SolutionIf a,b,c are three consevutive terms of an AP and x,y,z are three consecutive terms of a GP, then the value of `X^(b-c).Y^(c-a). Z^(a-b)` is
07:22View SolutionThe value of `{:(lim),(xrarr0):}(|x|)/x` is
01:11View SolutionLet `f(x) = x - 1/x` , then f' (-1) is
00:54View SolutionThe negation of the statement ' 72 is divisible by 2 and 3' is
02:32View SolutionThe probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then the probability of neither A nor B is
02:48View SolutionIn a simultaneous throw of a pair of dice, the probability of getting a total more than 7 is
03:28View SolutionIf A and B are mutually exclusive events, given that `P(A)=3/5,P(B)=1/5`, then P(A or B) is
01:39View SolutionLet f, g : `R rarrR` be two functions defined as `f(x) = |x| + x and g(x) = | x| - x AA x in R.` . Then (fog ) (x) for `x lt 0` is
02:42View SolutionA is a set having 6 distinct elements. The number of distinct functions from A to A which are not bijections is
05:09View SolutionLet `f : R rarrR` be defined by
`f(x)={{:(2x ,,,x gt3 ),(x^2,,,1 lt xle3),(3x,,,x le1):}`
Then f(-1) + f(2) + f(4) is02:40View SolutionIf `sin^(-1) x + cos ^(-1) y = (2pi)/5 ` , then `cos^(-1) x + sin ^(-1) y ` is
01:37View SolutionThe value of the expression `tan(1/2cos^(-1)""2/sqrt5)` is
02:11View Solutionif `A =[(2,-2),(-2,2)]," then " A^(n)=2^(k)A`, where k=
07:19View SolutionIf `[(1,1),(-1,1)][(x),(y)]=[(2),(4)],` then the values of x and y respectively are
01:13View SolutionIf `A=[(cos alpha, sin alpha),(-sin alpha, cos alpha)]`, then verify that `A'A=I`
04:00View SolutionIf `x,y,z in R`, then the value of determinant
`|((5^(x)+5^(-x))^(2) , (5^(x)-5^(-x))^(2),1),((6^(x)+6^(-x))^(2),(6^(x)-6^(-x))^(2), 1),((7^(x)+7^(-x))^(2),(7^(x)-7^(-x))^(2),1)|` is04:45View SolutionThe value of determinant
`|(a-b ,b+c,a),(b-a,c+a,b),(c-a,a+b,c)|` is05:37View SolutionIf `(x_(1),y_(1)),(x_(2),y_(2)) and (x_(3),y_(3))` are the vertices of a triangle whose area is 'k' square units, then `|(x_(1),y_(1),4),(x_(2),y_(2),4),(x_(3),y_(3),4)|^(2)` is
04:26View SolutionLet A be a square matrix of order `3xx3` , then |5A| =
01:18View SolutionIf `f(x)={{:(sqrt(1+kx)-sqrt(1-kx)," if ", -1le x lt 0),((2x+1)/(x-1), " if ", x le x le1):}`
is continuous at x = 0 , then the value the of k is02:16View SolutionIf cosy = xcos (a+y) with `cos a ne pm1` , then `(dy)/(dx)` is equal to
03:50View SolutionIf `f(x) = |cosx-sinx|,` then `f ' (pi//6)` is equal to
01:48View SolutionIf `y=sqrt(x+sqrt(x+sqrt(x+............oo)))`, m then `dy/dx=`
04:42View SolutionIf `f(x)={{:((log_ex)/(x-1),,,x ne 1),(k,,,x=1):}`is continuous at x = 1 , then the value of k is
01:20View SolutionApproximate change in the volume V of a cube of side x metres caused by increasing the side be 3% is
01:23View SolutionThe maximum value of `(1/x)^(x)` is
06:38View Solution`f(x)=x^(x)` has a stationary point at :
00:37View SolutionThe maximum area of a rectangle inscribed in the circle `(x+1)^(2)+(y-3)^(2)=64` is
02:35View Solution`int1/(1+e^(x))dx` is equal to
02:15View Solution`int1/(sqrt(3-6x-9x^(2)))dx` is equal to
02:34View Solution`int" e"^(sinx).((sinx+1)/(secx))dx` is equal to
02:11View Solution`int_(-2)^2 |x cos pi x|dx` is equal to :
04:03View Solution`int_(0)^(1)(dx)/(e^(x)+e^(-x))` is equal to
02:14View Solution`int_0^(1//2)(dx)/((1+x^2)sqrt(1-x^2))` is equal to
04:34View SolutionArea of the region bounded by the curve y = cos x, x = 0 and `x = pi` is
06:04View SolutionThe area bounded by the line y = x,x axis and ordinates x = -1 and x = 2 is
03:04View SolutionThe degree and the order of the differential equation `(d^(2)y)/(dx^(2))=root3(1+((dy)/(dx))^(2)` respectively are
04:35View SolutionThe solution of the differential equation `x(dy)/(dx)-y=3` represents a family of
02:06View Solution
QUESTION BANK questions and complete solutions for chapter COMMON ENTRANCE TEST - 2018 of HIMALAYA MATHS (KANNADA ENGLISH) of Class 12
