Complete Solutions to पेपर 1 of chapter साल्वड पेपर 2017 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | साल्वड पेपर 2017 |
| JEE Main & Advanced (Hindi Medium) | पेपर 1 |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
माना कि X और Y इस प्रकार की दो घटनाएँ (events) हैं कि `P(X) =1/3,P(X/Y) = 1/2` और `P(Y/X) =2/5` है। तब
05:06View Solutionमाना की ` f: R to (0,1) ` एक सतत फलन ( continuous functions ) है|तब निम्न फलनों में से कौन से फलन( नों) का ( के ) मान अंतराल ( interval ) (0 ,1 ) के किसी बिंदु पर शून्य होगा?
07:03View Solutionमाना कि a, b, x और y इस प्रकार की वास्तविक सँख्यायें (real numbers) हैं कि a-b = 1 और `y ne 0` हैं। यदि सम्मिश्र सँख्या (complex number) z = x + iy , Im `((az+b)/(z +1)) = y` को संतुष्ट करती है, तब निम्न में से कौन सा(से) x का(के) सम्भावित मान है(हैं)?
(i) ` - 1 + sqrt(1 - y^2)` (ii) `1 - sqrt(1 +y^2)` (iii) `1+ sqrt(1+y^2)` (iv) `-1-sqrt(1-y^2)`03:56View Solutionयदि `2x-y+1=0` अतिपरवलय `(x^(2))/(a^(2))-(y^(2))/(16)=1` की स्पर्शरेखा है तो निम्न में से कौनसी समकोणीय त्रिभुज की भुजायें नहीं हो सकती है (हैं)
04:00View Solutionमाना कि x से छोटा या x के समान सबसे बड़ा पूर्णांक [x] है। तब फलन `f(x)=xcos (pi(x+[x]))` निम्न में से किन बिंदुओं पर असतत है
03:39View Solutionनिम्न में से कौन-सा/से वास्तविक संख्याओं के `3 xx 3` आव्यूह (matrix) का वर्ग। (square) नहीं है/है?
01:55View Solutionयदि परवलय (parabola) `y^2 = 16x` की एक जीवा (chord), जो स्पर्शरेखा (tangent) नहीं है, का समीकरण 2x +y = p तथा मध्यबिन्दु (midpoint) (h,k) है, तो निम्न में से p, hएवं k के सम्भावित मान है(है)?
06:35View Solutionवास्तविक संख्या `alpha` के लिए यदि रैखिक समीकरण निकाय `[(1,alpha,alpha^(2)),(alpha,1,alpha),(alpha^(2),alpha,1)][(x),(y),(z)]=[(1),(-1),(1)]` के अनन्त हल है तब `1+alpha+alpha^(2)=`
03:56View Solutionएक समकोणीय त्रिभुज की भुजाये समान्तर श्रेणी में है यदि इसका क्षेत्रफल 24 है तब इसकी सबसे छोटी भुजा की लम्बाई क्या है
03:03View Solutionमाना की `f: R to R` इस प्रकार का अवकलनीय फलन (differentiable function) है की `f(0), 0, f(pi/2)=3" एव "f'(0)=1" है|"`
यदि `x in (0, pi/2]" के लिए "g(x)=int_(x)^(x/2) [f'(t)" cosec t-cot t cosec f(t) dt ]" है तब "underset(x to 0)lim g(x)=`04:40View Solutionp के कितने मनो के लिए वृत्त (circle) `x^(2)+y^(2)+2x+4y-p=0` एव निर्देशांक अक्षो (coordinate axes) में केवल तीन बिंदु उभयनिष्ट (common) है
06:07View SolutionA,B,C,D,E,F,G,H,I,J से 10 लम्बाई के शब्द बनाये जाये है माना की x इस तरह के ऊब शब्दों की संख्या है जिनमे किसी भी अक्षर की पुनःवृति नहीं होती है तथा y इस तरह के उन शब्दों की संख्या है जिनमे केवल एक अक्षर की पुनःवृति दो बार होती है व् किसी अन्य अक्षर की पुनःवृति नहीं होती है तब `y/(9x)=`
02:02View Solution
`a=sqrt2` के लिए उपयुक्त कनिक (कलाम I) पर स्पर्शरेखा खींची जाती है जिसका स्पर्शबिन्दु (-1,1) है| तब निम्न में से कौन सा विकल्प द्वारा स्पर्शरेखा का समीकरण प्राप्त करने का केवल सही सयोजन है07:50View Solutionनिचे दी गयी टेबल के तीन कॉलमों में उपलब्ध सूचना का उपयुक्त ढंग से सुमेल कर प्रश्नों के उत्तर दीजिये |

`a=sqrt(2)` के लिए उपयुक्त शांकव (कॉलम 1) के स्पर्शबिन्दु `(-1,1)` पर एक स्पर्शरेखा खींची जाती है तब निम्न में से केवल कौन सा विकल्प इस स्पर्शरेखा का समीकरण प्राप्त करने का सही संयोजन है03:53View Solutionयदि उपयुक्त शांकव (कलाम I) के बिंदु स्पर्शरेखा (8,16) पर स्पर्शरेखा y=x+8 है तब निम्न में से कौन-सा विकल्प सही सयोजन है
04:00View Solution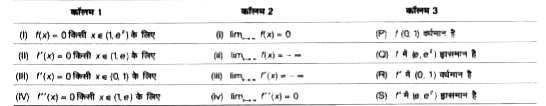
निम्न में से कौन-सा विकल्प केवल गलत सयोजन (only Incorrect combination) है17:09View Solution
निम्न में से कौन-सा विकल्प केवल सही है17:09View Solution
निम्न में से कौन-सा विकल्प केवल सही है17:09View Solution
पेपर 1 questions and complete solutions for chapter साल्वड पेपर 2017 of JEE MAINS & ADVANCED MATHS (HINDI) of Class 12