Complete Solutions to पेपर 2 (खण्ड 3) of chapter JEE ADVANCED सोल्वड पेपर्स 2018 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE ADVANCED सोल्वड पेपर्स 2018 |
| JEE Main & Advanced (Hindi Medium) | पेपर 2 (खण्ड 3) |
| Number Of Questions | 4 |
| Academic Year | 2023-24 |
माना की `E_(1) = {x in R: x ne 1 "और" x/(x-1) gt 0}` और `E_(2) ={x in E_(1)sin^(-1)(log_(e)(x/(x-1))}` एक वास्तविक संख्या (real number) है|
(यहाँ प्रतिलोम त्रिकोणमितीय फलां (inverse trignometric function) `sin^(-1)x,[-pi/2, pi/2]` में मान धारण करता है|
माना की फलन: `f:E_(1) to R, f(x) =log_(e)(x/(x-1))` के द्वारा परिभाषित है
और फलन `f: E_(2) to R, g(x) = sin^(-1) llog_(e)(x/(x-1))` के द्वारा परिभाषित है|

दिए हुए विकल्पों में से सही विकल्प है10:52View Solutionएक हाई स्कूल (high school) में, 6 बालकों `M_1 ,M_2 ,M_3,M_4,M_5, M_6` और 5 बालिकाओं `G_1 ,G_2, G_3 ,G_4 ,G_5,` के समूह (group) में से एक समिति (committee) बनाई जानी है। (i) माना कि `alpha_1` समिति को इस प्रकार से बनाने के तरीकों (ways) की कुल संख्या है कि समिति में 5 सदस्य हैं, जिनमें से ठीक (exactly) 3 बालक और 2 बालिकाएँ हैं। (ii) माना कि `alpha_2` समिति को इस प्रकार से बनाने के तरीकों की कुल संख्या है कि समिति में कम से कम (atleast) 2 सदस्य हैं, और बालकों और बालिकाओं की संख्या बराबर (equal) है। (iii) माना कि `alpha_3` समिति को इस प्रकार से बनाने के तरीकों की कुल संख्या है कि समिति में 5 सदस्य हैं, जिनमें से कम से कम 2 बालिकाएँ हैं। (iv) माना कि `alpha_4` समिति को इस प्रकार से बनाने के तरीकों की कुल संख्या है कि समिति में 4 सदस्य हैं, जिनमें से कम से कम 2 बालिकाएँ हैं और `M_1` व `G_1` समिति में एक साथ नहीं हैं।

दिए हुए विकल्पों में से सही विकल्प है:13:28View Solutionमाना कि H : `x^2/a^2-y^2/b^2=1` , जहाँ `a>b>0,xy` समतल (plane) में एक ऐसा अतिपरवलय (hyperbola) है जिसका संयुग्मी अक्ष (conjugateaxis) LM उसके एक शीर्ष (vertex)N पर `60^@` का कोण (angle) अंतरित (subtend) करता है। माना कि त्रिभुज (triangle) LMN का क्षेत्रफल (area) `4sqrt3` है।
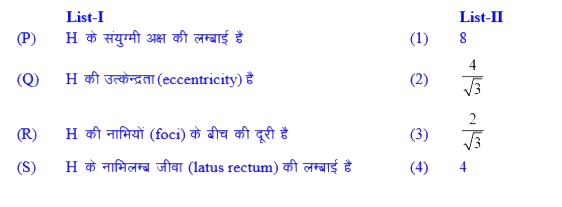
दिए हुए विकल्पों में से सही विकल्प है09:10View Solutionमाना कि फलन
`f_(1):RtoR,f_(2):(-(pi)/2,(pi)/2)to R,f_(3):(-1,e^((pi)/2)-2)toR` और `f_(4):RtoR` इस प्रकार परिभाषित है कि
(i) `f_(1)(x)=sin(sqrt(1-e^(-x^(2))))`,
(ii) `f_(2)(x)={((|sinx|)/(tan^(-1)x)"if",x!=0),(1,"if"x=0):}` जहां प्रतिलोम त्रिकोणमितीय फलन `tan^(-1)x,(-(pi)/2,(pi)/2)` में मान धारण करता है
(iii) `f_(3)(x)=[sin(log_(e)(x+2))]`, जहां `t epsilon R` के लिए [t],t से छोटा या t के बराबर महत्तम पूर्णांक को दर्शाता है।
(iv) `f_(4)(x)={(x^(2)sin(1/x),यदि x!=0),(x,यदिx=0):}`
 11:44View Solution
11:44View Solution
पेपर 2 (खण्ड 3) questions and complete solutions for chapter JEE ADVANCED सोल्वड पेपर्स 2018 of JEE MAINS & ADVANCED MATHS (HINDI) of Class 12