Complete Solutions to बहुविकल्पीय प्रश्न I of chapter सम्मिश्र संख्याएँ of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सम्मिश्र संख्याएँ |
| JEE Main & Advanced (Hindi Medium) | बहुविकल्पीय प्रश्न I |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
सबसे छोटा धन पूर्णांक `"(positive integer)"` '`n`' जिसके लिए `((1+i)/(1-i))^(n)=1` होगा, है
05:54View Solutionसम्मिश्र संख्या `z=x+iy`, जो समीकरण `|(z-5i)/(z+i)|=1` को सन्तुष्ट करेगी, स्थित होगी
03:26View Solutionयदि `z=((sqrt(3))/(2)+(i)/(2))^(5)+((sqrt(3))/(2)-(i)/(2))^(5)`, तब
04:25View Solutionनिम्नलिखित में कौन - सा क्षेत्र असमीका `|z-4|lt|z-2|` द्वारा प्रदर्शित होगा ?
03:37View Solutionयदि `z=x+iy` और `w=((1-iz))/((z-i))`, तब `|w|=1 सम्मिश्र तल में इंगित करता है कि
05:31View Solutionबिन्दु `z_(1), z_(2), z_(3), z_(4)` क्रम से लेने पर सम्मिश्र तल में एक समान्तर चतुर्भुज के शीर्ष होंगे, यदि और केवल यदि
02:24View Solutionयदि सम्मिश्र संख्याएँ a,b,c और u,v,w दो त्रिभुजों के शीर्षों को प्रदर्शित करती है, जो इस प्रकार है कि `c=(1-r)a+rb` और `w=(1-r)u+rv`, जहाँ r एक सम्मिश्र संख्या है, तब दोनों त्रिभुज
07:40View Solution`sum_(k=1)^(6) ("sin"(2pik)/(7)-i "cos"(2pik)/(7))` का मान है -
03:44View Solutionयदि `z_(1)` व `z_(2)` दो अशून्य (non - zero) सम्मिश्र संख्याएँ इस प्रकार है कि `|z_(1)+z_(2)|=|z_(1)|+|z_(2)|`, तब
कोणांक `(z_(1))-` कोणांक `(z_(2))` का मान होगा06:06View Solutionx के किस मान के लिए सम्मिश्र संख्याएँ `sin x + i cos 2x` और `cos x - i` एक - दूसरे की संयुग्मी (conjugate) होंगी ?
02:46View Solutionयदि `omega (ne 1)` इकाई का घनमूल है और `(1+omega)^(7)=A+B omega` हो, तो A और B क्रमशः होंगे
02:28View Solutionमाना z और w दो अशून्य सम्मिश्र संख्याएँ इस प्रकार है कि `|z|=|w|` और कोणांक (z) + कोणांक `(w)=pi`, तब z बराबर होगा |
05:54View Solutionमाना z व w दो सम्मिश्र संख्यायें इस प्रकार हैं कि |z|`le` 1, |w|`le` 1 तथा `|z-iw|=|z-ibarw|=2`, तब z का मान है
07:26View Solutionघन पूर्णांक `n_(1)` व `n_(2)` के लिए व्यंजक
`(1+i)^(n_(1))+(1+i^(3))^(n_(1))+(1-i^(5))^(n_(2))+(1+i^(7))^(n_(2))`, जहाँ `i=sqrt(-1)`, का मान वास्तविक होगा, यदि और केवल यदि08:41View Solutionयदि `omega` इकाई का एक काल्पनिक घनमूल है, तो `(1+omega-omega^(2))^(7)` का मान होगा
01:48View Solution`sum_(n=1)^(13)(i^(n)+i^(n+1))`, जहाँ `i=sqrt(-1)`, का मान होगा
03:33View Solutionयदि `|(6i,-3i,1),(4,3i,-1),(20,3,i)|=x+iy`, तब
03:31View Solutionयदि `I = sqrt(-1)`, तब `4+5(-(1)/(2)+(I sqrt(3))/(2))^(334)+3(-(1)/(2)+(i sqrt(3))/(2))^(365)` का मान होगा
03:58View Solutionयदि कोणांक `(z)lt 0`, तब कोणांक `(-z)` - कोणांक (z) बराबर होगा
03:23View Solutionयदि `z_(1), z_(2)` और `z_(3)` सम्मिश्र संख्याएँ इस प्रकार है कि `|z_(1)|=|z_(2)|=|z_(3)|=|(1)/(z_(1))+(1)/(z_(2))+(1)/(z_(3))|=1` तब `|z_(1)+z_(2)+z_(3)|` है
06:24View Solutionमाना `z_(1)` व `z_(2)` इकाई के n वें मूल है, जोकि मुलबिन्दु पर समकोण बनाते है, तब n निम्न प्रकार का होना चाहिए |
03:06View Solutionसम्मिश्र संख्या `z_(1),z_(2)` और `z_(3)` संतुष्ट करता है। `(z_(1)-z_(3))/(z_(2)-z_(3))=(1-isqrt(3))/(2)` जो उस त्रिभुज के शीर्ष है जो कि:
03:17View Solutionमाना `omega =-(1)/(2)+ i(sqrt(3))/(2)`, तो सारणिक `|(1,1,1),(1,-1-omega^(2),omega^(2)),(1,omega^(2),omega)|` का मान है
04:09View Solutionसभी सम्मिश्र संख्याओं `z_(1), z_(2)`, जो `|z_(1)|=12` और `|z_(2)-3-4i|=5` को सन्तुष्ट करती है, के लिए `|z_(1)-z_(2)|` का न्यूनतम मान है
05:17View Solutionयदि `|z|=1` और `w=(z-1)/(z+1)` (जहाँ `z ne -1`), तब Re (w) है
06:35View Solutionयदि `omega (ne 1)` इकाई का एक घनमूल है और `(1+omega^(2))^(n)=(1+omega^(4))^(n)`, तब n का सबसे छोटा मान है
03:32View Solutionयदि `omega` इकाई का घनमूल हो लेकिन 1 के बराबर हो, तब `|a+bomega+comega^(2)|` का न्यूनतम मान (जहाँ a, b, c पूर्णांक है लेकिन सभी बराबर नहीं) है:
03:41View Solutionछायांकित क्षेत्र, जहाँ `P=(-1,0), Q=(-1+sqrt(2), sqrt(2)), R = (-1+sqrt(2), - sqrt(2))` तथा S = (1,0) को निम्न में से किसके द्वारा प्रदर्शित क्र सकते है ?
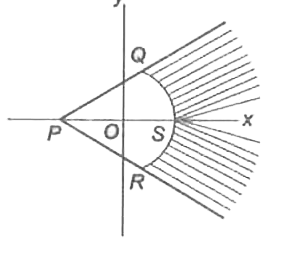 05:06View Solution
05:06View Solutionयदि `w=alpha+ibeta` जहाँ `betane0` तथा `z ne 1` हैं तथा `((w-barwz)/(1-z))` पूर्णतः वास्तविक हैं तब z के मानों का समुच्चय है
07:14View Solutionएक व्यक्ति, मूलबिन्दु से उत्तरपूर्व (N `45^@` E) दिशा में 3 इकाई की दूरी तक चलता है। तत्पश्चात् उत्तर पश्चिम दिशा (N `45^@`W) में 4 इकाई की दूरी तक चलकर बिन्दु P पर पहुँचता है। आर्गण्ड समतल में बिन्दु P की स्थिति है
09:05View Solutionयदि `|z|=1` और `z ne pm 1`, तब `(z)/(1-z^(2))` के सभी मान स्थिति है
04:11View Solutionएक कण P, बिन्दु `z_0 = 1+ 2i` से प्रारंभ होता है, जहाँ `i=sqrt(-1)` सर्वप्रथम यह मूल बिन्दु से क्षैतिज में 5 इकाई दूर जाता है तत्पश्चात् मूल बिन्दु से ऊर्ध्वाधर 3 इकाई की दूरी पर बिन्दु `z_1` पर पहुँचता है। अब कण, `z_1` से सदिश `hati+hatj` की दिशा में `sqrt2` इकाई जाता है तथा तब ये एक वृत्त जिसका केन्द्र मूल बिन्दु है, पर वामावर्त दिशा में `pi/2` कोण से घूम जाता है और एक बिन्दु `z_2` पर पहुँचता है, तब बिन्दु `z_2` है।
03:22View Solutionमाना `z = cos theta + i sin theta `है, तो `theta = 2^@` पर `sum_(m = 1)^(15) Im (z^(2m - 1) )` का मान है
04:52View Solutionमाना `z=x+iy` एक ऐसी सम्मिश्र संख्या है जिसमें `x` व `y` पूर्णांक है। उस आयत का क्षेत्रफल जिसके शीर्ष बिन्दु समीकरण `z bar(z)^(3)+bar(z)z^(3)=350` के मूल है, निम्न है
07:04View Solutionमाना `z` एक सम्मिश्र संख्या है, जिसका काल्पनिक भाग शून्य नहीं है और `a=z^(2)+z+1` वास्तविक है | तब वह मान, जो `a` नहीं ले सकता निम्न है
03:14View Solutionयदि z एक ऐसी सम्मिश्र संख्या है जिसका मापक एक इकाई है तथा कोणांक `theta` है, कोणांक `((1+z)/(1+bar(z)))` बराबर है
03:51View Solutionमाना कि सम्मिश्र संख्याऐं `alpha` तथा `1/(alpha)` क्रमशः वृत्त `(x-x_(0))^(2)+(y-y_(0))^(2)=r^(2)` तथा `(x-x_(0))^(2)+(y-y_(0))^(2)=4r^(2)` पर स्थित हैं। यदि `z_(0)=x_(0)+iy_(0)` समीकरण `2|z_(0)|^(2)=r^(2)+2` को संतुष्ट करता है तब `|alpha|=`
15:23View Solutionमानाकि `w=(sqrt3+i)/2` तथा `P={w^n : n =1,2,3,..}`. इसके अतिरिक्त `H_1={z in C : Re z gt 1/2}` तथा `H_2={z in C : Re z lt 1/2}` , जहाँ C सम्मिश्र संख्याओं का समुच्चय है। यदि `z_1 in P nn H_1, z_2 in P nn H_2` तथा O मूलबिन्दु प्रदर्शित करता है, तब `anglez_1 O z_2`=
17:06View Solutionयदि z एक ऐसी सम्मिश्र संख्या है कि `|z|ge 2` है, तो `|z+(1)/(2)|` का न्यूनतम मान है
05:11View Solutionएक सम्मिश्र संख्या z को एकांक मापांक कहेगे, यदि `|z| =1` हो। माना `z_(1)` तथा `z_(2)` सम्मिश्र संख्याएँ इस प्रकार है की `(z_(1)- 2z_(2))/(2- z_(1) bar(z)_(2))` एकांक मापक है एवं `z_(2)` एकांक मापांक नहीं। तब बिंदु `z_(1)` स्थित होगा
06:23View Solution`theta` का वह एक मान जिसके लिए `(2+3i sin theta)/(1-2i sin theta)` पूर्णतः काल्पनिक है, है
04:18View Solution
बहुविकल्पीय प्रश्न I questions and complete solutions for chapter सम्मिश्र संख्याएँ of JEE MAINS & ADVANCED MATHS (HINDI) of Class 12