Complete Solutions to विश्लेषणात्क प्रश्न of chapter निश्चित समाकलन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | निश्चित समाकलन |
| JEE Main & Advanced (Hindi Medium) | विश्लेषणात्क प्रश्न |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
` int _(0) ^(1) ( t x + 1 - x )^(n) dx ` का मान ज्ञात कीजिए , जहाँ n एक धनात्मक पूर्णांक तथा प्राचल t, x से स्वतंत्र है। अतः प्रदर्शित कीजिए कि `int _(0)^(1) x^(k) (1 - x) ^(n - k) dx = (1)/([""^(n) C_(k) (n + 1)]) , k = 0, 1 , . . . . n ` के लिए होगा।
View Solutionदर्शाइए `int_(0)^(pi)xf(sinx)dx=(pi)/(2)int_(0)^(pi)f(sinx)dx`
View Solutionहल कीजिए `int_(0)^(pi//4)(sinx+cosx)/(9+16sin2x)dx`
View Solutionहल कीजिए `int_(0)^(1//2)(xsin^(-1)x)/(sqrt(1-x^(2)))dx`
View Solutionयदि फलन f(x) आर्वत T में सतत फलन है , तो समाकलन `I = int_(a)^(a+T) f(x)dx`
View Solutionनिम्नलिखित को हल कीजिए
`int_(0)^(pi//2)(xsinxcosx)/(cos^(4)x+sin^(4)x)dx`
View Solutionहल कीजिए
`int_(0)^(pi)(xdx)/(1-cosalphasinx),0ltalphaltpi`
View Solutionफलन `f(x)=int_(1)^(x)[2(t-1)(t-2)^(3)+3(t-1)^(2)(t-2)^(2)]dt` के लिए उच्चिष्ठ तथा निनिम्नस्ष्ठ की जाँच कीजिए।
View Solutionहल कीजिए `int_(0)^(1)log[sqrt(1-x)+sqrt(1+x)]dx`
View Solutionसिद्ध कीजिए कि समाकलन
`int_(0)^(2a)[f(x)//{f(x)+f(2a-x)}]dx` का मान a के बराबर है।
View Solutionयदि f और `g,[0,a]` पर सतत फलन है, जो `f(x)=f(a-x)` तथा `g(x)+g(a-x)=2` को सन्तुष्ट करते है, तो दिखाइए कि
`int_(0)^(a)f(x)g(x)dx=int_(0)^(a)f(x)dx`
View Solutionदिखाइए कि `int_(0)^(pi//2)f(sin2x)sinxdx=sqrt2int_(0)^(pi//4)f(cos2x)cosxdx`
View Solutionहल कीजिए `int_(0)^(pi)(xsin(2x)sin((pi)/(2)cosx))/(2x-pi)dx`
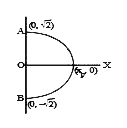
View Solutionयदि 'f' एक संतत् फलन है तथा `int _(0) ^(x) f (t) dt to infty` जब `|x| to infty` हो, तो प्रदर्शित कीजिए कि प्रत्येक रेखा y = m x वक्र `y^(2) + int _(0) ^(x) f (t) dt = 2 ! ` को प्रतिच्छेद करती है।
View Solutionएक तीन घातीय बहुपद `f(x) , x = - 2` पर शून्य हो जाता है तथा उसके `x = - 1 ` एवं `x = 1//3` पर सापेक्षित उच्चिष्ठ एवं निम्निष्ठ है यदि ` int_(-1)^(1) f(x) dx= ( 14)/(3)` हो, तो f(x) ज्ञात कीजिये।
View Solutionएक धन पूर्णाक `nle5` ज्ञात कीजिए, जिसके लिए
`int_(0)^(1)e^(x)(x-1)^(n)dx=16-16e`
View Solutionहल कीजिए `int_(2)^(3)(2x^(5)+x^(4)-2x^(3)+2x^(2)+1)/((x^(2)+1)(x^(4)-1))dx`
View Solutionनिम्न निश्चित समाकलन को हल कीजिए
`int_(-1//sqrt3)^(1//sqrt3)((x^(4))/(1-x^(4)))cos^(-1)((2x)/(1+x^(2)))dx`
View Solution`int_(-pi)^(pi)(2x(1+sinx))/(1+cos^(2)x)dx` का मान ज्ञात कीजिए।
View Solutionनिम्न का समाकलन कीजिए
`int_(0)^(pi//4)log(1+tanx)dx`
View Solutionयदि `(d[f(x)])/(dx) = g (x), a le x le b` , तो `int_(a)^(b) f(x) g (x) dx = `
View Solutionसिद्ध कीजिए कि `int_(0)^(1)tan^(-1)((1)/(1-x+x^(2)))dx=2int_(0)^(1)tan^(-1)xdx` तब और अन्यथा समाकलन `int_(0)^(1)tan^(-1)(1-x+x^(2))dx` को हल कीजिए।
View Solution`int_(0)^(pi)(e^(cosx))/(e^(cosx)+e^(-cosx))dx` को हल कीजिए।
View Solution`xgt0` के लिए, माना `f(x)=int_(1)^(x)(lnt)/(1+t)dt` फलन `f(x)+f(1//x)` को ज्ञात कीजिए और दिखाइए कि `f(e)+f(1//e)=1//2` यहाँ `lnt=log_(e)t`
View Solutionयदि f एक सम फलन है, तो सिद्ध कीजिए कि
`int_(0)^(pi//2)f(cos2x)cosxdx=sqrt2int_(0)^(pi//4)f(sin2x)cosxdx`
View Solutionहल कीजिए
`int_(-pi//3)^(pi//3)(pi+4x^(3))/(2-cos(|x|+(pi)/(3)))dx`
View Solutionहल कीजिए
`int_(0)^(pi)e^(|cosx|){2sin((1)/(2)cosx)+3cos((1)/(2)cosx)}sinxdx`
View Solution`(5050int_(0)^(1)(1-x^(50))^(100)dx)/(int_(0)^(1)(1-x^(50))^(101)dx)` का मान ज्ञात कीजिए।
View Solution
विश्लेषणात्क प्रश्न questions and complete solutions for chapter निश्चित समाकलन of JEE MAINS & ADVANCED MATHS (HINDI) of Class 12