Complete Solutions to विश्लेषणात्मक प्रश्न of chapter सदिश of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सदिश |
| JEE Main & Advanced (Hindi Medium) | विश्लेषणात्मक प्रश्न |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
`A_(1), A_(2), .....,A_(n)`, एक n भुजाओं वाले समबहुभुज (regular polygon ) के शीर्ष हैं 'O' और इसका केन्द्र है। दिखाइए कि
`sum_(i=1)^(n-1)(OA_(i)xxOA_(i+1))=(1-n)(OA_(2)xxOA_(1))3`
View Solution`lambda` के वे सभी मान इस प्रकार ज्ञात कीजिए, कि `x, y, z != (0, 0, 0)` और `(hat(i)+hat(j)+3hat(k))x+(3hat(i)-3hat(j)+hat(k))y+(-4hat(i)+5hat(j))z=lambda(hat(i)x+hat(j)y+hat(k)z)`,
जहाँ `hat(i), hat(j), hat(k)` निर्देशांक अक्षों के अनुदिश इकाई सदिश हैं।
View Solution(a) यदि c एक दिया अशून्य अदिश है और A और B दिए गए अशून्य सदिश इस प्रकार हैं कि `A_|_B` | सदिश X ज्ञात कीजिए , जो समीकरण `A*X=c` और `A xxX=B` को सन्तुष्ट करता है।
(b) एक समकोणीय कार्तीय निर्देशांक निकाय OXYZ में एक सदिश A के घटक `A_(1), A_(2), A_(3)` हैं। निर्देशांक निकाय को `x`-अक्ष के परितः `pi/2` कोण पर घुमाया जाता है। नए निकाय में A के घटक `A_(1), A_(2)` व `A_(3)` के पदों में ज्ञात कीजिए।
View Solutionबिन्दुओं `A, B, C` व `D` के स्थिति सदिश क्रमशः `3hat(i)-2hat(j)-hat(k)`, `2hat(i)+3hat(j)-4hat(k)`,`-hat(i)+hat(j)+2hat(k)` और `4hat(i)+5hat(j)+lambda hat(k)` हैं। यदि बिन्दु `A, B, C` व `D` एक तल में स्थित हैं, तो `lambda` का मान ज्ञात कीजिए।
View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि `|ABxxCD+BCxxAD+CAxxBD|=4` ( त्रिभुज ABC का क्षेत्रफल )
View Solutionमाना कि OACB एक समांतर चतुर्भुज है जहां O मूल बिंदु है तथा OC विकर्ण है। माना कि OA का मध्य बिंदु D है तो सदिश विधि से सिद्ध करो कि BD एवं CO एक दूसरे को समान अनुपात में काटते हैं तथा अनुपात भी ज्ञात करो।
View Solutionयदि सदिश a, b, c समतलीय हैं, तो दिखाइए कि
`|(a,b,c),(a*a,a*b,a*c),(b*a,b*b,b*c)|=0`
View Solutionत्रिभुज OAB में E,OB का मध्य बिंदु है तथा D,AB पर इस प्रकार है कि `AD: DB = 2:1` यदि OD तथा AE बिंदु P पर प्रतिच्छेद करते है, तब अनुपात `OP : PD` सदिश विधि से ज्ञात कीजिए ? ( जहाँ O मूल बिंदु है। )
View Solutionमाना `veca=2hat(i)+hat(k)`, `vecb=hat(i)+hat(j)+hat(k)` और `vecc=4hat(i)-3hat(j)+7hat(k)`, एक सदिश `vecr` ज्ञात कीजिए, जो `vecrxxvecb=veccxxvecb` और `vecr*veca=0` को सन्तुष्ट करता है।
View Solution'c' का मान ज्ञात कीजिए , जिसके लिए सभी वास्तविक x के लिए, सदिश `cxhat(i)-6hat(j)+3hat(k)` और `x hat(i)+2hat(j)+2c x hat(k)` एक -दूसरे से अधिक कोण बनाते हैं।
View Solutionत्रिभुज ABC में BC तथा AC पर क्रमश: बिन्दु D और E इस प्रकार हैं कि BD = 2DC और AE = 3EC है तथा AD और BE का प्रतिच्छेद बिन्दु P है, तो BP/PE का मान सदिश विधि से ज्ञात कीजिए |
View Solutionमाना a, b, c तीन असमतलीय इकाई सदिश हैं, जो एक-दूसरे से समान कोण `theta` बनाते हैं। यदि `axxb+bxxc=p a + q b + rc`, तो अदिश p, q और r का मान `theta` के पदों में ज्ञात कीजिए।
View Solutionचतुर्भुज ABCD के विकर्ण एक -दूसरे को बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि `(AO)/(BO) = (CO)/(DO)` तो सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है ।
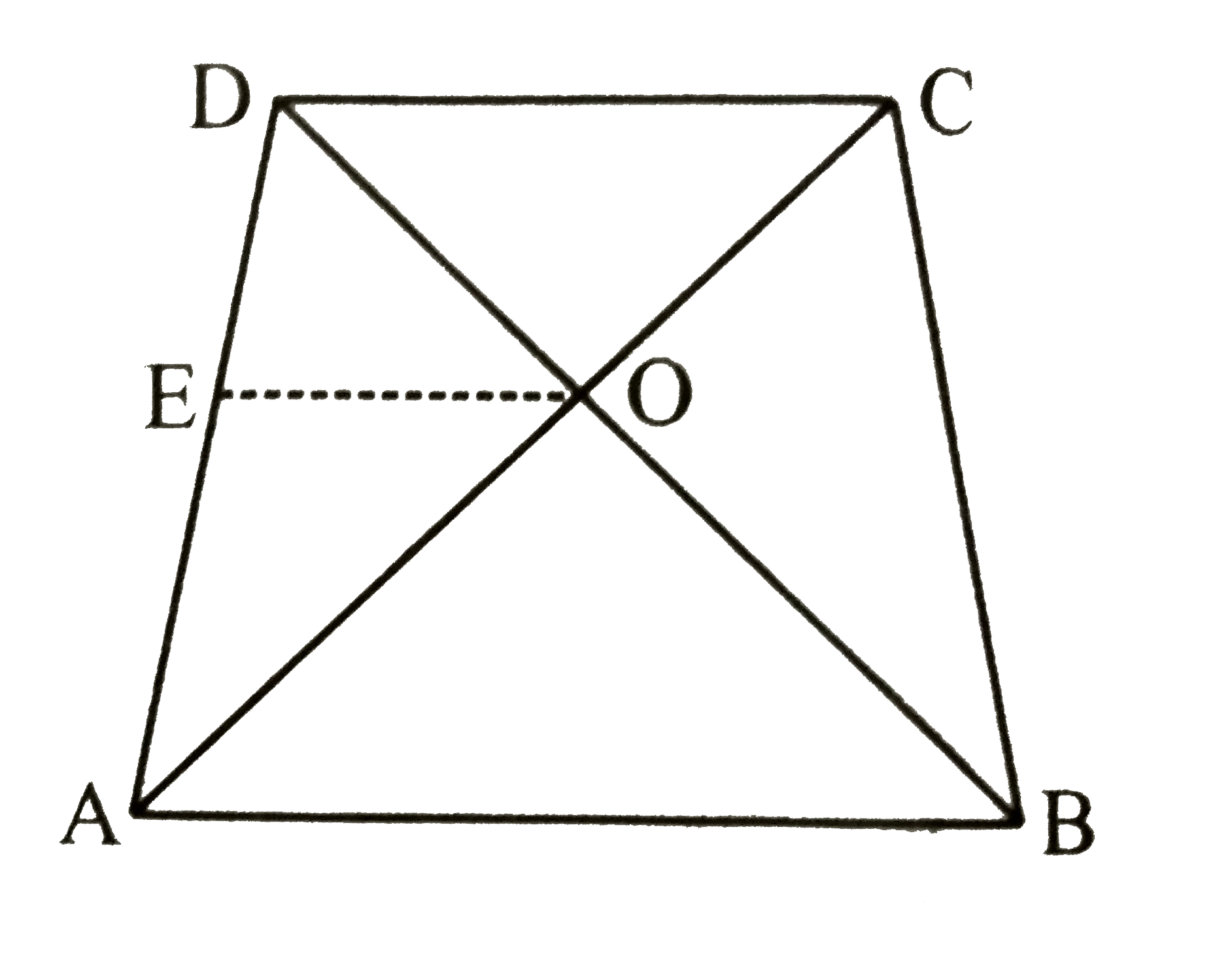
View Solutionयदि `veca,vecb,vecc,vecd` समतलीय सदिश है तो सिद्ध किजिए कि `(vecaxxvecb)xx(veccxxvecd)=vec0`
View Solutionकिसी चतुष्फलक के शीर्ष A,B,C की स्थिति सदिश क्रमशः (1,1,1),(1,0,0) तथा (3,0,0) है। यदि शीर्ष D से विपरीत तल ABC पर लंब डाला जाता है तथा यह त्रिभुज ABC के शीर्ष A से जाने वाली माध्यिका पर बिंदु E पर मिलता है। यदि AD की लम्बाई 4 तथा चतुष्फलक का आयतन `(2sqrt(2))/3` है। तो E की स्थिति ज्ञात कीजिए।
View Solutionयदि सदिश A, B और C इस प्रकार हैं कि `|B|=|C|, [(A+B)xx(A+C)]xx(BxxC)*(B+C)=0` सिद्ध कीजिए कि
View Solutionकिन्हीं दो सदिश `vec(u)` तथा `vec(v)` के लिए, निम्न सिद्ध कीजिए
(a) `(vec(u).vec(v))^(2)+|vec(u)xx vec(v)|^(2)=|vec(u)|^(2)|vec(v)|^(2)`
(b)` (1+|vec(u)|^(2))(1+|vec(v)|^(2))=(1-vec(u).vec(v))^(2)+|vec(u)+vec(v)+(vec(u)xx vec(v))|^(2)`
View Solutionमाना `vec(u)` तथा `vec(v)` इकाई सदिश है | यदि सदिश `vec(w)` इस प्रकार है कि `vec(w)+(vec(w)xx vec(u))=vec(v)`, तो सिद्ध कीजिए कि `|(vec(u)xx vec(v)).vec(w)|lt(1)/(2)` तथा असमिका तभी सन्तुष्ट होगी, यदि और केवल यदि `vec(u),vec(v)` के लम्बवत हो |
View Solutionसिद्ध कीजिए कि त्रिभुज की शीर्षों से सम्मुख भुजाओं पर डाले गये लम्ब संगामी होते हैं |
View Solutionसिद्ध कीजिए कि त्रिभुज की शीर्षों से सम्मुख भुजाओं पर डाले गये लम्ब संगामी होते हैं |
View Solutionत्रिविमीय सदिश `vecv_(1), vecv_(2), vecv_(3)` ज्ञात कीजिए , जो `vecv_(1)*vecv_(1)=4`, `vecv_(1)*vecv_(2)=-2`, `vecv_(1)*vecv_(3)=6`, `vecv_(2)*vecv_(2)=2`, `vecv_(2)*vecv_(3)=-5`, `vecv_(3)*vecv_(3)=29` को सन्तुष्ट करते हैं।
View Solutionमाना कि `vecA(t)=f_(1)(t)hati+f_(2)(t)hatj` तथा `vecB(t)=g_(1)(t)hati+g_(2)(t)hatj,t in [0,1]` है जहां `f_(1),f_(2),g_(1),g_(2)` सतत फलन हैं यदि `vecA(t)` और `vecB(t)` सभी t के लिए अशून्य सदिश है और `vecA(0)=2hati+3hatj, vecA(1)=6hati+2hatj, vecB(0)=3hati+2hatj` एवं `vecB(1)=2hati+6hatj` हो तो प्रदर्शित कीजिए कि कुछ t के लिए `vecA(t)` और `vecB(t)` समांतर है।
View Solutionमाना V सदिशों
`a=a_(1)i+a_(2)j+a_(3)k`
`b=b_(1)i+b_(2)j+b_(3)k`
`c=c_(1)i+c_(2)j+c_(3)k`
द्वारा बने समान्तर षट्फलक का आयतन है। यदि `a_(r ), b_(r ), c_(r )`, जहाँ `r=1,2,3` अऋणात्मक वास्तविक संख्याएँ है और `sum_(r=1)^(3)(a_(r )+b_(r )+c_(r ))=3L` तो
View Solutionयदि u, v, w तीन असमतलीय इकाई सदिश हैं और `alpha, beta, gamma` क्रमशः u और v, v और w, w और u के बीच के कोण हैं और x, y, z क्रमशः `alpha, beta, gamma` के लम्बअर्द्धकों की दिशा में इकाई सदिश हैं। सिद्ध कीजिए कि
`[(x xx y, y xx z ,z xx x)]=1/16 [(u, v, w)]^(2)sec^(2). (alpha)/(2) sec^(2). (beta)/(2) sec^(2). (gamma)/(2)`.
View Solutionयदि a, b, c, d चार भिन्न सदिश हैं , जो प्रतिबन्धों `a xx b= c xx d` और `a xx c = b xx d ` को सन्तुष्ट करते हैं, तो `a*b+c*d != a * c + b*d` सिद्ध कीजिए कि
View Solutionआवर्तित किरण इकाई सदिश `hat(v)` के अनुदिश तथा परावर्तित किरण इकाई सदिश `hat(w)` के अनुदिश है। अभिलम्ब इकाई सदिश `hat(a)` के अनुदिश बाहर की तरफ है। `hat(w)` को `hat(a)` और `hat(v)` के पदों में व्यक्त कीजिए।
View Solution
विश्लेषणात्मक प्रश्न questions and complete solutions for chapter सदिश of JEE MAINS & ADVANCED MATHS (HINDI) of Class 12
All Exercises from JEE Main & Advanced (Hindi Medium) Class 12 MATHS सदिश
- एकल पूर्णांक प्रश्न
- दृढ़कथन-कारण प्रकार (प्रश्न में वक्तव्य I ( दृढ़कथन ) और वक्तव्य II ( कारण ) दिए गए हैं। प्रश्न के चार विकल्प (a), (b), (c) तथा हैं, जिनमें से केवल एक सही है। )
- बहुविकल्पीय प्रश्न I ( केवल एक विकल्प सही है )
- बहुविकल्पीय प्रश्न II ( एक से अधिक विकल्प सही हैं )
- मैट्रिक्स सुमेल -प्रकार
- रिक्त स्थानों की पूर्ति कीजिए
- विश्लेषणात्मक प्रश्न
- सत्य/असत्य