Complete Solutions to ADDITIONAL EXERCISES of chapter NUCLEI of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEI |
| NCERT GUJARATI | ADDITIONAL EXERCISES |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are `""_(12)^(24)Mg (23.98504u), ""_(12)^(25)Mg (24.98584u) and ""_(12)^(26)Mg (25.98259u)`. The natural abundance of `""_(12)^(24)Mg` is 78.99% by mass. Calculate the abundances of other two isotopes.
03:35View SolutionThe neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei `""_(20)^(41)Ca and ""_(13)^(27)Al` from the following data:
`m(""_(20)^(40)Ca) = 39.962591 u`
`m(""_(20)^(41)Ca) = 40.962278 u`
`m(""_(13)^(26)Al) = 25.986895 u`
`m (""_(13)^(27)Al) = 26.981541 u`.05:18View SolutionA source contains two phosphorous radio nuclides `""_(15)^(32)P (T_(1//2) = 14.3d)` and `""_(15)^(33)P(T_(1//2) = 25.3d)`. Initially, 10% of the decays come from `""_(15)^(33)P`. How long one must wait until 90% do so?
06:08View SolutionUnder certain circumstances, a nucleus can decay by emitting a particle more massive than an a-particle. Consider the following decay processes:
`""_(88)^(223)Ra to ""(82)^(209)Pb + ""_(6)^(14)C`.
`""_(88)^(223)Ra to ""_(86)^(219)Rn + ""_(2)^(4)He`
Calculate the Q-values for these decays and determine that both are energetically allowed.03:53View SolutionConsider the fission of `""_(92)^(238)U` by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are `""_(58)^(140)Ce` and `""_(44)^(99)Ru`. Calculate Q for this fission process. The relevant atomic and particle masses are
`m(""_(92)^(238)U) =238.05079 u`
`m( ""_(58)^(140)Ce ) =139.90543 u`
`m(""_(44)^(99)Ru ) = 98.90594 u`03:39View SolutionConsider the D–T reaction (deuterium–tritium fusion)
`""_(1)^(2)H + ""_(1)^(3)H to ""_(2)^(4)He + n`
(a) Calculate the energy released in MeV in this reaction from the data:
`m (""_(1)^(2)H) = 2.014102u`
`m(""_1^(3)H) = 3.016049 u`
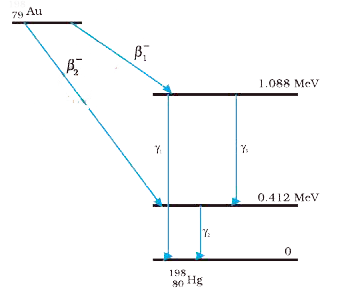
(b) Consider the radius of both deuterium and tritium to be pproximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2), k = Boltzman’s constant, T = absolute temperature.)06:04View SolutionObtain the maximum kinetic energy of b-particles, and the radiation frequencies of g decays in the decay scheme shown in Fig. You are given that
`m(""_(8)^(19)Au) = 197.968233 u`
`m(""_(8)^(19)Hg) =197.966760 u`.
 View Solution
View SolutionCalculate and compare the energy released by a) fusion of 1.0 kg of hydrogen deep within Sun and b) the fission of 1.0 kg of `""^(235)U` in a fission reactor.
04:14View SolutionSuppose India had a target of producing by 2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i.e. conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission of 235U to be about 200MeV.
07:45View Solution
ADDITIONAL EXERCISES questions and complete solutions for chapter NUCLEI of NCERT PHYSICS(GUJRATI) of Class 12
