Complete Solutions to प्रश्नावली 9.4 of chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| NCERT EXEMPLAR HINDI | प्रश्नावली 9.4 |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
किसी समांतर चतुर्भुज `ABCD` की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती है। सिद्ध कीजिए कि ar `(ADF) = ar (ABFC)` है।
06:37View Solutionएक समांतर चतुर्भुज ABCD के विकर्ण बिंदु O पर प्रतिच्छेद करते है। O से होकर एक रेखा खींची जाती है, जो AD को P और BC से Q पर मिलती है। दर्शाइए कि PQ इस समांतर चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागो में विभाजित करता है।
07:36View Solutionएक त्रिभुज ABC की माध्यिकाएँ BE और CF परस्पर बिंदु G पर प्रतिच्छेद करती है। सिद्ध कीजिए कि `DeltaGBC` का क्षेत्रफल चतुर्भुज AFGE के क्षेत्रफल के बराबर है।
06:24View Solutionआकृति में, `CD||AE` और `CY||BA` है। सिद्ध कीजिए कि `ar (CBX) = ar (AXY)` है।
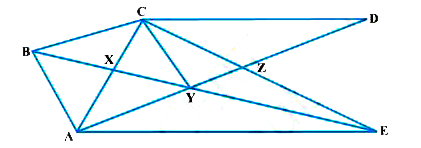 03:14View Solution
03:14View SolutionABCD एक समलंब है, जिसमे `AB||DC, DC=30cm` और `AB=50cm` है। यदि X और Y क्रमशः AD और BC के मध्य-बिंदु है, तो सिद्ध कीजिए कि ar (DCYX) = `(7)/(9)` ar (XYBA) है।
03:58View Solutionत्रिभुज `ABC` में यदि L और M क्रमशः AB और AC भुजाओ पर इस प्रकार स्थित बिंदु है कि `LM||BC` है। सिद्ध कीजिए कि `ar (LOB) = ar (MOC)` है।
03:12View Solutionआक्रति 9.27 में ABCDE एक पंचभुज है । B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है दर्शाइए कि
`(i) ar (ACB)=ar(ACF)`
`(ii) ar=(AEDF) =ar(ABCDF)`
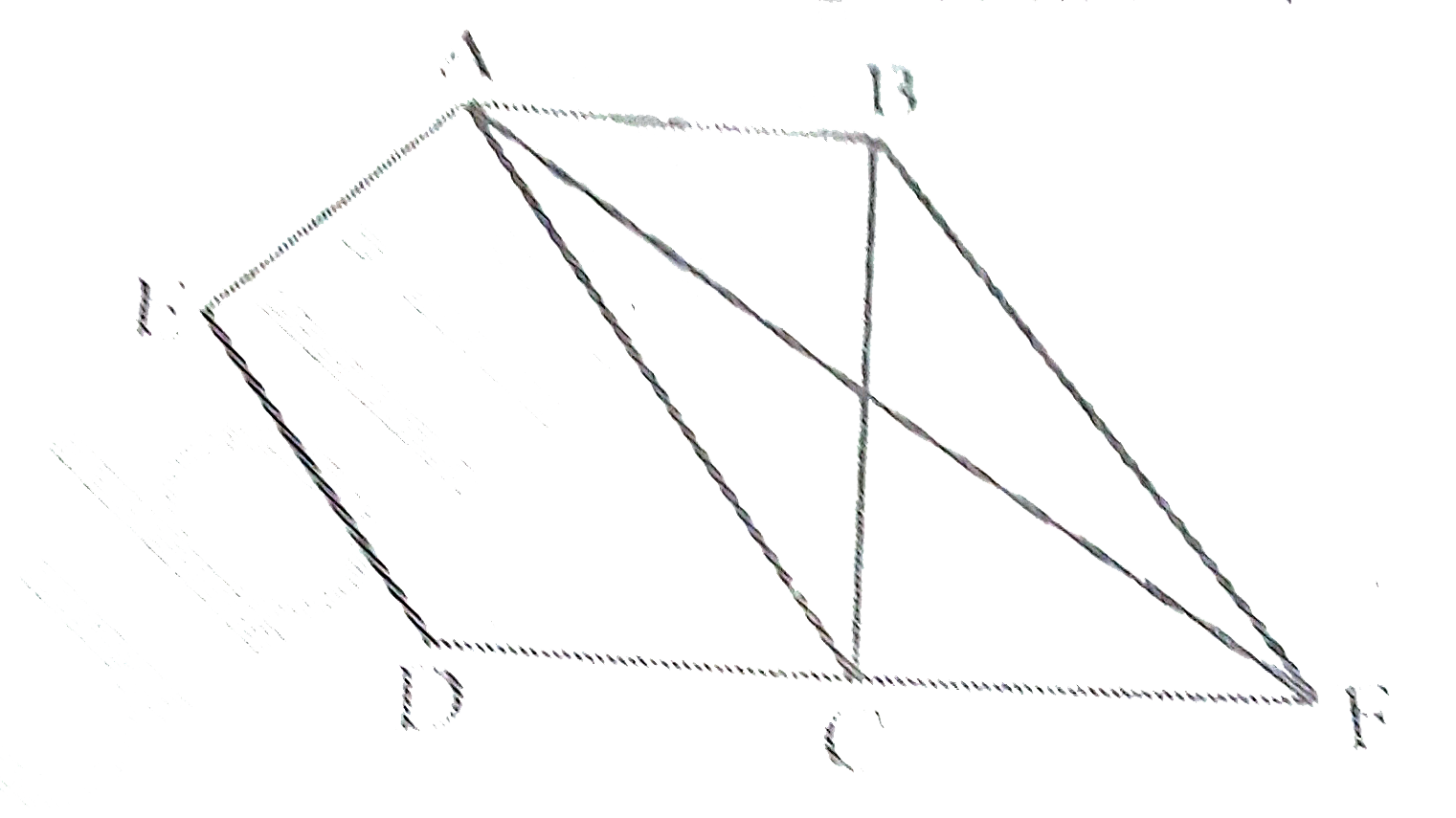 03:58View Solution
03:58View Solutionयदि एक त्रिभुज ABC की माध्यिकाएँ G पर मिलती है, तो सिद्ध कीजिए कि ar (AGB) = ar (AGC) = ar (BGC)= `(1)/(3)` ar (ABC) है।
06:00View Solutionआकृति में, X और Y क्रमशः AC और AB के मध्य-बिंदु है, `QP||BC` और CYQ और BXP सरल रेखाएँ है। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) है।
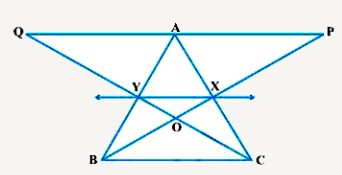 04:57View Solution
04:57View Solutionआकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज है। दर्शाइए कि ar (ADE) = ar (BCF) है।
 05:28View Solution
05:28View Solution
प्रश्नावली 9.4 questions and complete solutions for chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of NCERT EXEMPLAR HINDI of Class 9
