Complete Solutions to QUESTION BANK of chapter AREA of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
Draw a circle and a triangle with one vertex at the center of the circle and the other two on the circle. Draw another triangle of the same area with all three vertices on the circle.
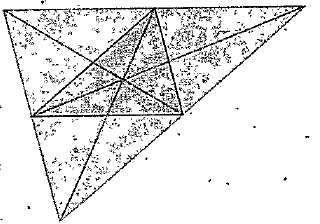
View SolutionIn the picture below, the lines parallel to each side of the blue triangle through the opposite vertex are drawn to make the big triangle. How many triangles in the picture have the same area as that of the blue triangle? How many of them have the same measures of the blue triangle?
View SolutionProve that the two triangles shown below have the same area:
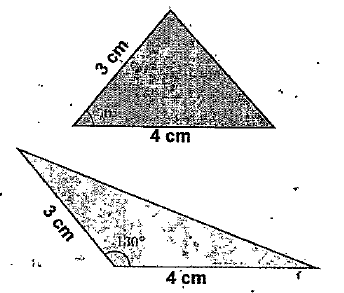 .
.
View SolutionHow many different triangles of the same area can be drawn without changing the lengths of two sides?
View SolutionDraw triangle having sides 6cm, 7cm and 8 cm. Draw an isosceles triangle of the same area with one side 8cm.
View SolutionDraw triangle having sides 4,5,7 centimetres. Draw three different triangles of the same area.
View SolutionDraw Delta A B C having two sides 5cm and 6 cm and angle between these two sides 60^0. Draw three triangles of the same area with measurements `angle A C R=30^0, angle B C Q=60^0` and `angle B A P =90^0`.
View SolutionDraw triangle having one side 7 cm and angle at its ends are `30^0` and `40^0`. Draw three isosceles triangles of the same area.
View SolutionDraw triangle having two sides 6 centimetres and 5 centimetres and angle between these two. sides `60^0.` Draw a triangle of the same. area. wịh sides 6 cm and 5 cm 'but not equal to the first triangle.
View SolutionDraw a circle and a triangle with one vertex at the center of the circle and the other two on the circle. Draw another triangle of the same area with all three vertices on the circle.
View SolutionDraw a quadrilateral, a pentagon and a hexagon In GeoGebra and draw triangles of the same areas.
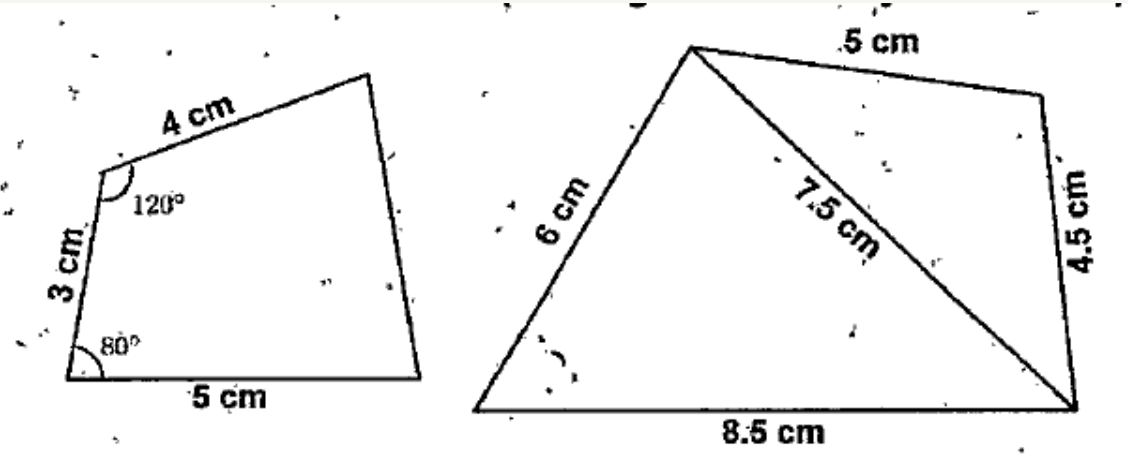
View SolutionDraw the two rilaterals shown below, in your note book. Draw triangles of the same area and calculate the areas (The lengths needed may be measured).
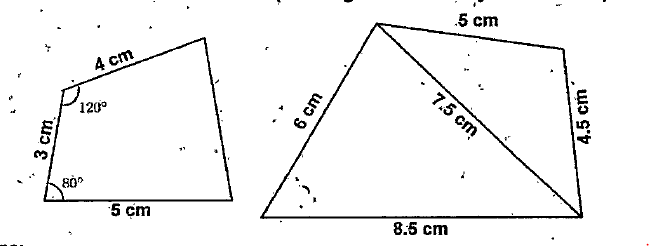
View SolutionDraw a rhombus of sidies 6 centimetres and one` angle60^0`, then draw a triangle of the same area.
View SolutionDraw a. regular pentagon and then. a triangle of the same area. Calculate the area
View SolutionThe picture shows a rectangle divided into two parts.
Instead of the broken line separating these parts, draw a straight line to divide the rectangle into two other parts of the same area. Calculate the areas ofthese parts.
View SolutionIn the figure ABCD is a trapezium. Diagonal AC and BD intersect at O. Area of triangle A B C is 24 cm^2 and area of triangle AOB is 10 sq.cm.
a) Find the area of triangle BOC.
b) How much is the area of triangle AOD? Write reason.
View SolutionDraw the rilaterai with given measures. Draw a triangle of the same area as that of the rilateral.
View SolutionIn the picture below, the lines, parallel to side of triangle A B C through the оррosite vertex are drawn to make the triangle PQR.
a) Draw this picture, Draw the lines BQ, CP and AR.
b) The triangles. ABP, AQC and BRC have the same arẹa as that of triangle A B C. Why?
c) Find another 4 triangles of same area as that of triangle A B C from the picture which you have drawn and write their names.
View SolutionDrạw a regular pentagon having side 4 centimetre and draw a triangle of same area. Find the area of the triangle.
View SolutionIn the picture below, two lines are drawn from the top vertex of a triangle to the bottom side:
Prove that the ratio in which these lines divide the length of the bottom side is equal to the ratio of the area of the three smaller triangles in the picture.
View SolutionIn the picture below, the top vertex of a triangle is joined to the midpoint of the bottom side of the triangle and then the midpoint of this line is joined to the other two vertices.
Prove that the areas of all four triangles obtained thus are equal to a fourth of the area of the whole triangle.
View SolutionIn the picture below, the top vertex of a triangle is joined to the midpont of the opposite side and then the point dividing this line in the ratio 2:1 is joined to the other two vertices:
Prove that the areas of all three triangles in the picture on the are equal to a third of the area of the whole triangle.
View SolutionProve that the lengths of the perpendiculars from any point on the bisector of an angle to the sides are equal.
View SolutionIn the picture below, the side AC of the triangle ABC is extended by D, by adding the length of the side CB. Then the line through C parallel to DB is drawn to meet AB at E.
Prove that CE bisects
`angle C`

View SolutionIn the figure, the diagonals of a quadrilateral split it into four triangles. The areas of three of them are shown in the picture:
Calculate the area of the whole quadrilateral.
View SolutionIn this picture the horizontal lines at the top and bottom are parallel. Prove that the yellow and red triangles are of the same area.
View SolutionIn the figure, the diagonals of a trapezium split into four triangles.
The area of the yellow triangle is 10 square centimetres and the area of the green triangle is 20 square centimetres. What is the area of the whole trapezium?
View SolutionThe picture below shows a trapezium divided into four parts by the diagonals.
The area of thé blue triangle is 4 square centimetres and the area of the green triangle is 9 square centimetres. What is the fotal area of the trapezium?
View SolutionDraw a square of sides 5 centimetres. Draw an isosceles triangle of the same area.
View SolutionProve that the two triangles shown below have the same area
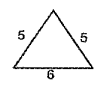
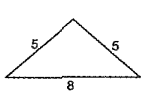
View SolutionIn triangle ABC, D is the.midpoint of BC and E is the midpoint of BD. Also O is the midpoint of AE. Prove that area of triangle ABC is 8 X the area of triangle BOE.
View SolutionIn the figure ABCD is a rectangle and P is a point on the side CD. Prove that the area of triangle A Q B is equal to the sum of the areas of triangle P Q D and Delta P C B.
View SolutionA rectangular field is divided into 8 plots by drawing two triangles, In eight plots four varities (ginger, beans, paddy, gingelly) are cultivated. Each is indicated in the following shades.
Prove that the area of ginger is equal to the area of beans, and also prove that area of the paddy is equal to the area. of gingelly.
View SolutionIn parallelogram ABCD, P and Q are the points on the sides A B and C D. Lines AQ.and PD are intersect in K and Ifhes PC and BQ are intersect in L. Prove that the area of the rilateral PKQL is equal to the sum of the areas of the triangle A K D, Delta B L C
View SolutionConstruct a angled triangle.such that its hypotenuse being 12 centi-metres and area being 24 square centime-, tres.
View SolutionLook at these pictures:
The rilateral ABCD is transformed to the triangle ADE of equal area. The side AD of the rilateral is also'a side of the triangle. Can ypu similarly draw triangles of equal area, sharing the other sides of the rilateral?
View SolutionIn the figure ABCD is a rectangle. AB= 6 cm, BC=4 cm . P is the midpoint of CD.
a) What is the area of triangle APB?
b) What is the area of triangle PAD?
c) If AQ: Q B=1: 2, then what is the area of the quadrilateral AQPD?
View SolutionIn the figure, B P: P Q: Q C=1: 2: 1. Area of triangle APQ is 8 sq.cm.
(a) Find the area of triangle A B P.
b) Find the area of triangle ABC.
View SolutionIn the figure, BC=12 cm, BD=3 cm. Area of triangle ABC is 80 sq.cm.
a) What is BD : DC?
b) Find the area of triangle ADC.
View SolutionIn the figure, the line CE is parallel to BD. Area of triangle A B D is 30 sq.cm. and that of triangle BDC is 29 sq . cm.
a) What is the area of quadrilateral ABCD?
b) What is the area of triangle BED?
c) What is the area of quadrilateral ABED?
View SolutionIn the figure, B D=D C, P A=P D. Area of triangle A B C is 100 sq.cm.
What is the area of triangle PAB?
View SolutionIf AB=8 cm, AC=6 cm BC=9 cm. AD is the bisector of angle A.
a) B D: D C=
b) What is the ratio of areas of triangle ABD and triangle ACD?
View SolutionIn the figure, Area of rectangle ABGD is 36 sq.cm. What is the area of triangle ABP?
View SolutionIn the figure, AB=12 cm AD=4 cm. Then
a) BD=---- cm.
b) The ratio of the areas of triangle ADC and triangle BDC is =…….
View SolutionArea of triangle BPC is 10 sq.cm.
a) Find the area of triangle A B C.
b) Find the area of rectangleABCD.
View SolutionDraw triangle having sides 5 ~cm, 6 ~cm and 7 ~cm. Draw an isosceles triangle of the same area and having one side beginarraylll 7 cm.
View SolutionIn the figure, A B C D is a trapezium. Diagonal A C and B D intersect at M. Area of triangle ABC is 24 cm^2 and area of triangle AMB is 10cm^2.
a) Find the area of triangle BMC.
b) How much is the area of triangle AMD? Write reason.
View SolutionDraw a rilateral with given measures. Draw a triangle of the same area as that of the rilateral.
View SolutionDraw a rergular pentagon having side 4 ~cm and draw a triangle of the same area.
View SolutionIn triangle ABC, AM is the bisector of angle BAC. MP is drawn perpendicular to AB and MQ is perpendicular to AC.
a) Prove that MP,and MQ are of the same length.
b) Prove that, in any triangle, the bisector of an angle divides the oppositè sidein the ratio of the sides of the angle.
View SolutionIn the figure, line AB is parallel to CD. AB=5 cm , AC=4 cm, angle CAB=`90^circ`.
a) Calculate the area of triangle ABC.
b) How much is the area of triangle ABD? Write reason.
View SolutionIn the picture below, the lines, parallel to side of triangle A B C through the оррosite vertex are drawn to make the triangle PQR.
a) Draw this picture, Draw the lines BQ, CP and AR.
b) The triangles. ABP, AQC and BRC have the same arẹa as that of triangle A B C. Why?
c) Find another 4 triangles of same area as that of triangle A B C from the picture which you have drawn and write their names.
View SolutionDraw triangle ABC with AB=8 ~cm_-3 B C=6 ~cm . and angle B=30^0. Draw a angled triangle of the same area. Measure its perpendicular. sides. Calculate the area of the triangle.
View SolutionIn the figure, Area of rectangle ABGD is 36 sq.cm. What is the area of triangle ABP?
View SolutionIn the figure, AB=12 cm AD=4 cm. Then
a) BD=---- cm.
b) The ratio of the areas of triangle ADC and triangle BDC is =…….
View SolutionIn the figure, line AB is parallel to CD. AB=5 cm , AC=4 cm, angle CAB=`90^circ`.
a) Calculate the area of triangle ABC.
b) How much is the area of triangle ABD? Write reason.
View SolutionIn the figure A B is parallel to CD. Write the pairs of triangles having the same area.
View SolutionIn the triangle ABC, AB=9 centimetres, B C=12 centimetres. The line B D is the bisector of angle B. What is the ratio of the areas of triangle A B D and triangle B C D ?
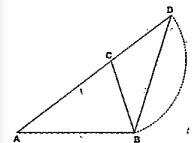
View SolutionAB is the diameter of thecircle and C is a point on thecircle.
. i) Draw a rough figüre like this and draw another triangle with all vertices lying on thecircle and area equal to the areà of triangle, ABC.
ii) Draw an isosceles triangle of same area.
View SolutionIn the figure the area of triangle APB is 25 square centimetres. What is the area of triangle ABC ? What is the area of rectangle ABCD?
View SolutionIn rectangle PQRS, O is the midpoint of QR. Area of POQ is 16 sq. cm.
a) What is the area of POS?
b) What is the area of OSR?
c) Find the area of the rectangle PQRS?
View Solution
QUESTION BANK questions and complete solutions for chapter AREA of V PUBLICATION of Class 9