SANJEEV PUBLICATION दोलन की गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न कक्षा 11 के लिए

कक्षा 11	भौतिकी
Chapter	दोलन
SANJEEV PUBLICATION	गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न
माध्यम	हिंदी
शैक्षणिक वर्ष	2023-2024

Question 1
दो विस्थापनों $y_{1}$ = a sin $(ω t)$ तथा y = b cos (Ot) के अध्यारोपण से प्राप्त परिणामी गति--हल देखें
Question 2
एक कण A आयाम से सरल आवर्त दोलन कर रहा है। जब यह अपने मूल स्थान से $\frac{2 A}{3}$ पर पहुँचता है, तब अचानक इसकी गति तिगुनी कर दी जाती है। तब इसका नया आयाम है हल देखें
Question 3
यदि किसी सरल रेखा के अनुदिश सरल आवर्त गति करते हुए किसी कण की मूल बिन्दु से दूरी $x_{1}$ , तथा $x_{2}$ , होने पर उसका वेग क्रमशः $V_{1}$ , तथा $V_{2}$ , है, तो इस कण का आवर्तकाल है-हल देखें
Question 4
सरल आवर्त गति करते हुए किसी कण का अधिकतम त्वरण $α$ तथा अधिकतम वेग $β$ है, तो कम्पन्न का आवर्तकाल होगा हल देखें
Question 5
कोई कण इस प्रकार गति करता है कि उसका त्वरण समीकरण $α$ = -bx द्वारा प्रदर्शित किया जाता है, जिसमें x सन्तुलन स्थिति से विस्थापन तथा b कोई नियतांक है। दोलनकाल होगा हल देखें
Question 6
एक कण एक सरल रेखा में सरल आवर्त गति से गतिशील है। यह विरामावस्था से प्रारम्भ कर प्रथम $τ$ सेकण्ड में दूरी a और अगले $τ$ सेकण्ड में दूरी 2a उसी दिशा में तय करता है। तब हल देखें
Question 7
धनात्मक (+ ve) x-दिशा में चलती हुई किसी तरंग की y-दिशा में विस्थापन 1 m, तरंगदैर्घ्य $2 π$ m है तथा इसकी आवृत्ति $\frac{1}{π}$ Hz है। इस तरंग के लिए सही समीकरण होगा हल देखें
Question 8
किसी एक समान तार के अनुप्रस्थ काट का क्षेत्रफल A है। इससे बनाये गये एक लोलक का आवर्तकाल T है। इस लोलक के गोलक से एक अतिरिक्त M द्रव्यमान जोड़ देने से लोलक का आवर्तकाल परिवर्तित होकर $T_{M}$ , हो जाता है। यदि इस तार के पदार्थ का यंग गुणांक Y हो, तो $\frac{1}{Y}$ का मान होगा (g = गुरुत्वीय त्वरण)-हल देखें
Question 9
कोई लोलक एक काफी ऊँचे भवन की छत से लटका है और सरल आवर्त दोलक की भाँति मुक्त रूप से आगे-पीछे गति कर रहा है। माध्य स्थिति से 5 m की दूरी पर इसके गोलक का त्वरण 20 m/ $s^{2}$ है। दोलन का आवर्तकाल है हल देखें
Question 10
क क्षैतिज कमानी से बंधा एक द्रव्यमान M आयाम $A_{1}$ , से सरल आवर्त गति कर रहा है। जब द्रव्यमान M अपनी माध्य अवस्था से गुजर रहा है, तब एक छोटा द्रव्यमान m इसके ऊपर रख दिया जाता है और अब दोनों आयाम $A_{2}$ , से गति करते हैं। $(\frac{A_{1}}{A_{2}})$ अनुपात है हल देखें
Question 11
किसी कमानी का ऊपरी सिरा स्थिर है तथा निचले सिरे से m द्रव्यमान का एक पिण्ड लटका है। कमानी का अपना द्रव्यमान नगण्य है। कमानी के निचले सिरे को थोड़ा-सा खींचकर छोड़ देने पर द्रव्यमान m का पिण्ड दोलन करने लगता है और इसके दोलनों का आवर्तकाल 3 s होता है। m के मान में 1 kg बढ़ाने पर दोलनों का आवर्तकाल 5 s हो जाता है। m का kg में मान हल देखें
Question 12
एक स्प्रिंग (कमानी) का कमानी स्थिरांक k है। इसको तीन भागों में काट दिया गया है जिनकी लम्बाइयों का अनुपात 1 : 2 : 3 है। इन तीनों भागों को श्रेणीक्रम में जोड़ने पर संयोजन का कमानी स्थिरांक K' तथा समान्तर क्रम में जोड़ने पर K" है, तो अनुपात K' : K" होगा-हल देखें
Question 13
लम्बाई L व द्रव्यमान M की एकसमान छड़ अपने केन्द्र पर कीलित है। इस छड़ के सिरों पर k स्प्रिंग नियतांक के एक जैसे स्प्रिंग लगे हैं जिनके दूसरे सिरे दृढ़ आलम्बों से जुड़े हैं। छड़ क्षैतिज तल में स्वतन्त्र रूप से दोलन कर सकती है। छड़ को एक छोटे कोण $θ$ से घुमाकर छोड़ दिया जाता है। छड़ के दोलन की आवृत्ति होगी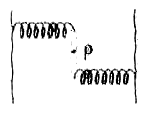
हल देखें
Question 14
सरल आवर्त गति करते किसी कण का विस्थापन y= $A_{0} + A sin ω t + B cos ω t$ द्वारा निरूपित किया गया है। तब इसके दोलन का आयाम होगा हल देखें
Question 15
एक पूर्ण दोलन में सरल आवर्त गति करते किसी कण का औसत वेग होता है हल देखें
Question 16
3 kg द्रव्यमान का एक ठोस सिलिण्डर (बेलन) किसी क्षैतिज समतल पर 4 m $s^{- 1}$ के वेग से लुढ़क रहा है। यह 200 Nm^(-1) के बल नियतांक के एक क्षैतिज स्प्रिंग (कमानी) से टकराता है, तो स्प्रिंग से उत्पन्न अधिकतम संपीड़न होगा हल देखें
Question 17
एक ऊर्ध्वाधर बेलनाकार पात्र में रखी एक आदर्श गैस एक द्रव्यमान M के स्वतंत्र रूप से गतिशील पिस्टन को आधार देती है। पिस्टन और बेलन के अनुप्रस्थ परिच्छेद क्षेत्रफल एकसमान A हैं। जब पिस्टन साम्यावस्था में है, तब गैस का आयतन $V_{0}$ , है और इसका दाब $P_{0}$ है। पिस्टन को इसी साम्यावस्था स्थिति से थोड़ा-सा विस्थापित किया जाता है और फिर छोड़ दिया जाता है। यह मान लें कि निकाय अपने परिवेश से पूर्णतः रोधी है तब पिस्टन इस आवृत्ति की सरल आवर्त गति करेगा हल देखें
Question 18
एक द्रव्यमान-रहित स्प्रिंग की तनाव-रहित लम्बाई 4.9 m है। उसका एक सिरा बंधित है और दूसरे पर एक छोटा गुटका लगा है (चित्र देखिये)। यह निकाय एक घर्षण-रहित क्षैतिज (horizontal) सतह पर रखा है। समय 1 = 0 पर गुटके को 0.2 m खींचकर स्थिर अवस्था से छोड़ा जाता तब वह गुटका $ω = \frac{π}{3} r o \frac{d}{s}$ आवृत्ति का सरल-आवर्त-दोलन करता है। ठीक उसी समय (t = 0) पर छोटा कंकड़ । चाल से क्षैतिज से $45^{\circ}$ कोण पर बिन्दु P से प्रक्षेपित किया जाता है। बिन्दु P की बिन्दु 0 से दूरी (क्षैतिज) 10 m है। यदि t= 1s पर कंकड़ गुटके पर गिरता है, तब v का मान है (g = 10 m/ $s^{2}$ लें)
हल देखें
Question 19
किसी ठोस में चाँदी की एक परमाणु $10^{12}$ /sec की आवृत्ति से किसी दिशा में सरल आवर्त गति करता है। एक परमाणु को दूसरे परमाणु से जोड़ने वाले बंध का बल नियतांक कितना होगा? (चाँदी का आण्विक भार = 108 और अवागाद्रो (Avagadro) संख्या = 6.02 $\times 10^{23}$ gm $m o \leq^{- 1}$ )हल देखें
Question 20
चिकनी सतह पर रखे m द्रव्यमान के एक गुटके को स्प्रिंग नियतांक k की एक कमानी (जिसका द्रव्यमान नगण्य है) से जोड़ा गया है। कमानी का दूसरा सिरा चित्रानुसार, अचल है। आरम्भ में गुटका अपनी साम्यावस्था में स्थायी है। यदि गुटके को एक नियत बल F से खींचा जाये तो गुटके की अधिकतम चाल होगी
हल देखें
Question 21
एक कण 5 cm आयाम से सरल आवर्त गति कर रहा है। जब कण अपनी मध्य स्थिति से 4 cm दूरी पर है तब इसके वेग से परिमाण SI मानकों में इसके त्वरण में परिमाण के बराबर है तो कण का सेकण्ड में आवर्तकाल होगा हल देखें
Question 22
एक प्रगामी आवर्ती तरंग को समीकरण y(x, y) = $10^{- 3}$ sin(50t + 2x) से निरूपित किया जाता है, जहाँ x तथा y मीटर में तथा 1 सेकण्ड में हैं। निम्न में से तरंग के लिए कौनसा कथन सत्य है|हल देखें
Question 23
एक सरल दोलक, जो कि $l$ लम्बाई की डोरी तथा m द्रव्यमान के गोलक से बना है, को एक छोटे कोण $θ_{0}$ से छोड़ा जाता है। यह गोलक एक द्रव्यमान M के गुटके को, जो कि क्षैतिज समतल पर रखा है, अपने दोलन के न्यूनतम बिन्दु पर प्रत्यास्थ संघट्ट करता है। गोलक संघट्ट कर कोण $θ_{1}$ , तक जाता है, तो M का मान होगा हल देखें
Question 24
एक सरल दोलक का हवा में आवर्तकाल T है। इस दोलक के गोलक को एक श्यानता रहित द्रव, जिसका घनत्व गोलक के घनत्व का $\frac{1}{16}$ है, में दोलन करवाते हैं। यदि दोलन के समय यह गोलक पूर्णतया द्रव में रहता है, तो इसका आवर्तकाल होगा|हल देखें
Question 25
एक अवमन्दित आवर्ती दोलक का विस्थापन निम्न है, $x (t) = e^{- 0.1 t} cos [10 π t + ϕ]$ , यहाँ t सेकण्ड में है। इसके दोलन आयाम को अपने आरम्भिक मान से आधा होने में लगे समय का सन्निकट मान होगा- हल देखें
Question 26
किसी सरल लोलक के लिये, उसके विस्थापन d तथा उसकी गतिज ऊर्जा के बीच और विस्थापन d तथा उसकी स्थितिज ऊर्जा के बीच ग्राफ खींचे गये हैं। निम्नांकित में से कौनसा ग्राफ (आलेख) सही है
(यहाँ ग्राफ केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं)|हल देखें
Question 27
किसी पिण्ड (वस्तु) के चिकने क्षैतिज पृष्ठ (सतह) पर दोलनों के समीकरण को
X = A cos $(ω t)$ द्वारा
निरूपित किया जाता है, जहाँ X = t समय पर विस्थापन
$ω$ = दोलनों की आवृत्ति तो
के साथ a के विचलन (परिवर्तन) को कौनसा ग्राफ (आलेख) सही रूप में दर्शाता है—हल देखें
Question 28
दो स्वतंत्र समान द्रव्यमान के आवर्त दोलन मूल बिन्दु से परितः कोणीय आवृत्तियों $ω_{1}$ , एवं $ω_{2}$ , तथा कुल ऊर्जाओं क्रमश: $E_{1}$ , तथा $E_{2}$ से दोलन कर रहे हैं। उनके संवेगों (p) का स्थिति x के साथ परिवर्तन सम्बन्ध चित्रों में दर्शाये गये हैं। यदि $\frac{a}{b}$ = $n^{2}$ तथा $\frac{a}{R} = n$ है, तब सही कथन है
हल देखें
Question 29
जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = $k x^{2}$ ', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल $\sqrt{\frac{m}{k}}$ के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ $k x^{2}$ से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = $a x^{4}$ , (a>0) है तथा |x|> $X_{0}$ के लिए स्थितिज ऊर्जा V(x) = $V_{0}$ , है (चित्र देखें) .
Q. यदि एक कण की समग्र ऊर्जा E है, तो वह आवर्ती गति करेगा केवल जबकि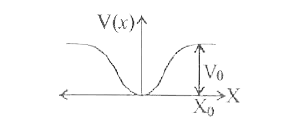
हल देखें
Question 30
जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = $k x^{2}$ ', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल $\sqrt{\frac{m}{k}}$ के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ $k x^{2}$ से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = $a x^{4}$ , (a>0) है तथा |x|> $X_{0}$ के लिए स्थितिज ऊर्जा V(x) = $V_{0}$ , है (चित्र देखें) .
Q. कम आयाम A के दोलन के लिए, कण का आवर्तकाल T निम्न में से किसके समानुपाती है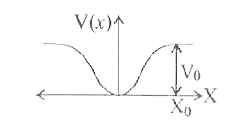
हल देखें
Question 31
जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = $k x^{2}$ ', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल $\sqrt{\frac{m}{k}}$ के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ $k x^{2}$ से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = $a x^{4}$ , (a>0) है तथा |x|> $X_{0}$ के लिए स्थितिज ऊर्जा V(x) = $V_{0}$ , है (चित्र देखें) .
Q |x|> $X_{0}$ के लिए कण का त्वरण-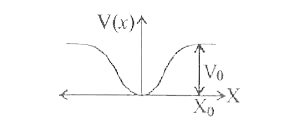
हल देखें

SANJEEV PUBLICATION दोलन की सभी प्रश्नावली कक्षा 11 के लिए

Home
Ask Doubt
Profile