पृष्ठ तनाव कक्षा 11 भौतिकी
भूमिका
इस अध्याय में श्यानता, रेनॉल्ड संख्या, पृष्ठ तनाव तथा केशिकत्व के बारे में जानेंगे। जिसमे अंतराणविक बल के बारे मे जानना भी आवश्यक हैं। जिसका अध्ययन इस अध्याय में करेंगे। साथ ही पृष्ठ तनाव पर आधारित कुछ घटनाएँ तथा प्रभावित करने वाले कारकों के बारे में भी अध्ययन करेंगे। तथा इस से जुड़े अंकिक प्रश्नों का उदाहरण लेकर समस्याओं को हल करने का तरीका सीखेंगे।
भूमिका
इस अध्याय में श्यानता, रेनॉल्ड संख्या, पृष्ठ तनाव तथा केशिकत्व के बारे में जानेंगे। जिसमे अंतराणविक बल के बारे मे जानना भी आवश्यक हैं। जिसका अध्ययन इस अध्याय में करेंगे। साथ ही पृष्ठ तनाव पर आधारित कुछ घटनाएँ तथा प्रभावित करने वाले कारकों के बारे में भी अध्ययन करेंगे। तथा इस से जुड़े अंकिक प्रश्नों का उदाहरण लेकर समस्याओं को हल करने का तरीका सीखेंगे।
अन्तर आण्विक बल
अणुओं के मध्य कार्य करने वाले आकर्षण या प्रतिकर्षण बल को अन्तर आण्विक बल कहते है।
अन्तर आण्विक बलों के प्रकृति वैद्युत चुम्बकीय होती है। अन्तर आण्विक आकर्षण बल दो प्रकार के होते है :-
(1) ससंजक बल : प्रत्येक पदार्थ अणुओं से मिलकर बना होता है जिनके मध्य आकर्षण बल लगता है। एक ही पदार्थ के अणुओं के मध्य लगने वाले आकर्षण बल को ससंजक बल कहते है।
उदाहरण - जल के अणुओं के मध्य लगने वाला बल, पारे के अणुओं के मध्य लगने वाला बल।
(2) आसंजक बल : दो भिन्न प्रकार के अणुओं के मध्य लगने वाले आकर्षण बल को आसंजक बल कहते हैं।
उदाहरण - कागज व स्याही के अणुओं के मध्य लगने वाला बल।
अन्तराणविक बल गुरूत्वाकर्षण बल से भिन्न होता है तथा व्युत्क्रम वर्ग नियम का पालन नहीं करता है।
जिस दूरी तक ये बल प्रभावी होते हैं उसे आणविक परास कहते हैं। यह दूरी लगभग 10−9m होती है। इस सीमा में दूरी के घटने के साथ यह बल तेजी से बढ़ता है।
आणविक परास का मान पदार्थ की प्रकृति पर निर्भर करता है।
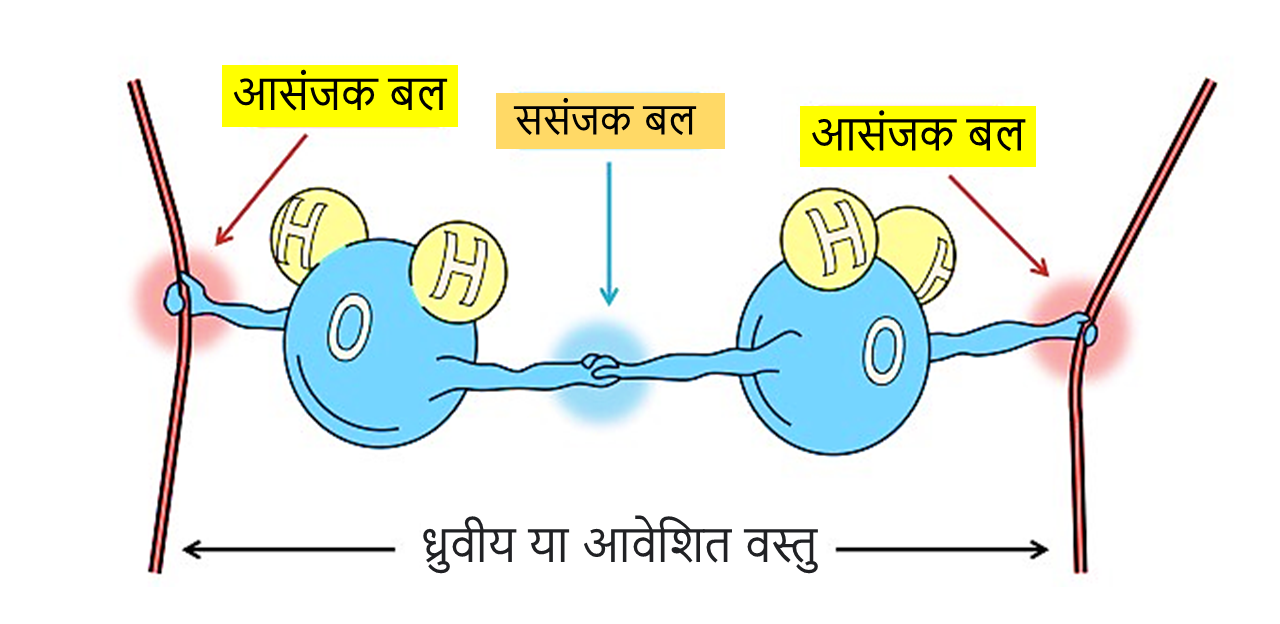
अन्तर आण्विक बल
अणुओं के मध्य कार्य करने वाले आकर्षण या प्रतिकर्षण बल को अन्तर आण्विक बल कहते है।
अन्तर आण्विक बलों के प्रकृति वैद्युत चुम्बकीय होती है। अन्तर आण्विक आकर्षण बल दो प्रकार के होते है :-
(1) ससंजक बल : प्रत्येक पदार्थ अणुओं से मिलकर बना होता है जिनके मध्य आकर्षण बल लगता है। एक ही पदार्थ के अणुओं के मध्य लगने वाले आकर्षण बल को ससंजक बल कहते है।
उदाहरण - जल के अणुओं के मध्य लगने वाला बल, पारे के अणुओं के मध्य लगने वाला बल।
(2) आसंजक बल : दो भिन्न प्रकार के अणुओं के मध्य लगने वाले आकर्षण बल को आसंजक बल कहते हैं।
उदाहरण - कागज व स्याही के अणुओं के मध्य लगने वाला बल।
अन्तराणविक बल गुरूत्वाकर्षण बल से भिन्न होता है तथा व्युत्क्रम वर्ग नियम का पालन नहीं करता है।
जिस दूरी तक ये बल प्रभावी होते हैं उसे आणविक परास कहते हैं। यह दूरी लगभग 10−9m होती है। इस सीमा में दूरी के घटने के साथ यह बल तेजी से बढ़ता है।
आणविक परास का मान पदार्थ की प्रकृति पर निर्भर करता है।

पृष्ठ तनाव
जब काँच की स्वच्छ प्लेट पर थोड़ा-सा जल डाला जाता है, तो जल एक पतली फिल्म के रूप में चारों ओर फैल जाता है। किन्तु पारे की थोड़ी-सी मात्रा को काँच की प्लेट पर डाला जाता है, तो वह गोलाकार बूंद का रूप ले लेता है। इसी प्रकार यदि जल की थोड़ी मात्रा ग्रीस लगी कांच की प्लेट पर डाली जाये, तो वह भी पारे की तरह छोटी-छोटी बूंदों का रूप धारण कर लेता है।
इससे यह निष्कर्ष निकलता है कि द्रवों का व्यवहार केवल गुरुत्वाकर्षण बल (भार) से ही नियन्त्रित नहीं है बल्कि उस पर कोई अन्य बल भी कार्य करता है जो सम्पर्क में आयी सतहों को प्रकृति पर निर्भर करता है। यदि द्रव का भार नगण्य हो, तो उसकी आकृति पूर्ण गोलाकार होगी। उदाहरण के लिये, वर्षा की बूंदे तथा साबुन के बुलबुले पूर्ण गोलाकार होते हैं।

किसी द्रव में उसके अणुओं के मध्य ससंजक बल लगता है जिसके कारण उसका स्वतंत्र पृष्ठ तनी हुई झिल्ली की भाँति कार्य करता है। कोई भी वस्तु जब तनाव अवस्था में होता है तो उसकी यह प्रवृत्ति होती है कि संकुचित होकर तनाव मुक्त हो जाये।
अर्थात् द्रव का स्वतंत्र पृष्ठ तनाव की स्थिति में रहता है तथा उसमें कम से कम क्षेत्रफल प्राप्त करने की प्रवृत्ति होती है। द्रव के पृष्ठ पर लगने वाले इसी तनाव बल को उसका पृष्ठ तनाव कहते हैं।
पृष्ठ तनाव के कारण द्रव अपने पृष्ठ के क्षेत्रफल को न्यूनतम करने का प्रयास करता है। दिये गये आयतन के लिये गोले का पृष्ठीय क्षेत्रफल न्यूनतम होता है। अतः द्रव की छोटी बूँदें गोलीय होती हैं। बूँदों का आकार बढ़ने पर गुरुत्वीय प्रभाव के कारण चपटा होना प्रारंभ हो जाता है।
पृष्ठ तनाव की गणितीय परिभाषा :
माना कि किसी द्रव के पृष्ठ में एक काल्पनिक रेखा AB किसी भी दिशा में खींची गई हैं। इस रेखा के प्रत्येक ओर का पृष्ठ दूसरी ओर वाले पृष्ठ पर कर्षण-बल (pulling force) F लगाता है। यह बल, रेखा AB के लम्बरूप तथा पृष्ठ के तल में स्थित होता है।
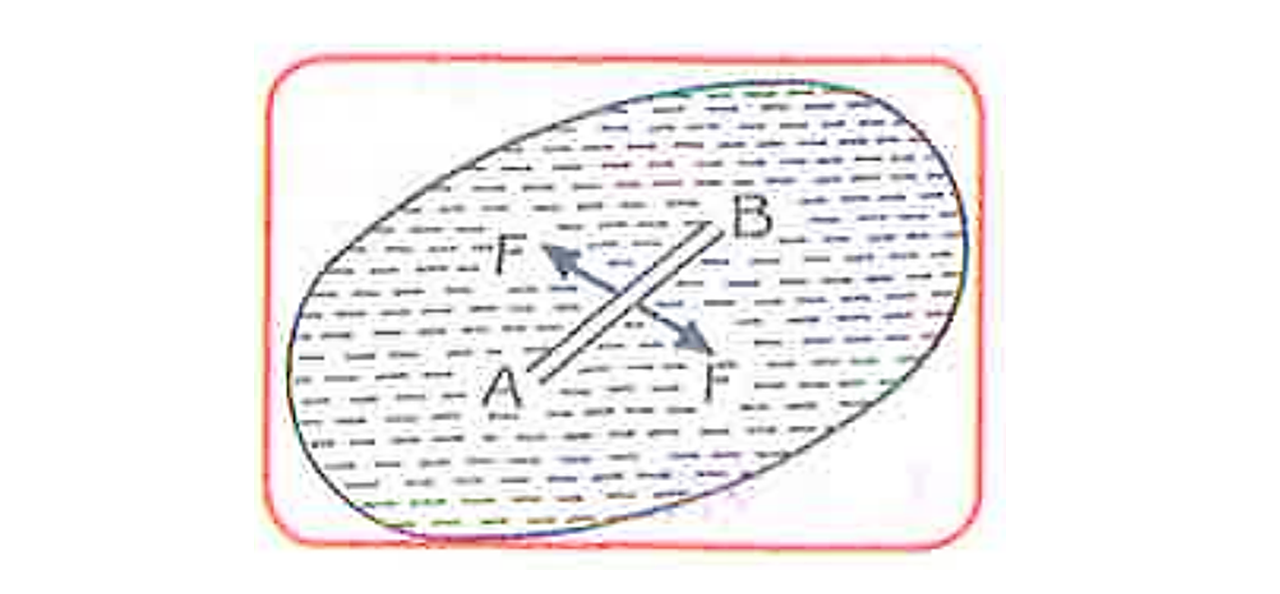
रेखा AB की एकांक लम्बाई पर कार्य करने वाले बल का परिमाण ही द्रव के पृष्ठ-तनाव की माप है। अतः यदि AB की लम्बाई l हो तथा इसके किसी भी ओर कार्य करने वाला सम्पूर्ण बल F हो, तो पृष्ठ- तनाव,
T=Fl
यदि l=1, तो T=F
अतः किसी द्रव का पृष्ठ-तनाव वह बल है जो की द्रव के पृष्ठ पर खींची गई किसी काल्पनिक रेखा की एकांक लम्बाई पर पृष्ठ के तल में तथा रेखा के लंबरूप कार्य करता है।
इसका S.I. मात्रक 'न्यूटन/मीटर' तथा विमा [MT−2] है।
किसी द्रव के लिये पृष्ठ-तनाव का मान द्रव की प्रकृति, द्रव के ताप तथा उस माध्यम पर निर्भर करता है जो द्रव के पृष्ठ के दूसरी ओर होता है। द्रव का ताप बढ़ने पर द्रव का पृष्ठ-तनाव घटता है। द्रव के क्रान्तिक ताप पर पृष्ठ-तनाव शून्य होता है।
पृष्ठ तनाव के कुछ प्रमाण :
ग्रीस लगी हुई सुई को ब्लाटिंग पेपर पर रखकर पानी में तैराने पर कुछ समय बाद ब्लाटिंग पेपर पानी में डूब जाता है परन्तु सुई पानी की सतह पर तैरती रहती है। इस स्थिति में पानी का पृष्ठ तनाव सुई के भार को संतुलित करता है।

पृष्ठ तनाव
जब काँच की स्वच्छ प्लेट पर थोड़ा-सा जल डाला जाता है, तो जल एक पतली फिल्म के रूप में चारों ओर फैल जाता है। किन्तु पारे की थोड़ी-सी मात्रा को काँच की प्लेट पर डाला जाता है, तो वह गोलाकार बूंद का रूप ले लेता है। इसी प्रकार यदि जल की थोड़ी मात्रा ग्रीस लगी कांच की प्लेट पर डाली जाये, तो वह भी पारे की तरह छोटी-छोटी बूंदों का रूप धारण कर लेता है।
इससे यह निष्कर्ष निकलता है कि द्रवों का व्यवहार केवल गुरुत्वाकर्षण बल (भार) से ही नियन्त्रित नहीं है बल्कि उस पर कोई अन्य बल भी कार्य करता है जो सम्पर्क में आयी सतहों को प्रकृति पर निर्भर करता है। यदि द्रव का भार नगण्य हो, तो उसकी आकृति पूर्ण गोलाकार होगी। उदाहरण के लिये, वर्षा की बूंदे तथा साबुन के बुलबुले पूर्ण गोलाकार होते हैं।

किसी द्रव में उसके अणुओं के मध्य ससंजक बल लगता है जिसके कारण उसका स्वतंत्र पृष्ठ तनी हुई झिल्ली की भाँति कार्य करता है। कोई भी वस्तु जब तनाव अवस्था में होता है तो उसकी यह प्रवृत्ति होती है कि संकुचित होकर तनाव मुक्त हो जाये।
अर्थात् द्रव का स्वतंत्र पृष्ठ तनाव की स्थिति में रहता है तथा उसमें कम से कम क्षेत्रफल प्राप्त करने की प्रवृत्ति होती है। द्रव के पृष्ठ पर लगने वाले इसी तनाव बल को उसका पृष्ठ तनाव कहते हैं।
पृष्ठ तनाव के कारण द्रव अपने पृष्ठ के क्षेत्रफल को न्यूनतम करने का प्रयास करता है। दिये गये आयतन के लिये गोले का पृष्ठीय क्षेत्रफल न्यूनतम होता है। अतः द्रव की छोटी बूँदें गोलीय होती हैं। बूँदों का आकार बढ़ने पर गुरुत्वीय प्रभाव के कारण चपटा होना प्रारंभ हो जाता है।
पृष्ठ तनाव की गणितीय परिभाषा :
माना कि किसी द्रव के पृष्ठ में एक काल्पनिक रेखा AB किसी भी दिशा में खींची गई हैं। इस रेखा के प्रत्येक ओर का पृष्ठ दूसरी ओर वाले पृष्ठ पर कर्षण-बल (pulling force) F लगाता है। यह बल, रेखा AB के लम्बरूप तथा पृष्ठ के तल में स्थित होता है।

रेखा AB की एकांक लम्बाई पर कार्य करने वाले बल का परिमाण ही द्रव के पृष्ठ-तनाव की माप है। अतः यदि AB की लम्बाई l हो तथा इसके किसी भी ओर कार्य करने वाला सम्पूर्ण बल F हो, तो पृष्ठ- तनाव,
T=Fl
यदि l=1, तो T=F
अतः किसी द्रव का पृष्ठ-तनाव वह बल है जो की द्रव के पृष्ठ पर खींची गई किसी काल्पनिक रेखा की एकांक लम्बाई पर पृष्ठ के तल में तथा रेखा के लंबरूप कार्य करता है।
इसका S.I. मात्रक 'न्यूटन/मीटर' तथा विमा [MT−2] है।
किसी द्रव के लिये पृष्ठ-तनाव का मान द्रव की प्रकृति, द्रव के ताप तथा उस माध्यम पर निर्भर करता है जो द्रव के पृष्ठ के दूसरी ओर होता है। द्रव का ताप बढ़ने पर द्रव का पृष्ठ-तनाव घटता है। द्रव के क्रान्तिक ताप पर पृष्ठ-तनाव शून्य होता है।
पृष्ठ तनाव के कुछ प्रमाण :
ग्रीस लगी हुई सुई को ब्लाटिंग पेपर पर रखकर पानी में तैराने पर कुछ समय बाद ब्लाटिंग पेपर पानी में डूब जाता है परन्तु सुई पानी की सतह पर तैरती रहती है। इस स्थिति में पानी का पृष्ठ तनाव सुई के भार को संतुलित करता है।

पृष्ठ तनाव का आण्विक सिद्धान्त
लॉप्लास नामक वैज्ञानिक ने आण्विक सिद्धान्त के आधार पर पृष्ठ तनाव की घटना की व्याख्या की। "जिसके किन्हीं दो अणुओं के बीच लगने वाला ससंजक बल उनके बीच की दूरी बढ़ने पर तेजी से घटता है। वह अधिकतम दूरी जहाँ तक अणुओं के मध्य ससंजक बल लगता है उसे आण्विक परास कहते हैं।"
अलग-अलग पदार्थों के लिये आण्विक परास का मान अलग-अलग होता है, परन्तु यह 10−7 सेमी कोटि का होता है। अतः यदि किसी अणु को केन्द्र मानकर आण्विक परास के बराबर त्रिज्या का एक गोला खींचें तो इस गोले के अन्दर जितने अणु आयेंगे उन अणुओं द्वारा केन्द्र पर आकर्षण बल लगेगा। इसके बाहर के अणुओं का केन्द्रीय अणु पर कोई प्रभाव नहीं पड़ता। इस गोले को आण्विक प्रभाव का गोला कहते हैं।
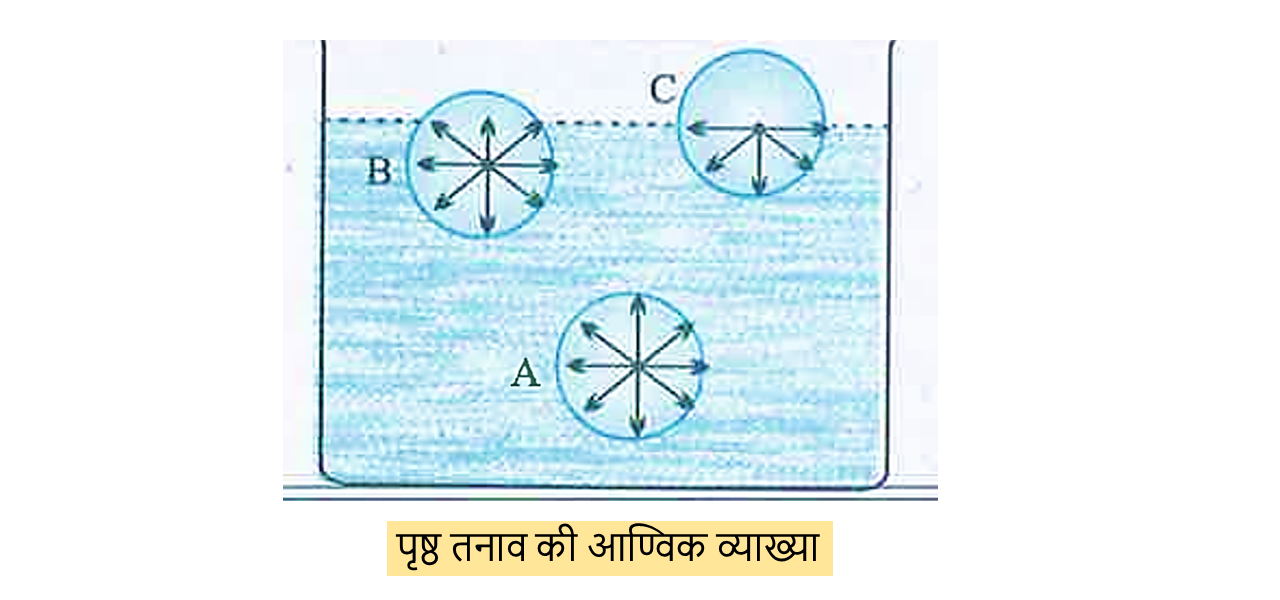
इस विश्लेषण से यह स्पष्ट है कि द्रव के पृष्ठ पर स्थित प्रत्येक अणु पर नीचे की ओर अधिकतम आकर्षण बल लगता है। पृष्ठ से नीचे की ओर जाने पर इसका मान क्रमशः कम होता जाता है। द्रव के स्वतंत्र सतह से आण्विक परास तक जाने पर यह बल शून्य हो जाता है। द्रव के स्वतंत्र सतह से आण्विक परास की गहराई तक द्रव का भाग पृष्ठीय फिल्म कहलाता है। पृष्ठीय फिल्म के सभी अणु पर नीचे की दिशा में परिणामी आकर्षण बल लगता है।
पृष्ठ तनाव का आण्विक सिद्धान्त
लॉप्लास नामक वैज्ञानिक ने आण्विक सिद्धान्त के आधार पर पृष्ठ तनाव की घटना की व्याख्या की। "जिसके किन्हीं दो अणुओं के बीच लगने वाला ससंजक बल उनके बीच की दूरी बढ़ने पर तेजी से घटता है। वह अधिकतम दूरी जहाँ तक अणुओं के मध्य ससंजक बल लगता है उसे आण्विक परास कहते हैं।"
अलग-अलग पदार्थों के लिये आण्विक परास का मान अलग-अलग होता है, परन्तु यह 10−7 सेमी कोटि का होता है। अतः यदि किसी अणु को केन्द्र मानकर आण्विक परास के बराबर त्रिज्या का एक गोला खींचें तो इस गोले के अन्दर जितने अणु आयेंगे उन अणुओं द्वारा केन्द्र पर आकर्षण बल लगेगा। इसके बाहर के अणुओं का केन्द्रीय अणु पर कोई प्रभाव नहीं पड़ता। इस गोले को आण्विक प्रभाव का गोला कहते हैं।

इस विश्लेषण से यह स्पष्ट है कि द्रव के पृष्ठ पर स्थित प्रत्येक अणु पर नीचे की ओर अधिकतम आकर्षण बल लगता है। पृष्ठ से नीचे की ओर जाने पर इसका मान क्रमशः कम होता जाता है। द्रव के स्वतंत्र सतह से आण्विक परास तक जाने पर यह बल शून्य हो जाता है। द्रव के स्वतंत्र सतह से आण्विक परास की गहराई तक द्रव का भाग पृष्ठीय फिल्म कहलाता है। पृष्ठीय फिल्म के सभी अणु पर नीचे की दिशा में परिणामी आकर्षण बल लगता है।
पृष्ठ तनाव को प्रभावित करने वाले कारक
अलग-अलग द्रवों के पृष्ठ तनाव अलग-अलग होते है। किसी द्रव का पृष्ठ तनाव नियत होता है, परन्तु वातावरण परिवर्तित होने पर उसका मान भी परिवर्तित हो जाता है। द्रव के पृष्ठ तनाव को प्रभावित करने वाले कारक तथा प्रभाव निम्न है :-
द्रव में विलेय पदार्थ :
यदि द्रव में विलेय पदार्थ अत्यधिक घुलनशील हो, तो द्रव का पृष्ठ तनाव बढ़ जाता है। उदाहरण - पानी में नमक या शक्कर घोलने पर उसका पृष्ठ तनाव बढ़ जाता है। किन्तु यदि विलेय पदार्थ कम घुलनशील हो, तो पृष्ठ तनाव का मान कम हो जाता है। उदाहरण - पानी में साबुन या फिनाइल डालने पर उसका पृष्ठ तनाव कम हो जाता है।
द्रव के पृष्ठ पर प्रदूषण :
यदि द्रव के पृष्ठ पर धूल के कण या कोई चिकनाई (तेल या ग्रीस) विद्यमान है, तो द्रव का पृष्ठ तनाव कम हो जाता है।
द्रव का ताप :
प्रायः ताप बढ़ाने पर द्रवों का पृष्ठ तनाव कम हो जाता है, क्योंकि ताप में वृद्धि करने से ससंजक बल का मान कम हो जाता है।
यदि 0°C पर द्रव का पृष्ठ तनाव To,t∘C पर पृष्ठ तनाव T हो और पृष्ठ तनाव के लिये ताप गुणांक α हो, तो
T=To(1−αt) ... (1)
इस सूत्र की सहायता से अलग-अलग ताप पर किसी द्रव का पृष्ठ तनाव ज्ञात किया जा सकता है।
द्रव का विद्युतीकरण :
द्रव के विद्युतीकरण से उसका पृष्ठतनाव कम हो जाता है क्योंकि इसके कारण द्रव के स्वतंत्र पृष्ठ के लम्बवत् बाहर की दिशा में एक बल लगता है।
पृष्ठ तनाव को प्रभावित करने वाले कारक
अलग-अलग द्रवों के पृष्ठ तनाव अलग-अलग होते है। किसी द्रव का पृष्ठ तनाव नियत होता है, परन्तु वातावरण परिवर्तित होने पर उसका मान भी परिवर्तित हो जाता है। द्रव के पृष्ठ तनाव को प्रभावित करने वाले कारक तथा प्रभाव निम्न है :-
द्रव में विलेय पदार्थ :
यदि द्रव में विलेय पदार्थ अत्यधिक घुलनशील हो, तो द्रव का पृष्ठ तनाव बढ़ जाता है। उदाहरण - पानी में नमक या शक्कर घोलने पर उसका पृष्ठ तनाव बढ़ जाता है। किन्तु यदि विलेय पदार्थ कम घुलनशील हो, तो पृष्ठ तनाव का मान कम हो जाता है। उदाहरण - पानी में साबुन या फिनाइल डालने पर उसका पृष्ठ तनाव कम हो जाता है।

द्रव के पृष्ठ पर प्रदूषण :
यदि द्रव के पृष्ठ पर धूल के कण या कोई चिकनाई (तेल या ग्रीस) विद्यमान है, तो द्रव का पृष्ठ तनाव कम हो जाता है।
द्रव का ताप :
प्रायः ताप बढ़ाने पर द्रवों का पृष्ठ तनाव कम हो जाता है, क्योंकि ताप में वृद्धि करने से ससंजक बल का मान कम हो जाता है।
यदि 0°C पर द्रव का पृष्ठ तनाव To,t∘C पर पृष्ठ तनाव T हो और पृष्ठ तनाव के लिये ताप गुणांक α हो, तो
T=To(1−αt) ... (1)
इस सूत्र की सहायता से अलग-अलग ताप पर किसी द्रव का पृष्ठ तनाव ज्ञात किया जा सकता है।
द्रव का विद्युतीकरण :
द्रव के विद्युतीकरण से उसका पृष्ठतनाव कम हो जाता है क्योंकि इसके कारण द्रव के स्वतंत्र पृष्ठ के लम्बवत् बाहर की दिशा में एक बल लगता है।
पृष्ठ तनाव पर आधारित कुछ घटनायें
- काँच की नली के सिरों का बर्नर की ज्वाला में गर्म होने पर गोल हो जाना।
- पारें की छोटी बूँदें गोल तथा बड़ी बूँदें चपटी होती है।

- सीसे के छर्रे बनाना।
- फ़ुहारने से ठंडक उत्पन्न होती है।
- सुई का जल पर तैरना।
- जल के पृष्ठ पर कपूर के टुकड़ो का नाचना।
- साधारण जल की अपेक्षा साबुन के घोल के अधिक बड़े बुलबुले बनाए जा सकते है।
- साबुन मिला हुआ जल शुद्ध जल की अपेक्षा कपड़ों की अधिक सफाई करता है।

पृष्ठ तनाव के अनुप्रयोग :
- घाव धोने के लिए डिटाल या स्प्रिट का उपयोग करते है।
- छोटे-छोटे गड्ढ़ों में मच्छर मारने के लिए मिट्टी का तेल डालते है। जिससे पृष्ठ तनाव कम हो जाता है और मच्छर पानी में डूब के मर जाते है।
- टूथपेस्ट के झागों का पृष्ठ तनाव कम होता है। अतः वह दाँतो के अधिक क्षेत्रफल में फैलकर दाँतो की सफाई कर देता है।
- सीसे के गोल छर्रे बनाने के लिये सीसे को पिघलाकर ऊँचाई से फुहार के रूप में पानी गिराते है।
- ठंडे पानी की अपेक्षा गर्म पानी से कपड़े ज्यादा साफ होते है। पानी को गर्म करने पर उसका पृष्ठ तनाव कम हो जाता है। अतः गर्म पानी ठंडे पानी अपेक्षा अधिक क्षेत्रफल में फैलकर गंदगी के कणों को हटा देता है।
- यदि स्याही सोखता पर एक सुई रखकर उसे पानी की सतह पर रख दिया जाये, तो कुछ देर पश्यात् स्याही सोखता पानी में डूब जाता है, किन्तु सुई तैरने लगती है।
- पृष्ठ तनाव के कारण कीड़े पानी पर आसानी से चलते है।
पृष्ठ तनाव पर आधारित कुछ घटनायें
- काँच की नली के सिरों का बर्नर की ज्वाला में गर्म होने पर गोल हो जाना।
- पारें की छोटी बूँदें गोल तथा बड़ी बूँदें चपटी होती है।

- सीसे के छर्रे बनाना।
- फ़ुहारने से ठंडक उत्पन्न होती है।
- सुई का जल पर तैरना।
- जल के पृष्ठ पर कपूर के टुकड़ो का नाचना।
- साधारण जल की अपेक्षा साबुन के घोल के अधिक बड़े बुलबुले बनाए जा सकते है।
- साबुन मिला हुआ जल शुद्ध जल की अपेक्षा कपड़ों की अधिक सफाई करता है।

पृष्ठ तनाव के अनुप्रयोग :
- घाव धोने के लिए डिटाल या स्प्रिट का उपयोग करते है।
- छोटे-छोटे गड्ढ़ों में मच्छर मारने के लिए मिट्टी का तेल डालते है। जिससे पृष्ठ तनाव कम हो जाता है और मच्छर पानी में डूब के मर जाते है।
- टूथपेस्ट के झागों का पृष्ठ तनाव कम होता है। अतः वह दाँतो के अधिक क्षेत्रफल में फैलकर दाँतो की सफाई कर देता है।
- सीसे के गोल छर्रे बनाने के लिये सीसे को पिघलाकर ऊँचाई से फुहार के रूप में पानी गिराते है।
- ठंडे पानी की अपेक्षा गर्म पानी से कपड़े ज्यादा साफ होते है। पानी को गर्म करने पर उसका पृष्ठ तनाव कम हो जाता है। अतः गर्म पानी ठंडे पानी अपेक्षा अधिक क्षेत्रफल में फैलकर गंदगी के कणों को हटा देता है।
- यदि स्याही सोखता पर एक सुई रखकर उसे पानी की सतह पर रख दिया जाये, तो कुछ देर पश्यात् स्याही सोखता पानी में डूब जाता है, किन्तु सुई तैरने लगती है।
- पृष्ठ तनाव के कारण कीड़े पानी पर आसानी से चलते है।
पृष्ठ ऊर्जा
प्रत्येक द्रव का स्वतंत्र पृष्ठ एक तनी हुई झिल्ली की भाँति व्यवहार करता है, क्योंकि पृष्ठ के अणुओं पर तल के लम्बवत् अंदर की दिशा में परिणामी ससंजक बल कार्य करता है। अतः द्रव के अंदर से किसी अणु को पृष्ठ पर लाने के लिये इस ससंजक बल के विरुद्ध कुछ कार्य करना पड़ता है। यह कार्य द्रव के पृष्ठ पर स्थितिज ऊर्जा के रूप में संचित हो जाता है। द्रव के पृष्ठ पर एकांक क्षेत्रफल की संचित स्थितिज ऊर्जा को द्रव की पृष्ठ ऊर्जा कहते हैं। अलग-अलग द्रवों के लिये पृष्ठ ऊर्जा का मान अलग-अलग होता है।
पृष्ठ ऊर्जा और पृष्ठ तनाव में संबंध :
किसी द्रव की पृष्ठ ऊर्जा तथा पृष्ठ तनाव में संबंध ज्ञात करने के लिये चित्र के अनुसार ABCD तार का एक फ्रेम लेते हैं, जिसमें दूसरा तार PQ फ्रेम की भुजाओं AB तथा DC पर ऊपर-नीचे गति कर सकता है। अब फ्रेम को साबुन के घोल में डुबाकर बाहर निकालने से फ्रेम के PBCQ भाग में एक फिल्म बन जाती है तथा पृष्ठ तनाव के कारण तार PQ पर लगने वाले बल के कारण यह BC की ओर सरकने लगेगा।
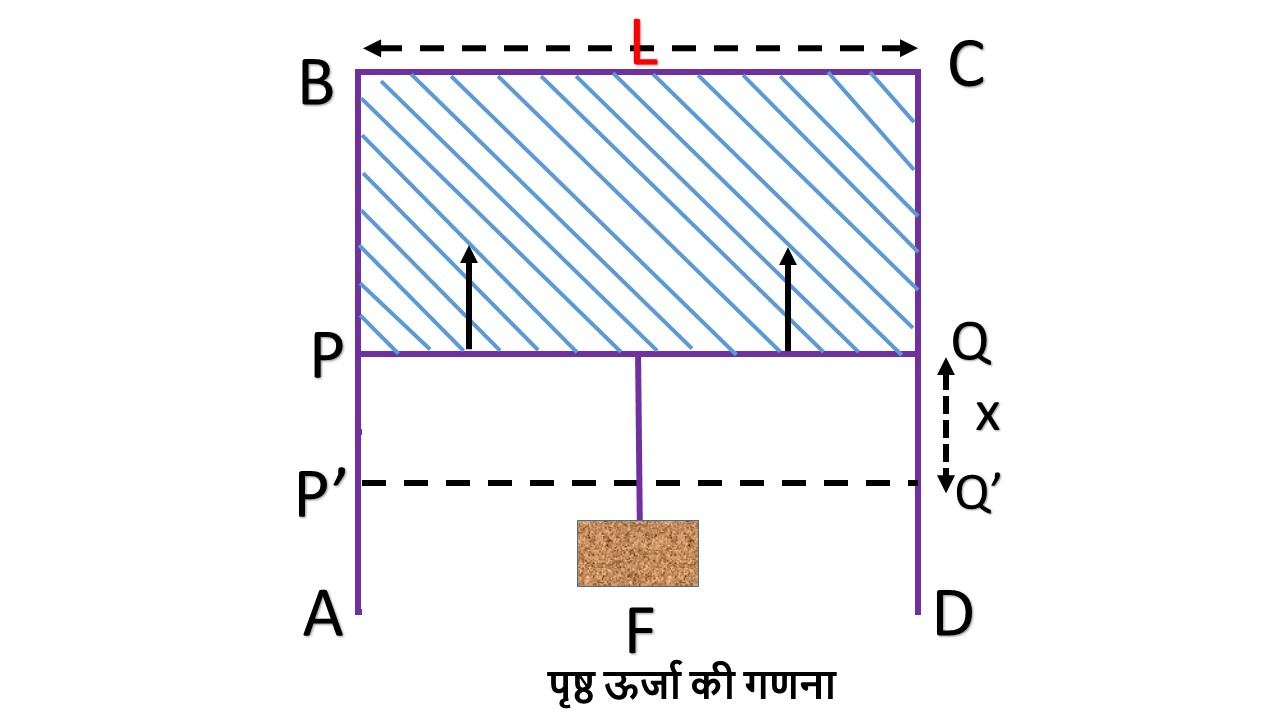
इसे सरकने से रोकने के लिये PQ पर नीचे की दिशा में बल F लगाया जाता है, जिसका परिमाण पृष्ठ तनाव के कारण तार PQ पर ऊपर की दिशा में लगने वाले बल के परिमाण के तुल्य होता है।
यदि साबुन के घोल का पृष्ठ तनाव T तथा तार PQ की लम्बाई L हो, तो पृष्ठ तनाव के कारण तार पर ऊपर की दिशा में लगने वाला बल T.2L होगा, क्योंकि फिल्म में दो स्वतंत्र पृष्ठ हैं, अतः लम्बाई 2L ली गई हैं यह बल F द्वारा संतुलित होता है। अतः
F=T.2L=2TL .....(1)
अब यदि तार PQ को पृष्ठ तनाव के विरुद्ध x दूरी तक विस्थापित किया जाये तो उसकी स्थिति P'Q' हो जाती है। इस विस्थापन में किया गया कार्य
W= बल × विस्थापन
W=Fx
W=2TL.x
W=T.2Lx ....(2)
अब यदि फिल्म के पृष्ठीय क्षेत्रफल में कुल वृद्धि ΔA हो, तो
ΔA=Lx+L.x, (दो पृष्ठों के कारण)
ΔA=2Lx ....(3)
अतः समीकरण (2) और (3) से,
W=T.ΔA ....(4)
यहाँ ΔA फिल्म के क्षेत्रफल में वृद्धि है। यही कार्य का सूत्र है। चूँकि क्षेत्रफल में वृद्धि करने के लिये आवश्यक कार्य उसके स्थितिज ऊर्जा के रूप में संचित होती है। अतः पृष्ठ की स्थितिज ऊर्जा में परिवर्तन उसके पृष्ठ तनाव तथा क्षेत्रफल में परिवर्तन के गुणनफल के तुल्य होता है।
अब समीकरण (4) से,
WΔA=T ....(5)
यही द्रव की पृष्ठ ऊर्जा का सूत्र है, जिससे यह स्पष्ट होता है कि द्रव की पृष्ठ ऊर्जा उसके पृष्ठ तनाव के तुल्य होती है। समीकरण (5) में यदि ΔA=1 हो, तो
T=W
अर्थात् किसी द्रव के स्वतंत्र पृष्ठ के क्षेत्रफल में एकांक वृद्धि करने के लिये आवश्यक कार्य को द्रव का पृष्ठ तनाव कहते हैं।
पृष्ठ ऊर्जा
प्रत्येक द्रव का स्वतंत्र पृष्ठ एक तनी हुई झिल्ली की भाँति व्यवहार करता है, क्योंकि पृष्ठ के अणुओं पर तल के लम्बवत् अंदर की दिशा में परिणामी ससंजक बल कार्य करता है। अतः द्रव के अंदर से किसी अणु को पृष्ठ पर लाने के लिये इस ससंजक बल के विरुद्ध कुछ कार्य करना पड़ता है। यह कार्य द्रव के पृष्ठ पर स्थितिज ऊर्जा के रूप में संचित हो जाता है। द्रव के पृष्ठ पर एकांक क्षेत्रफल की संचित स्थितिज ऊर्जा को द्रव की पृष्ठ ऊर्जा कहते हैं। अलग-अलग द्रवों के लिये पृष्ठ ऊर्जा का मान अलग-अलग होता है।
पृष्ठ ऊर्जा और पृष्ठ तनाव में संबंध :
किसी द्रव की पृष्ठ ऊर्जा तथा पृष्ठ तनाव में संबंध ज्ञात करने के लिये चित्र के अनुसार ABCD तार का एक फ्रेम लेते हैं, जिसमें दूसरा तार PQ फ्रेम की भुजाओं AB तथा DC पर ऊपर-नीचे गति कर सकता है। अब फ्रेम को साबुन के घोल में डुबाकर बाहर निकालने से फ्रेम के PBCQ भाग में एक फिल्म बन जाती है तथा पृष्ठ तनाव के कारण तार PQ पर लगने वाले बल के कारण यह BC की ओर सरकने लगेगा।

इसे सरकने से रोकने के लिये PQ पर नीचे की दिशा में बल F लगाया जाता है, जिसका परिमाण पृष्ठ तनाव के कारण तार PQ पर ऊपर की दिशा में लगने वाले बल के परिमाण के तुल्य होता है।
यदि साबुन के घोल का पृष्ठ तनाव T तथा तार PQ की लम्बाई L हो, तो पृष्ठ तनाव के कारण तार पर ऊपर की दिशा में लगने वाला बल T.2L होगा, क्योंकि फिल्म में दो स्वतंत्र पृष्ठ हैं, अतः लम्बाई 2L ली गई हैं यह बल F द्वारा संतुलित होता है। अतः
F=T.2L=2TL .....(1)
अब यदि तार PQ को पृष्ठ तनाव के विरुद्ध x दूरी तक विस्थापित किया जाये तो उसकी स्थिति P'Q' हो जाती है। इस विस्थापन में किया गया कार्य
W= बल × विस्थापन
W=Fx
W=2TL.x
W=T.2Lx ....(2)
अब यदि फिल्म के पृष्ठीय क्षेत्रफल में कुल वृद्धि ΔA हो, तो
ΔA=Lx+L.x, (दो पृष्ठों के कारण)
ΔA=2Lx ....(3)
अतः समीकरण (2) और (3) से,
W=T.ΔA ....(4)
यहाँ ΔA फिल्म के क्षेत्रफल में वृद्धि है। यही कार्य का सूत्र है। चूँकि क्षेत्रफल में वृद्धि करने के लिये आवश्यक कार्य उसके स्थितिज ऊर्जा के रूप में संचित होती है। अतः पृष्ठ की स्थितिज ऊर्जा में परिवर्तन उसके पृष्ठ तनाव तथा क्षेत्रफल में परिवर्तन के गुणनफल के तुल्य होता है।
अब समीकरण (4) से,
WΔA=T ....(5)
यही द्रव की पृष्ठ ऊर्जा का सूत्र है, जिससे यह स्पष्ट होता है कि द्रव की पृष्ठ ऊर्जा उसके पृष्ठ तनाव के तुल्य होती है। समीकरण (5) में यदि ΔA=1 हो, तो
T=W
अर्थात् किसी द्रव के स्वतंत्र पृष्ठ के क्षेत्रफल में एकांक वृद्धि करने के लिये आवश्यक कार्य को द्रव का पृष्ठ तनाव कहते हैं।
उदाहरण 1
एक 2.5 cm लम्बाई की सुई पानी पर तैर रही है। सुई को पानी से बाहर खिचने के लिए आवश्यक अतिरिक्त बल का मान ज्ञात करो [T=7.2×10−2N/m]
पृष्ठ तनाव के कारण बल F=T×2l
F=7.2×10−2×2×2.5×10−2
=3.6×10−3N ( ∴ यहाँ पर दो मुक्त सतह उपस्थित है।)
उदाहरण 1
एक 2.5 cm लम्बाई की सुई पानी पर तैर रही है। सुई को पानी से बाहर खिचने के लिए आवश्यक अतिरिक्त बल का मान ज्ञात करो [T=7.2×10−2N/m]
पृष्ठ तनाव के कारण बल F=T×2l
F=7.2×10−2×2×2.5×10−2
=3.6×10−3N ( ∴ यहाँ पर दो मुक्त सतह उपस्थित है।)
उदाहरण 2
एक R त्रिज्या की कागज की चकती में r त्रिज्या का एक छिद्र काट कर T पृष्ठ तनाव के द्रव में तैराया जाता है। पृष्ठ तनाव के कारण चकती पर बल कितना होगा?
T=FL=F2π(R+r)
∴F=2π(R+r)T
उदाहरण 2
एक R त्रिज्या की कागज की चकती में r त्रिज्या का एक छिद्र काट कर T पृष्ठ तनाव के द्रव में तैराया जाता है। पृष्ठ तनाव के कारण चकती पर बल कितना होगा?
T=FL=F2π(R+r)
∴F=2π(R+r)T
उदाहरण 3
चित्र में दर्शाये अनुसार PQRS तांबे के तार का एक आयताकार फ्रेम है जिसकी भुजा RS चल सकती है। यदि इसमें एक साबुन की झिल्ली बना दी जाये तो साम्यावस्था के लिए तार का व्यास क्या होगा? साबुन के घोल का पृष्ठ तनाव = 0.045 N/m तथा तांबे का घनत्व= 8.96×103kg/m3
पृष्ठ तनाव के कारण बल - तार का भार
⇒2Tl=mg=πr2ldg
⇒r=√2Tπdg
⇒r=√2×0.0453.14×8.96×103×9.8=0.57mm,
अत: व्यास =2×0.57=1.14mm
उदाहरण 3
चित्र में दर्शाये अनुसार PQRS तांबे के तार का एक आयताकार फ्रेम है जिसकी भुजा RS चल सकती है। यदि इसमें एक साबुन की झिल्ली बना दी जाये तो साम्यावस्था के लिए तार का व्यास क्या होगा? साबुन के घोल का पृष्ठ तनाव = 0.045 N/m तथा तांबे का घनत्व= 8.96×103kg/m3
पृष्ठ तनाव के कारण बल - तार का भार
⇒2Tl=mg=πr2ldg
⇒r=√2Tπdg
⇒r=√2×0.0453.14×8.96×103×9.8=0.57mm,
अत: व्यास =2×0.57=1.14mm
उदाहरण 4
एक ही समान पदार्थ से बनी एक दृढ़ वलय तथा एक दृढ़ पतली चकती B को जब पानी की सतह पर धीरे से रखते हैं तो वे चित्रानुसार पृष्ठतनाव के कारण तैरती है। वलय तथा चकती दोनों की त्रिज्या समान है। उनके द्रव्यमानों के बारे में आप क्या निष्कर्ष निकाल सकते हैं?
वलय में चकती की तुलना में दो सतह होती है अत: वलय का द्रव्यमान चकती के द्रव्यमान की तुलना में दुगना होगा।
उदाहरण 4
एक ही समान पदार्थ से बनी एक दृढ़ वलय तथा एक दृढ़ पतली चकती B को जब पानी की सतह पर धीरे से रखते हैं तो वे चित्रानुसार पृष्ठतनाव के कारण तैरती है। वलय तथा चकती दोनों की त्रिज्या समान है। उनके द्रव्यमानों के बारे में आप क्या निष्कर्ष निकाल सकते हैं?
वलय में चकती की तुलना में दो सतह होती है अत: वलय का द्रव्यमान चकती के द्रव्यमान की तुलना में दुगना होगा।
उदाहरण 5
दो समान्तर तार जिसकी लम्बाई 10 सेमी. है (0.5 सेमी. दूरी पर हैं उनके बीच में एक पानी की फिल्म बनती है। तारों के बीच की दूरी 1 मिमी. बढ़ाने में किये गये कार्य का मान होगा :- (पानी का पृष्ठ तनाव 72 डाइन/सेमी.)
W=T×ΔA
=72×[2×(10×0.6−10×0.5)]=144 अर्ग
उदाहरण 5
दो समान्तर तार जिसकी लम्बाई 10 सेमी. है (0.5 सेमी. दूरी पर हैं उनके बीच में एक पानी की फिल्म बनती है। तारों के बीच की दूरी 1 मिमी. बढ़ाने में किये गये कार्य का मान होगा :- (पानी का पृष्ठ तनाव 72 डाइन/सेमी.)
W=T×ΔA
=72×[2×(10×0.6−10×0.5)]=144 अर्ग
उदाहरण 6
एक साबुन के बुलबुले को 10 cm त्रिज्या से 20 cm त्रिज्या तक फुलाने के लिए पृष्ठ तनाव के विरुद्ध किये गये कार्य को ज्ञात करो यदि साबुन के विलयन का पृष्ठ तनाव 25×10−3N/m है
साबुन के बुलबुले के लिए :
क्षेत्रफल में विस्तार =2×4πr22−2×4πr21
=8π[(0.2)2−(0.1)2]=0.24πm2
अत: किया गया कार्य
W1= पृष्ठ तनाव × विस्तारित क्षेत्रफल
=25×10−3×0.24π
=6π×10−3J
(ii) द्रव बूँद के लिए : द्रव बूँद के लिए केवल एक मुक्त पृष्ठ होता है। अत: इस स्थिति में विस्तारित क्षेत्रफल साबुन के बुलबुले से आधा होगा।
∴W2=W12=3π×10−3J
समान त्रिज्या की स्थिति में द्रव की बूँद के द्वारा किया गया कार्य साबुन के बुलबुले की तुलना में आधा होता है।
उदाहरण 6
एक साबुन के बुलबुले को 10 cm त्रिज्या से 20 cm त्रिज्या तक फुलाने के लिए पृष्ठ तनाव के विरुद्ध किये गये कार्य को ज्ञात करो यदि साबुन के विलयन का पृष्ठ तनाव 25×10−3N/m है
साबुन के बुलबुले के लिए :
क्षेत्रफल में विस्तार =2×4πr22−2×4πr21
=8π[(0.2)2−(0.1)2]=0.24πm2
अत: किया गया कार्य
W1= पृष्ठ तनाव × विस्तारित क्षेत्रफल
=25×10−3×0.24π
=6π×10−3J
(ii) द्रव बूँद के लिए : द्रव बूँद के लिए केवल एक मुक्त पृष्ठ होता है। अत: इस स्थिति में विस्तारित क्षेत्रफल साबुन के बुलबुले से आधा होगा।
∴W2=W12=3π×10−3J
समान त्रिज्या की स्थिति में द्रव की बूँद के द्वारा किया गया कार्य साबुन के बुलबुले की तुलना में आधा होता है।
उदाहरण 7
यदि किसी साबुन के घोल से V आयतन का बुलबुला बनाने में कार्य करना पड़ता हो तो उसी घोल से 2V आयतन का बुलबुला बनाने में किये गये कार्य का मान होगा।
बुलबुले का आयतन V=43πr3⇒V∝r3
2VV=(r2r1)3⇒r2r1=21/3
बुलबुला बनाने में किया गया कार्य
W=8πr2T⇒W∝r2
W2W1=(r2r1)2=(21/3)2=22/3
W2=22/3W1
उदाहरण 7
यदि किसी साबुन के घोल से V आयतन का बुलबुला बनाने में कार्य करना पड़ता हो तो उसी घोल से 2V आयतन का बुलबुला बनाने में किये गये कार्य का मान होगा।
बुलबुले का आयतन V=43πr3⇒V∝r3
2VV=(r2r1)3⇒r2r1=21/3
बुलबुला बनाने में किया गया कार्य
W=8πr2T⇒W∝r2
W2W1=(r2r1)2=(21/3)2=22/3
W2=22/3W1
उदाहरण 8
पानी की 1000 छोटी बूंदों को मिलाकर एक बड़ी बूँद बनायी जाती है। पृष्ठीय ऊर्जा में क्या परिवर्तन होगा। छोटी बूंदों की कुल पृष्ठीय ऊर्जा तथा बड़ी बूँद की पृष्ठीय ऊर्जा में अनुपात क्या होगा?
आयतन संरक्षण से 43πR3=1000×43πr3⇒r=R10
1000 बूंदों की पृष्ठीय ऊर्जा
=1000×T×4π[R10]2=10(T×4πR2),
बड़ी बूँद की पृष्ठीय ऊर्जा =T×4πR2
पृष्ठीय ऊर्जा में परिवर्तन =36πR2T
अत: बड़ी बूंद बनने में पृष्ठीय ऊर्जा घटती है। अत: ऊर्जा उत्सर्जित होगी।
=10(T×4πR2)T×4πR2=101
उदाहरण 8
पानी की 1000 छोटी बूंदों को मिलाकर एक बड़ी बूँद बनायी जाती है। पृष्ठीय ऊर्जा में क्या परिवर्तन होगा। छोटी बूंदों की कुल पृष्ठीय ऊर्जा तथा बड़ी बूँद की पृष्ठीय ऊर्जा में अनुपात क्या होगा?
आयतन संरक्षण से 43πR3=1000×43πr3⇒r=R10
1000 बूंदों की पृष्ठीय ऊर्जा
=1000×T×4π[R10]2=10(T×4πR2),
बड़ी बूँद की पृष्ठीय ऊर्जा =T×4πR2
पृष्ठीय ऊर्जा में परिवर्तन =36πR2T
अत: बड़ी बूंद बनने में पृष्ठीय ऊर्जा घटती है। अत: ऊर्जा उत्सर्जित होगी।
=10(T×4πR2)T×4πR2=101
उदाहरण 9
पानी की 1mm त्रिज्या की बूँद को 106 समान बूँदो में तोडा जाता है। पानी का पृष्ठ तनाव 72 dyne/cm है। किया गया कार्य ज्ञात कीजिये।
पानी का आयतन संरक्षित रहेगा।
अतः 43πR3=n43πr3
⇒r=Rn1/3
पृष्ठीय क्षेत्रफल में वृद्धि ΔA=n(4πr2)−4πR2
=4π(n1/3−1)R2=4π(100−1)10−6
∴ व्ययित ऊर्जा TΔA
=4π×99×10−16×72×10−3
=89.5×10−6J
उदाहरण 9
पानी की 1mm त्रिज्या की बूँद को 106 समान बूँदो में तोडा जाता है। पानी का पृष्ठ तनाव 72 dyne/cm है। किया गया कार्य ज्ञात कीजिये।
पानी का आयतन संरक्षित रहेगा।
अतः 43πR3=n43πr3
⇒r=Rn1/3
पृष्ठीय क्षेत्रफल में वृद्धि ΔA=n(4πr2)−4πR2
=4π(n1/3−1)R2=4π(100−1)10−6
∴ व्ययित ऊर्जा TΔA
=4π×99×10−16×72×10−3
=89.5×10−6J
काँच की नली में द्रव के मुक्त पृष्ठ की आकृति
जब कोई इस किसी ठोस के स्पर्श में आता है, तो स्पर्श-तल के समीप द्रव का पृष्ठ वक्रीय हो जाता है। वक्रता की प्रकृति द्रव के अणुओं के बीच ससंजक बल तथा द्रव व ठोस के अणुओं के बीच आसंजक-बल के सापेक्ष परिणामों पर निर्भर करती है।
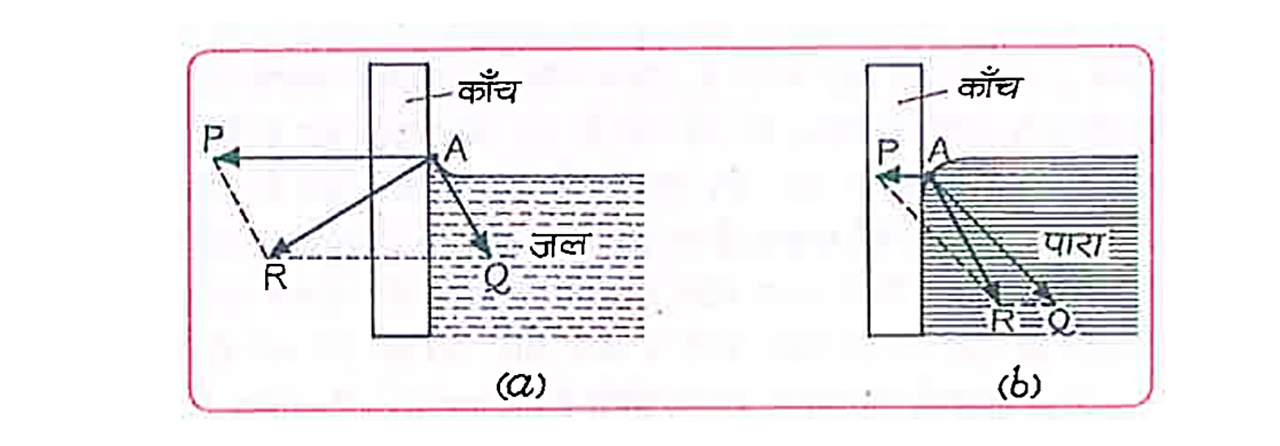
चित्र में जल एक काँच की नली की दीवार के सम्पर्क में दिखाया गया है। माना कि कांच के समीप द्रव के मुक्त पृष्ठ पर एक अणु A है। इस अणु पर दो आकर्षण बल कार्य करते हैं :-
- परिणामी आसंजक-बल P, जो A के समीप वाले ठोस के अणुओं के आकर्षण के कारण A पर कार्य करता है। इसकी दिशा ठोस के पृष्ठ के लम्बवत् है।
- परिणामी संसंजक-बल Q, जो A के समीप द्रव के अन्य अणुओं के आकर्षण के कारण A पर द्रव के अन्दर की ओर एक दिशा में कार्य करता है।
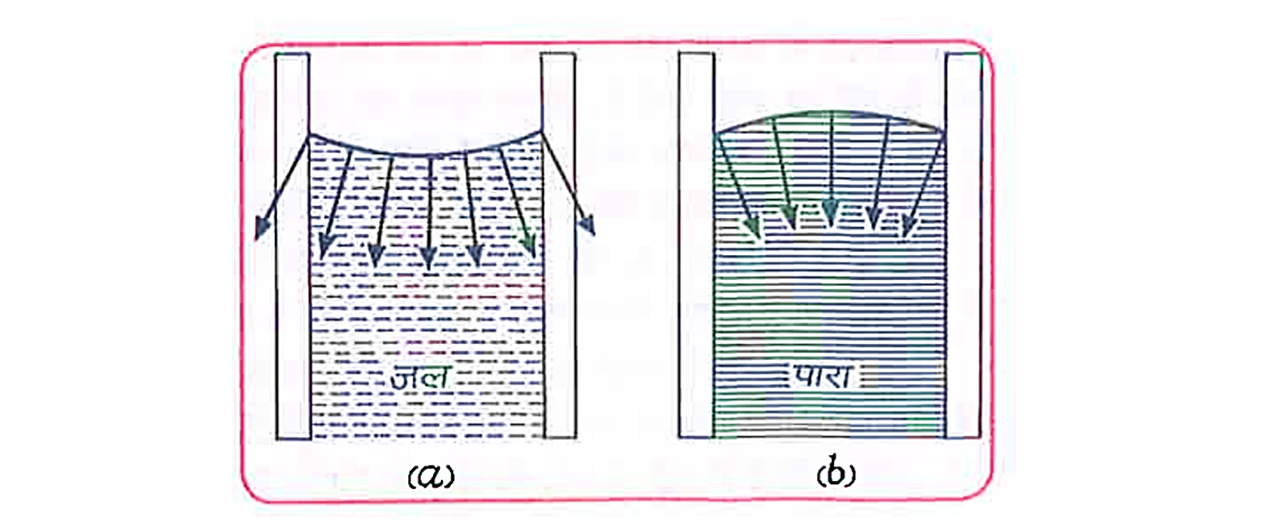
यदि द्रव का मुक्त पृष्ठ साम्यावस्था में है, तो पृष्ठ के किसी अणु पर कार्य करने वाला परिणामी बल पृष्ठ के लम्बवत् होना चाहिए। अतः द्रव का पृष्ठ प्रत्येक स्थान पर परिणामी बल के लम्बवत् हो जाता है। यही कारण है कि काँच की नली में जल का मुक्त पृष्ठ अवतल आकृति धारण कर लेता है तथा पारे का मुक्त पृष्ठ उत्तल आकृति। प्रत्येक दशा में बीच में परिणामी बल ऊर्ध्वाधर होता है, अतः बीच में मुक्त पृष्ठ क्षैतिज होता है
काँच की नली में द्रव के मुक्त पृष्ठ की आकृति
जब कोई इस किसी ठोस के स्पर्श में आता है, तो स्पर्श-तल के समीप द्रव का पृष्ठ वक्रीय हो जाता है। वक्रता की प्रकृति द्रव के अणुओं के बीच ससंजक बल तथा द्रव व ठोस के अणुओं के बीच आसंजक-बल के सापेक्ष परिणामों पर निर्भर करती है।

चित्र में जल एक काँच की नली की दीवार के सम्पर्क में दिखाया गया है। माना कि कांच के समीप द्रव के मुक्त पृष्ठ पर एक अणु A है। इस अणु पर दो आकर्षण बल कार्य करते हैं :-
- परिणामी आसंजक-बल P, जो A के समीप वाले ठोस के अणुओं के आकर्षण के कारण A पर कार्य करता है। इसकी दिशा ठोस के पृष्ठ के लम्बवत् है।
- परिणामी संसंजक-बल Q, जो A के समीप द्रव के अन्य अणुओं के आकर्षण के कारण A पर द्रव के अन्दर की ओर एक दिशा में कार्य करता है।

यदि द्रव का मुक्त पृष्ठ साम्यावस्था में है, तो पृष्ठ के किसी अणु पर कार्य करने वाला परिणामी बल पृष्ठ के लम्बवत् होना चाहिए। अतः द्रव का पृष्ठ प्रत्येक स्थान पर परिणामी बल के लम्बवत् हो जाता है। यही कारण है कि काँच की नली में जल का मुक्त पृष्ठ अवतल आकृति धारण कर लेता है तथा पारे का मुक्त पृष्ठ उत्तल आकृति। प्रत्येक दशा में बीच में परिणामी बल ऊर्ध्वाधर होता है, अतः बीच में मुक्त पृष्ठ क्षैतिज होता है
स्पर्श कोण या सम्पर्क कोण
जब किसी ठोस छड़ को किसी द्रव में डुबाया जाता है तो स्पर्श भाग पर द्रव का पृष्ठ सामान्यत: वक्राकार होता है। कुछ स्थितियों में ऊपर की ओर वक्रीय और कुछ स्थितियों में नीचे की ओर वक्रीय होता है।
किसी ठोस-द्रव युग्म के लिए स्पर्श बिन्दु से द्रव पृष्ठ पर खींची गई स्पर्श रेखा द्रव के अन्दर ठोस की सतह से जो कोण बनाती है, उसे स्पर्श कोण कहते हैं। स्पर्श कोण न्यूनकोण, अधिककोण या समकोण हो सकता है।
स्थिति 1. स्पर्श कोण न्यूनकोण (90°>θ) हो :
जब ठोस के सम्पर्क में द्रव ऊपर की ओर वक्रीय होता है, तो स्पर्श कोण न्यूनकोण होता है। इस स्थिति में द्रव के अणुओं के बीच लगने वाला ससंजक बल द्रव और ठोस के अणुओं के बीच लगने वाले आसंजक बल से कम होता है। अत: द्रव ठोस में चिपक जाता है अर्थात् उसे गीला कर देता है।
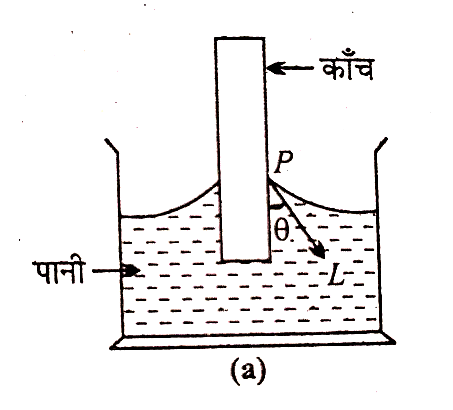
ऐसे द्रव को जब किसी नली में भरा जाता है तो उसका मेनिस्कस (Meniscus) अवतल होता है। पानी और काँच युग्म के लिए स्पर्श कोण न्यूनकोण होता है।
- शुद्ध जल और स्वच्छ काँच के लिए स्पर्श कोण का मान 0° तथा सामान्य जल और स्वच्छ काँच के लिए 8° होता है।
स्थिति 2. स्पर्श कोण अधिककोण (θ>90°) हो :
जब ठोस द्रव के सम्पर्क में नीचे की ओर वक्रीय होता है तो स्पर्श कोण अधिककोण होता है। इस स्थिति में द्रव के अणुओं के बीच लगने वाला ससंजक बल द्रव और ठोस के अणुओं के बीच लगने वाले आसंजक बल से अधिक होता है। अत: द्रव ठोस को गीला नहीं कर पाता। ऐसे द्रव को जब नली में भरा जाता है तो उसका मेनिस्कस उत्तल होता है।
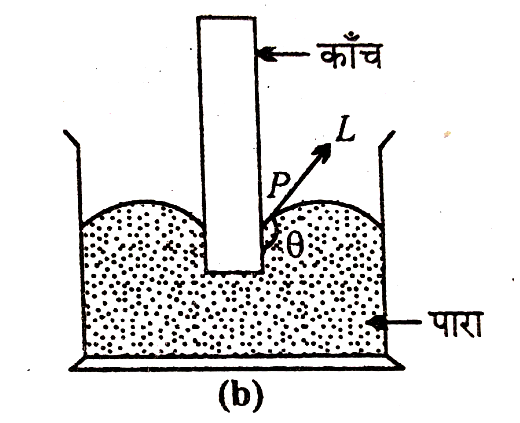
पारा और काँच के लिए स्पर्श कोण अधिककोण होता है। पारा और स्वच्छ काँच के लिए स्पर्श कोण का मान 139° होता है।
स्थिति 3. स्पर्श कोण समकोण (θ=90°) हो :
जब ठोस और द्रव के सम्पर्क में द्रव का पृष्ठ समतल होता है तो स्पर्श कोण का मान समकोण होता है। इस स्थिति में द्रव के अणुओं के बीच लगने वाला ससंजक बल द्रव और ठोस के अणुओं के बीच लगने वाला आसंजक बल के लगभग बराबर होता है। |
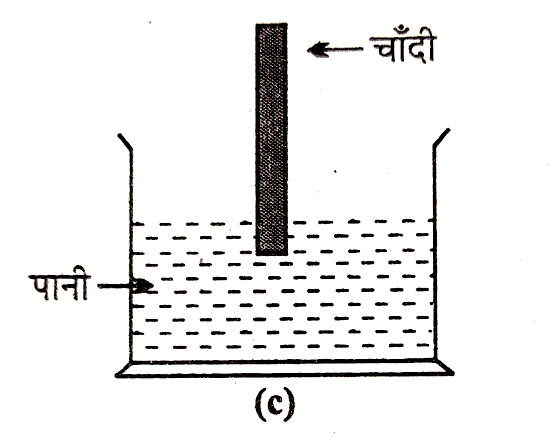
चाँदी की छड़ को पानी में डुबाने पर अथवा चाँदी की नली में पानी को डालने पर स्पर्श कोण समकोण होता है।
स्पर्श कोण की निर्भरता
स्पर्श कोण पर तापमान का प्रभाव :
तापमान बढ़ाने से पृष्ठ तनाव घटता है।
θc∝1T
इसलिए ताप घटाने पर स्पर्श कोण घटता है। स्पर्श कोण पर अशुद्धियों का प्रभाव :
(a) घुलनशील अशुद्धियाँ पृष्ठ तनाव को बढ़ा देती है।
(b) आंशिक घुलनशील अशुद्धियों के कारण पृष्ठ तनाव घटता है। अतः स्पर्श कोण घटेगा।
जल रोधी कारकों का प्रभाव :
जल रोधी कारकों के कारण स्पर्श कोण बढ़ता है। फलस्वरूप न्यून कोण, अधिक-कोण हो जाते हैं।
स्पर्श कोण या सम्पर्क कोण
जब किसी ठोस छड़ को किसी द्रव में डुबाया जाता है तो स्पर्श भाग पर द्रव का पृष्ठ सामान्यत: वक्राकार होता है। कुछ स्थितियों में ऊपर की ओर वक्रीय और कुछ स्थितियों में नीचे की ओर वक्रीय होता है।
किसी ठोस-द्रव युग्म के लिए स्पर्श बिन्दु से द्रव पृष्ठ पर खींची गई स्पर्श रेखा द्रव के अन्दर ठोस की सतह से जो कोण बनाती है, उसे स्पर्श कोण कहते हैं। स्पर्श कोण न्यूनकोण, अधिककोण या समकोण हो सकता है।
स्थिति 1. स्पर्श कोण न्यूनकोण (90°>θ) हो :
जब ठोस के सम्पर्क में द्रव ऊपर की ओर वक्रीय होता है, तो स्पर्श कोण न्यूनकोण होता है। इस स्थिति में द्रव के अणुओं के बीच लगने वाला ससंजक बल द्रव और ठोस के अणुओं के बीच लगने वाले आसंजक बल से कम होता है। अत: द्रव ठोस में चिपक जाता है अर्थात् उसे गीला कर देता है।

ऐसे द्रव को जब किसी नली में भरा जाता है तो उसका मेनिस्कस (Meniscus) अवतल होता है। पानी और काँच युग्म के लिए स्पर्श कोण न्यूनकोण होता है।
- शुद्ध जल और स्वच्छ काँच के लिए स्पर्श कोण का मान 0° तथा सामान्य जल और स्वच्छ काँच के लिए 8° होता है।
स्थिति 2. स्पर्श कोण अधिककोण (θ>90°) हो :
जब ठोस द्रव के सम्पर्क में नीचे की ओर वक्रीय होता है तो स्पर्श कोण अधिककोण होता है। इस स्थिति में द्रव के अणुओं के बीच लगने वाला ससंजक बल द्रव और ठोस के अणुओं के बीच लगने वाले आसंजक बल से अधिक होता है। अत: द्रव ठोस को गीला नहीं कर पाता। ऐसे द्रव को जब नली में भरा जाता है तो उसका मेनिस्कस उत्तल होता है।

पारा और काँच के लिए स्पर्श कोण अधिककोण होता है। पारा और स्वच्छ काँच के लिए स्पर्श कोण का मान 139° होता है।
स्थिति 3. स्पर्श कोण समकोण (θ=90°) हो :
जब ठोस और द्रव के सम्पर्क में द्रव का पृष्ठ समतल होता है तो स्पर्श कोण का मान समकोण होता है। इस स्थिति में द्रव के अणुओं के बीच लगने वाला ससंजक बल द्रव और ठोस के अणुओं के बीच लगने वाला आसंजक बल के लगभग बराबर होता है। |

चाँदी की छड़ को पानी में डुबाने पर अथवा चाँदी की नली में पानी को डालने पर स्पर्श कोण समकोण होता है।
स्पर्श कोण की निर्भरता
स्पर्श कोण पर तापमान का प्रभाव :
तापमान बढ़ाने से पृष्ठ तनाव घटता है।
θc∝1T
इसलिए ताप घटाने पर स्पर्श कोण घटता है। स्पर्श कोण पर अशुद्धियों का प्रभाव :
(a) घुलनशील अशुद्धियाँ पृष्ठ तनाव को बढ़ा देती है।
(b) आंशिक घुलनशील अशुद्धियों के कारण पृष्ठ तनाव घटता है। अतः स्पर्श कोण घटेगा।
जल रोधी कारकों का प्रभाव :
जल रोधी कारकों के कारण स्पर्श कोण बढ़ता है। फलस्वरूप न्यून कोण, अधिक-कोण हो जाते हैं।
द्रव के पृष्ठ की आकृति
जब कोई द्रव किसी ठोस सतह के सम्पर्क में आता है तो स्पर्श तल के समीप द्रव का पृष्ठ वक्रीय हो जाता है। वक्रता की प्रकृति (अवतल या उत्तल) द्रव के अणुओं के बीच ससंजक बल तथा द्रव व ठोस के अणुओं के बीच आसंजक बल के आपेक्षिक परिमार्णों पर निर्भर करती है। काँच के पात्र की दीवार के समीप द्रव की वह मुक्त पृष्ठ, जो कि पृष्ठ तनाव के कारण वक्रीय है को नव चन्द्रक कहते हैं। ससंजक बल द्रव सतह से 45° के कोण पर कार्य करता है। जबकि आसंजक बल ठोस सतह के लम्बवत दिशा में कार्य करता है।
द्रव के पृष्ठ की आकृति
जब कोई द्रव किसी ठोस सतह के सम्पर्क में आता है तो स्पर्श तल के समीप द्रव का पृष्ठ वक्रीय हो जाता है। वक्रता की प्रकृति (अवतल या उत्तल) द्रव के अणुओं के बीच ससंजक बल तथा द्रव व ठोस के अणुओं के बीच आसंजक बल के आपेक्षिक परिमार्णों पर निर्भर करती है। काँच के पात्र की दीवार के समीप द्रव की वह मुक्त पृष्ठ, जो कि पृष्ठ तनाव के कारण वक्रीय है को नव चन्द्रक कहते हैं। ससंजक बल द्रव सतह से 45° के कोण पर कार्य करता है। जबकि आसंजक बल ठोस सतह के लम्बवत दिशा में कार्य करता है।
गोलीय पृष्ठ पर दाब आधिक्य
किसी पात्र में द्रव का पृष्ठ अवतल, उत्तल अथवा समतल हो सकता है। प्रत्येक स्थिति में मानलो द्रव के मेनिस्कस पर एक अणु M है। इस अणु पर पृष्ठ तनाव के कारण द्रव के पृष्ठ की स्पर्श रेखीय दिशा में सभी दिशाओं में बल कार्य करता है।
(i) यदि द्रव का पृष्ठ अवतल है तो अणु M पर पृष्ठ तनाव के कारण पृष्ठ के लंबवत् एक नेट बल F ऊपर की ओर कार्य करेगा।
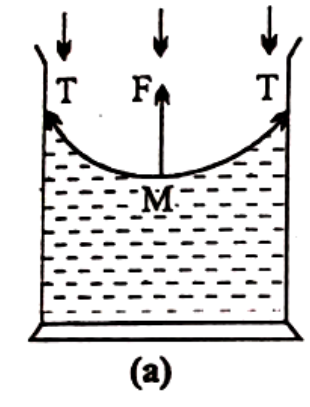
यह अणु संतुलन में उसी स्थिति में रह पायेगा जबकि पृष्ठ के बाहर अर्थात् अवतल भाग की ओर दाब अधिक हो।
(ii) यदि द्रव का पृष्ठ उत्तल है तो अणु M पर पृष्ठ तनाव के कारण एक नेट बल F पृष्ठ के लम्बवत् अन्दर की ओर कार्य करेगा।
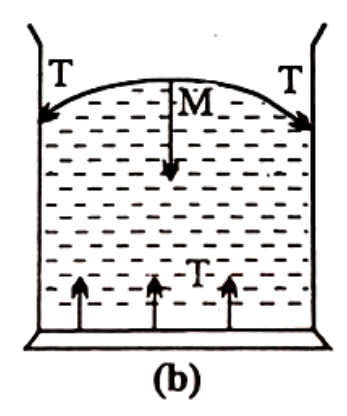
यह अणु संतुलन में उसी स्थिति में रहेगा जबकि पृष्ठ से द्रव की ओर अर्थात् अवतल भाग की ओर दाब अधिक हो।
(iii) यदि द्रव का पृष्ठ समतल है तो अणु M पर पृष्ठ तनाव के कारण पृष्ठ से बाहर या अन्दर की ओर पृष्ठ के लम्बवत् नेट बल शून्य होगा।

अत: द्रव पृष्ठ के बाहर और अन्दर दाब एकसमान होगा।
इस प्रकार यदि द्रव का पृष्ठ गोलीय है तो पृष्ठ की संतुलन अवस्था में द्रव पृष्ठ के अवतल भाग की ओर का दाब उत्तल भाग की ओर के दाब से अधिक होता है। यह दाबान्तर द्रव के पृष्ठ तनाव और पृष्ठ की वक्रता त्रिज्या पर निर्भर करता है।
गोलीय पृष्ठ पर दाब आधिक्य
किसी पात्र में द्रव का पृष्ठ अवतल, उत्तल अथवा समतल हो सकता है। प्रत्येक स्थिति में मानलो द्रव के मेनिस्कस पर एक अणु M है। इस अणु पर पृष्ठ तनाव के कारण द्रव के पृष्ठ की स्पर्श रेखीय दिशा में सभी दिशाओं में बल कार्य करता है।
(i) यदि द्रव का पृष्ठ अवतल है तो अणु M पर पृष्ठ तनाव के कारण पृष्ठ के लंबवत् एक नेट बल F ऊपर की ओर कार्य करेगा।

यह अणु संतुलन में उसी स्थिति में रह पायेगा जबकि पृष्ठ के बाहर अर्थात् अवतल भाग की ओर दाब अधिक हो।
(ii) यदि द्रव का पृष्ठ उत्तल है तो अणु M पर पृष्ठ तनाव के कारण एक नेट बल F पृष्ठ के लम्बवत् अन्दर की ओर कार्य करेगा।

यह अणु संतुलन में उसी स्थिति में रहेगा जबकि पृष्ठ से द्रव की ओर अर्थात् अवतल भाग की ओर दाब अधिक हो।
(iii) यदि द्रव का पृष्ठ समतल है तो अणु M पर पृष्ठ तनाव के कारण पृष्ठ से बाहर या अन्दर की ओर पृष्ठ के लम्बवत् नेट बल शून्य होगा।

अत: द्रव पृष्ठ के बाहर और अन्दर दाब एकसमान होगा।
इस प्रकार यदि द्रव का पृष्ठ गोलीय है तो पृष्ठ की संतुलन अवस्था में द्रव पृष्ठ के अवतल भाग की ओर का दाब उत्तल भाग की ओर के दाब से अधिक होता है। यह दाबान्तर द्रव के पृष्ठ तनाव और पृष्ठ की वक्रता त्रिज्या पर निर्भर करता है।
द्रव के बूँद तथा साबुन के बुलबुले के अन्दर दाब आधिक्य
द्रव के बूँद के अन्दर दाब आधिक्य :
मानलो द्रव बूंद की त्रिज्या R तथा उसके अंदर दाब आधिक्य P है। इस दाब आधिक्य के कारण बूँद के पृष्ठ के लम्बवत् बाहर की ओर एक बल कार्य करता है। फलस्वरूप मानलो बूँद की त्रिज्या R से बढ़कर (R+△R) हो जाती है।
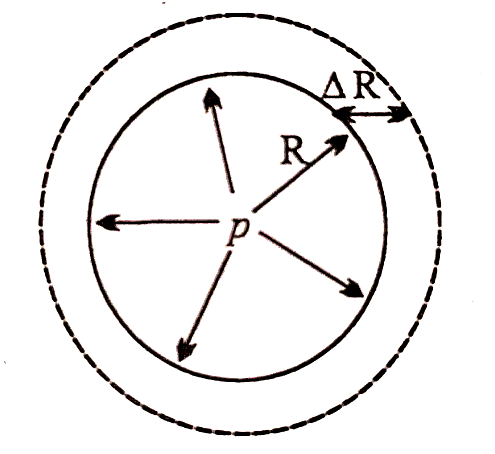
दाब आधिक्य के द्वारा किया गया कार्य गणना
W = बल × दूरी = दाब आधिक्य × क्षेत्रफल × दूरी
या
बूँद के पृष्ठीय क्षेत्रफल में वृद्धि
या
या
△R का मान बहुत कम होता है। अत: (△R)2 की उपेक्षा करने पर,
किन्तु W=T.△A अत: समीकरण (1) और (2) से,
या
यही द्रव बूँद के दाब आधिक्य के लिए व्यंजक है।
साबुन के बुलबुले के अन्दर दाब आधिक्य :
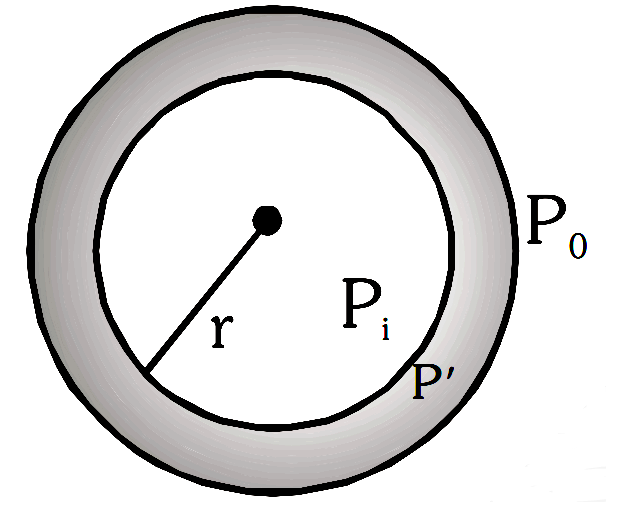
चूंकि साबुन के बुलबुले में दो सतह होती है इसलिये बूंद की तुलना में इसमें दाब आधिक्य दुगना होगा। अतः,
बाहरी सतह के लिए दाब आधिक्य होगा,
तथा बाहरी परत के लिए दाब आधिक्य होगा,
साबुन के बुलबुले का कुल दाब आधिक्य दोनों परतों के दाब आधिक्य के योग के बराबर होगा अर्थात,
द्रव के बूँद तथा साबुन के बुलबुले के अन्दर दाब आधिक्य
द्रव के बूँद के अन्दर दाब आधिक्य :
मानलो द्रव बूंद की त्रिज्या R तथा उसके अंदर दाब आधिक्य P है। इस दाब आधिक्य के कारण बूँद के पृष्ठ के लम्बवत् बाहर की ओर एक बल कार्य करता है। फलस्वरूप मानलो बूँद की त्रिज्या R से बढ़कर (R+△R) हो जाती है।

दाब आधिक्य के द्वारा किया गया कार्य गणना
W = बल × दूरी = दाब आधिक्य × क्षेत्रफल × दूरी
या
बूँद के पृष्ठीय क्षेत्रफल में वृद्धि
या
या
△R का मान बहुत कम होता है। अत: (△R)2 की उपेक्षा करने पर,
किन्तु W=T.△A अत: समीकरण (1) और (2) से,
या
यही द्रव बूँद के दाब आधिक्य के लिए व्यंजक है।
साबुन के बुलबुले के अन्दर दाब आधिक्य :

चूंकि साबुन के बुलबुले में दो सतह होती है इसलिये बूंद की तुलना में इसमें दाब आधिक्य दुगना होगा। अतः,
बाहरी सतह के लिए दाब आधिक्य होगा,
तथा बाहरी परत के लिए दाब आधिक्य होगा,
साबुन के बुलबुले का कुल दाब आधिक्य दोनों परतों के दाब आधिक्य के योग के बराबर होगा अर्थात,
केशनली और केशिकात्व
दोनों सिरों पर खुली बारीक सुराख की कांच की नली को केशनली कहते हैं। केशनली में किसी द्रव के ऊपर चढ़ने या नीचे गिरने का गुणधर्म केशिकात्व कहलाता है। बारीक सुराख की काँच की नली (केशनली) में द्रव के ऊपर चढ़ने या नीचे गिरने को केशिकात्व क्रिया कहते हैं। उदाहरण
- कैरासीन
- फाउंटेन पेन के निब के मध्य के रिक्त स्थान को कार्यप्रणाली केशिकात्व कारण ही है।
केशकीय ऊँचाई की गणना :

चित्रानुसार जब एक केशनली को पहले द्रव में डुबोते है तो द्रव वक्रीय पृष्ठ रूप में दीवारों पर चढ़ता है। माना नवचन्द्रक (अर्थात केशनली में बने द्रव का आकार) की त्रिज्या R तथा केशनली की त्रिज्या r है। माना नवचन्द्रक केशनली से θc कोण बनाता है तथा केशनली में द्रव का तनाव T, द्रव का घनत्व ρ है तथा यह h ऊँचाई तक चढ़ता हैं।
अब क्षैतिज तल में दो बिंदु A व B चित्रानुसार मानते है। तब पास्कल के नियम से
अब नवचंद्रक पर कोई बिंदु C है तब Patm व PC दाब इसके क्रमश: अवतल तथा उत्तल सतह पर लगते है। अतः
यहाँ PC−Patm=0 अतः,
या
केशनली और केशिकात्व
दोनों सिरों पर खुली बारीक सुराख की कांच की नली को केशनली कहते हैं। केशनली में किसी द्रव के ऊपर चढ़ने या नीचे गिरने का गुणधर्म केशिकात्व कहलाता है। बारीक सुराख की काँच की नली (केशनली) में द्रव के ऊपर चढ़ने या नीचे गिरने को केशिकात्व क्रिया कहते हैं। उदाहरण
- कैरासीन
- फाउंटेन पेन के निब के मध्य के रिक्त स्थान को कार्यप्रणाली केशिकात्व कारण ही है।
केशकीय ऊँचाई की गणना :

चित्रानुसार जब एक केशनली को पहले द्रव में डुबोते है तो द्रव वक्रीय पृष्ठ रूप में दीवारों पर चढ़ता है। माना नवचन्द्रक (अर्थात केशनली में बने द्रव का आकार) की त्रिज्या R तथा केशनली की त्रिज्या r है। माना नवचन्द्रक केशनली से θc कोण बनाता है तथा केशनली में द्रव का तनाव T, द्रव का घनत्व ρ है तथा यह h ऊँचाई तक चढ़ता हैं।
अब क्षैतिज तल में दो बिंदु A व B चित्रानुसार मानते है। तब पास्कल के नियम से
अब नवचंद्रक पर कोई बिंदु C है तब Patm व PC दाब इसके क्रमश: अवतल तथा उत्तल सतह पर लगते है। अतः
यहाँ PC−Patm=0 अतः,
या
उदाहरण 10
सिद्ध करो कि यदि दो बुलबुले जिनकी त्रिज्याएँ r1 तथा r2 है ,मिलकर एक बुलबुला बनाते है तो उनकी त्रिज्या r=√r21+r22 होगी
जब दो साबुन के बुलबुले आपस में मिलते हैं तो हवा के कुल अणुओं की संख्या नियत रहेगी तथा तापमान भी नियत है।
अत: n1+n2=n⇒P1V1+P2V2=PV
⇒4Tr1(43πr31)+4Tr2(43πr32)
⇒r=√r21+r22
उदाहरण 10
सिद्ध करो कि यदि दो बुलबुले जिनकी त्रिज्याएँ r1 तथा r2 है ,मिलकर एक बुलबुला बनाते है तो उनकी त्रिज्या r=√r21+r22 होगी
जब दो साबुन के बुलबुले आपस में मिलते हैं तो हवा के कुल अणुओं की संख्या नियत रहेगी तथा तापमान भी नियत है।
अत: n1+n2=n⇒P1V1+P2V2=PV
⇒4Tr1(43πr31)+4Tr2(43πr32)
⇒r=√r21+r22
उदाहरण 11
सिद्ध करो कि यदि दो बुलबुले जिनकी त्रिज्याएं r1 तथा r2(r1<r2) है , तब r=r1r2r1−r2 होगी।
∴r1<r2
∴P1>P2 बुलबुले का उभयनिष्ठ भाग साम्यावस्था में रहेगा
⇒P1−P2=4Tr
⇒4Tr1−4Tr1=4Tr
⇒r=r1r2r1−r2
उदाहरण 11
सिद्ध करो कि यदि दो बुलबुले जिनकी त्रिज्याएं r1 तथा r2(r1<r2) है , तब r=r1r2r1−r2 होगी।
∴r1<r2
∴P1>P2 बुलबुले का उभयनिष्ठ भाग साम्यावस्था में रहेगा
⇒P1−P2=4Tr
⇒4Tr1−4Tr1=4Tr
⇒r=r1r2r1−r2
उदाहरण 12
पानी के अन्दर हवा के बुलबुले की त्रिज्या 0.1 mm है तथा पानी की सतह के 10cm नीचे बनता है, जब वायुमण्डलीय दाब 1.013×105Pa हो तो बुलबुले के अन्दर कुल दाब क्या होगा? (पानी का पृष्ठ तनाव =73×10−3N/m)
दाब आधिक्य Pn=Patm+hdg+2Tr
=(1.013×105)+(10×10−2×9.8)
+2×73×10−30.1×10−3
=101300+980+1460=103740
=1.037×105Pa
उदाहरण 12
पानी के अन्दर हवा के बुलबुले की त्रिज्या 0.1 mm है तथा पानी की सतह के 10cm नीचे बनता है, जब वायुमण्डलीय दाब 1.013×105Pa हो तो बुलबुले के अन्दर कुल दाब क्या होगा? (पानी का पृष्ठ तनाव =73×10−3N/m)
दाब आधिक्य Pn=Patm+hdg+2Tr
=(1.013×105)+(10×10−2×9.8)
+2×73×10−30.1×10−3
=101300+980+1460=103740
=1.037×105Pa
उदाहरण 13
1×10−3m व्यास की एक केशनली में चढ़े पानी के स्तम्भ की ऊँचाई की गणना कीजिए। [दिया है : पानी का पृष्ठ तनाव 0.072 N/m, स्पर्श कोण 0∘, पानी का घनत्व 1000kg/m3 एवं g=9.8m/s2]
केशनली में चढ़े द्रव की ऊँचाई
h=2Tcosθrρg
=2×0.072×cos0∘5×10−4×1000×9.8m
=2.94×10−2m
उदाहरण 13
1×10−3m व्यास की एक केशनली में चढ़े पानी के स्तम्भ की ऊँचाई की गणना कीजिए। [दिया है : पानी का पृष्ठ तनाव 0.072 N/m, स्पर्श कोण 0∘, पानी का घनत्व 1000kg/m3 एवं g=9.8m/s2]
केशनली में चढ़े द्रव की ऊँचाई
h=2Tcosθrρg
=2×0.072×cos0∘5×10−4×1000×9.8m
=2.94×10−2m
उदाहरण 14
एक केशनली में जल 20 mm ऊँचाई तक चढ़ता है। यदि केशनली की त्रिज्या को इसके प्रारम्भिक मान का एक तिहाई करते है तब केशनली में चढ़े जल की ऊँचाई का नया मान होगा?
∴h2h1=r1r2=1(1/3)=3
⇒h2=3h1=3×20mm=60mm
उदाहरण 14
एक केशनली में जल 20 mm ऊँचाई तक चढ़ता है। यदि केशनली की त्रिज्या को इसके प्रारम्भिक मान का एक तिहाई करते है तब केशनली में चढ़े जल की ऊँचाई का नया मान होगा?
∴h2h1=r1r2=1(1/3)=3
⇒h2=3h1=3×20mm=60mm
उदाहरण 15
एक खोखले गोले के पेंदे में एक सूक्ष्म छिद्र है। इस गोले को अधिकतम 30 cm की गहराई तक ले जाने पर इसके छिद्र में पानी प्रवेश नहीं कर पाता है। यदि पानी का पृष्ठ तनाव 75 dyne/cm हो तो छिद्र की त्रिज्या ज्ञात कीजिए। (g=10m/s2)
छिद्र की त्रिज्या
r=2Thdg=2×75×10−330×10−2×103×10
=5×10−5m
उदाहरण 15
एक खोखले गोले के पेंदे में एक सूक्ष्म छिद्र है। इस गोले को अधिकतम 30 cm की गहराई तक ले जाने पर इसके छिद्र में पानी प्रवेश नहीं कर पाता है। यदि पानी का पृष्ठ तनाव 75 dyne/cm हो तो छिद्र की त्रिज्या ज्ञात कीजिए। (g=10m/s2)
छिद्र की त्रिज्या
r=2Thdg=2×75×10−330×10−2×103×10
=5×10−5m
उदाहरण 16
एक U-नली की उर्ध्वाधर भुजाएँ पानी से आंशिक रूप से भरी हुई है। यदि भुजाओं का आन्तरिक व्यास क्रमश: 1×10−2m और 1×10−4m हो तो दोनों भुजाओं के पानी की ऊँचाई में अंतर क्या होगा ? (पानी का पृष्ठ तनाव 0.07 N/m है।)
माना r1 व r2 त्रिज्या वाली शाखा में पानी की ऊँचाई h1 व h2 है
तब h1=2Tcosθr1dg
=2×0.07×cos0∘0.5×10−4×1000×9.8
=2.8×10−3m=0.028×10−1m
इसी तरह h2=2×0.07×cos0∘0.5×10−2×1000×9.8
=2.8×10−1m
इसलिये पानी की ऊँचाई में अन्तर
=h2−h1=(2.8=0.028)×10−1m
=2.772×10−1m=0.277m
उदाहरण 16
एक U-नली की उर्ध्वाधर भुजाएँ पानी से आंशिक रूप से भरी हुई है। यदि भुजाओं का आन्तरिक व्यास क्रमश: 1×10−2m और 1×10−4m हो तो दोनों भुजाओं के पानी की ऊँचाई में अंतर क्या होगा ? (पानी का पृष्ठ तनाव 0.07 N/m है।)
माना r1 व r2 त्रिज्या वाली शाखा में पानी की ऊँचाई h1 व h2 है
तब h1=2Tcosθr1dg
=2×0.07×cos0∘0.5×10−4×1000×9.8
=2.8×10−3m=0.028×10−1m
इसी तरह h2=2×0.07×cos0∘0.5×10−2×1000×9.8
=2.8×10−1m
इसलिये पानी की ऊँचाई में अन्तर
=h2−h1=(2.8=0.028)×10−1m
=2.772×10−1m=0.277m
