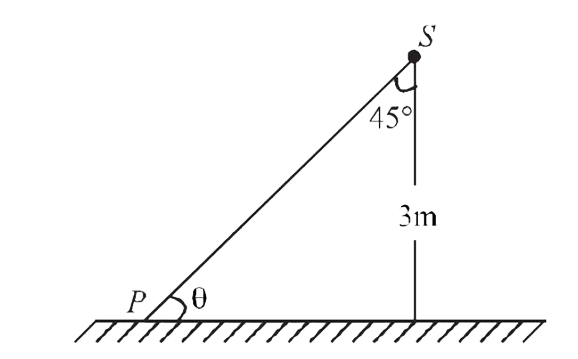
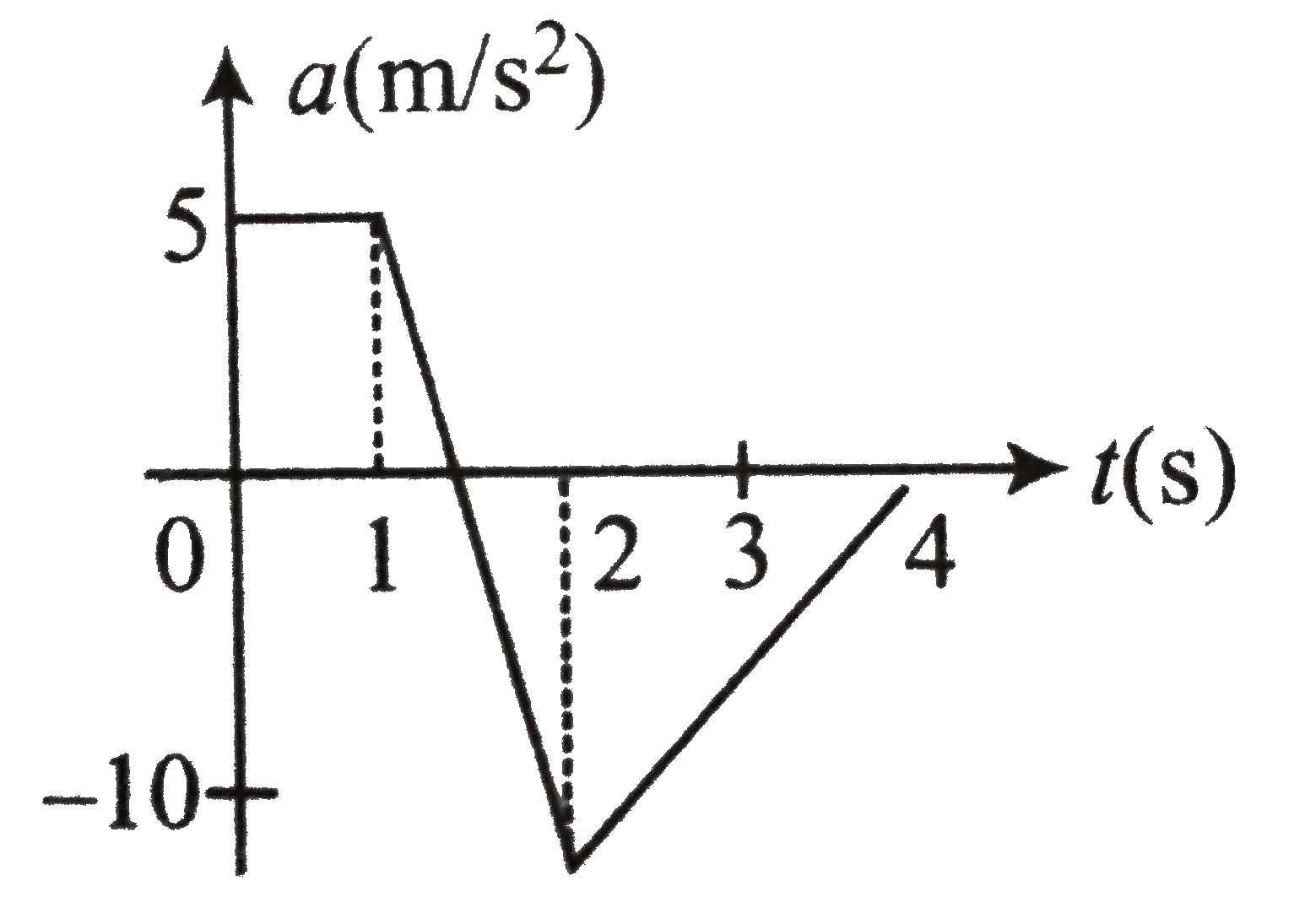Linked Comprehension Type from CENGAGE PHYSICS (ENGLISH) MISCELLANEOUS KINEMATICS for Class 11
| Class 11 | PHYSICS |
| Chapter | MISCELLANEOUS KINEMATICS |
| CENGAGE PHYSICS (ENGLISH) | Linked Comprehension Type |
| Medium | English |
| Academic Year | 2023-2024 |
Question 13
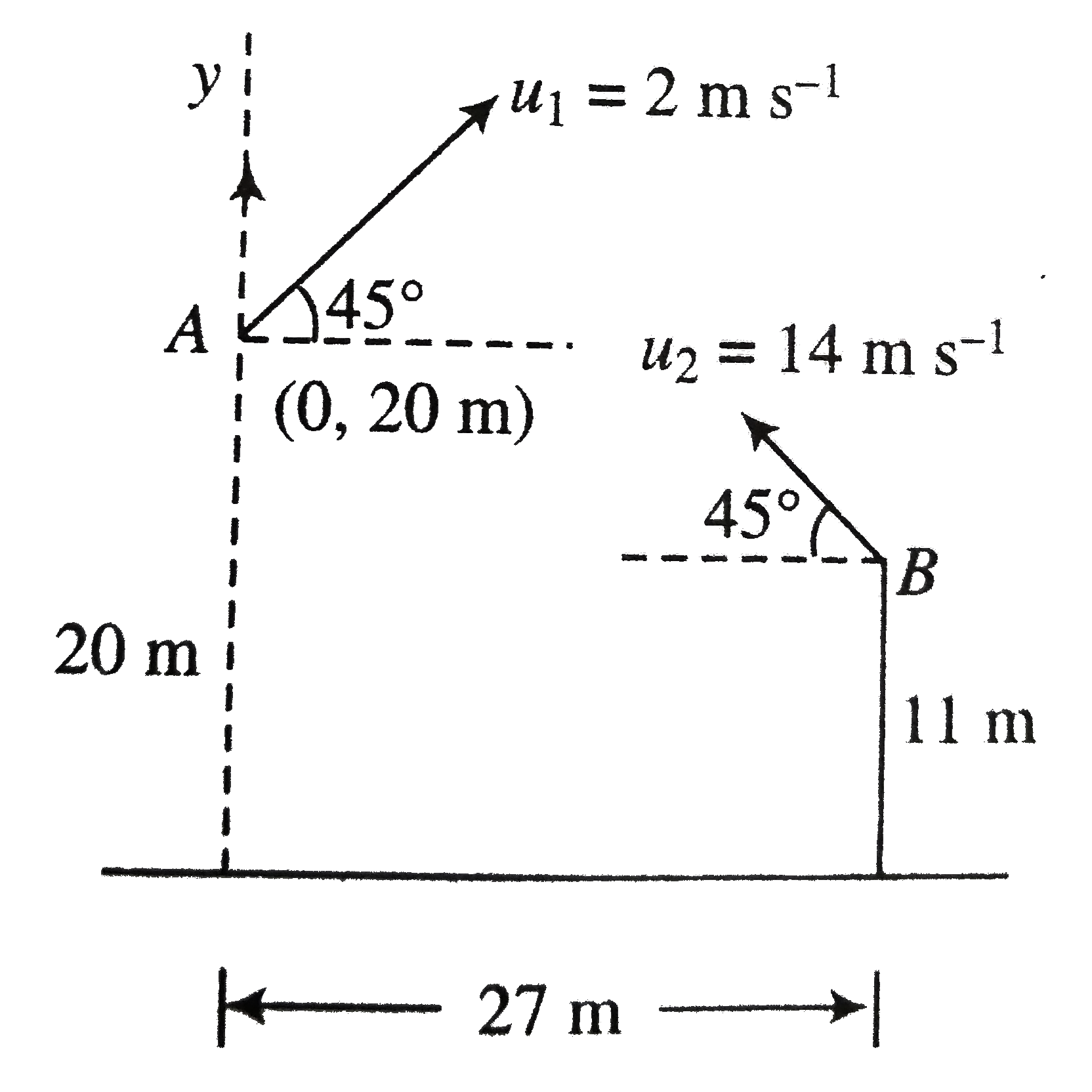
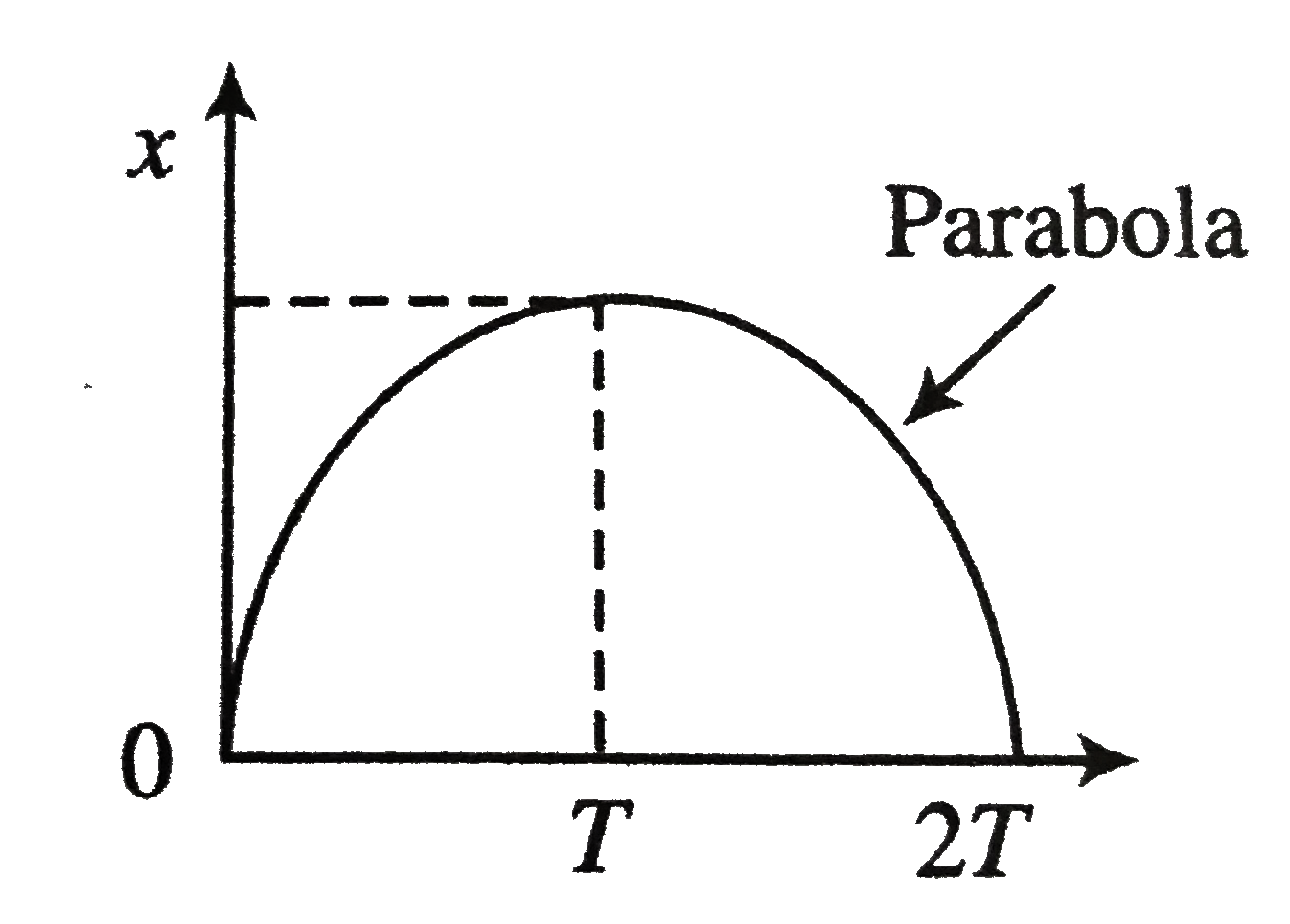
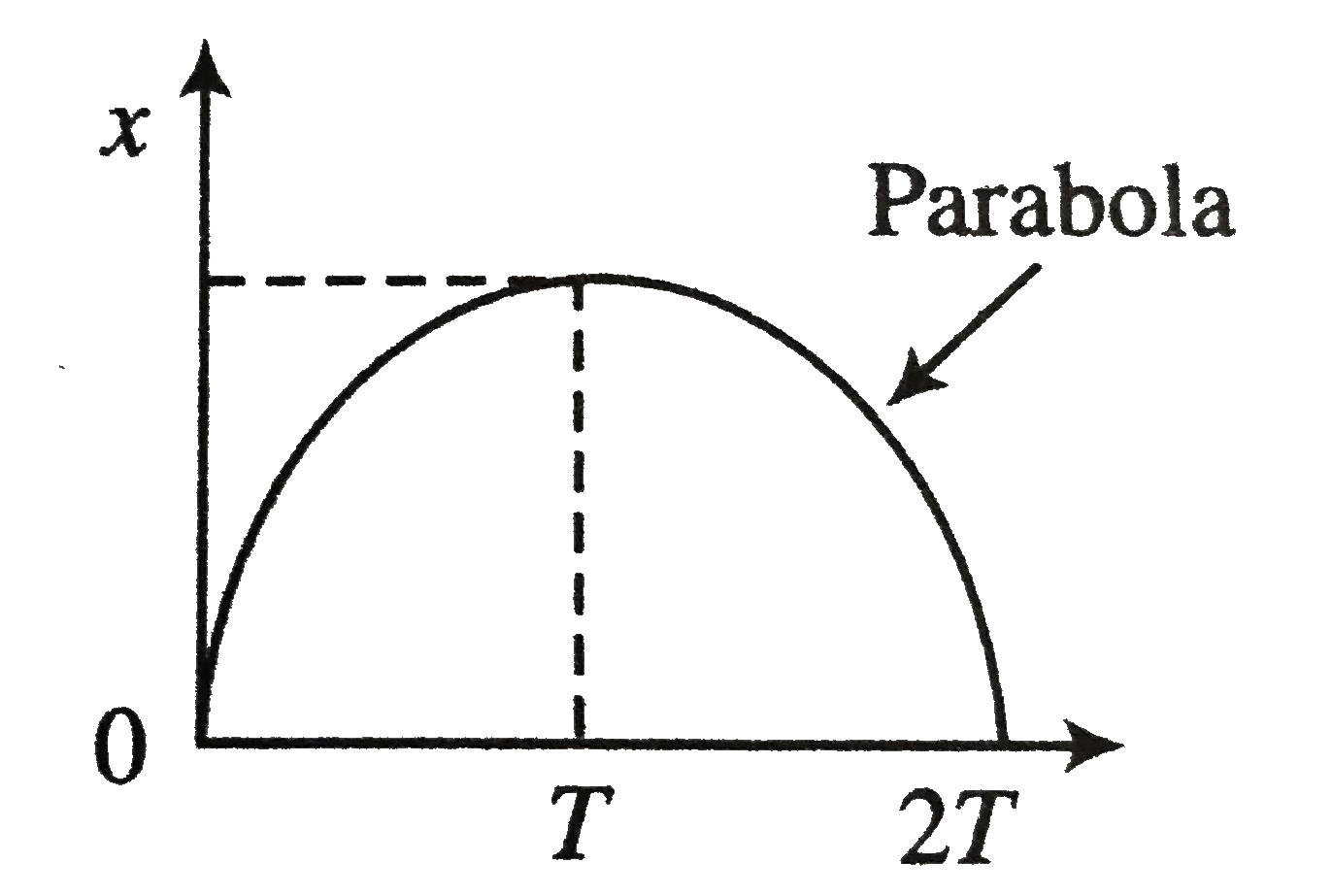
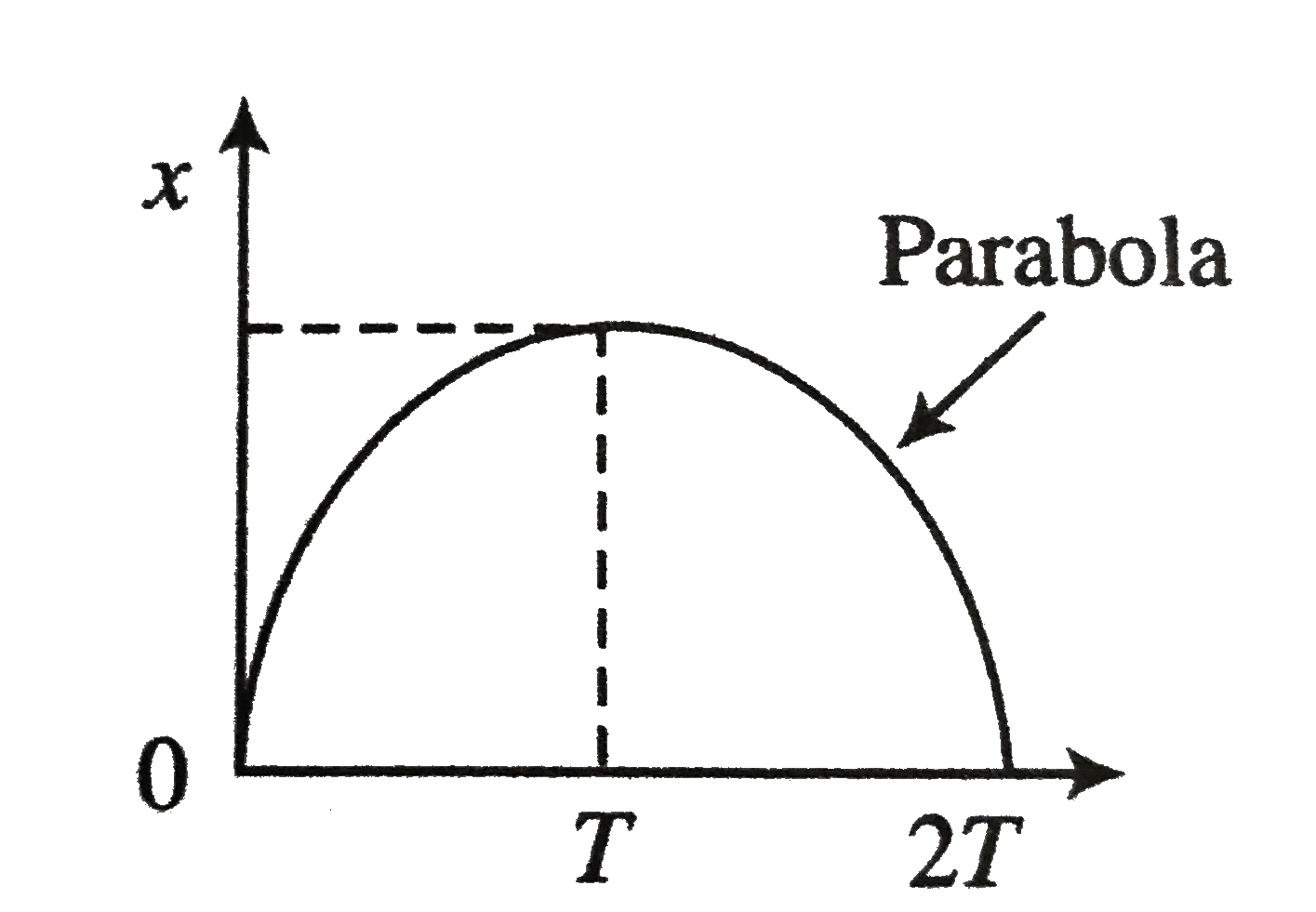
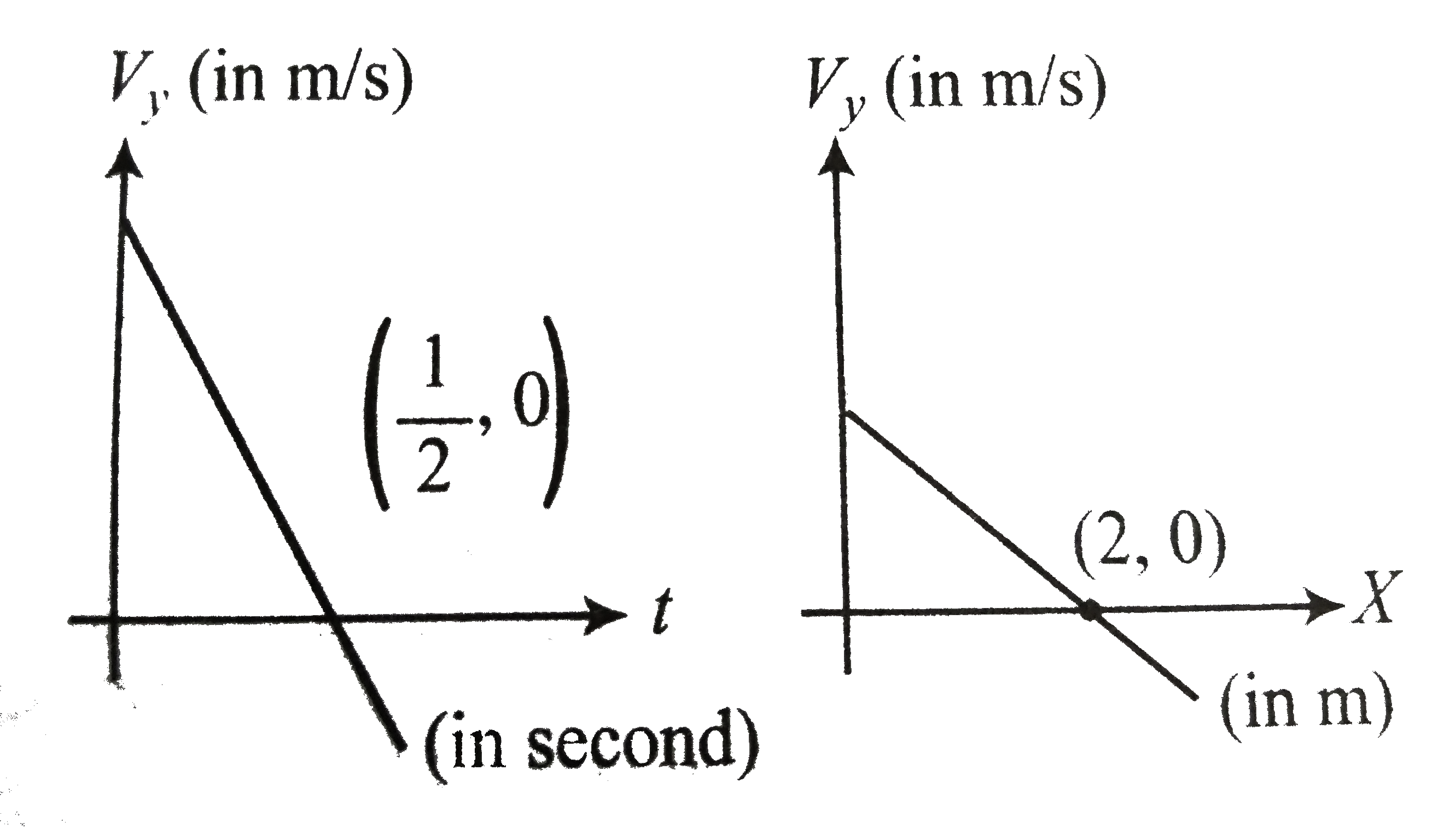
Two trains, which are moving along different tracks in opposite directions, are put on the same track due to a mistake. Their drivers, on noticing the mistake, start slowing down the trains when the trains are 300 m apart. Graphs given in figure show their velocities as function of time as the trains slow down. The separation between the trains when both have stopped is
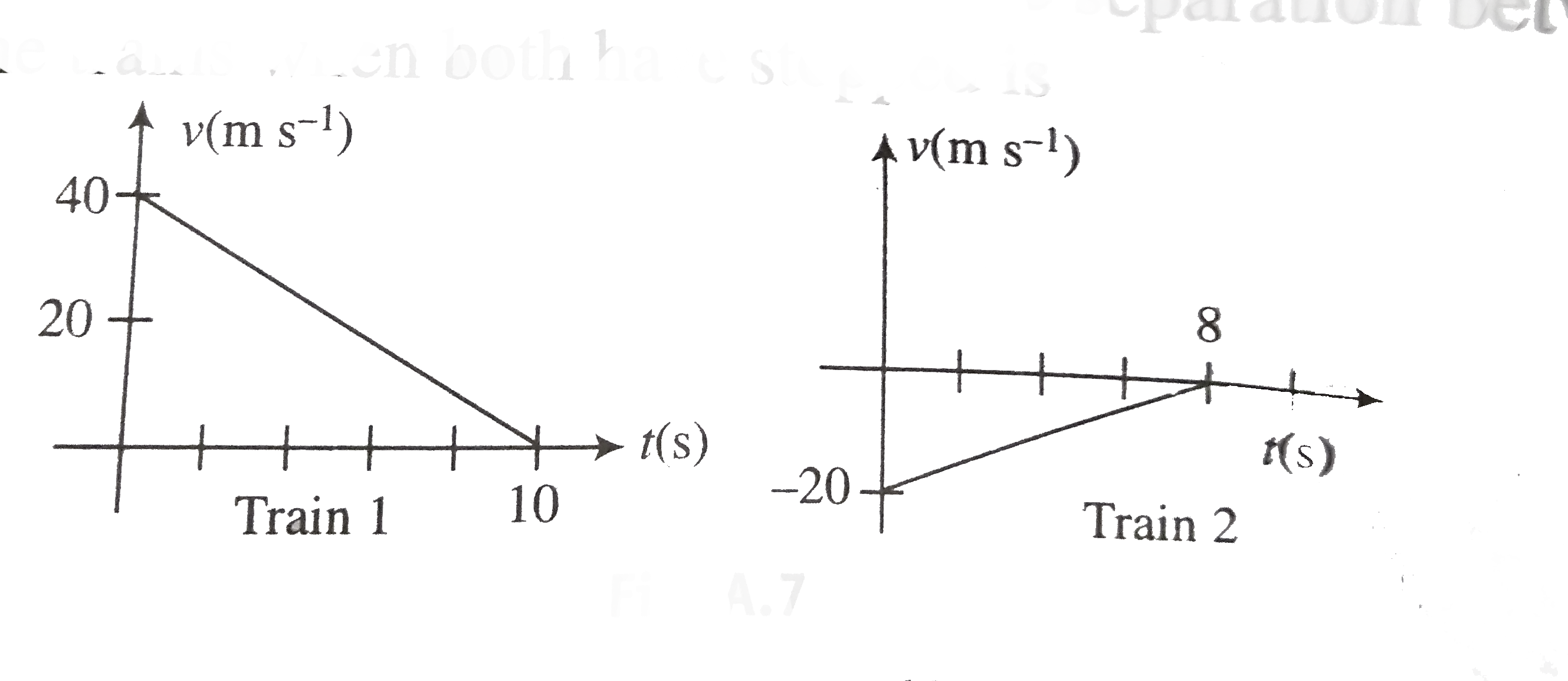 View Solution
View SolutionQuestion 17
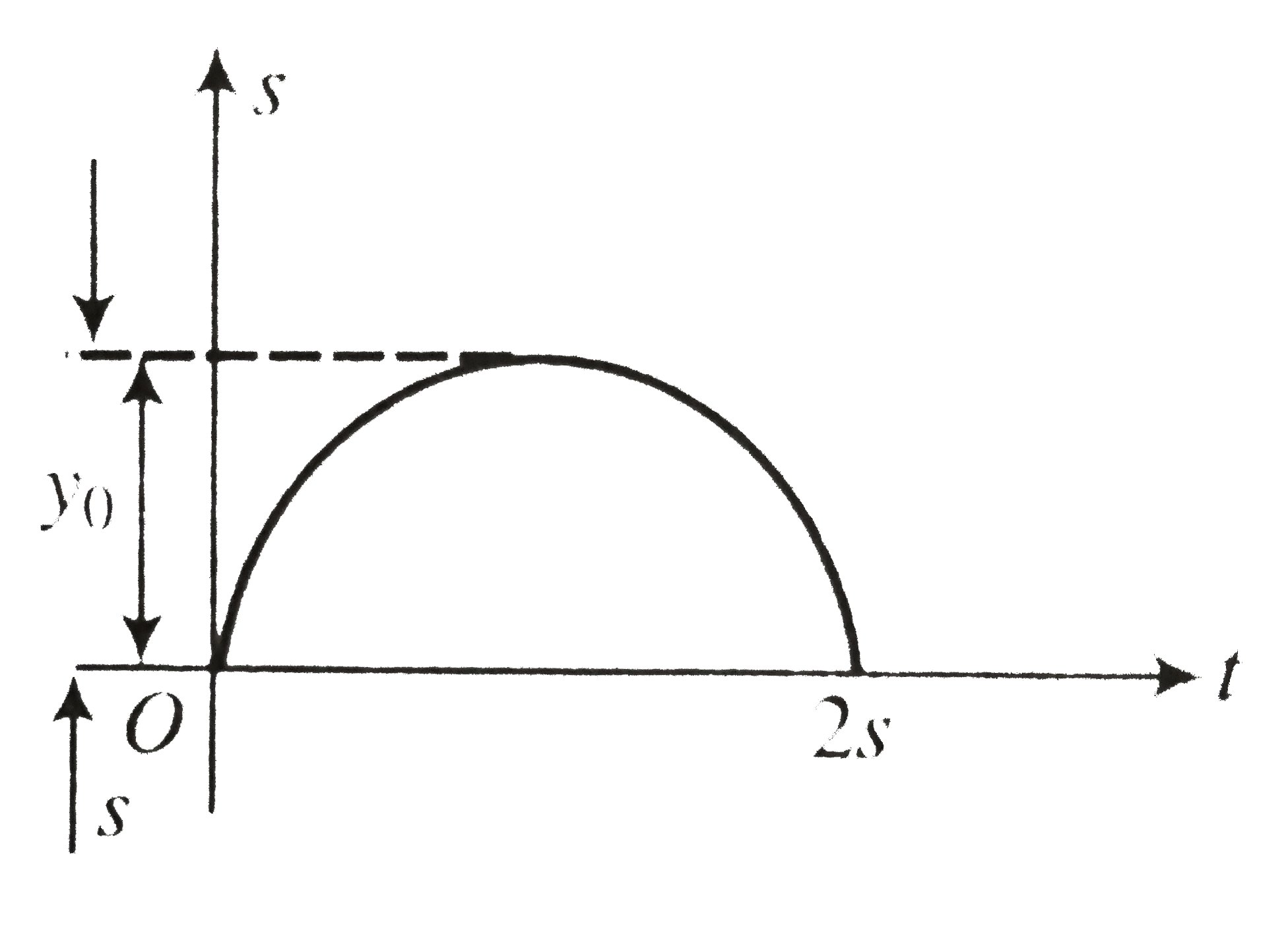
Two boys P and Q are playing on a river bank. P plans to swim across the river directly and come back. Q plans to swim downstream by a length equal to the width of the river and then come back. Both of them bet each other, claiming that the boy succeeding in less time will win. Assuming the swimming rate of both P and Q to the same, it can be concluded that View SolutionQuestion 18
A man holds an umbrella at 30∘ with the vertical to keep himself dry. He, then, runs at a speed of 10ms−1, and find the rain drops to be hitting vertically. Study the following statement and find the correct options.
i. Velocity of rain w.r.t. Earth is 20ms−1
ii. Velocity of rain w.r.t. man is 10√3ms−1.
iii. Velocity of rain w.r.t. Earth is 30ms−1
iv. Velocity of rain w.r. t. man is 10√2ms−1 . View SolutionQuestion 19
Rain appears to fall vertically to a man walking at 3kmh−1, but when he changes his speed to double, the rain appears to fall at 45∘ with vertical. Study the following statements and find which of them are correct.
i. Velocity of rain is 2(√3)kmh−1.
ii. The angle of fall of rain (with vertical) is θ=tan−1(1√2).
iii. The angle of fall of rain (with vertical) is θ=sin−1(1√2).
iv. Velocity of rain is 3(√2)kmh−1 . View SolutionQuestion 22
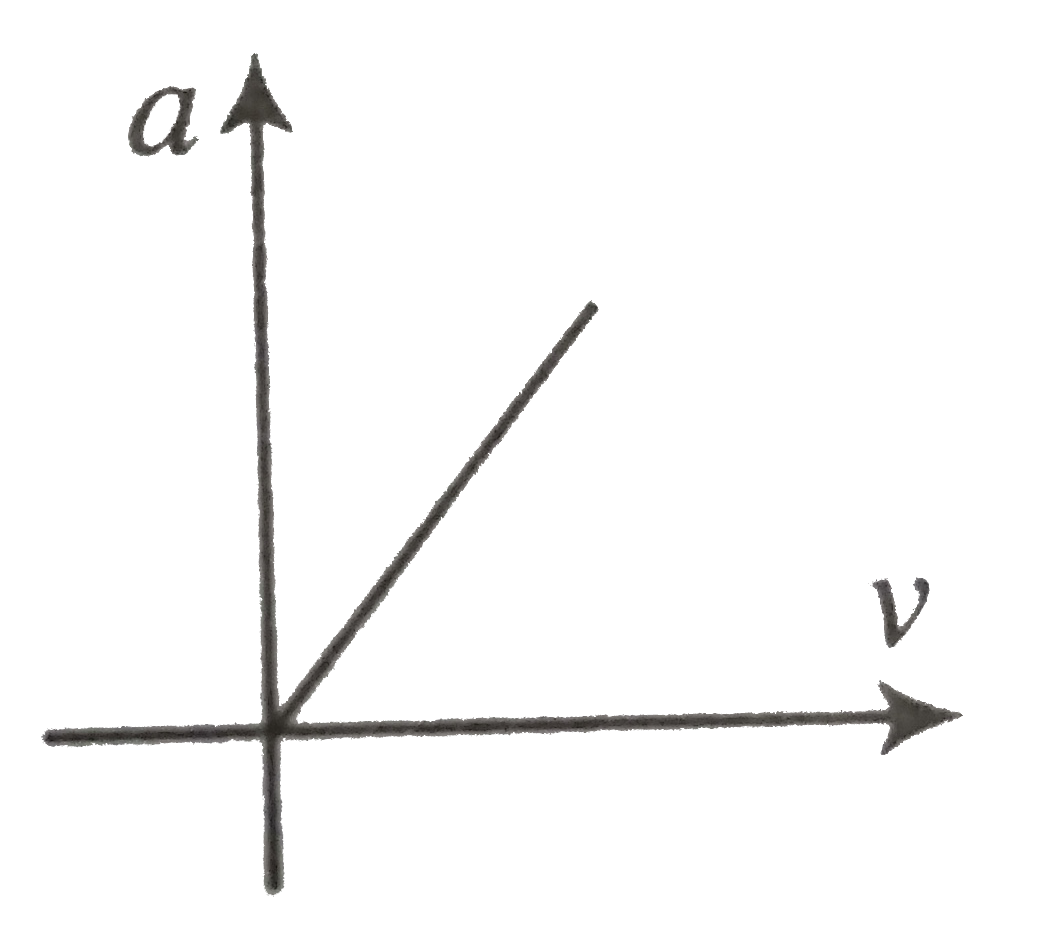
A body A is thrown vertically upwards with such a velocity that it reaches a maximum height of h. Simultaneously, another body B is dropped from height h. It strikes the ground and does not rebound. The velocity of A relative to B versus time graph is best represented by (upward direction is positive). View SolutionQuestion 24
Two particles are projected simultaneously from the same point, with the same speed, in the same vertical plane, and at different angles with the horizontal in a uniform gravitational field acting vertically downwards. A frame of reference is fixed to one particle. The position vector of the other particle , as observed from this frame, is →r. Which of the following statement is correct? View SolutionQuestion 28
Two particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]
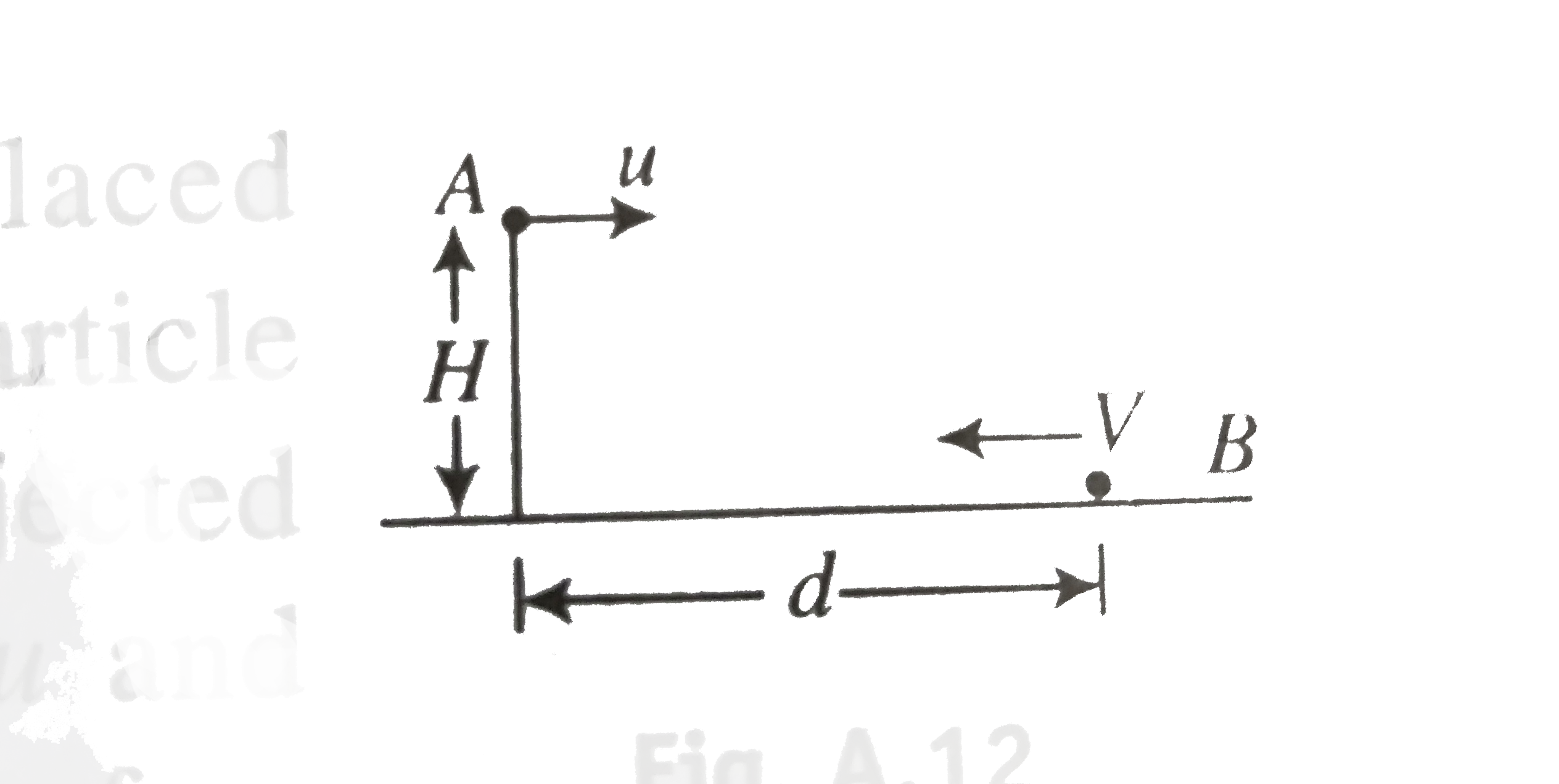 View Solution
View SolutionQuestion 35
Shots are fired simultaneously from the top and bottom of a vertical cliff with the elevation α=30∘, beta =60∘, respectively. The shots strike an object simultaneously at the same point. If a=10(√3) m is the horizontal distance of the object from the cliff, then the height h of the cliff is
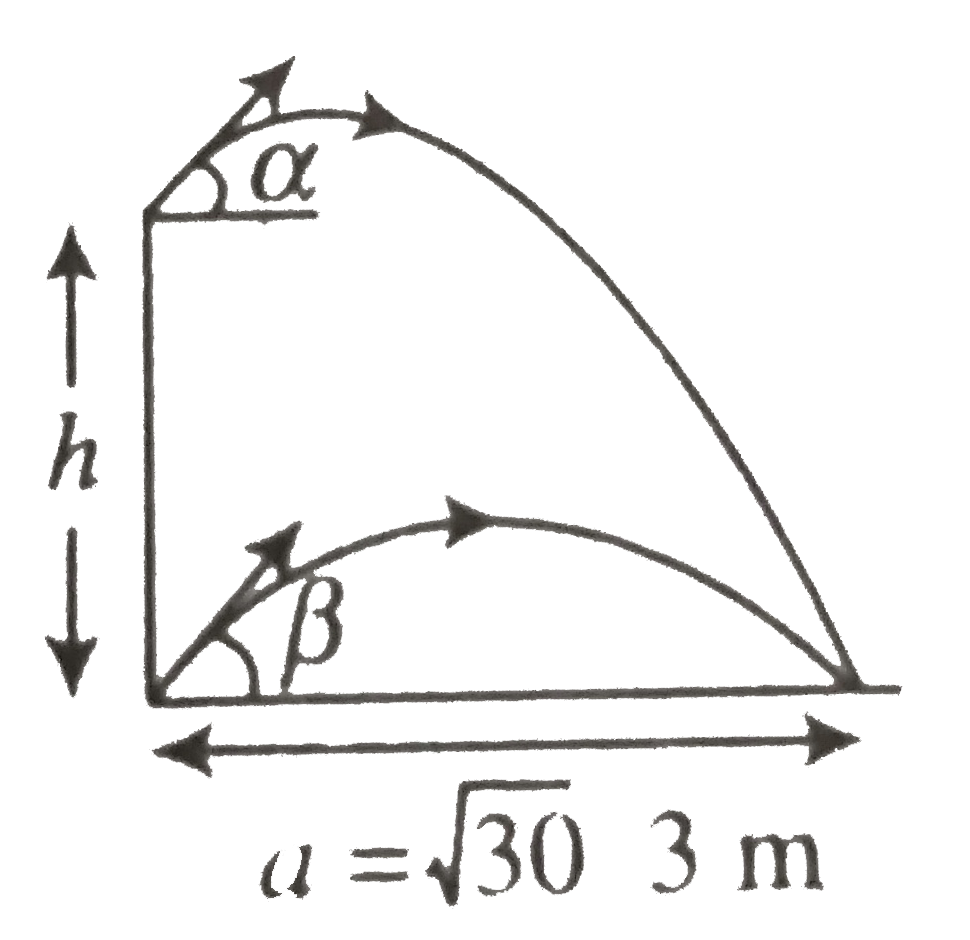 View Solution
View SolutionQuestion 42
Figure shows path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram can not be true in any situation? (In each figure velocity is tangential to the trajectory).
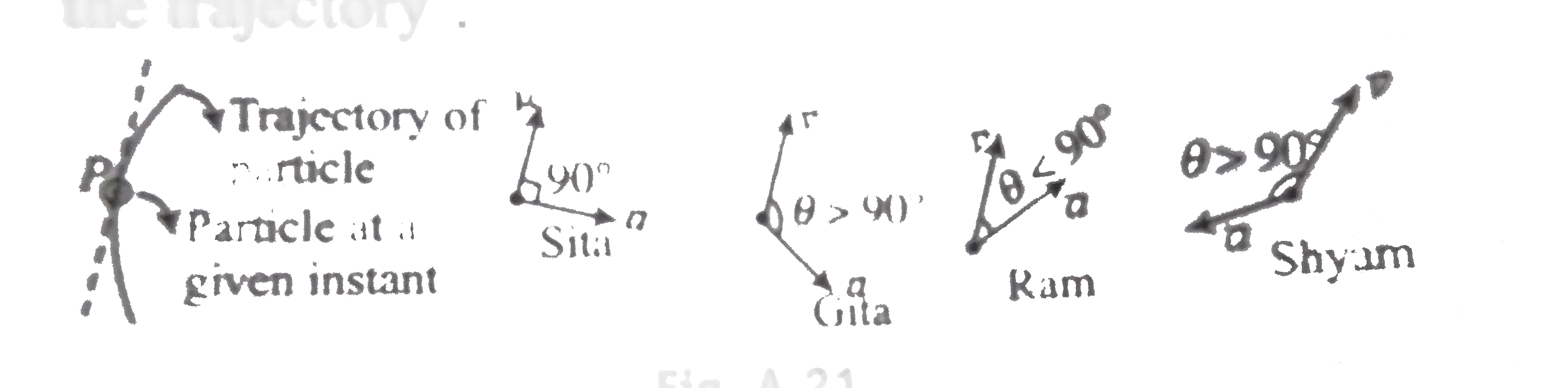 View Solution
View SolutionQuestion 46
Two identical balls are set into motion simultaneously from an equal height h. While ball A is thrown horizontally with velocity v, ball B is just released to fall by itself. Choose the alternative that best represents the motion of A and B with respect to an observer who moves with velocity v/2 with respect to the ground as shown in the figure.
 View Solution
View SolutionQuestion 47
An aeroplane is flying vertically upwards. When it is at a height of 1000m above the ground and moving at a speed of 367m/s., a shot is fired at it with a speed of 567 ms−1 from a point directly below it. What should be the acceleration of aeroplane so that it may escape from being hit? View SolutionQuestion 50
A man is riding on a horse. He is trying to jump the gap between two symmetrical ramps of snow separated by a distance W as shown in figure. He launches off the first ramp with a speed vL. The man and the horse have a total mass m. and their size is small as compared to W. The value of initial launch speed VL which will put the horse exactly at the peak of the second ramp is
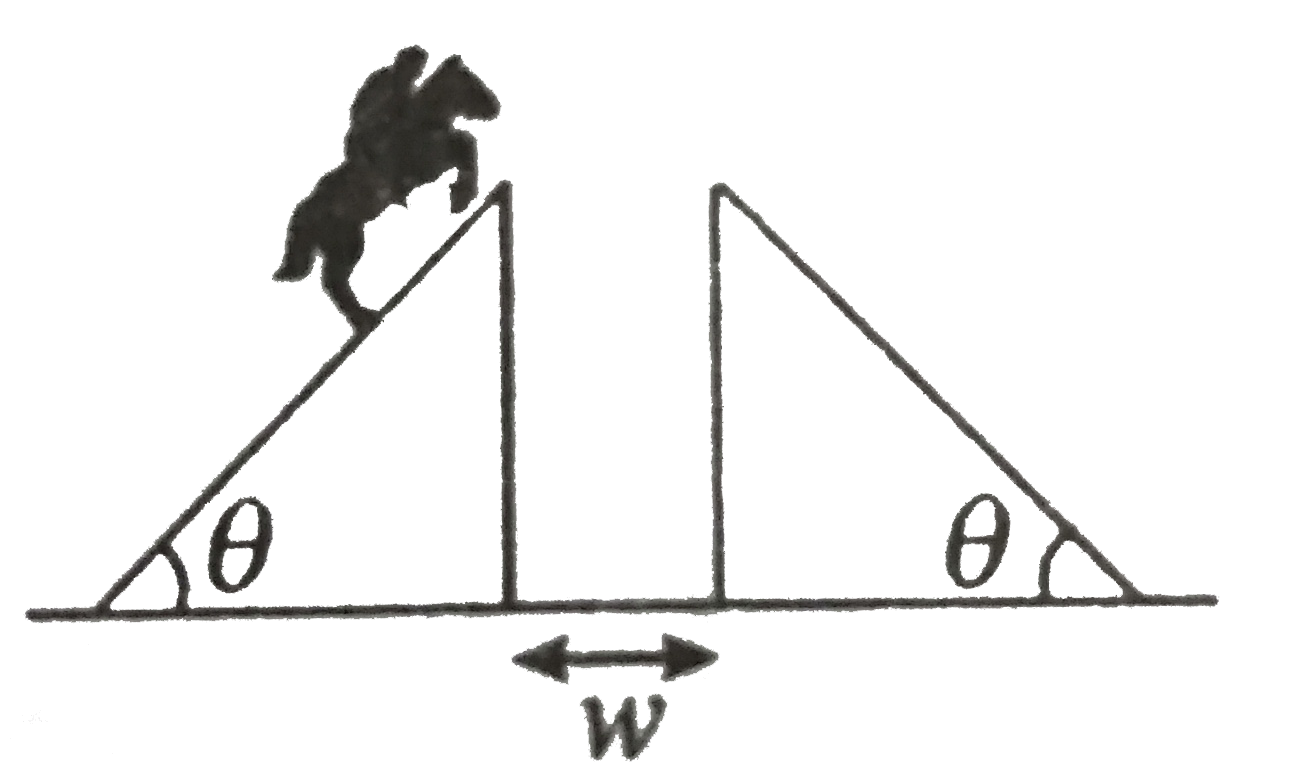 View Solution
View SolutionQuestion 70
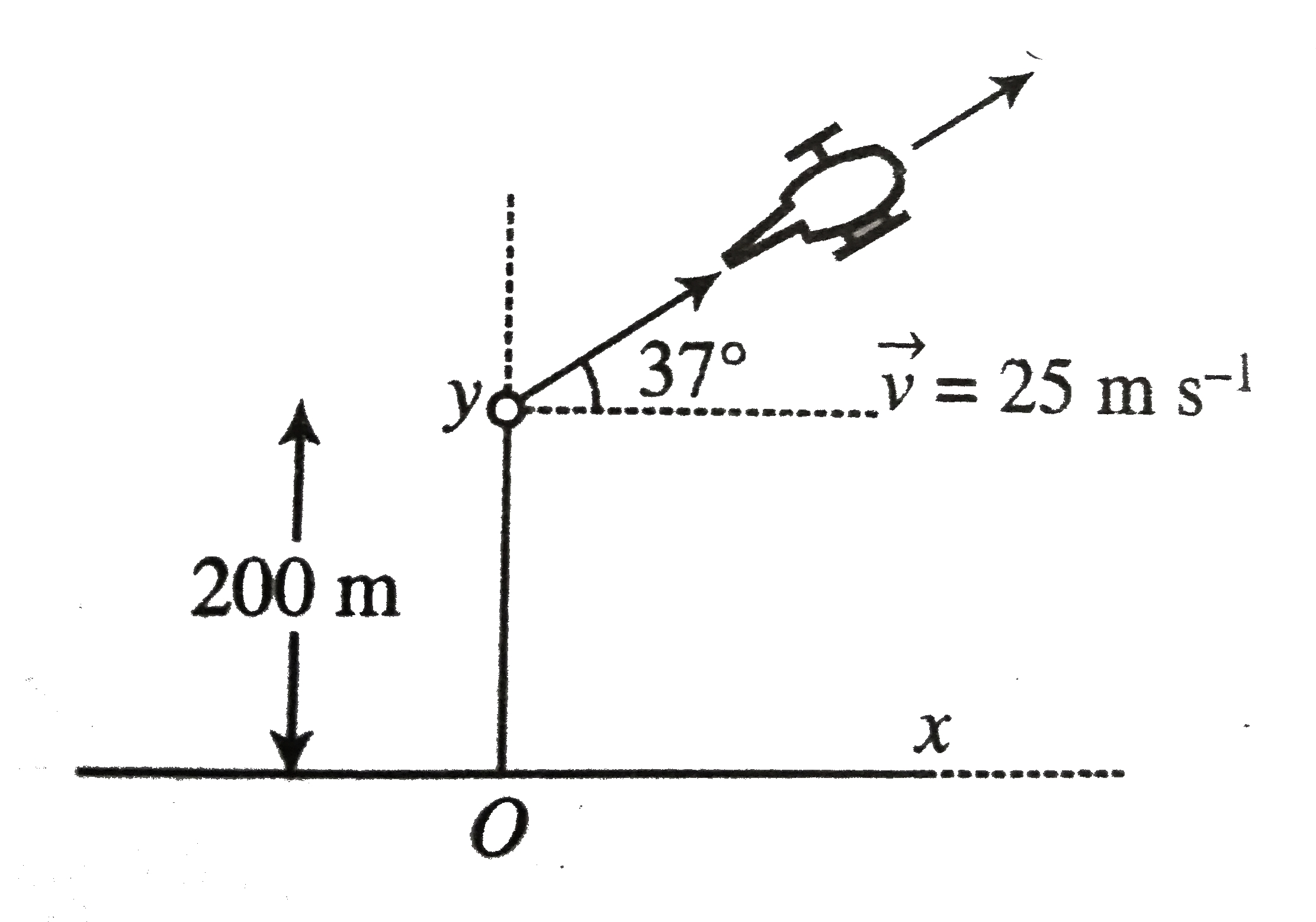
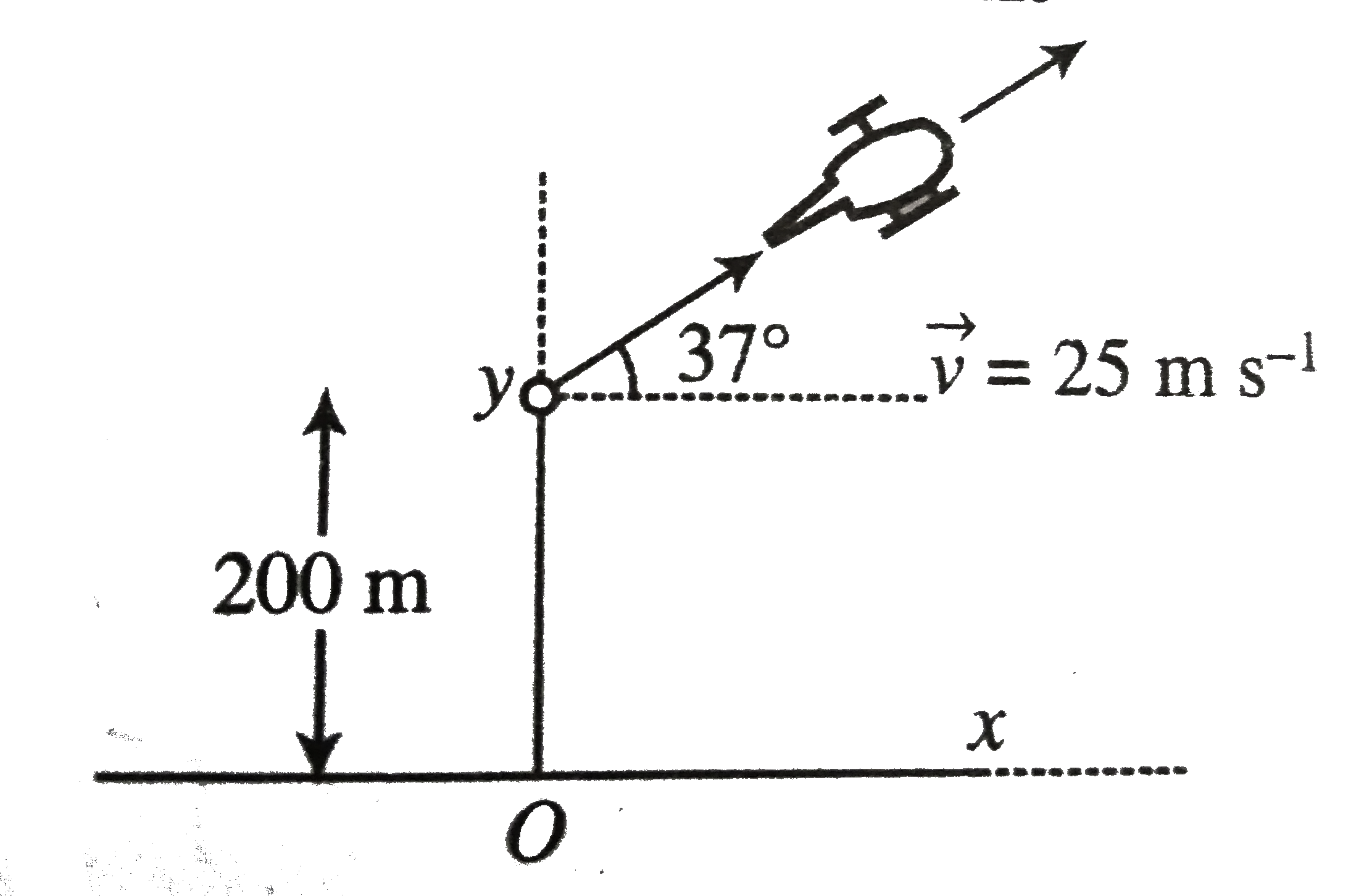
Consider a shell that has a muzzle velocity of 45ms−1 fired from the tail gun of an airplane moving horizontally with a velocity of 215ms−1 . The tail gun can be directed at any angle with the vertical in the plane of motion of the airplane. The shell is fired when the plane is above point A on ground, and the plane is above point B on ground when the shell hits the ground. (Assume for simplicity that the Earth is flat)View SolutionQuestion 74
A cubical box dimension L=5/4 m starts moving with an acceleration →a=0.5ms−2ˆi form the state of rest. At the same time, a stone is thrown form the origin with velocity →V=v1ˆi+v2ˆj−v3ˆk with respect to earth. Acceleration due to gravity →g=10ms−2(−ˆj). The stone just touches the roof of box and finally falls at the diagonally opposite point. then: View SolutionQuestion 75
An inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00 (hh:mm:ss:100 th part of the second). Find the value of g. (correct upt ot two decimal places). View SolutionQuestion 76
An inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00. What should be the initial downward speed of the rocketeer so that he catches the student at the top of 100 the floor for safe landing ? View SolutionQuestion 77
An inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
The correct velocity - time graph for the rocketeer would be View SolutionQuestion 78
An inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
In Q.1, what would be the approximate retardation to be given by jet pack along for safe landing? View SolutionQuestion 79
An inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
The correct velocity - time graph for the rocketeer would be View SolutionQuestion 80
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
1. The time in which the ball strikes the floor of elevator is given byView SolutionQuestion 81
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
2. The maximum height reached by ball, as measured from the ground would beView SolutionQuestion 82
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
3. Displacement of ball with respect to ground during its night would beView SolutionQuestion 83
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
3. Displacement of ball with respect to ground during its night would beView SolutionQuestion 84
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
4. The maximum separation between the floor of elevator and the ball during its flight would beView SolutionQuestion 85
Projectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘<θ<180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A particle is projected from the origin in the x-y plane. The acceleration of particle in negative y-direction is α. If equation of path of the particle is y=ax−bx2, then initial velocity of the particle is View SolutionQuestion 86
Projectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘ltθlt180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
An object is projected from origin in x-y plane in which velocity changes according to relation →v=aˆi+bxˆj. Path of particle is View SolutionQuestion 87
Projectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘<θ<180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A body is projected at angle of 30∘ and 60∘ with the same velocity. Their horizontal ranges are R1 and R2 and maximum heights are H1andH2, respectively, then
A body is projected at angle of 30∘ and 60∘ with the same velocity. Their horizontal ranges are R1 and R2 and maximum heights are H1 and H2, respectively, then View SolutionQuestion 93
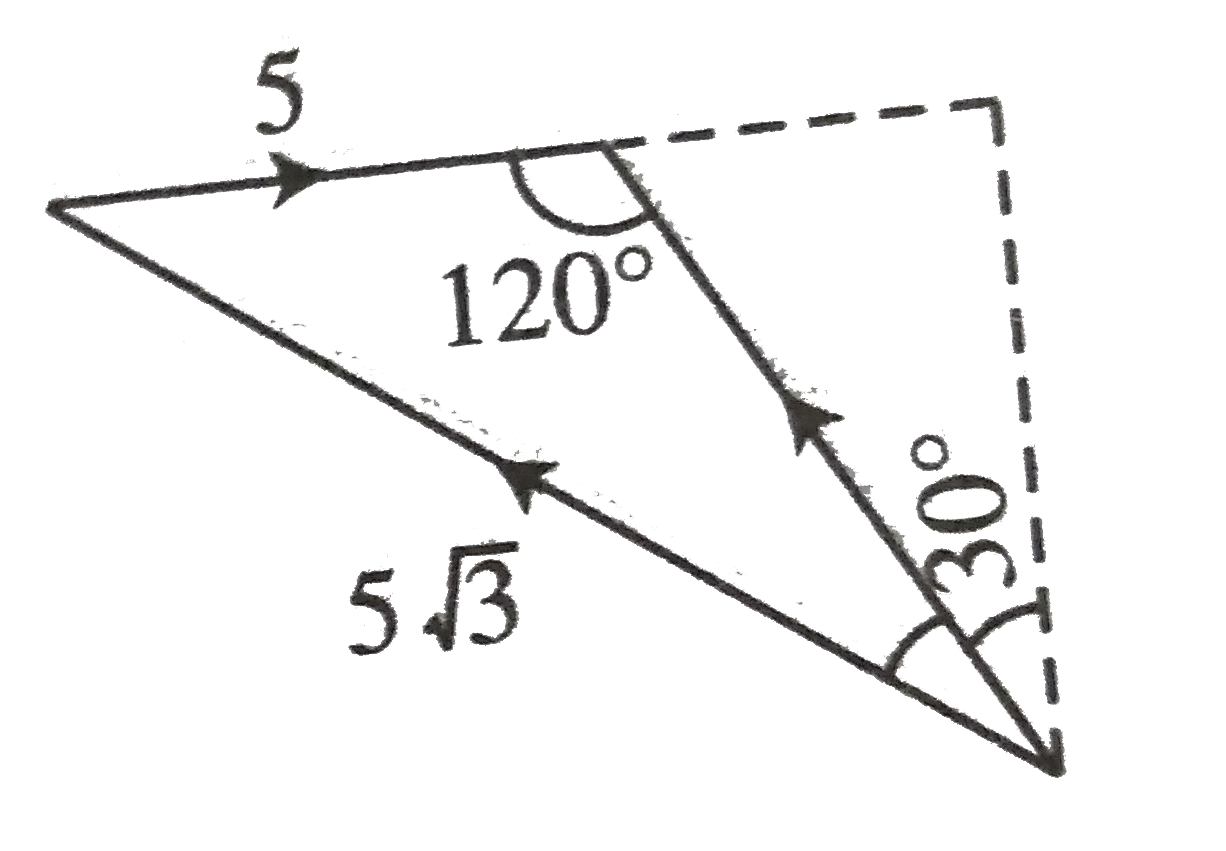
Two inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10(√3)ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
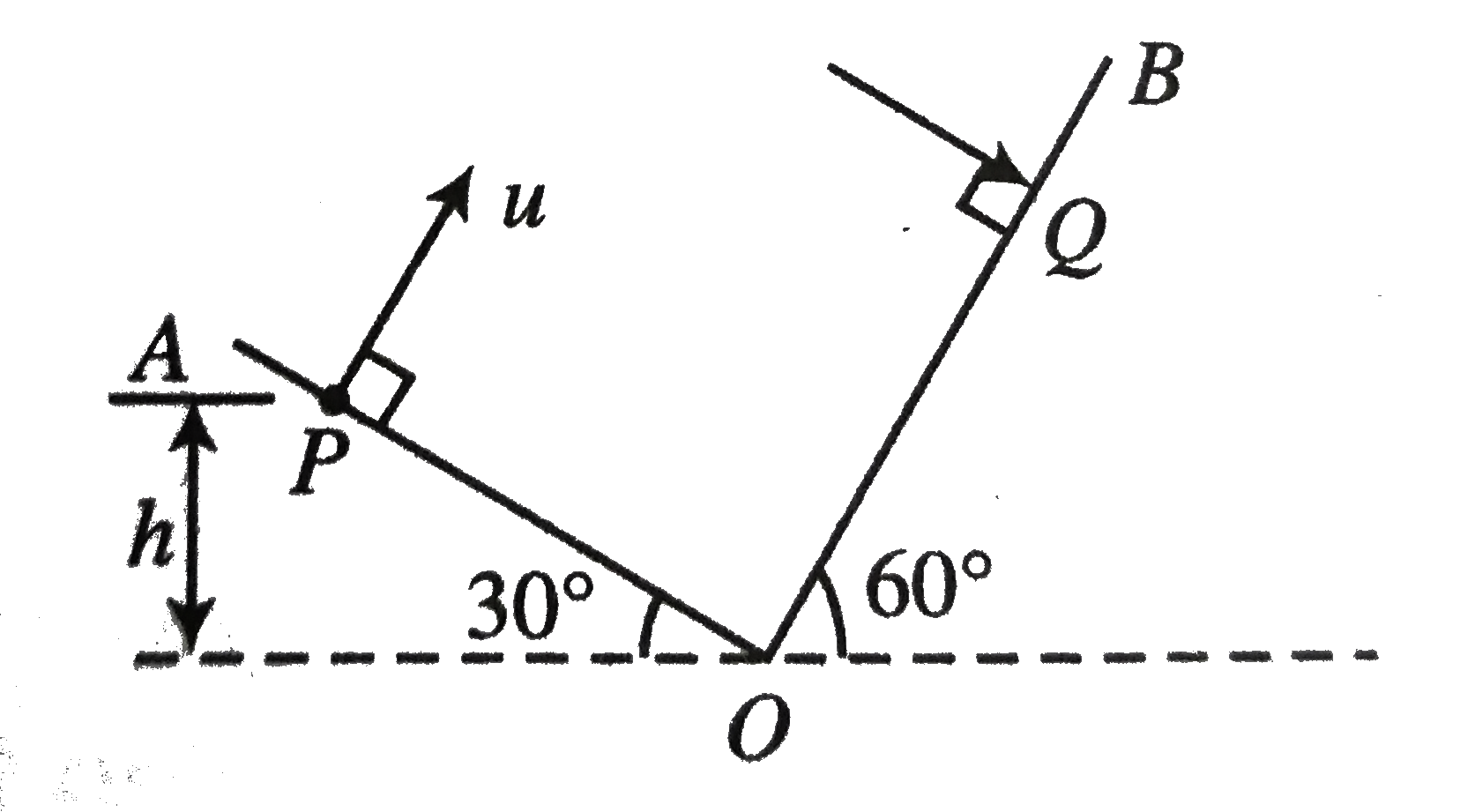
The velocity with which particle strikes the plane OB, View SolutionQuestion 94
Two inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10(√3)ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate

The velocity with which particle strikes the plane OB, View SolutionQuestion 95
Two inclined planes OA and OB having inclination (with horizontal) 30∘and60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
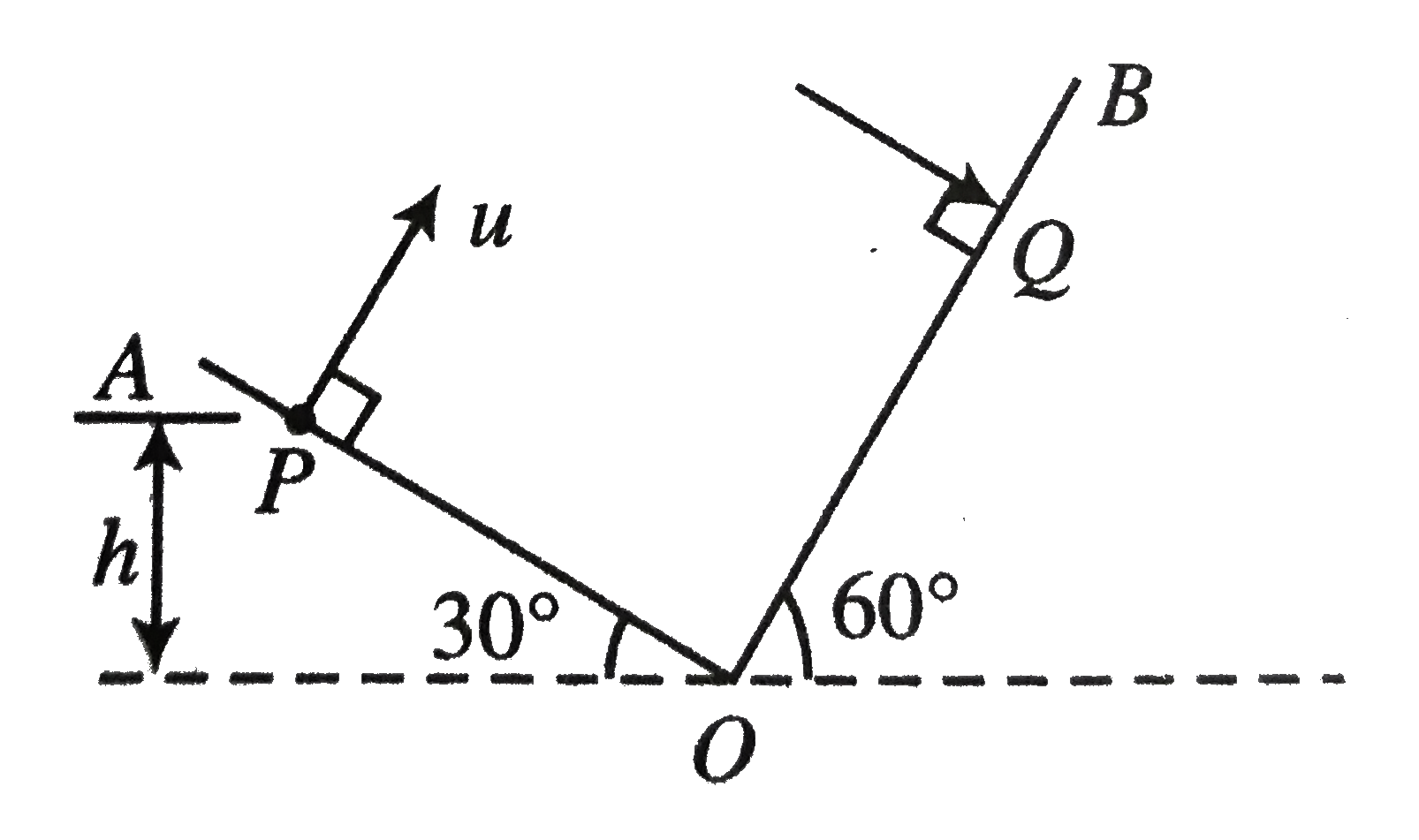
The vertical height h of P from O, View SolutionQuestion 96
Two inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘(with horizontal), respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
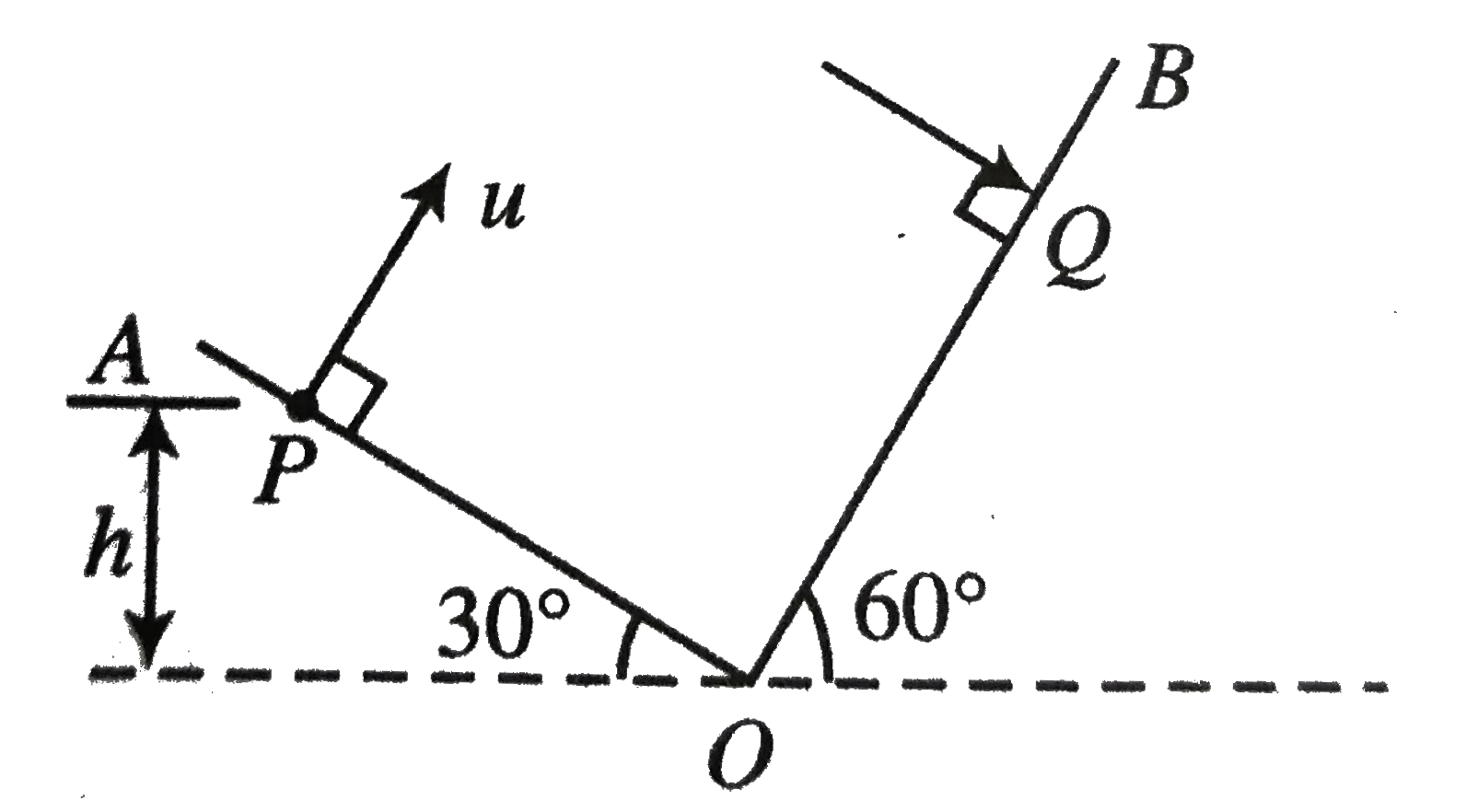
The maximum height attained by the particle (from the line O)View SolutionQuestion 97
Two inclined planes OA and OB having inclinations 30∘ and 60∘ with the horizontal respectively intersect each other at O, as shown in figure. A particle is projected from point P with velocity u=10√3m/s along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q. Calculate.
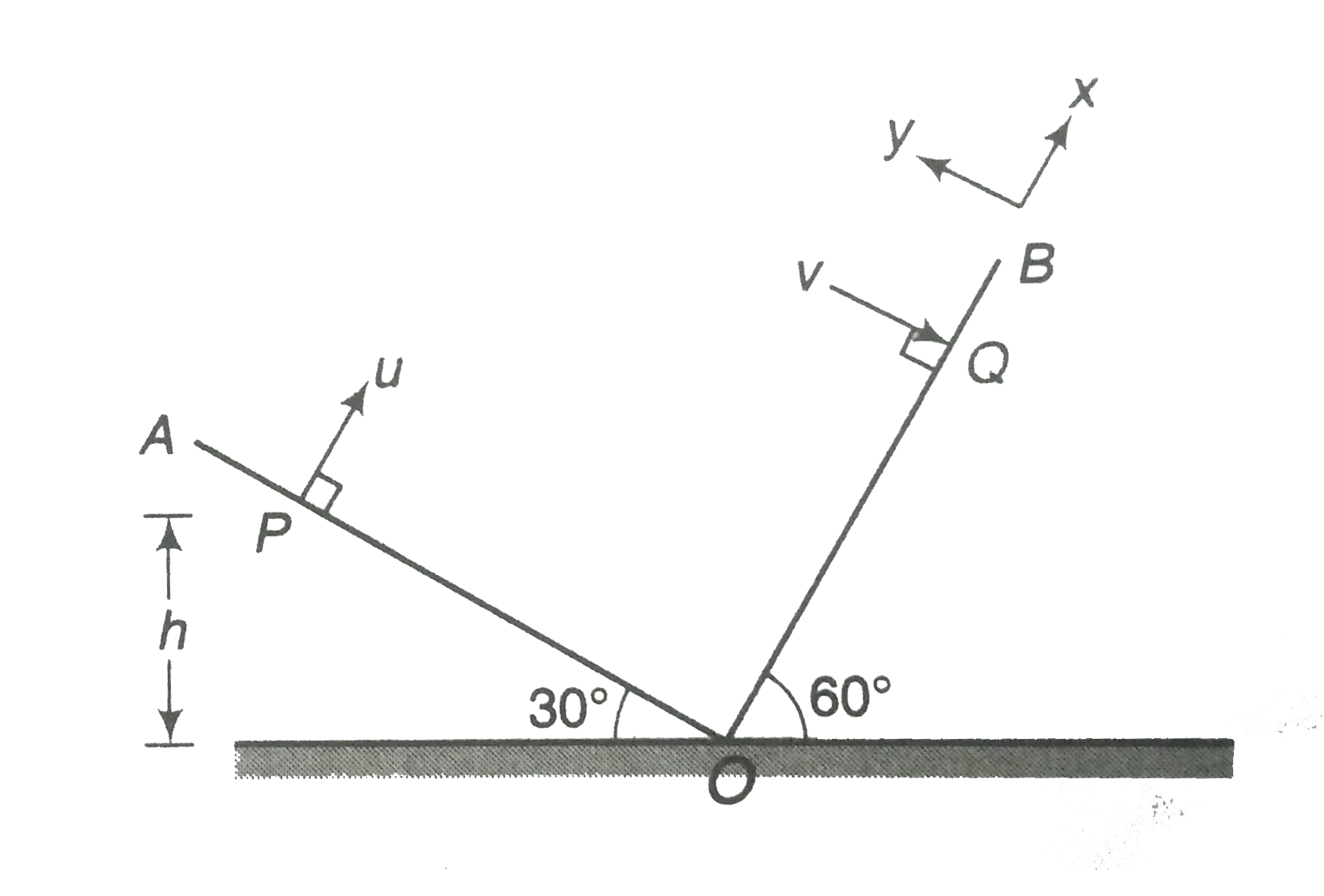
(a) time of flight,
(b) velocity with which the particle strikes the plane OB,
(c) height h of point P from point O,
(d) distance PQ. (Take g=10m/s2)View SolutionQuestion 101
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
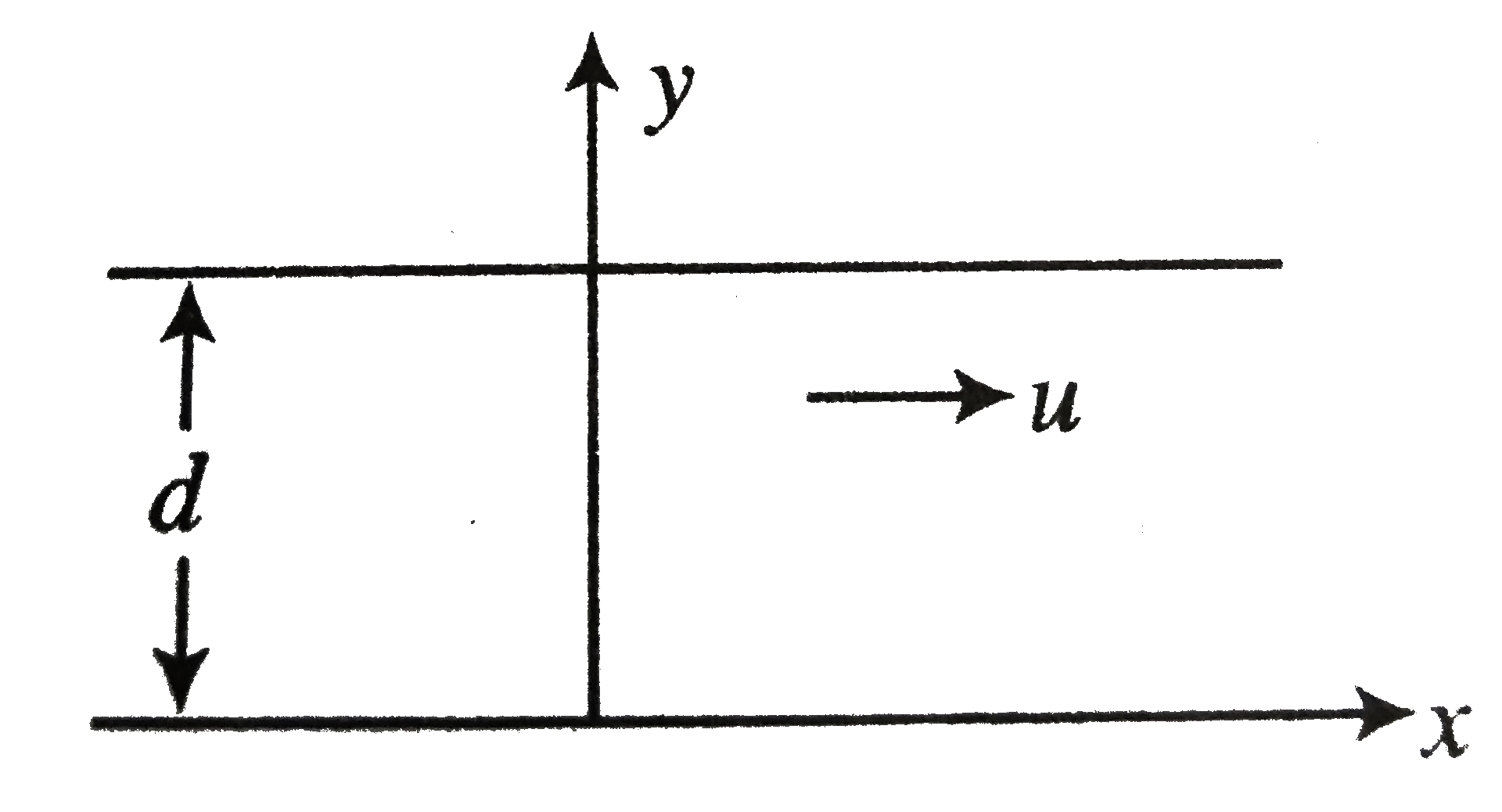
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.View SolutionQuestion 102
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
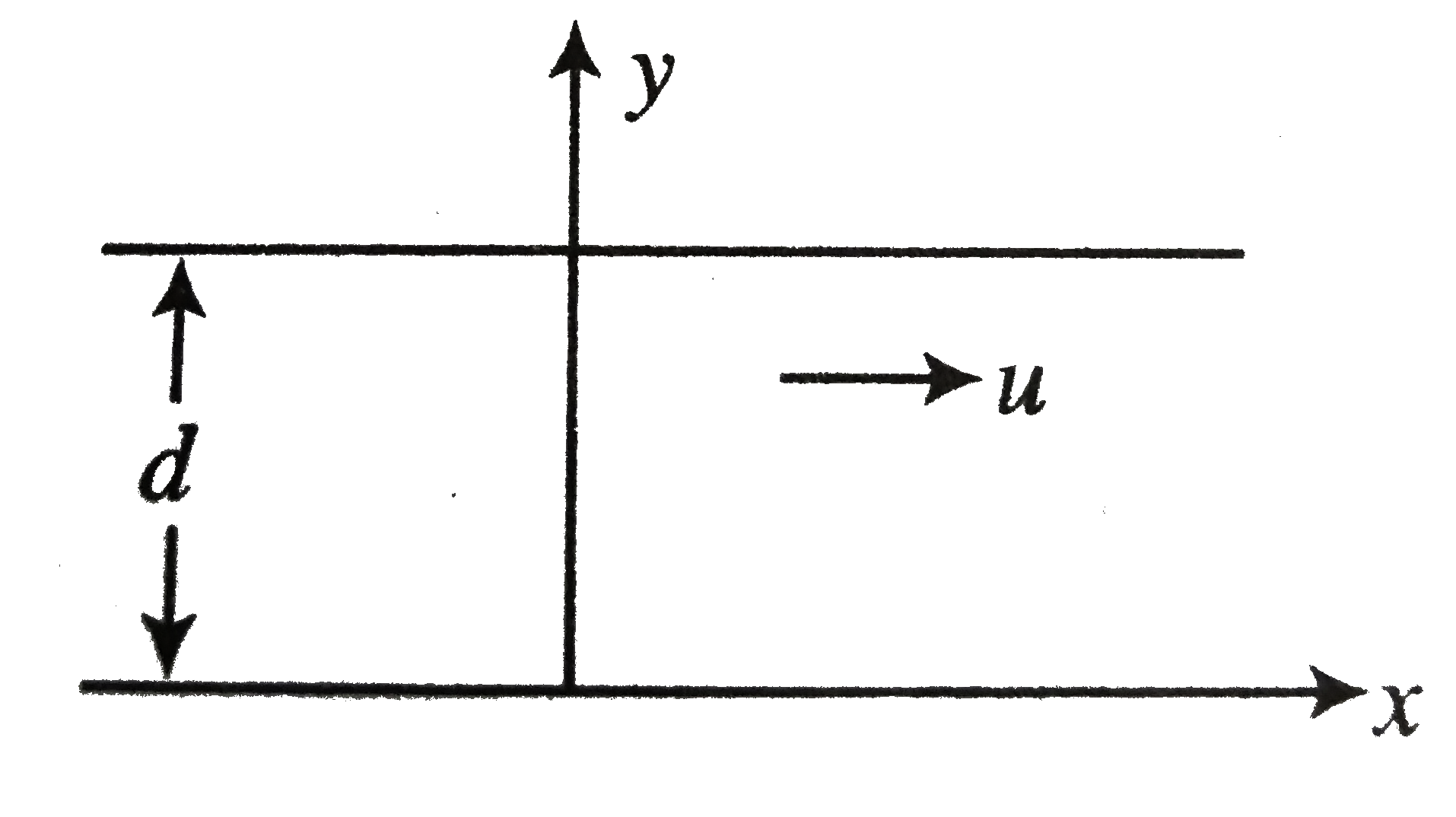
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. View SolutionQuestion 103
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. View SolutionQuestion 104
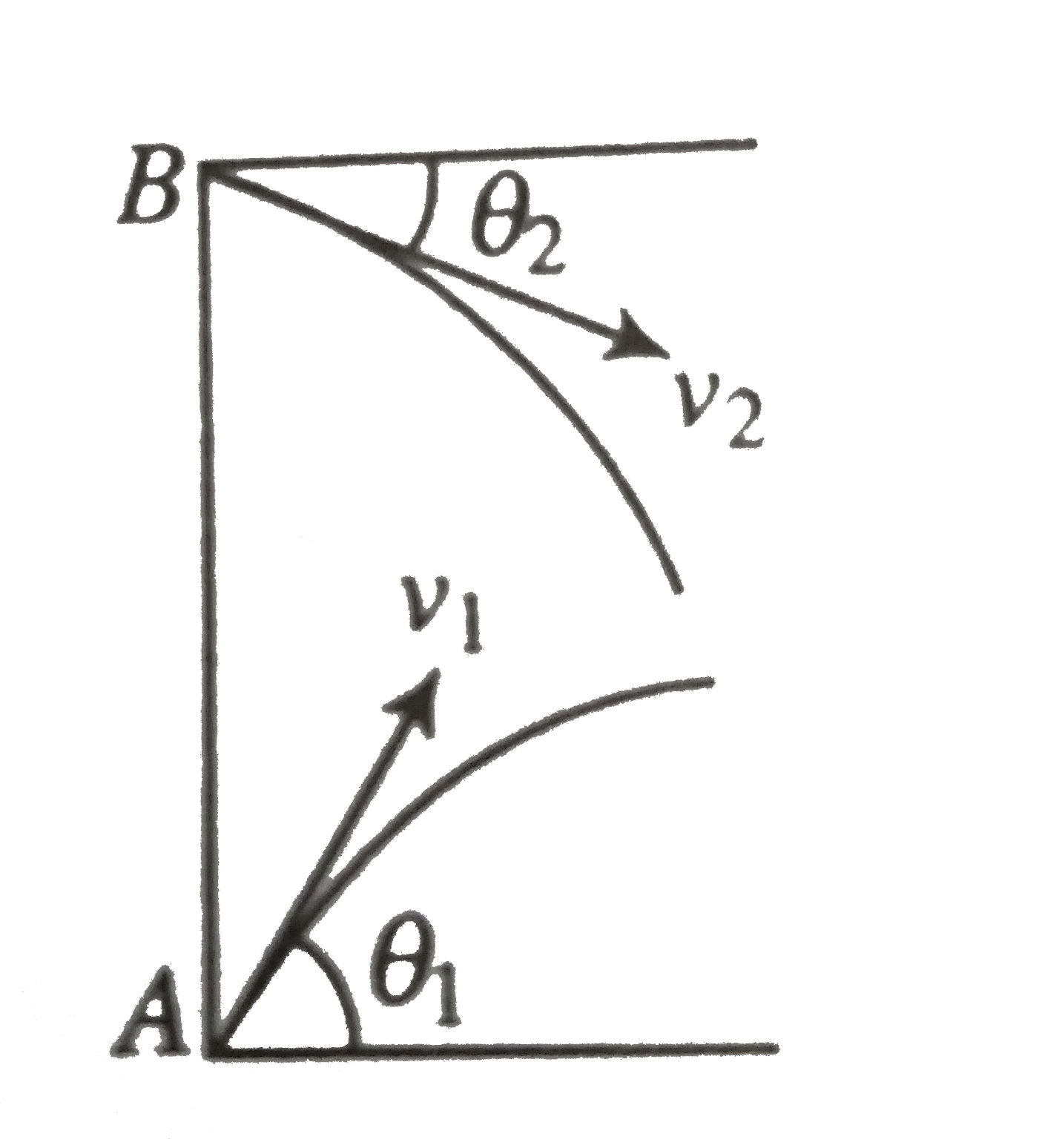
Ram Shyam are walking on two perpendicular tracks with speed 3ms−1 and 4ms−1, respectively. At a certain moment (sayt=0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
During the motion the magnitude of velocity of ram with respect to Shyam is View SolutionQuestion 105
Ram Shyam are walking on two perpendicular tracks with speed 3ms−1 and 4ms−1, respectively. At a certain moment (t=0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
During the motion the magnitude of velocity of ram with respect to Shyam is View SolutionQuestion 106
Ram Shyam are walking on two perpendicular tracks with speed 3ms−1and4ms−1, respectively. At a certain moment (say t = 0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
The time t when they are at shortest distance from each other subsequently is - View SolutionQuestion 110
In a square cut, the speed of the cricket ball changes from 30ms−1 to 40ms−1 during the time of its contact Δt=0.01s with the bat. If the ball is deflected by the bat through an angle of θ=90∘, find the magnitude of the average acceleration (in×102ms−2) of the ball during the square cut. View SolutionQuestion 112
Two bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10m and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
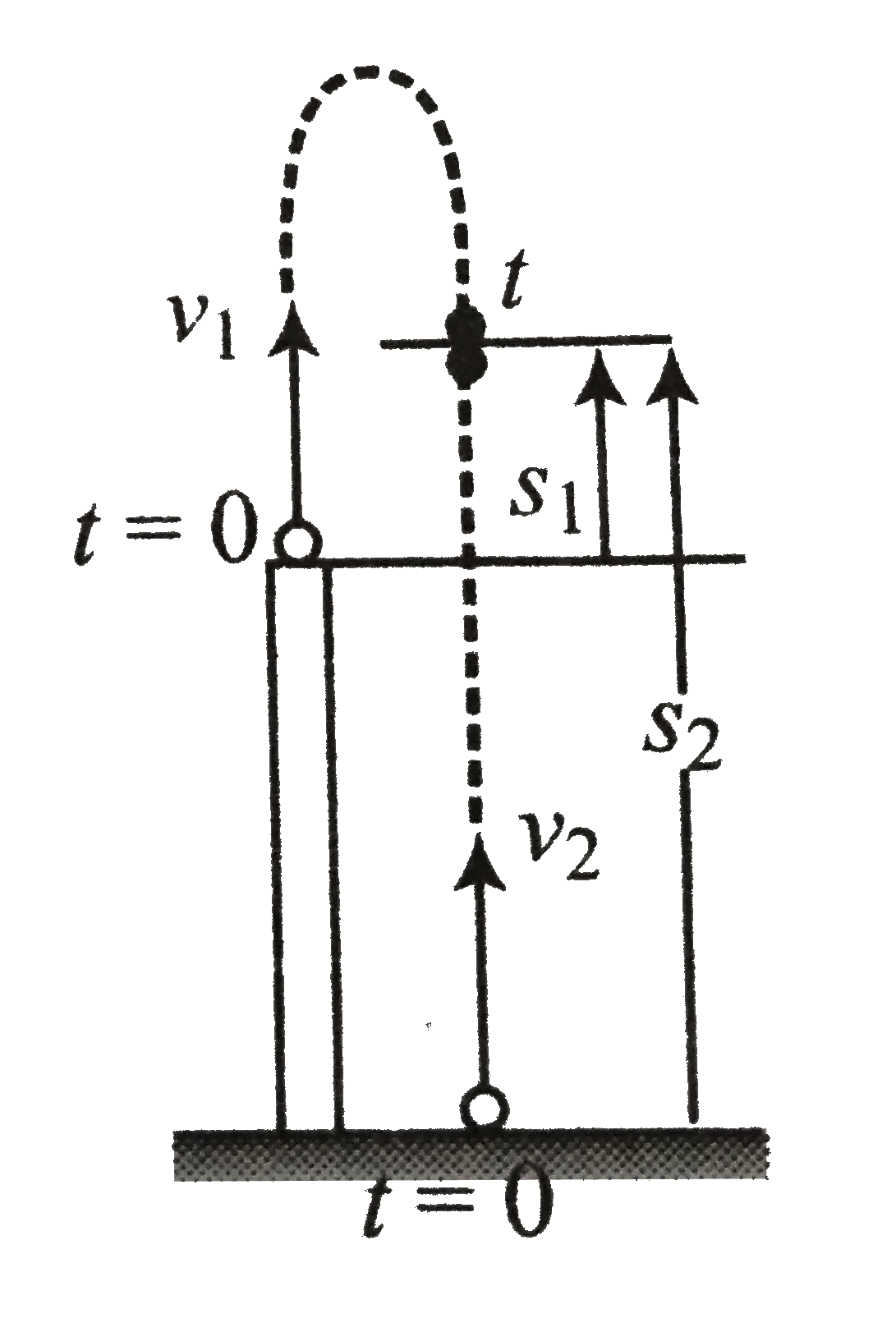 View Solution
View SolutionQuestion 119
A projectile is launched at time t = 0 from point A which is at height 1 m above the floor with speed vms−1 and at and angle θ=45∘ with the floor. It passes through a hoop at B which is 1 m above A and B is the highest point of the trajectory. The horizontal distance between A and B is d meters. The projectile then falls into a basket, hitting the floor at C a horizontal distance 3 d meters from A. Find l (in m).
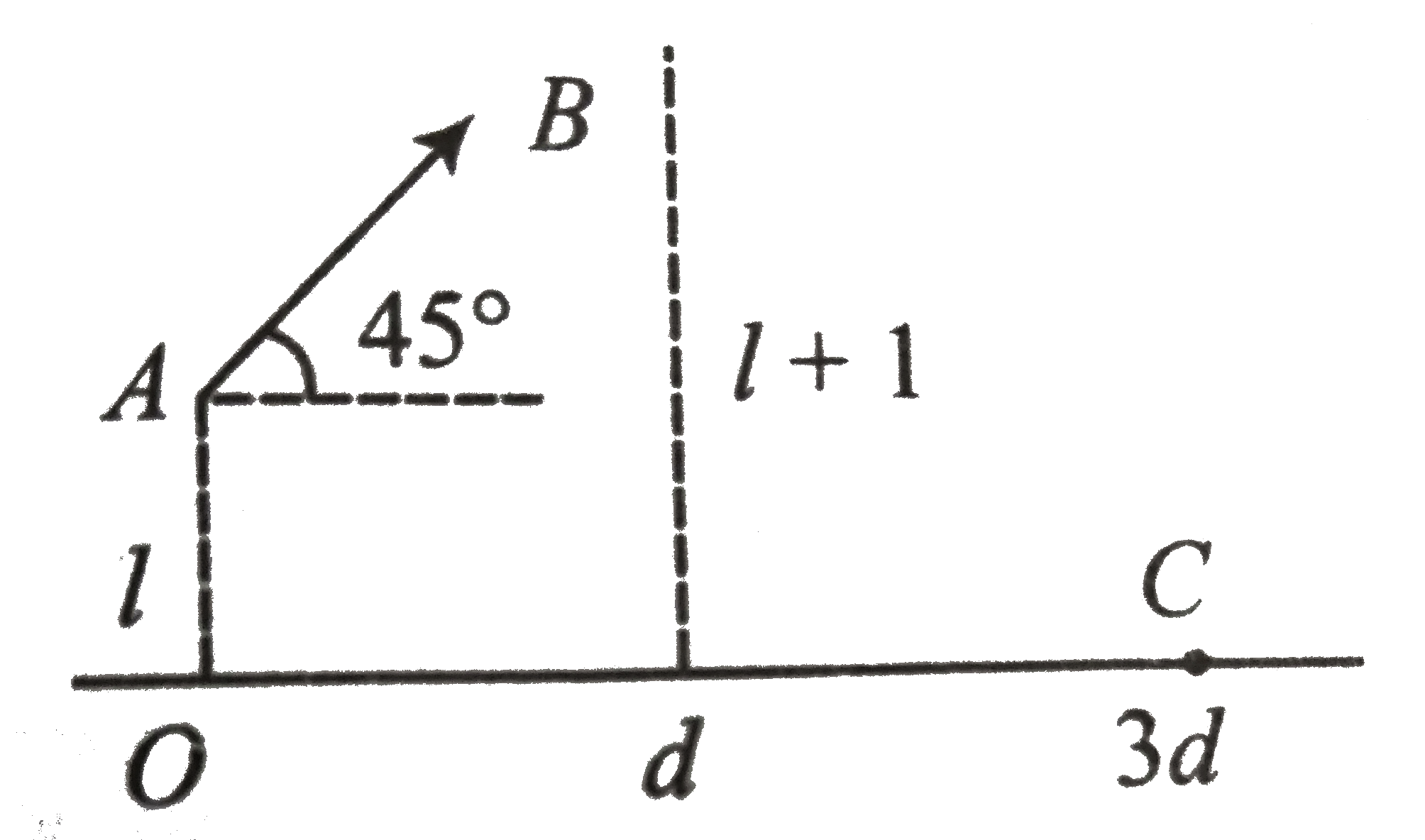 View Solution
View SolutionQuestion 122
Figure shows a method for measuring the acceleration due to gravity. The ball is projected upward by a gun. The ball pases the electronic gates 1 and 2 as it rises and again as it falls. Each gate is connected to a separate timer. The first passage of the ball through each gate stars the corresponding timer, and the second passage through the same gate stops the timer. the time intervals △t1 and △t2 are thus measured. The vertical distance between the two gates is d. If d=5m,△t1=3s,△t2=2s, then find the measured value of acceleration due to gravity (in m/s2)
 View Solution
View SolutionQuestion 124
A big Diwali rocket is projected vertically upward so as to attain a maximum height of 160 m. The rocket explodes just as it reaches the top of its trajectory sending out luminous particles in all possible directions all with same speed v. The display, consisting of the luminous particles, spreads out as an expanding, brilliant sphere. The bottom of this sphere just touches the ground when its radius is 80 m. With what speed (inm/s)are the luminous particles ejected by the explosion? View SolutionQuestion 125
A student throws soft balls out of the window at different angles to the horizontal. All soft balls have the same initial speed v=10√3ms−1. It turns out that all soft balls landing velocities make angles 30∘ or greater with the horizontal. Find the height h (in m) of the window above the ground. View SolutionQuestion 126
A rope is strecthed between two boats at rest. A sailor in the first boat pulls the rope with a constant force of 100N. First boat with the sailor has mass of 250kg. Whereas the mass of second boat is double of this mass. If the initial distance between the boats was 100m. The time taken for two boats to meet each other is (neglect water resistance between boats and water)
 View Solution
View SolutionQuestion 130
The trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.View SolutionQuestion 141
Consider a disc rotating in the horizontal plane with a constant angular speed ω about its center O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 1/8 rotation, (ii) their range is less than half the disc radius, and (iii) ω remains constant throughout. Then
1.png) View Solution
View SolutionQuestion 142
A particle of mass m moves on the x- axis as follows : it starts from rest at t=0, from the point x=0, and comes to rest at t=1 at the point x=1. No other information is available about its motion at intermediate times (0<t<1) . If α denotes the instantaneous accelartion of the particle , then : View SolutionQuestion 144
A train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60∘ to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is View SolutionQuestion 145
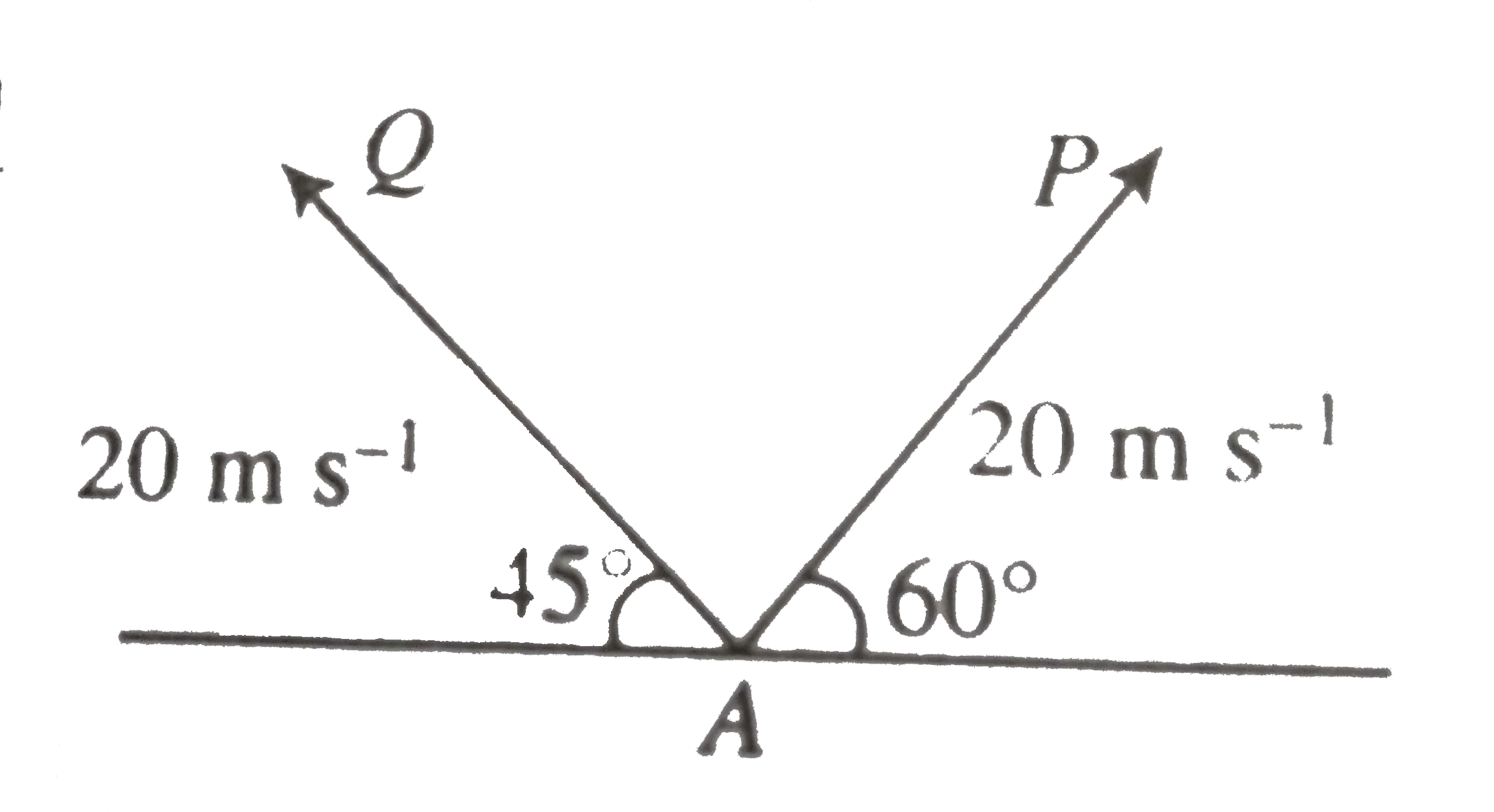
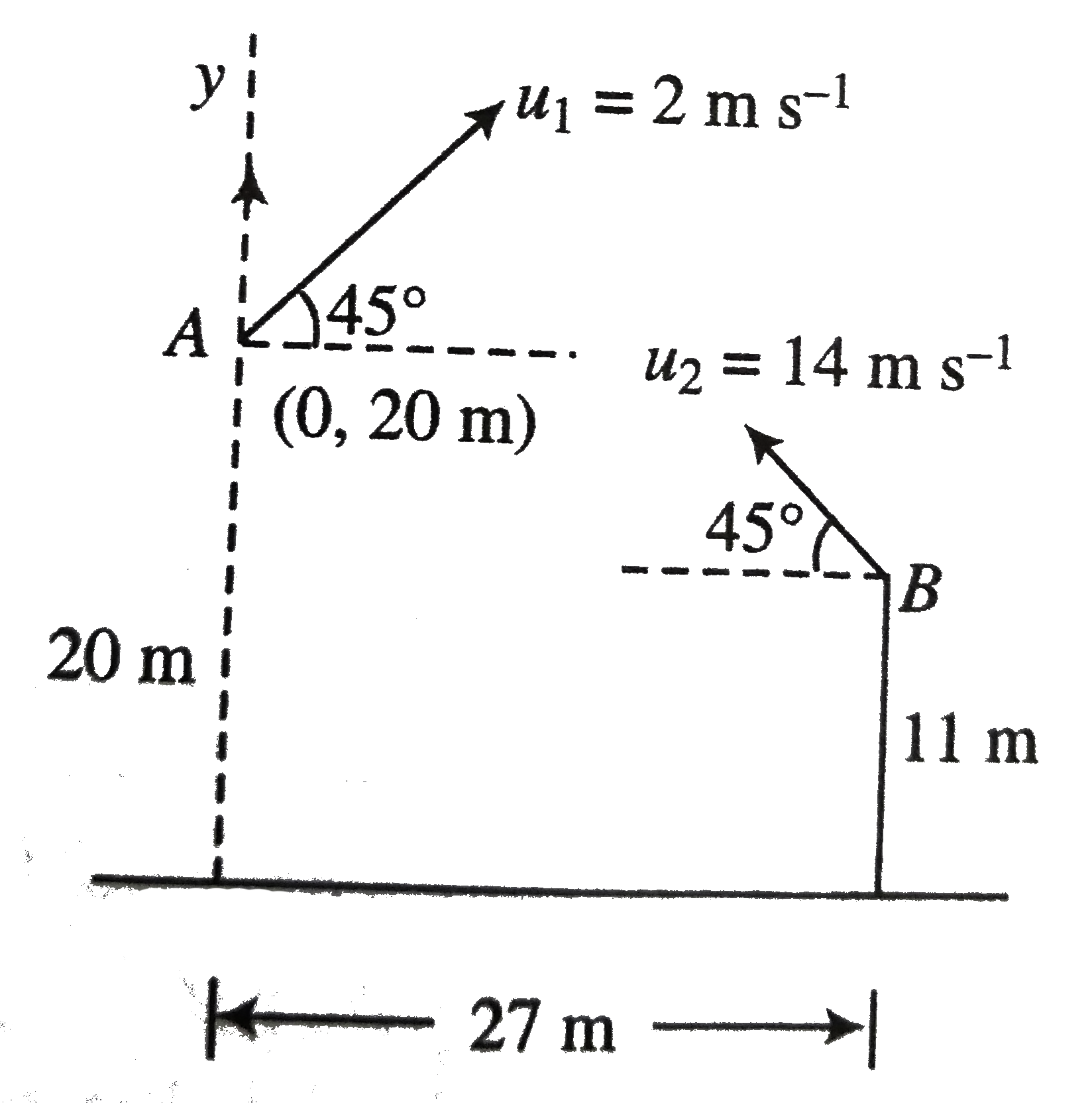
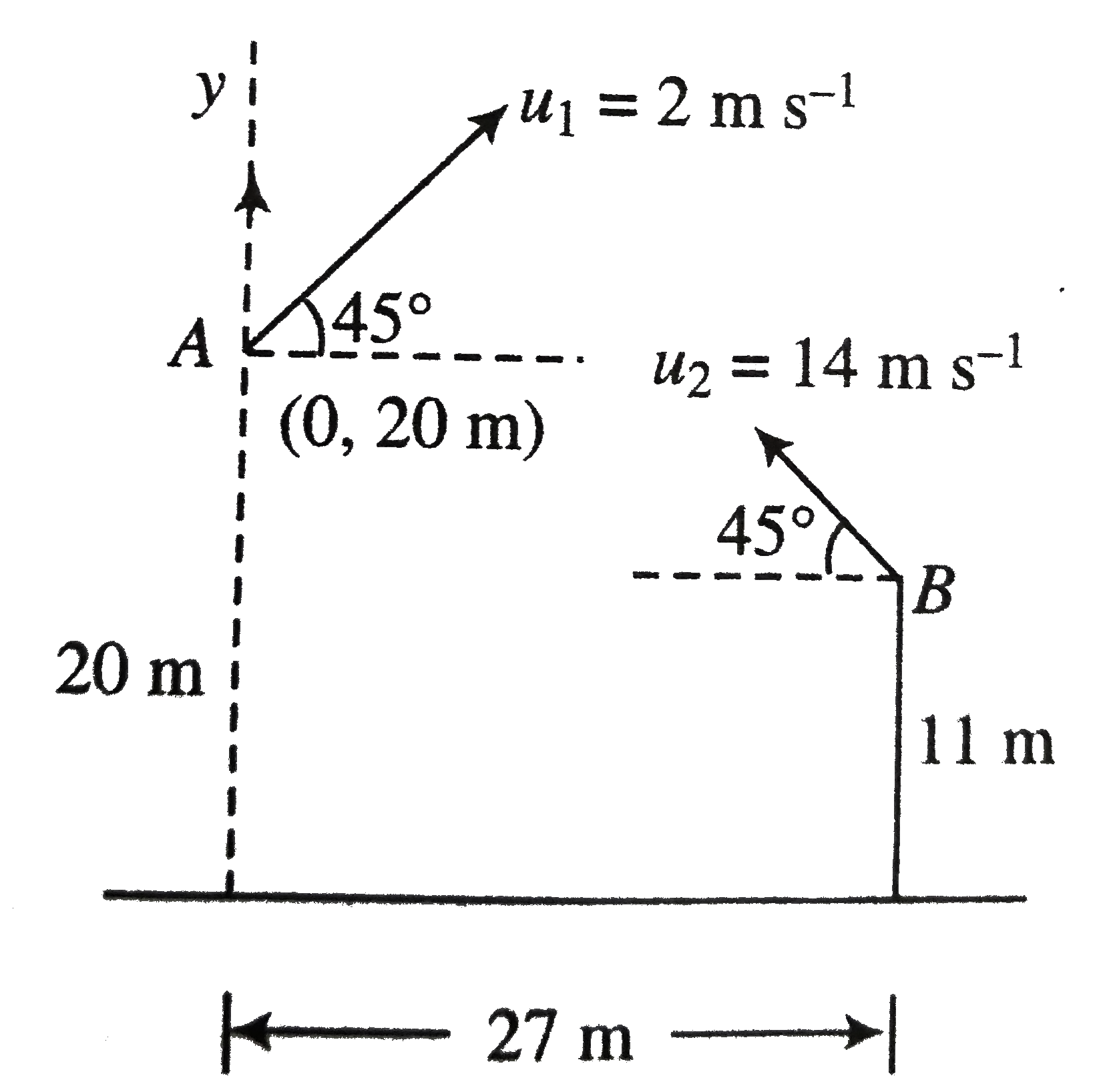
Airplanes A and B are flying with constant velocity in the same vertical plane at angles 30∘ and 60∘ with respect to the horizontal respectively as shown in figure . The speed of A is 100√3m/s . At time t=0s, an observer in A finds B at a distance of 500m. The observer sees B moving with a constant velocity perpendicular to the line of motion of A . If at t=t0, A just escapes being hit by B,t0 , A just escapes being hit by B,t0 in seconds is
 View Solution
View SolutionQuestion 146
A rocket is moving in a gravity free space with a constant acceleration of 2m/s2 along +x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3m/s relative to the rocket . At the same time , another ball is thrown in +x direction with a speed of 0.2m/s drom its right end relative to the rocket . The time in seconds when the two balls hit each other is
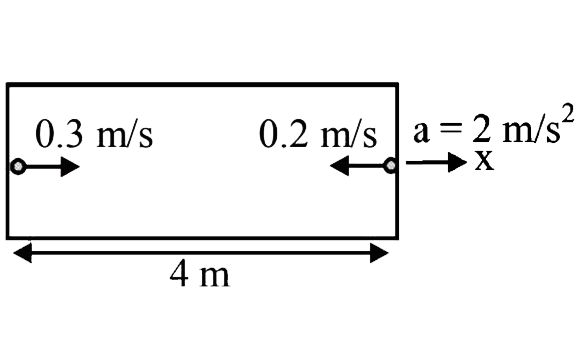 View Solution
View Solution

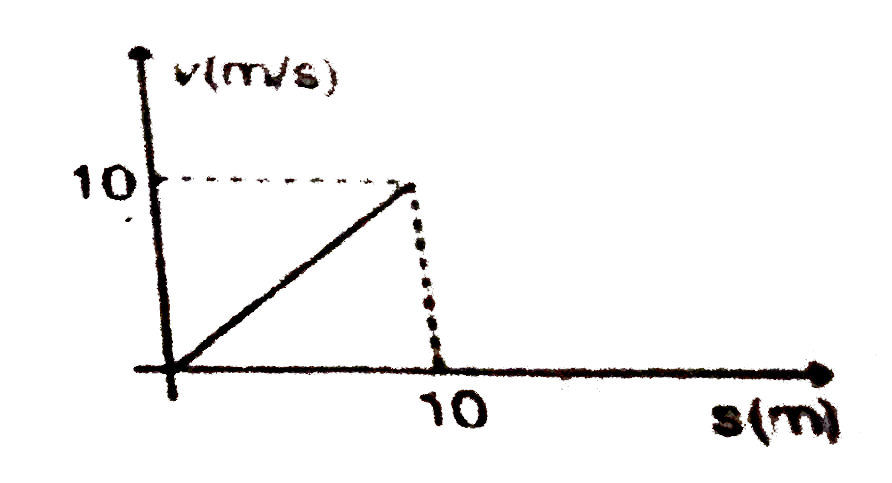
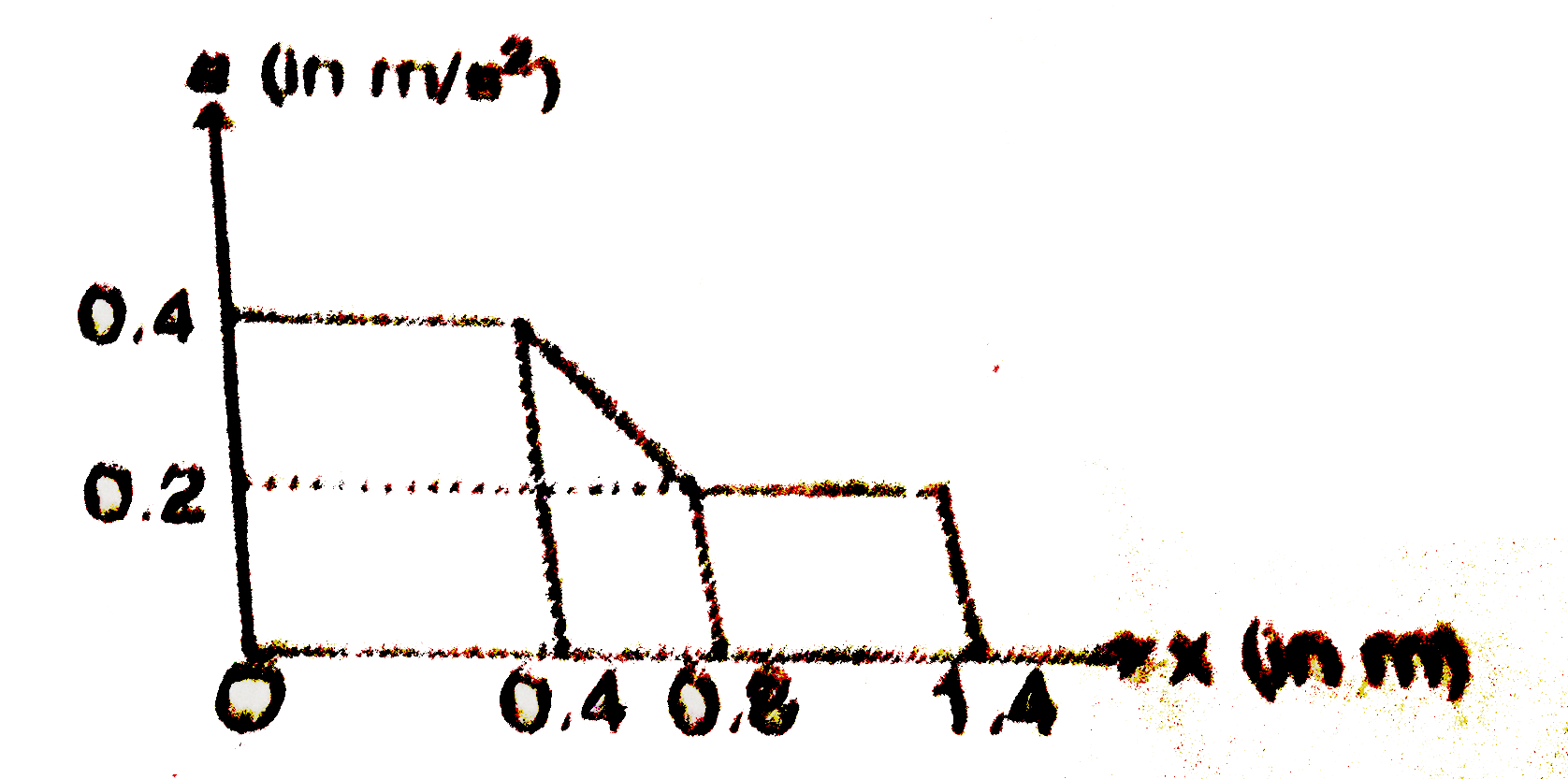
 .
. 
 .
. 
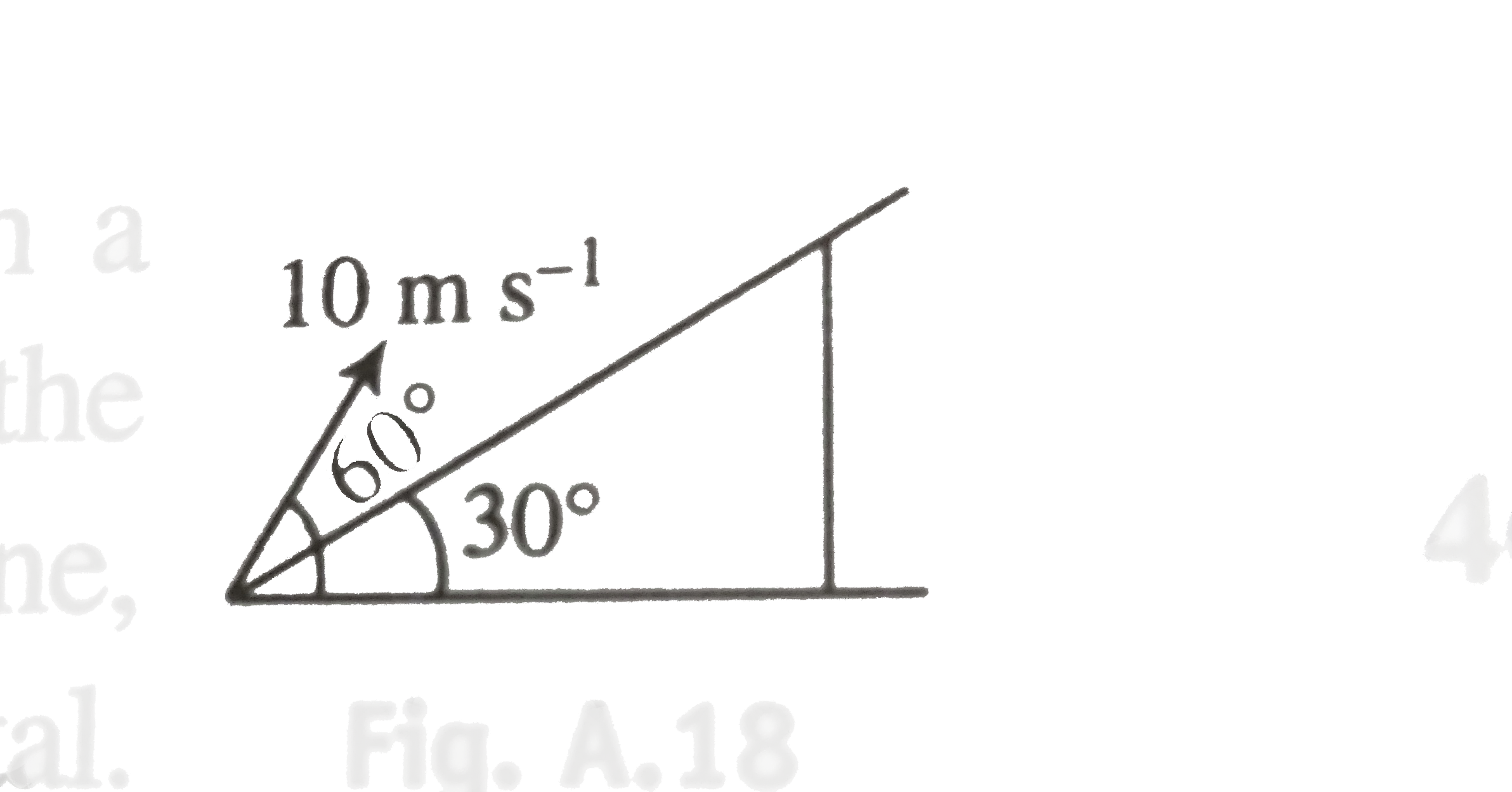
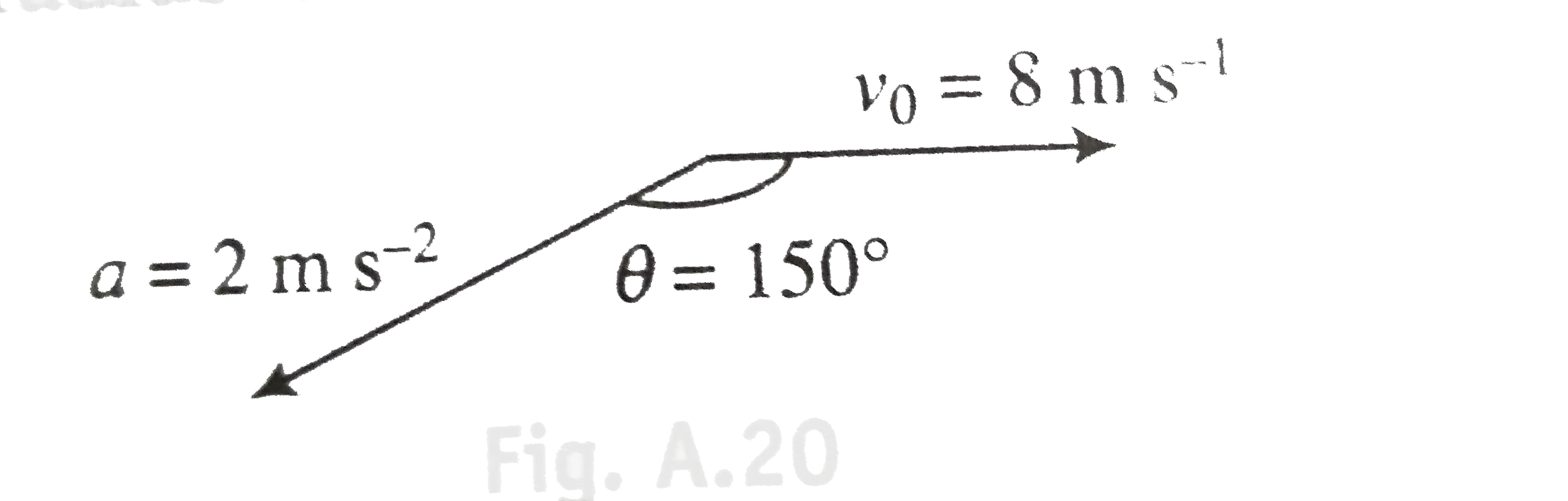


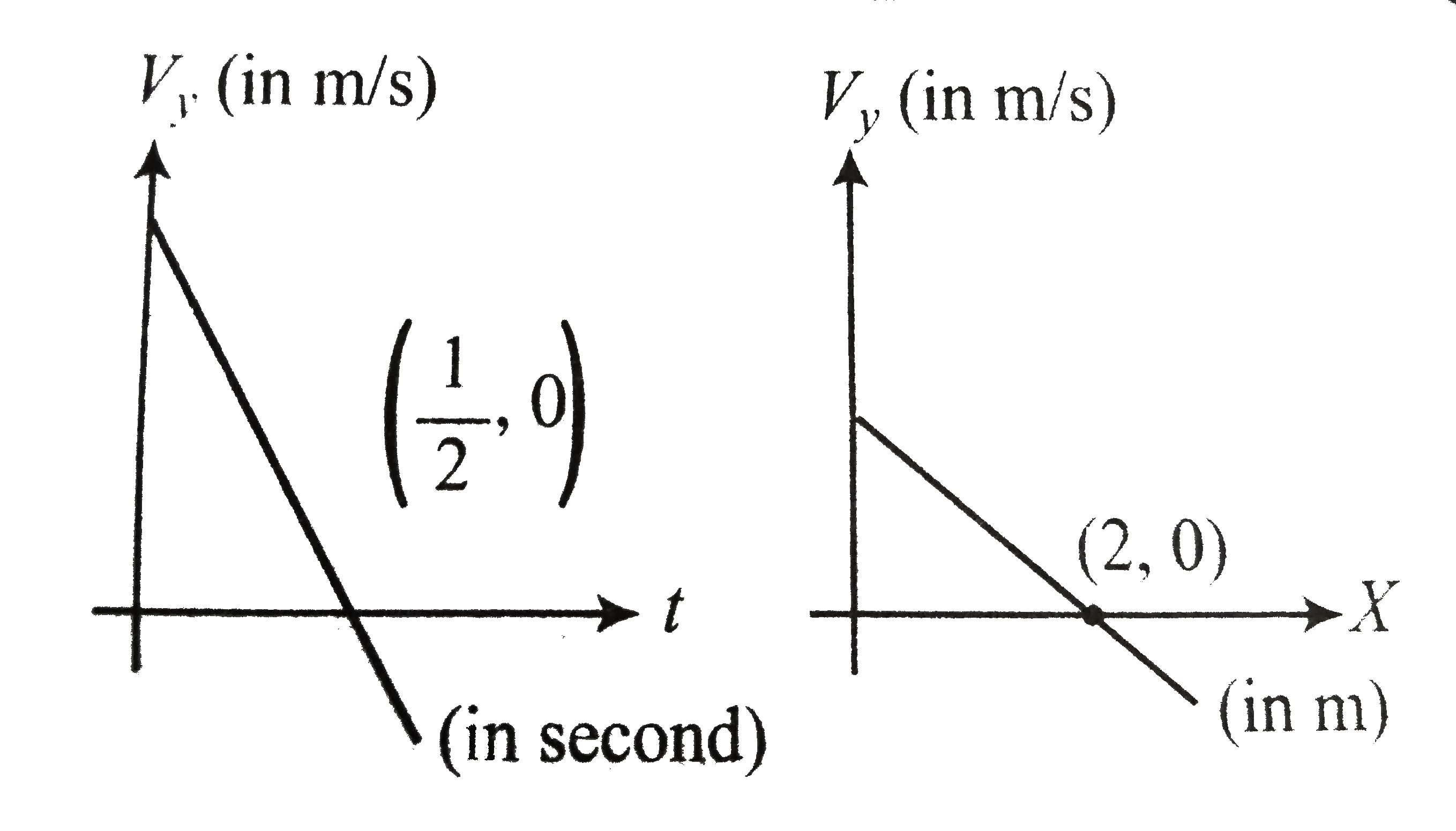 ,
, 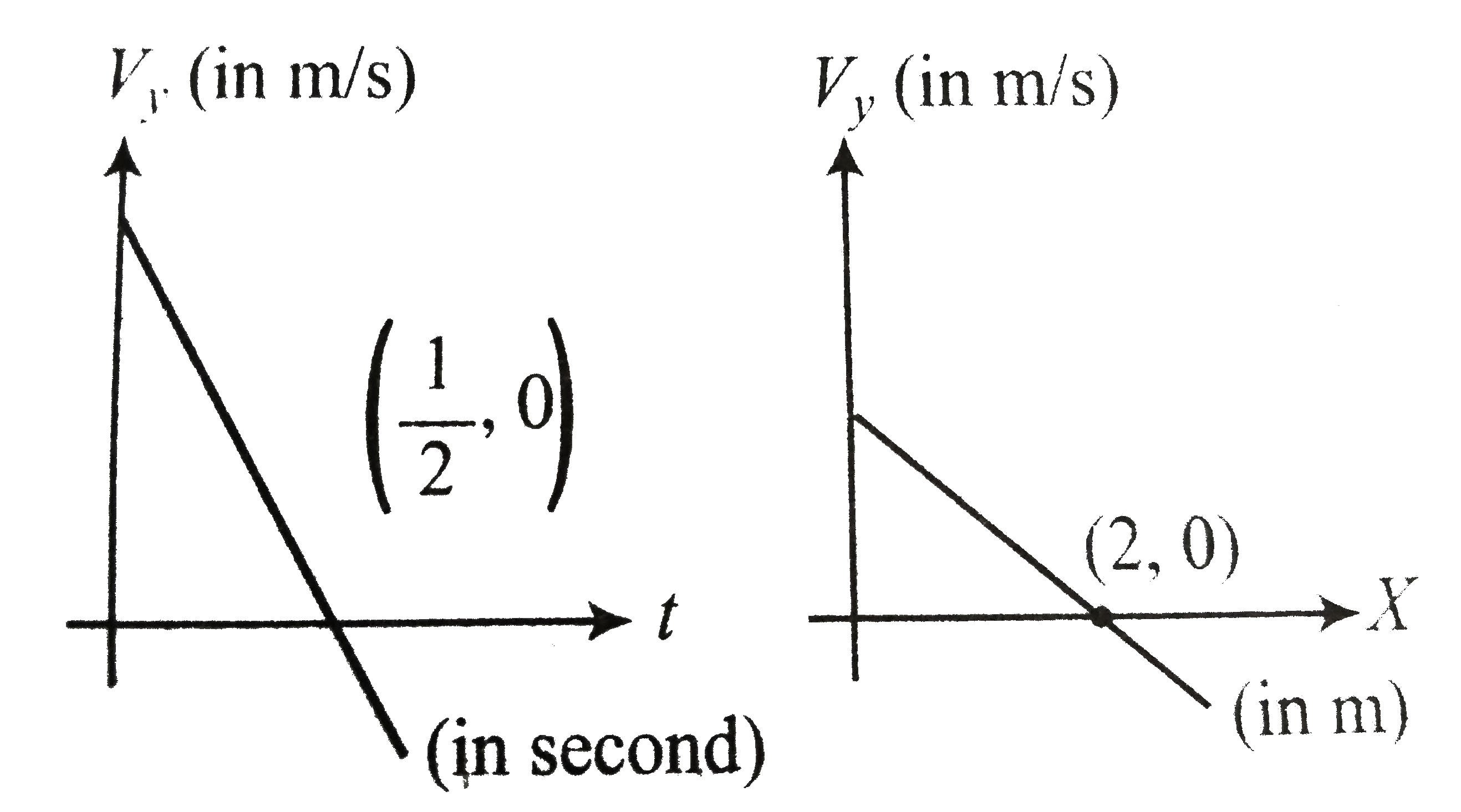
 ,
,