Subjective from CENGAGE PHYSICS (HINGLISH) RIGID BODY DYNAMICS 2 for Class 11
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS (HINGLISH) | Subjective |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A uniform spherical shell of mass M and radius R rotates, about a vertical axis on frictionless bearing. A massless cord passes around the equator of the shell., over a pulley of rotational inertia I and radius r and is attached to small object of mass m that is otherwise free to fall under the influence of gravity. There is no friction of pulley's axle, the cord does not slip on the pulley. What is the speed of the object after it has fallen a distance h. from rest? Use work-energy considerations.
 View Solution
View SolutionQuestion 2
A uniform rod of mass m and length l is kept vertical with the lower end clamped. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest position. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant? View SolutionQuestion 3
A rigid body is made of three identical thin rods, each with length fastened together in the form. of letter H. The body is free to rotate about a horizontal axis that runs along the length of one of the arms of H. The body is allowed to fall from rest from a position in which the plane of the H is horizontal. What is the angular speed of the body when the plane of H is vertical?
 View Solution
View SolutionQuestion 4
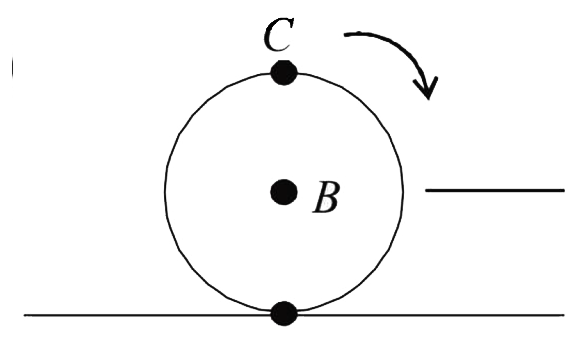
The steel balls A and B have a mass of 500g each and al rotating about the vertical axis with an angular velocity of 4rad/s at a distance of 15CM from the axis. Collar C is now forced down until the balls are at a distance 5CM from the axis. How Much work must be done move the collar down?
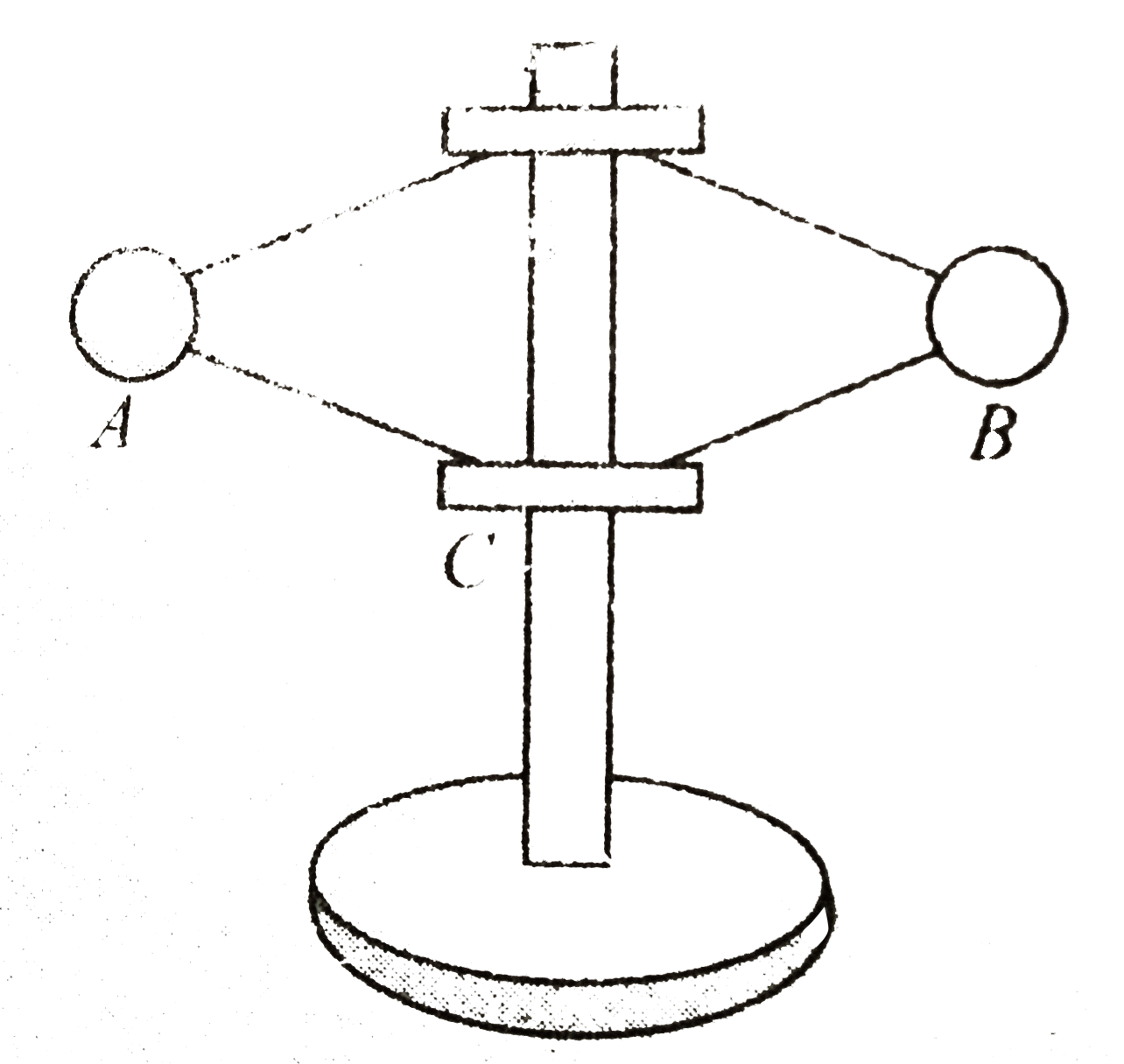 View Solution
View SolutionQuestion 10
A solid unifrom disk of mass m and radius R is pivoted about a horizontal axis through its centre and a small body of mass m is attached to the rim of the disk. If the disk is released from rest with the small body, initially at the same level as the centre, the angular velocity when the small body reaches the lowest point of the disk is.View SolutionQuestion 12
A circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
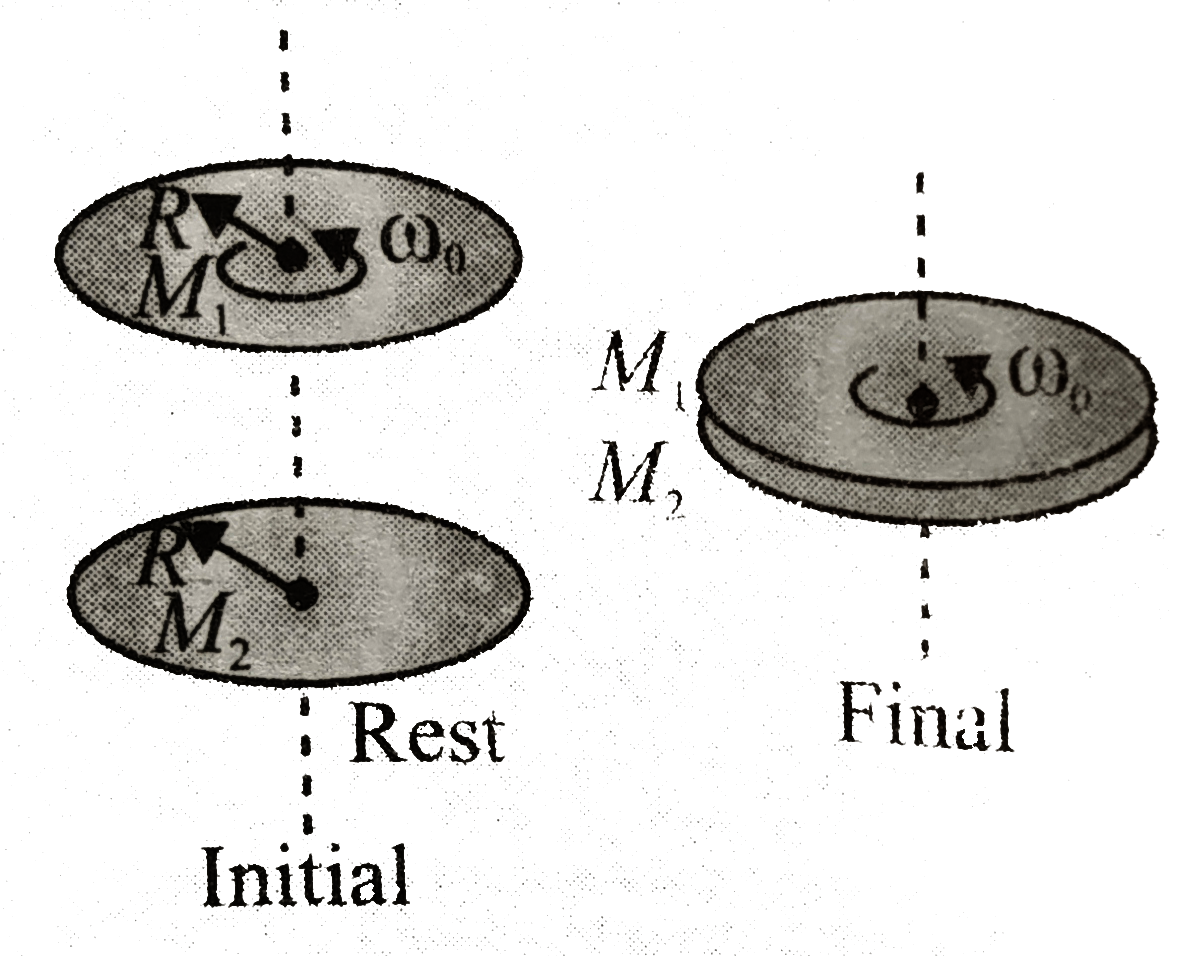 View Solution
View SolutionQuestion 13
A child of mass m is standing, on the periphery of a circular platform of radius R, which can rotate about its central axis. The moment of inertia of the platform is I. Child jumps off from the platform with a velocity u tangentially relative to the platform. Find the angular speed of the platform after the child jumps off.View SolutionQuestion 14
Suppose in the previous poroblem, the child stays at rest on the platform and one of hils firend throws a ball of mas m1 towards thim with a velocity of v from a direction tangential to the platform and the child on the platform catches the ball. Find the angular velocity of the platform after he catches the ball.View SolutionQuestion 15
Consider a cylinder rolling on a horizontal plane. Its linear velocity is v and rotational angular velocity is ω. Find its angular momentum about point P on the ground as shown in Fig. What happens to this angular momentum if the cylinder is rotating in opposite direction but moving translationally in the same direction.
 View Solution
View SolutionQuestion 17
Discs A and B are mounted on a shaft SS and may be connected or disconnected by a clutch C. The moment of inertia of disc A is one half that of disc B. With the clutch disconnected, A is brought up to an angular velocity ω0 .The accelerating torque is then removed from A and it is coupled to disc B by the clutch (Bearing friction may be neglected). It is found that 2000J of heat is developed in the clutch when the connection is made. What is the original kinetic energy of disc A? View SolutionQuestion 18

A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.View SolutionQuestion 20
Point masses m1andm2 are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω0 is minimum, is given by :
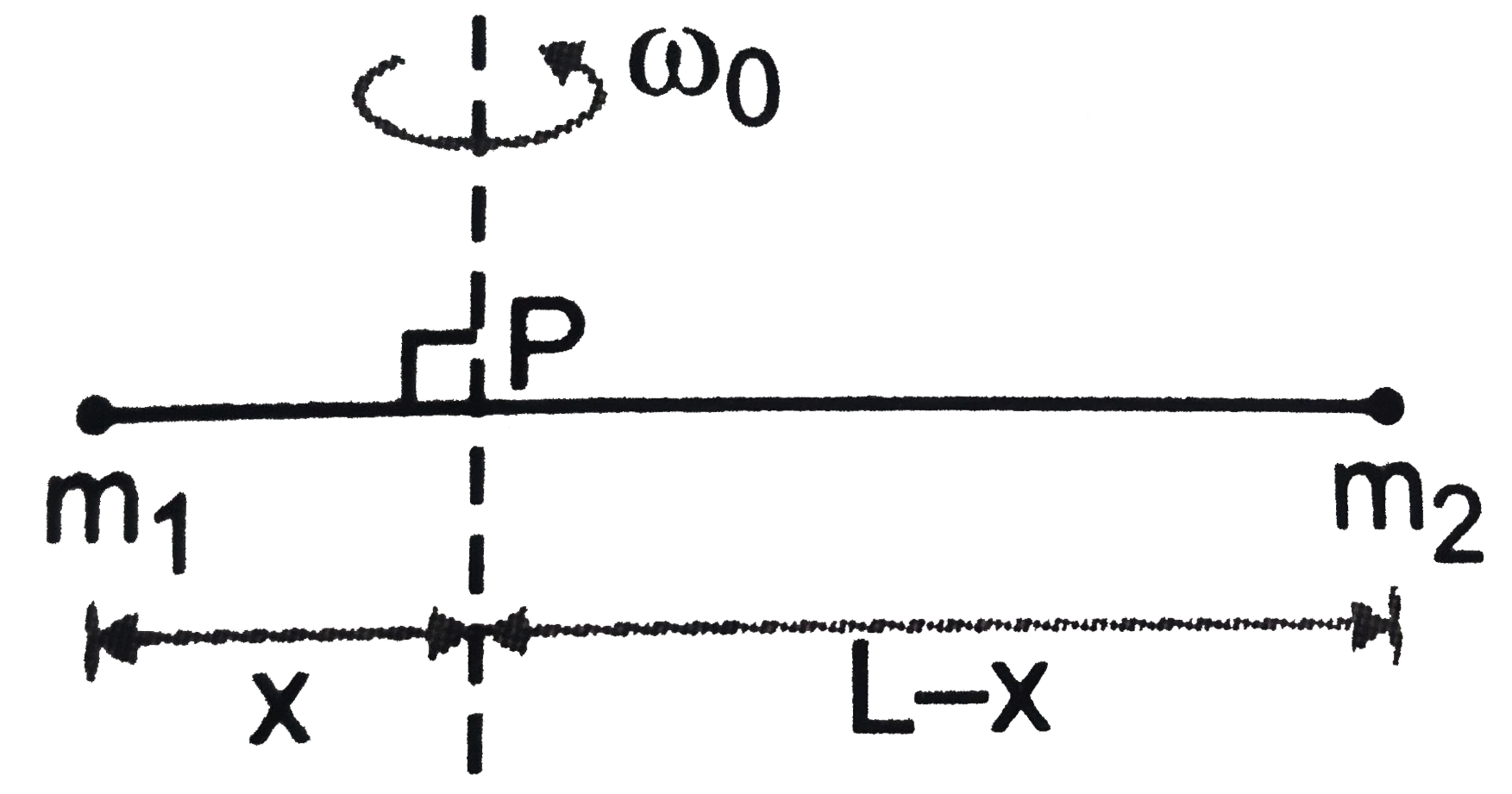 View Solution
View SolutionQuestion 21
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of the same dimensions but of mass M/4 is placed gently on the first disc co-axially. show that angular velocity o fthe system is 4ω/5.View SolutionQuestion 22
A thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass 0.5kg is tied and a block of mass 8.0kg is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from 8.0kg to 1.0kg, what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?
 View Solution
View SolutionQuestion 23
A girl jumps from a height h on the end of a see-saw. The see-saw consists of a uniform plank of length I pivoted at its centre. The plank is horizontal before the girl jumps. The mass of the see-saw is twice the mass of the girl. Find the angular velocity of the plank just after the girl jumps on the plank. View SolutionQuestion 24
The device shown in Fig. rotates on the vertical axle as shown. The frame has negligible mass as compared to the four masses each of mass m. Initial angular velocity of the system is ω0. Due to an internal mechanism the spokes in the frame lengthen so that the radii of the masses become 2a. Initially, it was a. What will be the new angular velocity of the system?
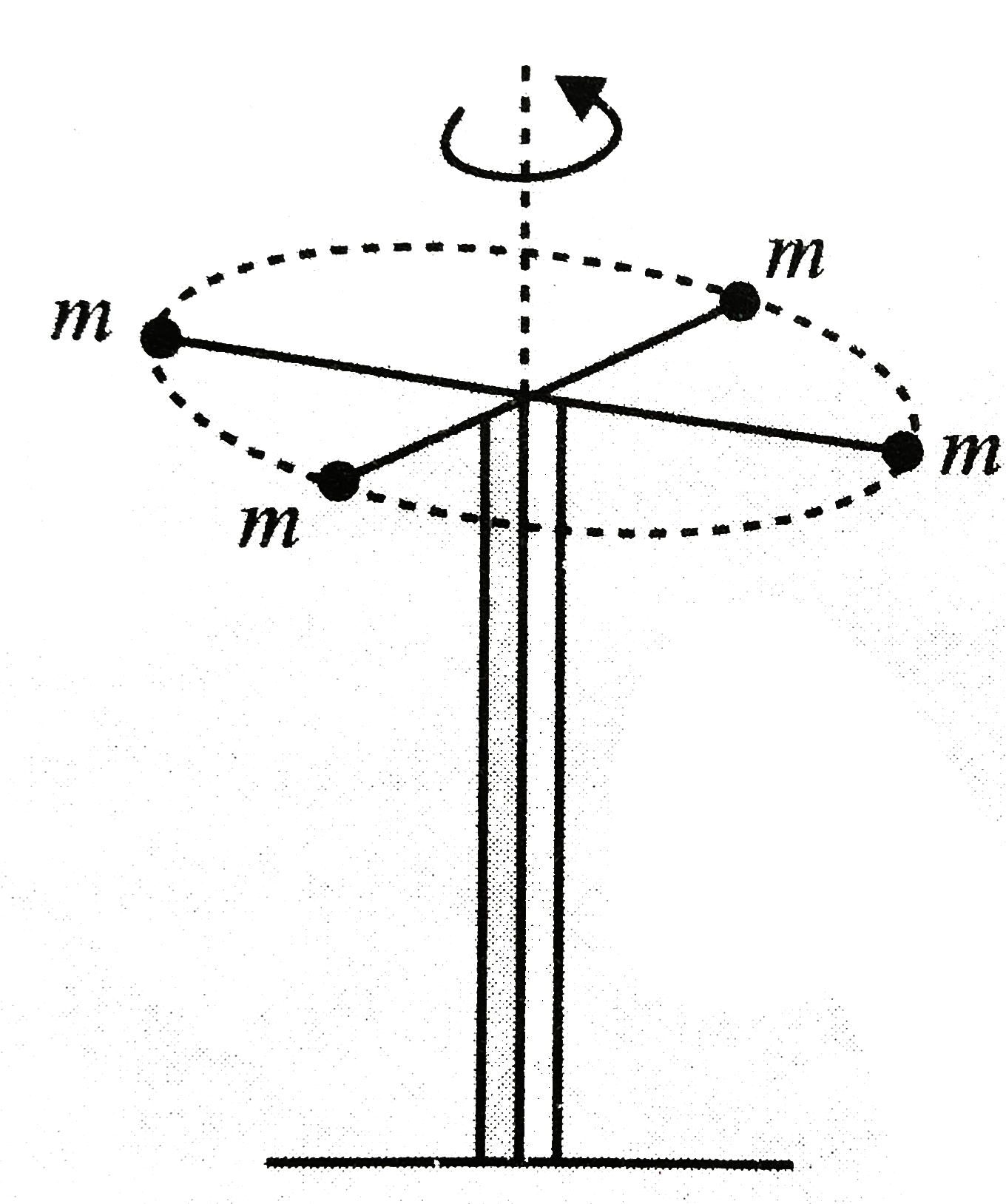 View Solution
View SolutionQuestion 25
Figure (a) and (b) shows two different arrangements of a spool being pulled with a constant force F in each case. Identify the direction of motion of the centre of mass, and the direction of friction force in each case.

a. The CM moves along……………….x-axis .
b. The friction force acts along…………………. x-axis.
c. The CM moves along .....x-axis.
d. The friction force acts along…………….. x-axis. View SolutionQuestion 26
A sphere moving with a velocity v0 on a smooth surface suddenly enters on a rough horizontal surface as shown in Fig. State which of the following statements are true or false
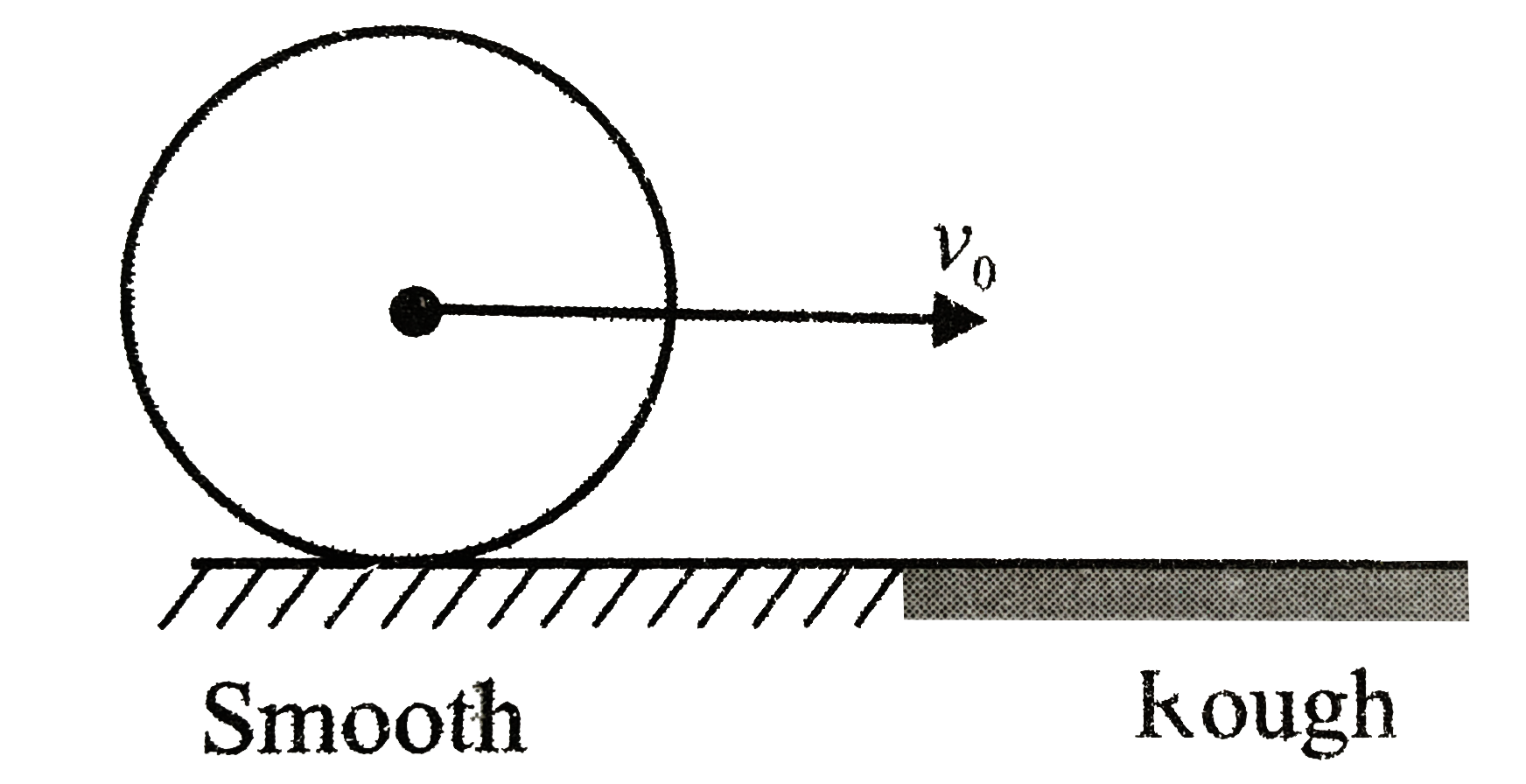
a. The sphere loses translational kinetic energy and gains rotational kinetic energy.
b. The total energy of the sphere is conserved.
c. The angular momentum of the sphere about any point OD the surface is conserved.
d. The final velocity attained by the centre of mass is 2v0/3.View SolutionQuestion 27
A cylinder of mass at and radius R rolls on a stationary plank of mass M. The lower surface of the plank is smooth and the upper surface is sufficiently rough with a coefficient of friction μ. A man is to hold the plank stationary with respect to the ground, as shown Fig.
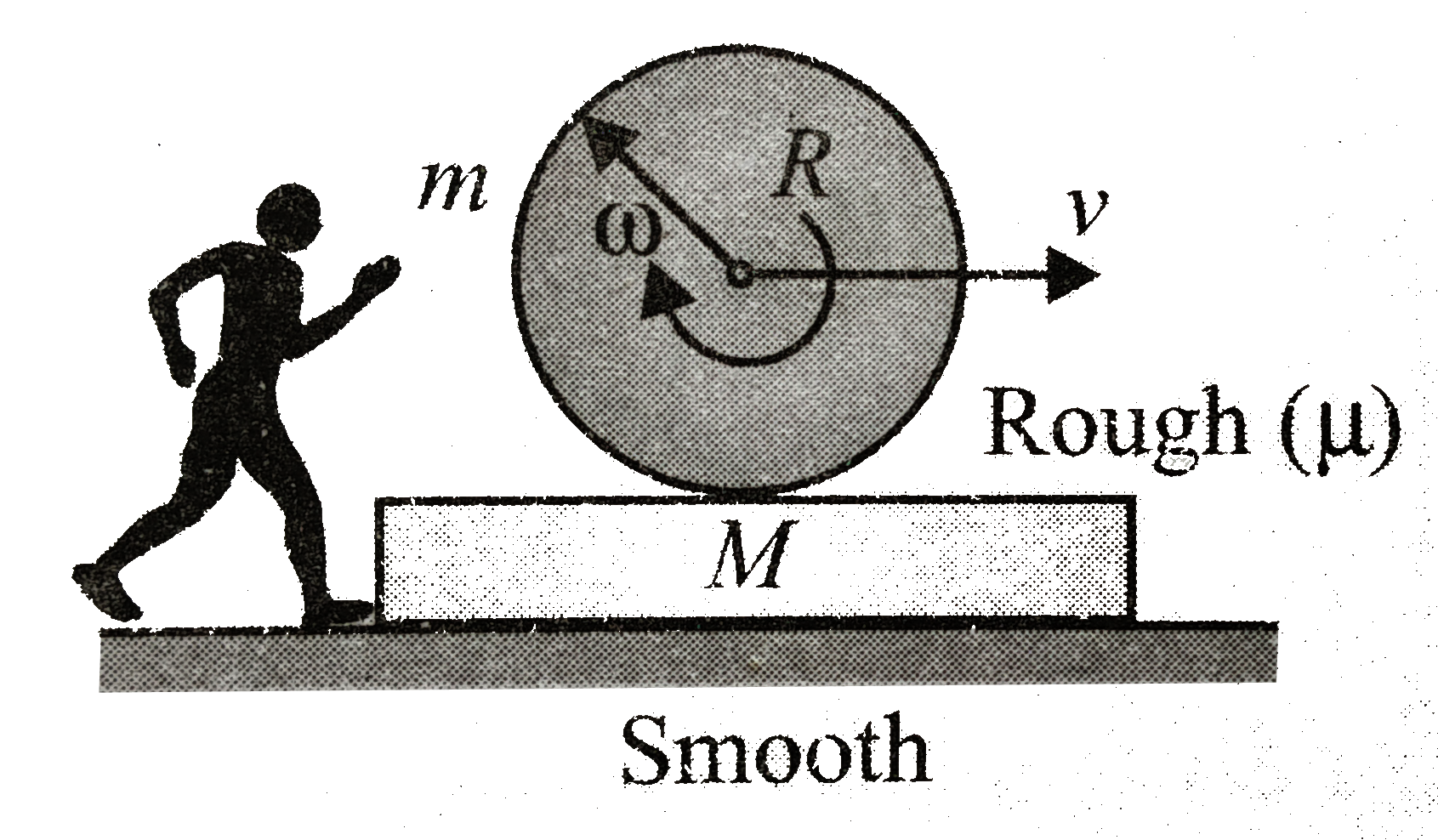
The force exerted by the man to keep the plank stationary is equal to……View SolutionQuestion 29
A constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel? View SolutionQuestion 30
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
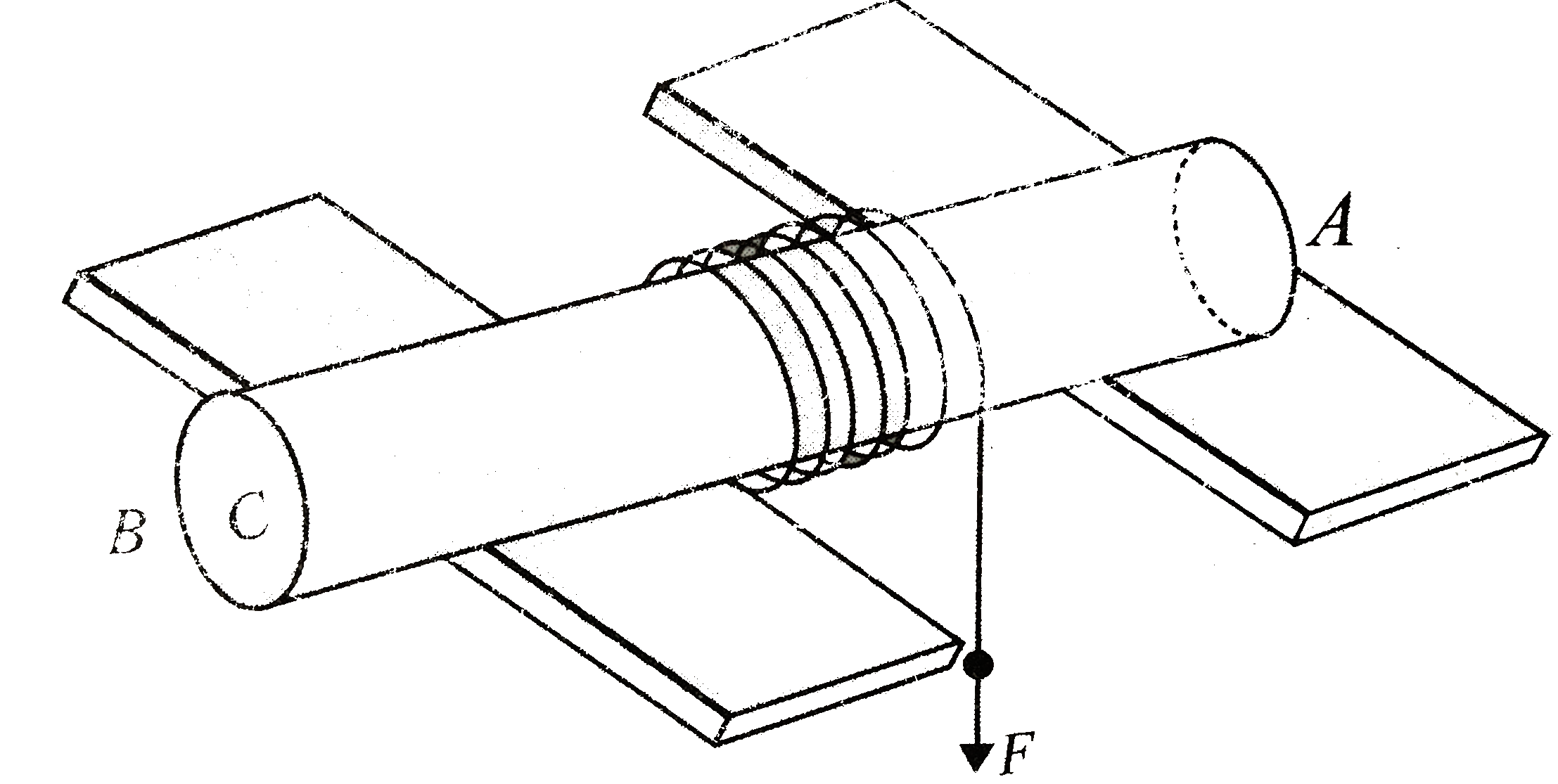
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks? View SolutionQuestion 31
A load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.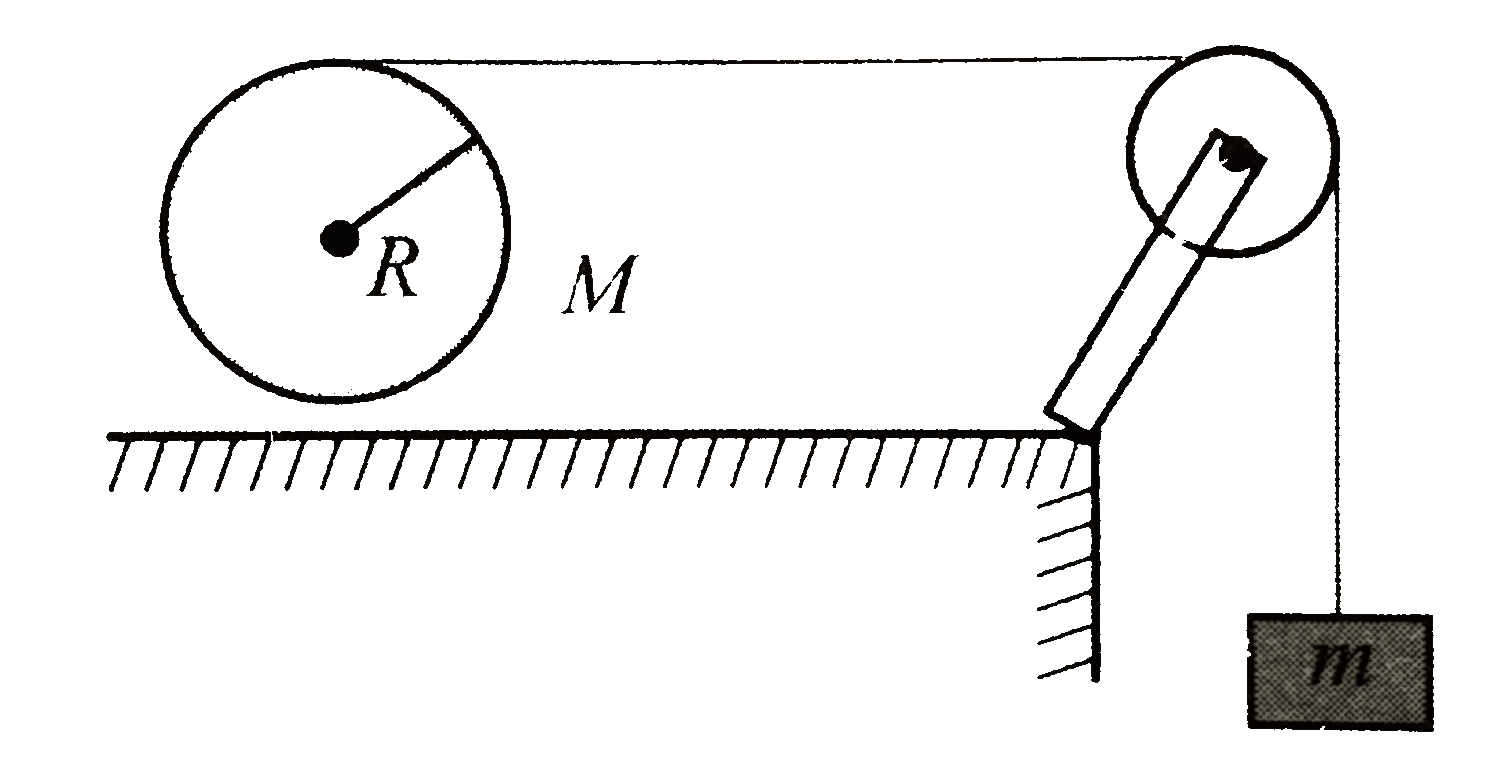
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls alwaysView SolutionQuestion 33
A spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.
 View Solution
View SolutionQuestion 34
A solid cylinder wheel of mass M and radius R is pulled by a force F applied to the centre of the wheel at 37∘ to the horizontal. If the wheel is to roll without slipping, what is the maximum value of |F| ? The coefficients of static and kinetic friction are μs=0.40 and mk=0.30.(sin37∘=35)View SolutionQuestion 35
Find the acceleration of a system consisting of a cylinder of mass m and radius R and a plank of mass M placed an a smooth surface if it is pulled with a force F as shown Fig. Given that sufficient friction is present between the cylinder and the plank surface to prevent sliding of the cylinder.
 View Solution
View SolutionQuestion 36
A uniform solid cylinder of mass m rests on two horizontal planks as shown in Fig. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically up with a force F. What is the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to μ. What is the maximum acceleration of the axis of the cylinder?
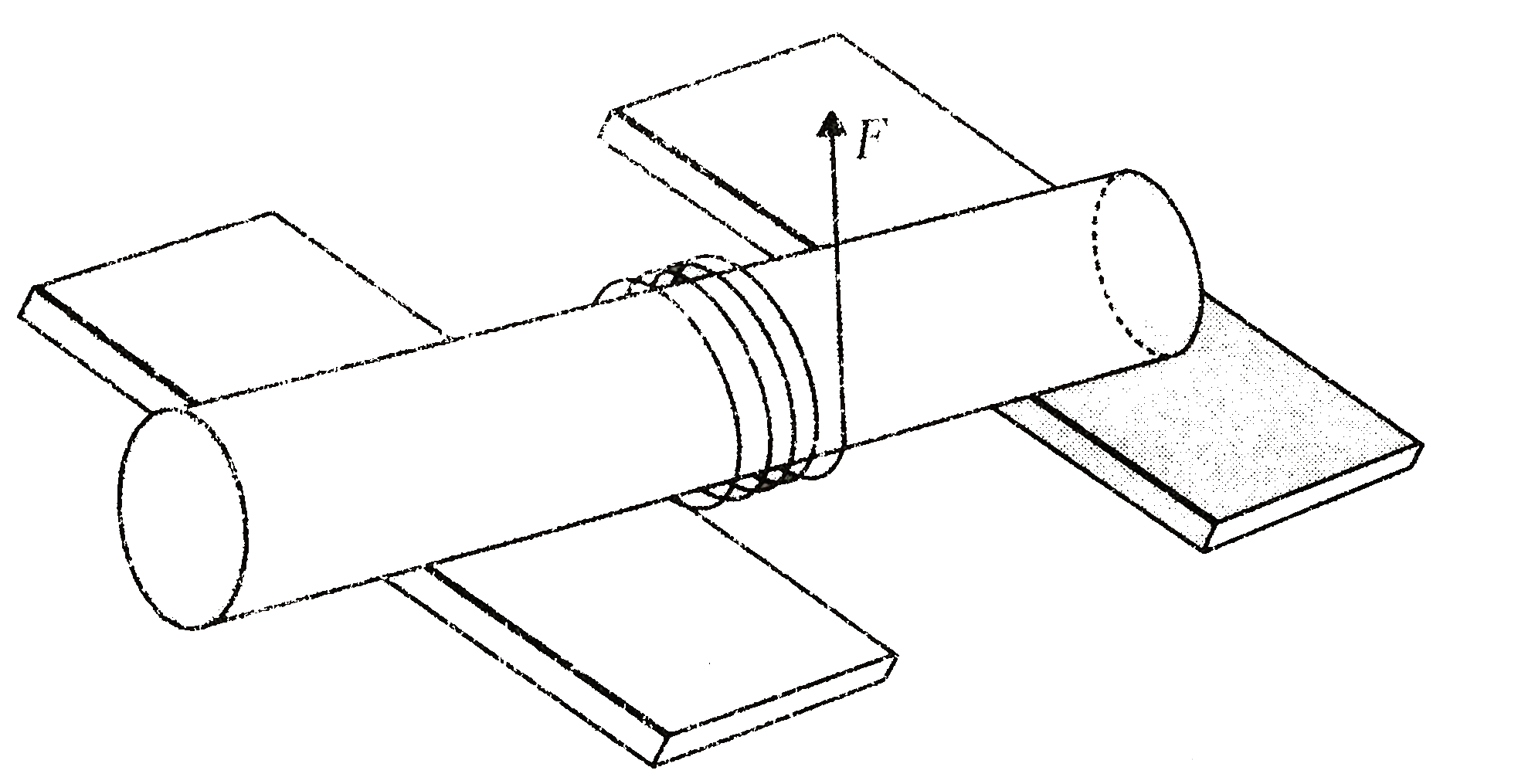 View Solution
View SolutionQuestion 37
A bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.
 View Solution
View SolutionQuestion 40
A ball of mass m is released from rest from a height H along a smooth, light and fixed tube having a semicircular portion so that the ball just reaches the top of the semicircle.
a. Find the radius of the semi-circle.
b. Find the maximum force imparted by the ball on the ground.
 View Solution
View SolutionQuestion 46
A sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.View SolutionQuestion 47
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively, strike the bar (as shown in figure) and stick to the bar after collision. Calculate (a) velocity of the centre of mass (b) angular velocity about centre of mass and (c) total kinetic energy, just after collision.
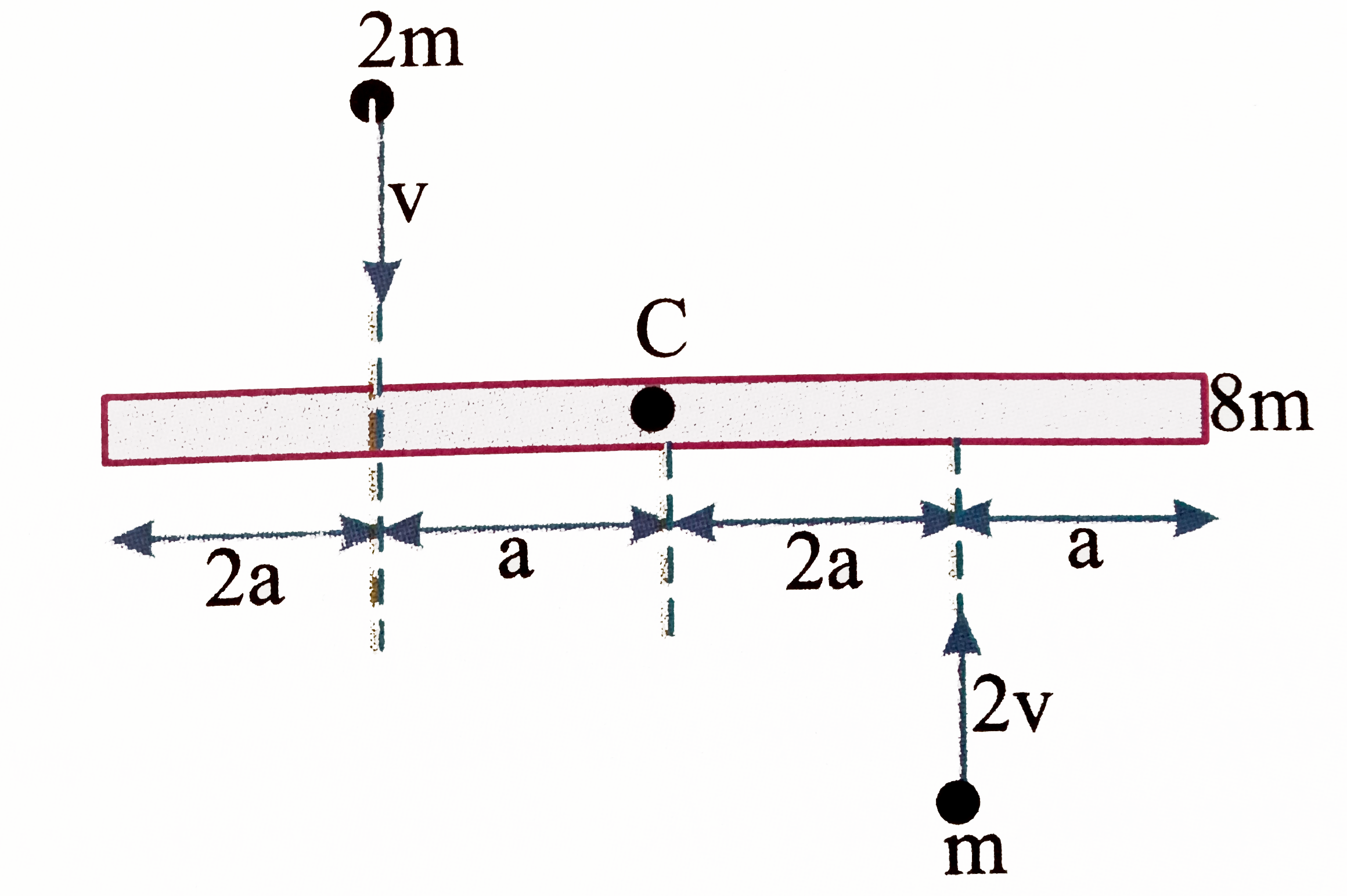 View Solution
View SolutionQuestion 48
A circular wooden hoop of mass m and radius R rests fiat on a frictionless surface. A bullet, also of mass m and moving with a velocity v, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than R. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
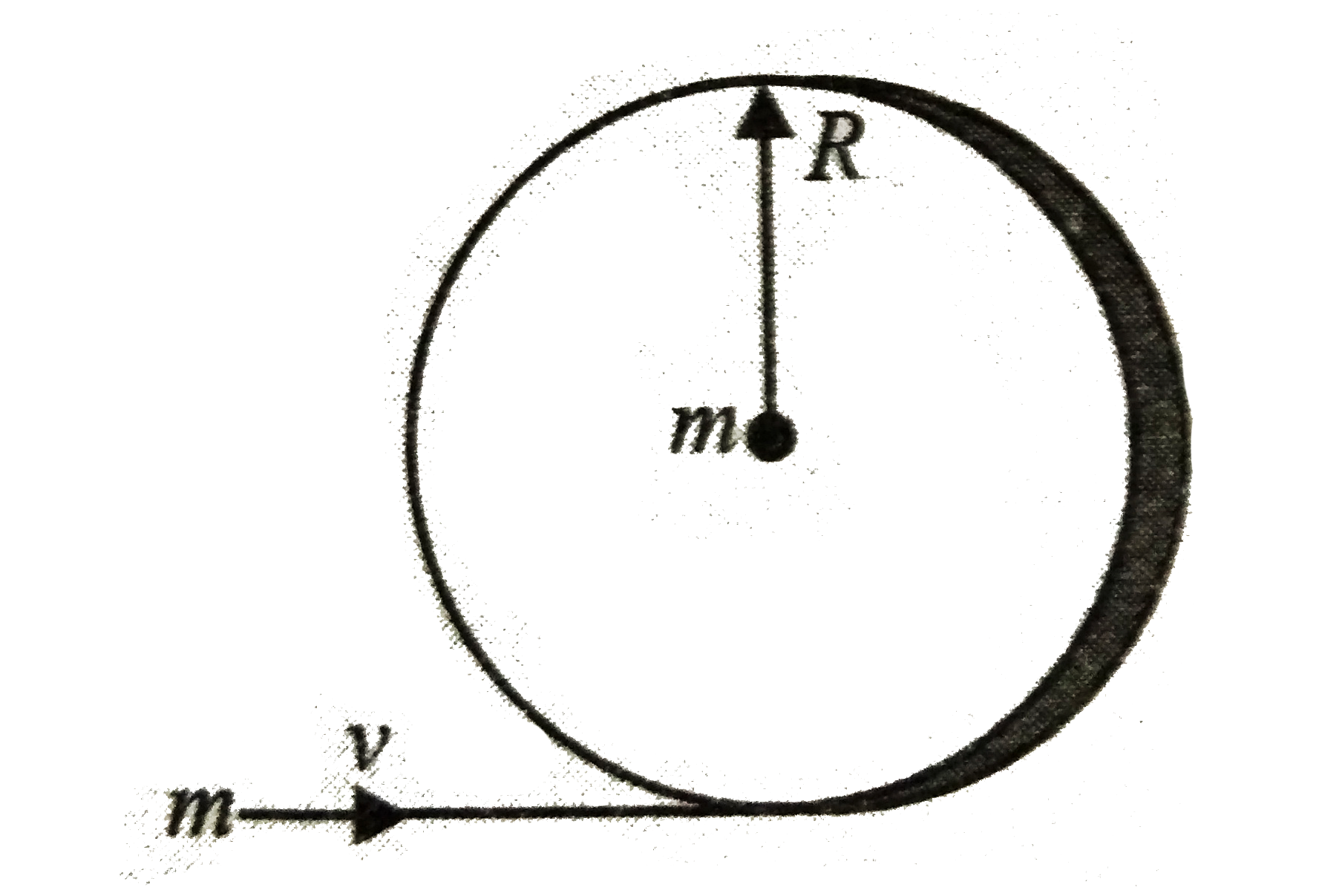 View Solution
View SolutionQuestion 49
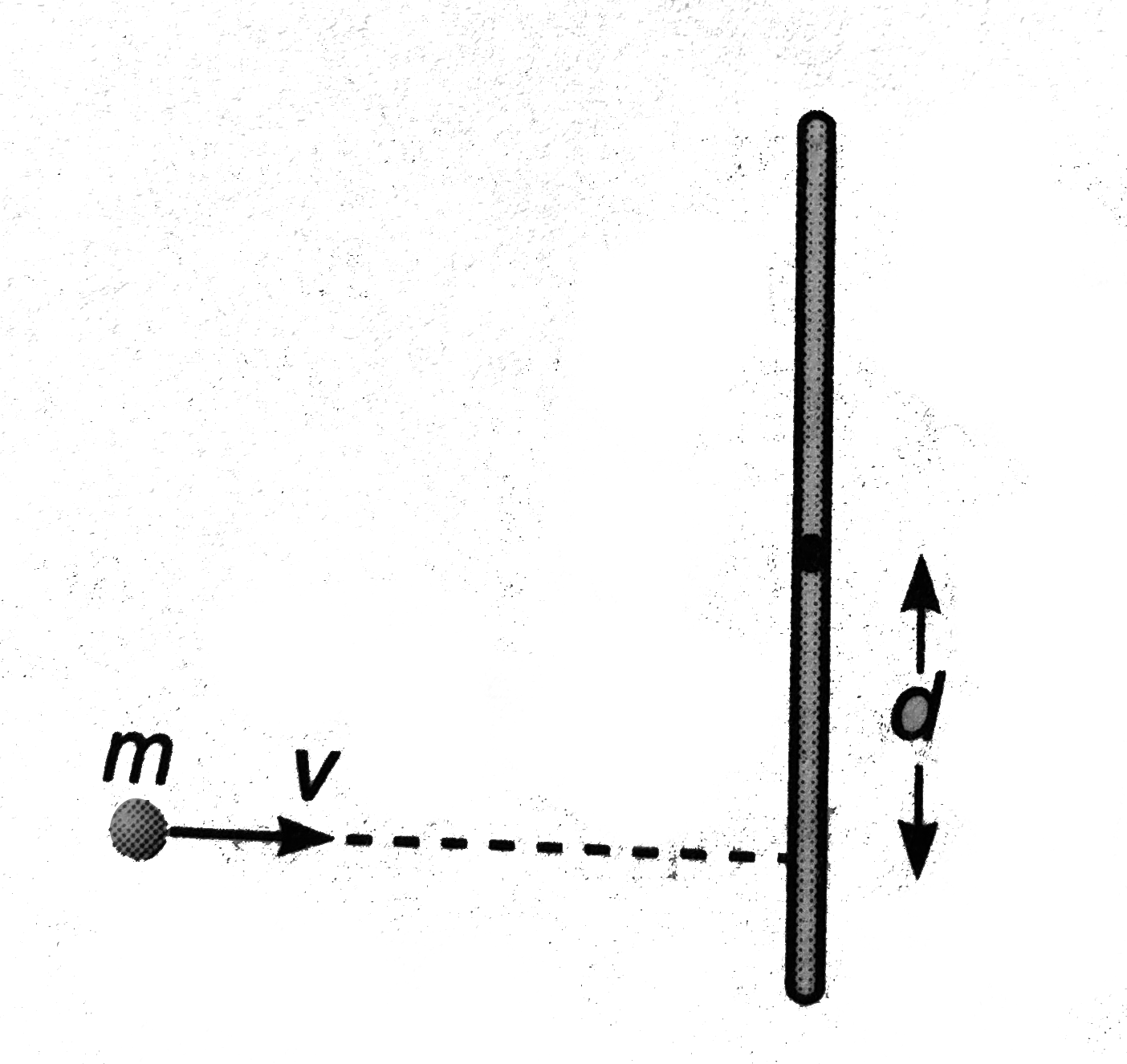
A stick of length l lies on horizontal table. It has a mass M and is free to move in any way on the table. A ball of mass m moving perpendicularly to the stick at a distance d from its centre with speed v collides elastically with it as shown in figure. What quantities are conserved in the collision ? what must be the mass of the ball, so that it remains at rest immediately after collision?View SolutionQuestion 50
A thin uniform rod of length l is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect. View SolutionQuestion 53
Two identical particles B and C each of mass 50g are connected by a light rod of length 30CM. Another particle A of same mass moving With a speed u=60CM/s strikes B, in a direction perpendicular to AB, and sticks to it. The whole process takes place on a smooth horizontal plane. Find the angular velocity ω of the system about its centre of mass, immediately after the impact.
 View Solution
View SolutionQuestion 54
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of A mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
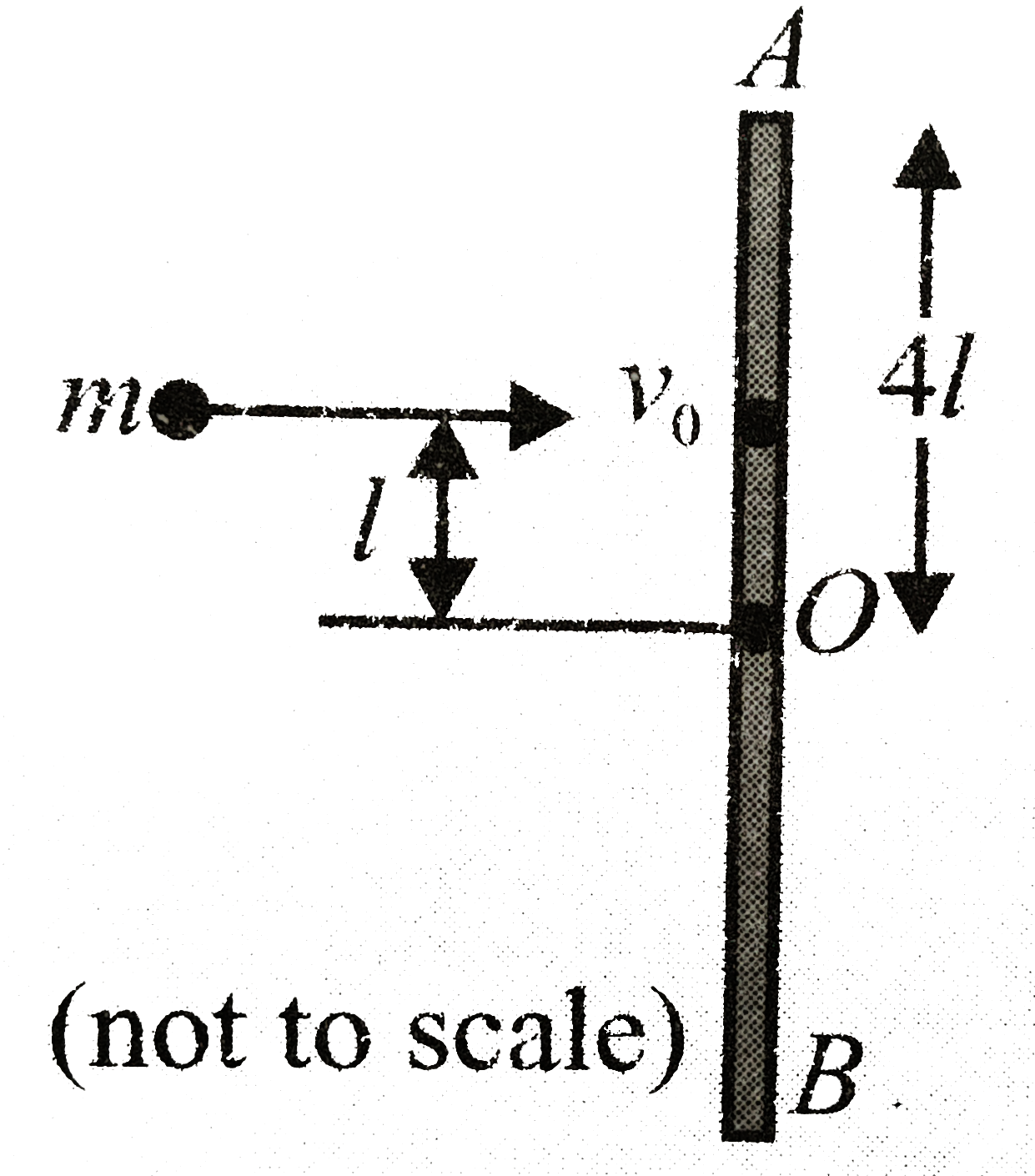 View Solution
View SolutionQuestion 55
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find (a). the velocity of the centre of the rod and (b). the angular velocity of the rod abut its centre just after the collision. View SolutionQuestion 56
In the shown figure a mass m slides down the frictionless surface from height h and collides with the uniform vertical rod of length L and mass M after collision the mass m sticks to the rod. The rod is face to rotate in a vertical plane about fixed axis through O. Find the maximum angular deflection of the rod from its initial position.
 View Solution
View SolutionQuestion 57
A small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.
 View Solution
View SolutionQuestion 58
A thin uniform rod of length l is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect. View SolutionQuestion 59
A uniform thin circular ring of mass m(m=0.4kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.
 View Solution
View SolutionQuestion 61
A spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
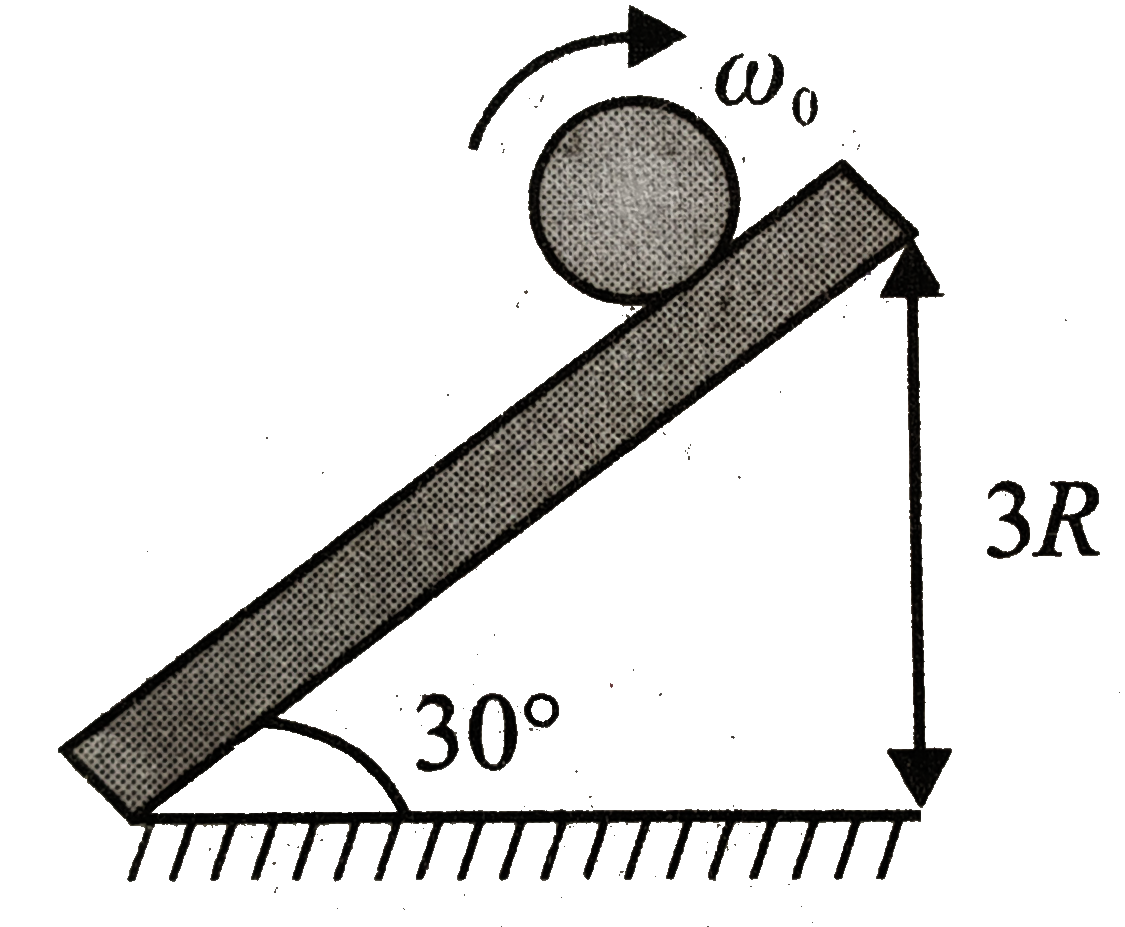 View Solution
View SolutionQuestion 62
A hoop of mass m is projected on a floor with linear velocity v0 and reverse spin ω0. The coefficient of friction between the hoop and the ground is μ.
a. Under what condition will the hoop return back?
b. How far will it go?
c. How long will it continue to slip when its centre of mass becomes stationary?
d. What is the velocity of return?View SolutionQuestion 65
A uniform disc is spun with an angular velocity ω and simultaneously projected with a linear velocity v towards left on a plank, while the plank moves towards right with a constant velocity 2v. If the disc rolls without sliding on the plank just after its spinning, find the magnitude of →ω. (Take v=3ms−1,R=1m)
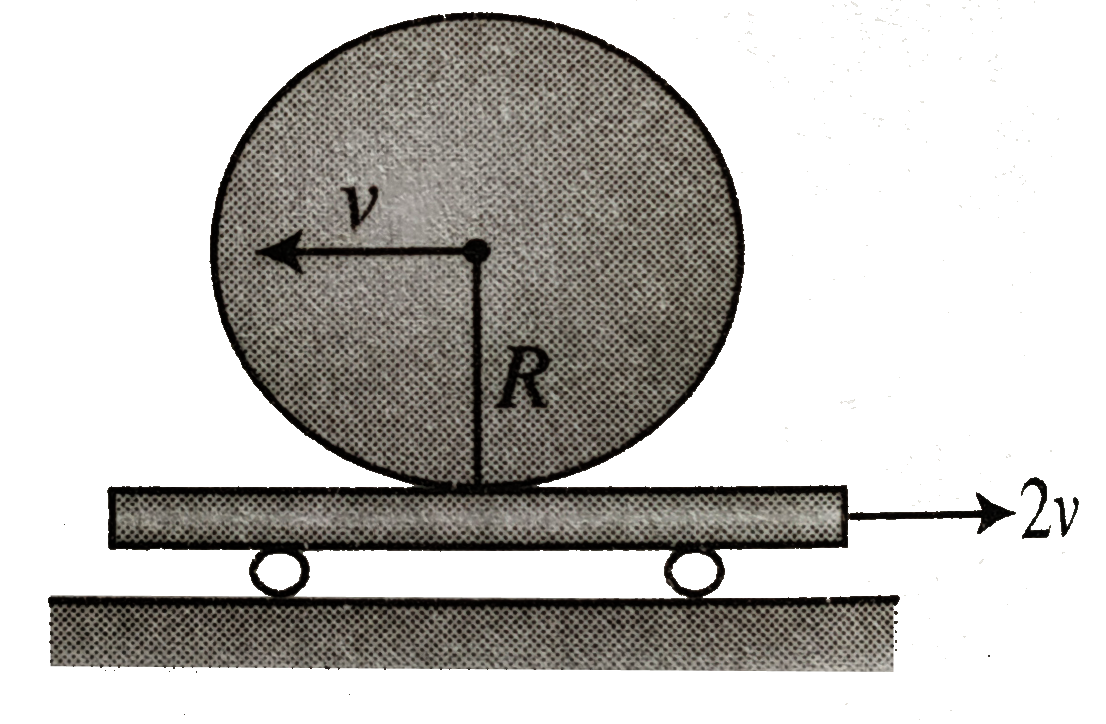 View Solution
View SolutionQuestion 66
A spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
 View Solution
View SolutionQuestion 67
A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity v0. At what values of v0 will the hoop move without bouncing?
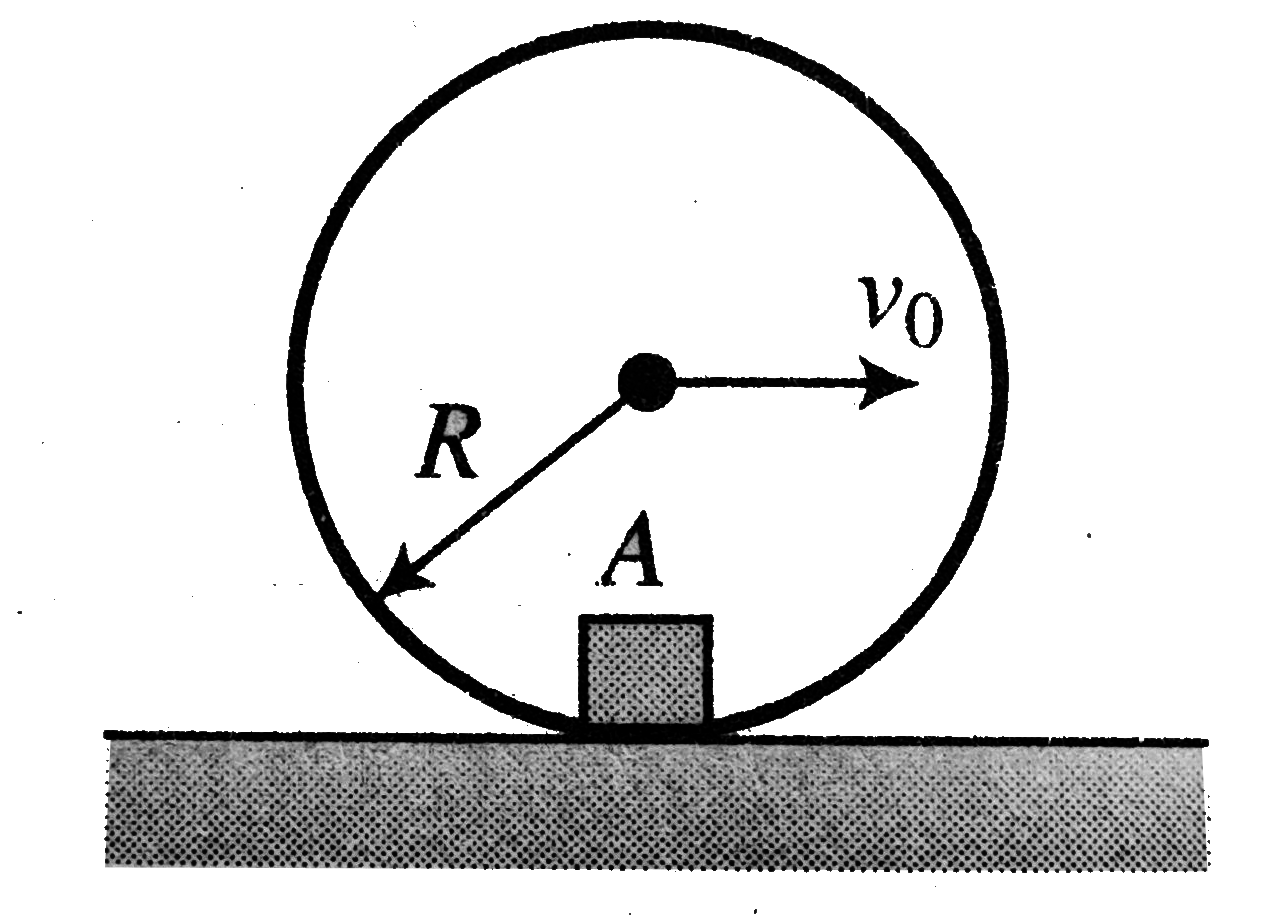 View Solution
View SolutionQuestion 70
A uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
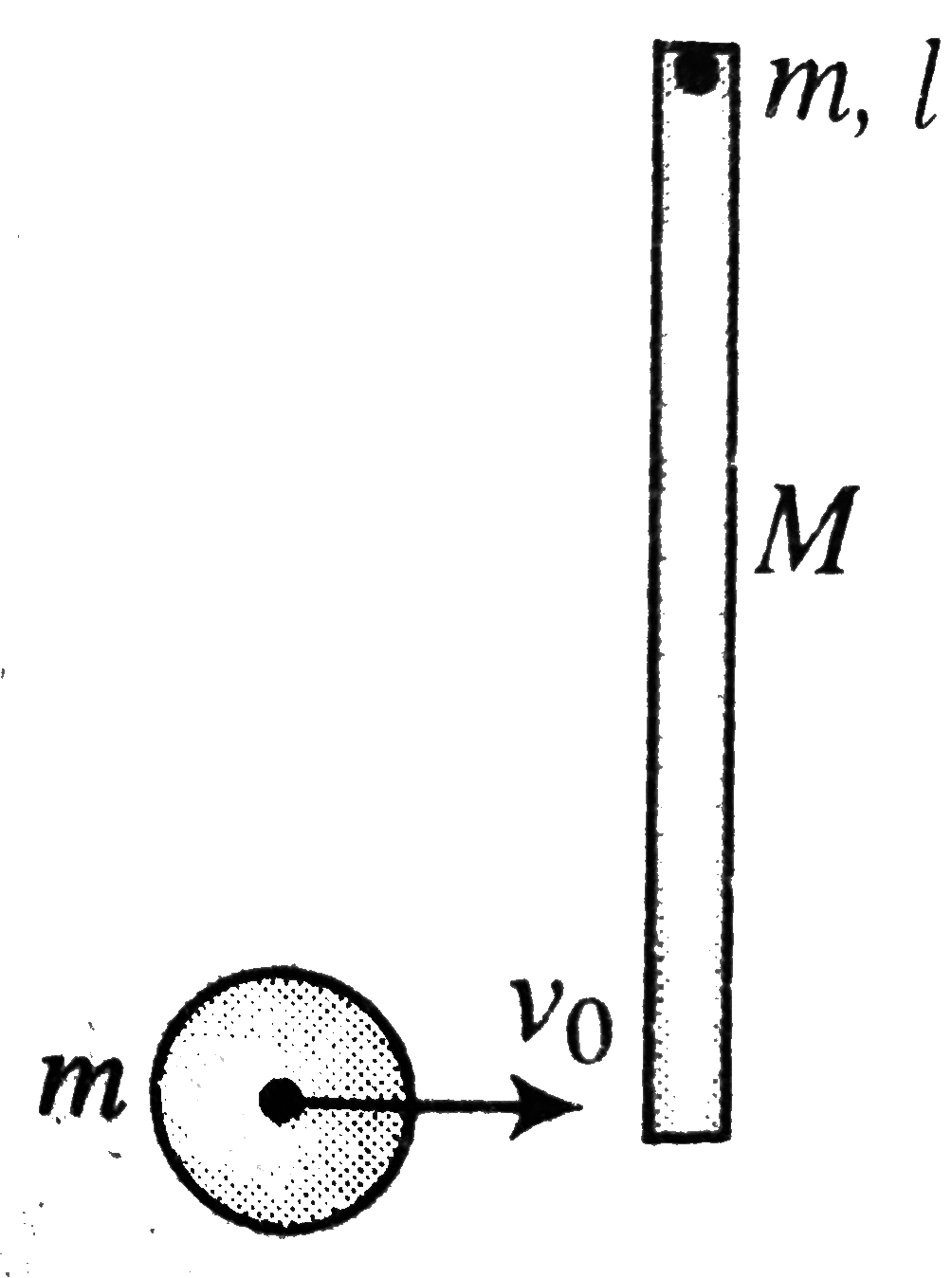 View Solution
View SolutionQuestion 71
A cylinder of mass m is kept on the edge of a plank of mass 2m and length 12m, which in turn is kept on smooth ground. Coefficient of friction between the plank and the cylinder is 0.1. The cylinder is given an impulse, which imparts it a velocity 7ms−1 but no angular velocity. Find the time after which the cylinder falls off the plank.
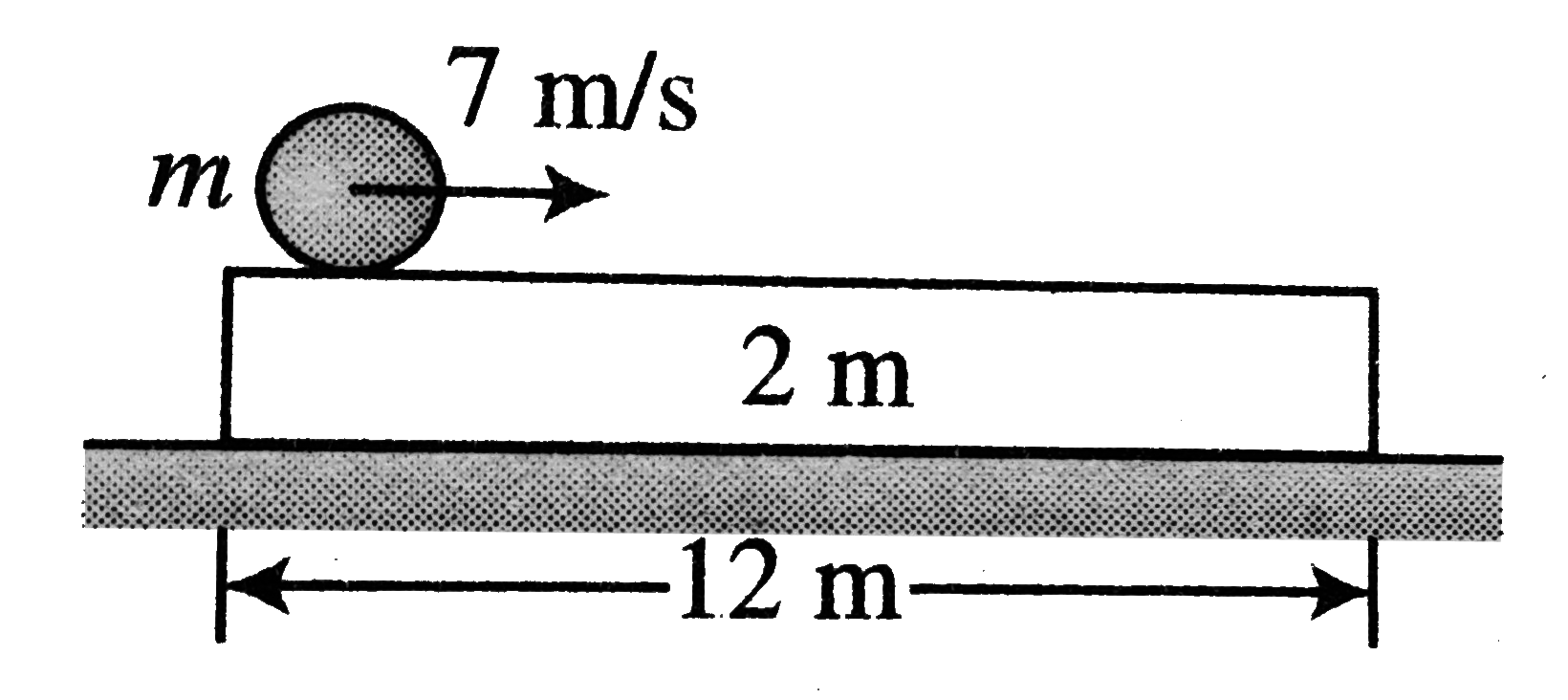 View Solution
View SolutionQuestion 73
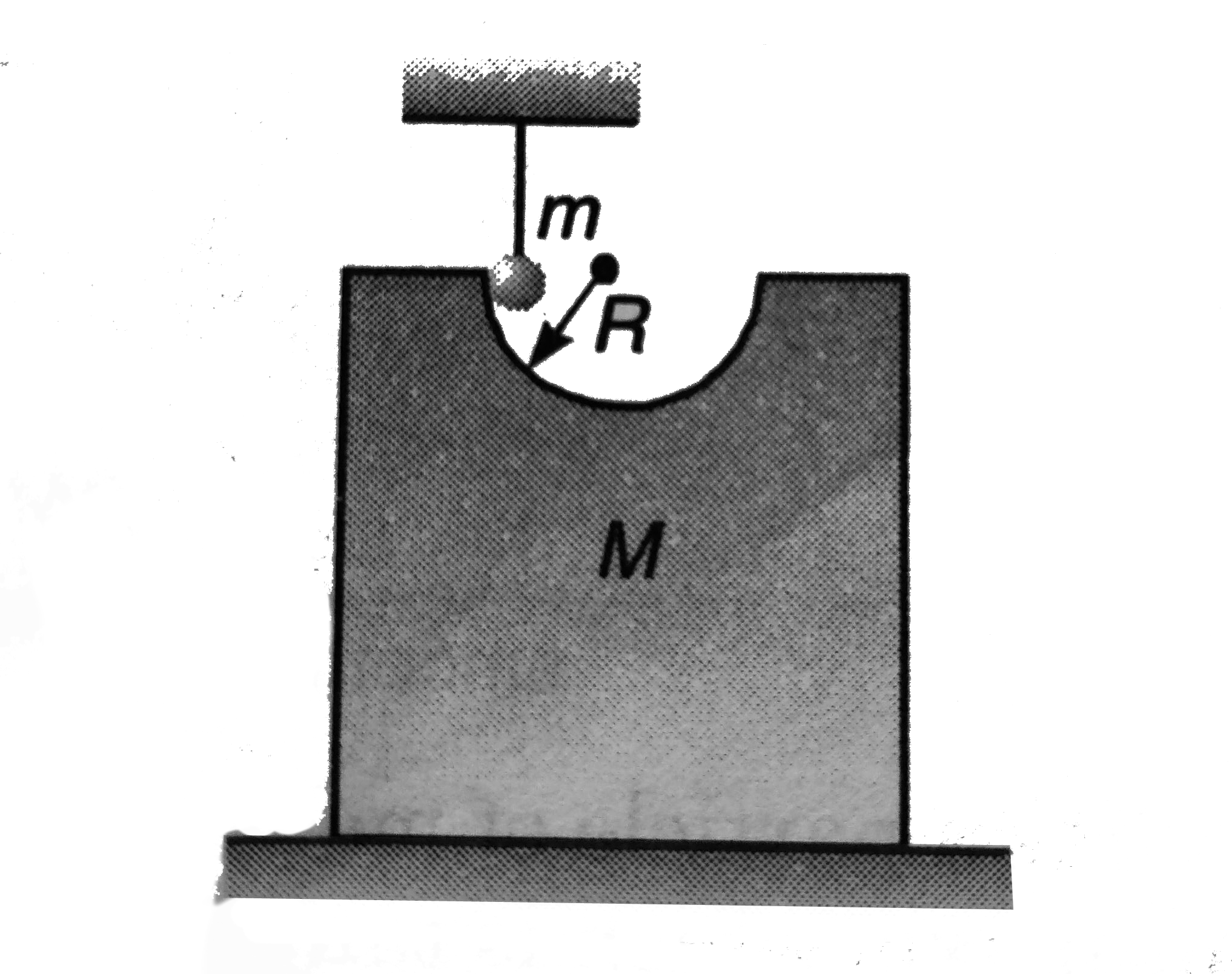
A semicircular track of radius R=62.5cm is cut in a block. Mass of block having track, is M=1kg and rests over a smooth horizontal floor. A cylinder of radius r=10cm and mass m=0.5kg is hanging by thread such that axes of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip.
Calculate velocity (in m/s) of the block when it reaches bottom of the track. (g=10m/s2)View SolutionQuestion 74
A solid spherical ball rolling without slipping collides elastically with an identical ball at rest, as shown in the figure. Assuming that the frictional forces are small enough to have negligible effect during the instant of collision, calculate, the velocity of each ball along enough time after the collision when each ball is again rolling without slipping.
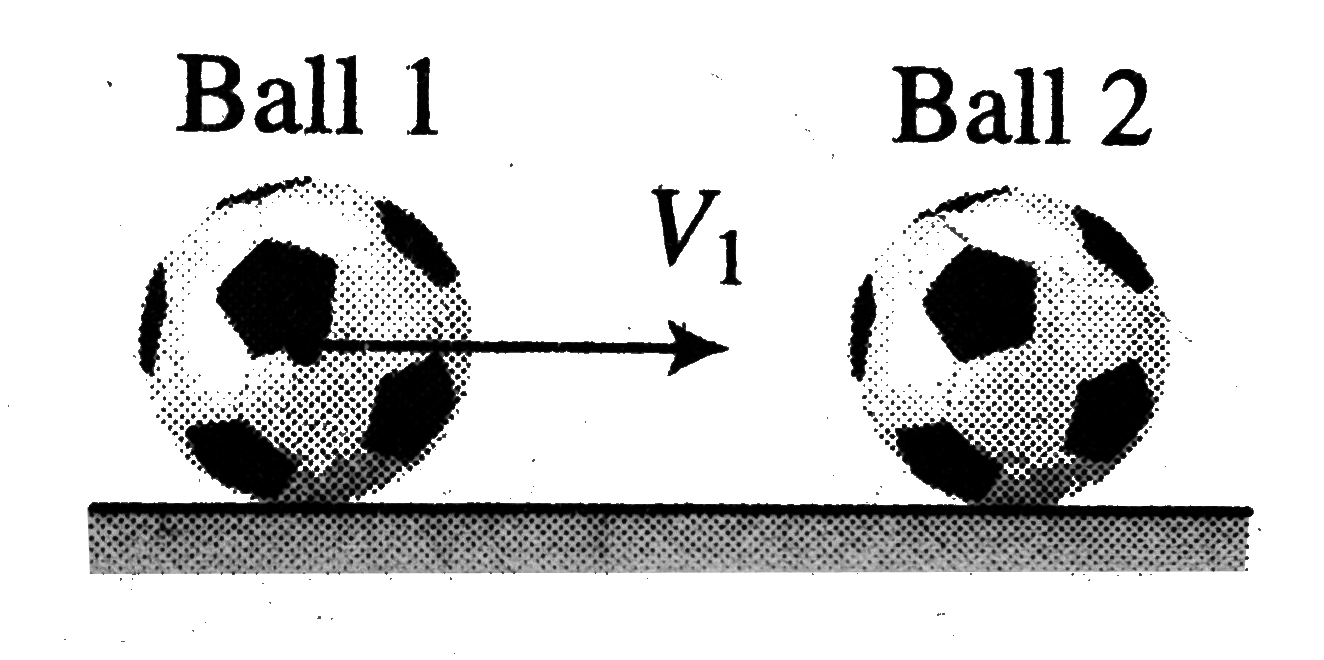 View Solution
View SolutionQuestion 75
A uniform rod of mass m and length l is released from rest from its vertical position by giving a gently push. In consequence, the end of the rod collides at P after rotating about the smooth horizontal axis O. If the coefficient of restitution e=(12). Find the: a. angular speed of the rod just after the impact.
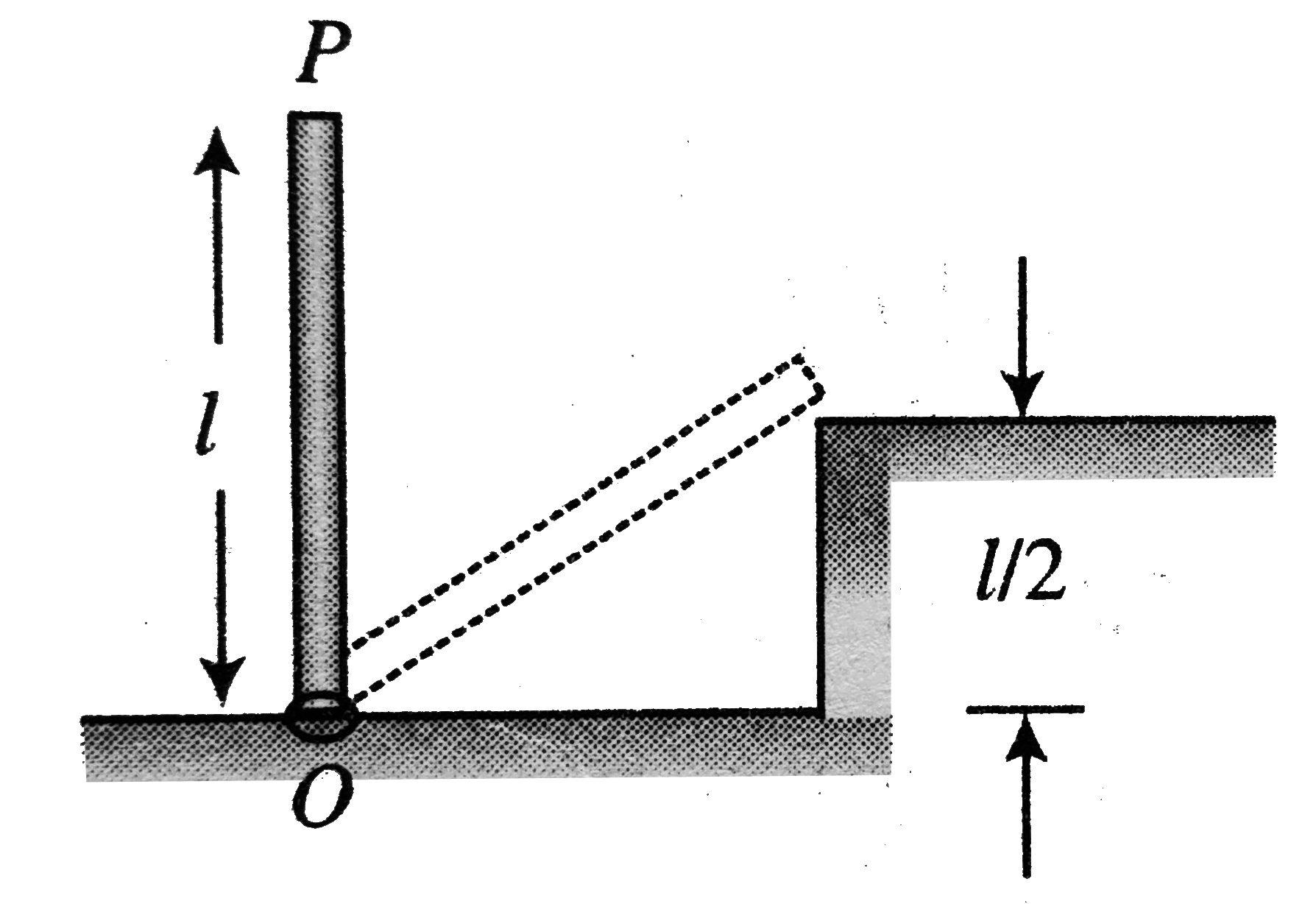
b. energy loss during collision. c. maximum angle rotated collision. View SolutionQuestion 77
Figure shows a cubical wooden block of side length a and mass M which is resting over a horizontal surface and constrained to rotate about its right lower edge D. A bullet of mass m moving horizontally, directly towards its centre with velocity v strikes and gets embedded in it. During subsequent motion the block just topples, calculate v. Assume m<<M.
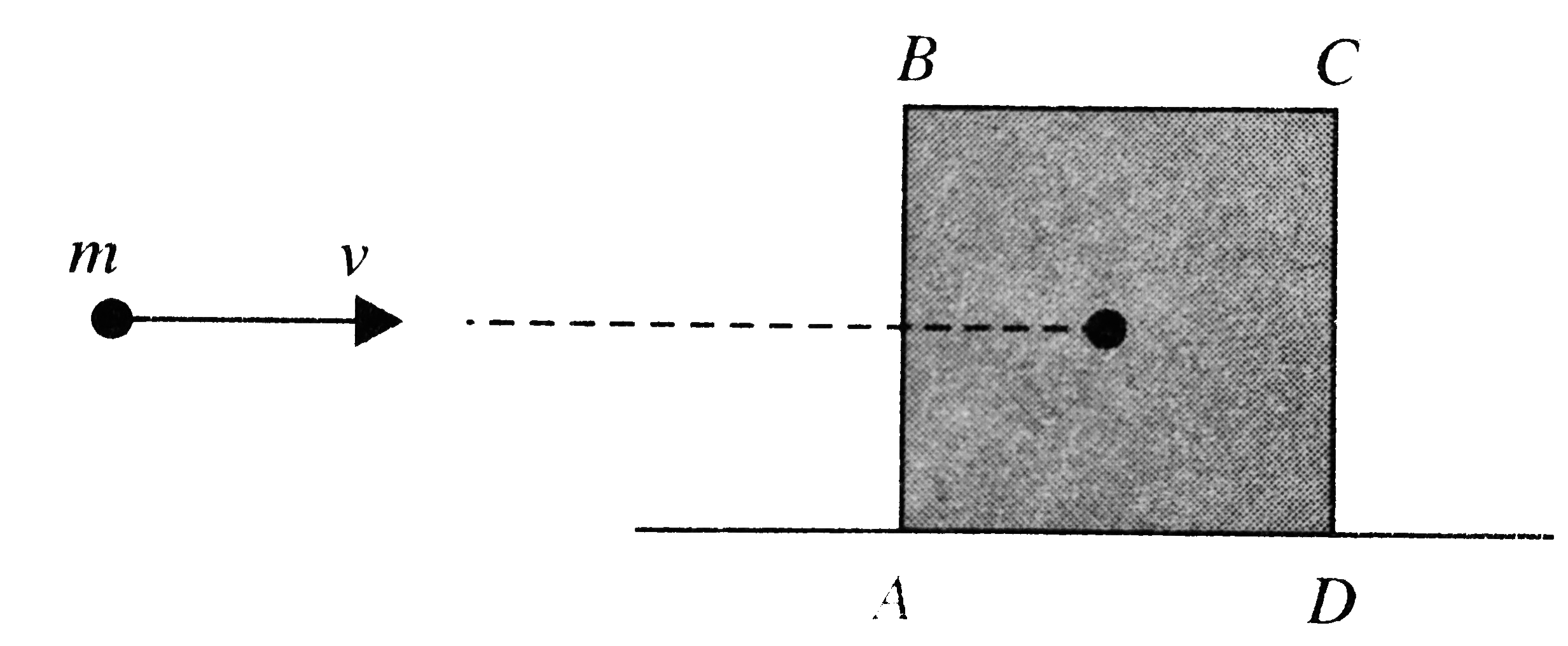 View Solution
View SolutionQuestion 86
A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 View Solution
View SolutionQuestion 96
A uniform sphere of mass m radius r and moment of inertia I about its centre moves along the x-axis as shown in Fig Its centre of mass moves with velocity =v0, and it rotates about its centre of mass with angular velocity =ω0. Let →L=(Iω0+mv0r)(−k). The angular momentum of the body about the origin O is
 View Solution
View SolutionQuestion 99
A uniform rod AB of length l and mass m hangs from point A in a car moving with velocity v0 on an inclined plane as shown in Fig. The rod can rotate in vertical plane about the axis at point A. if the car suddenly stops, the angular speed with which the rod starts rotating is
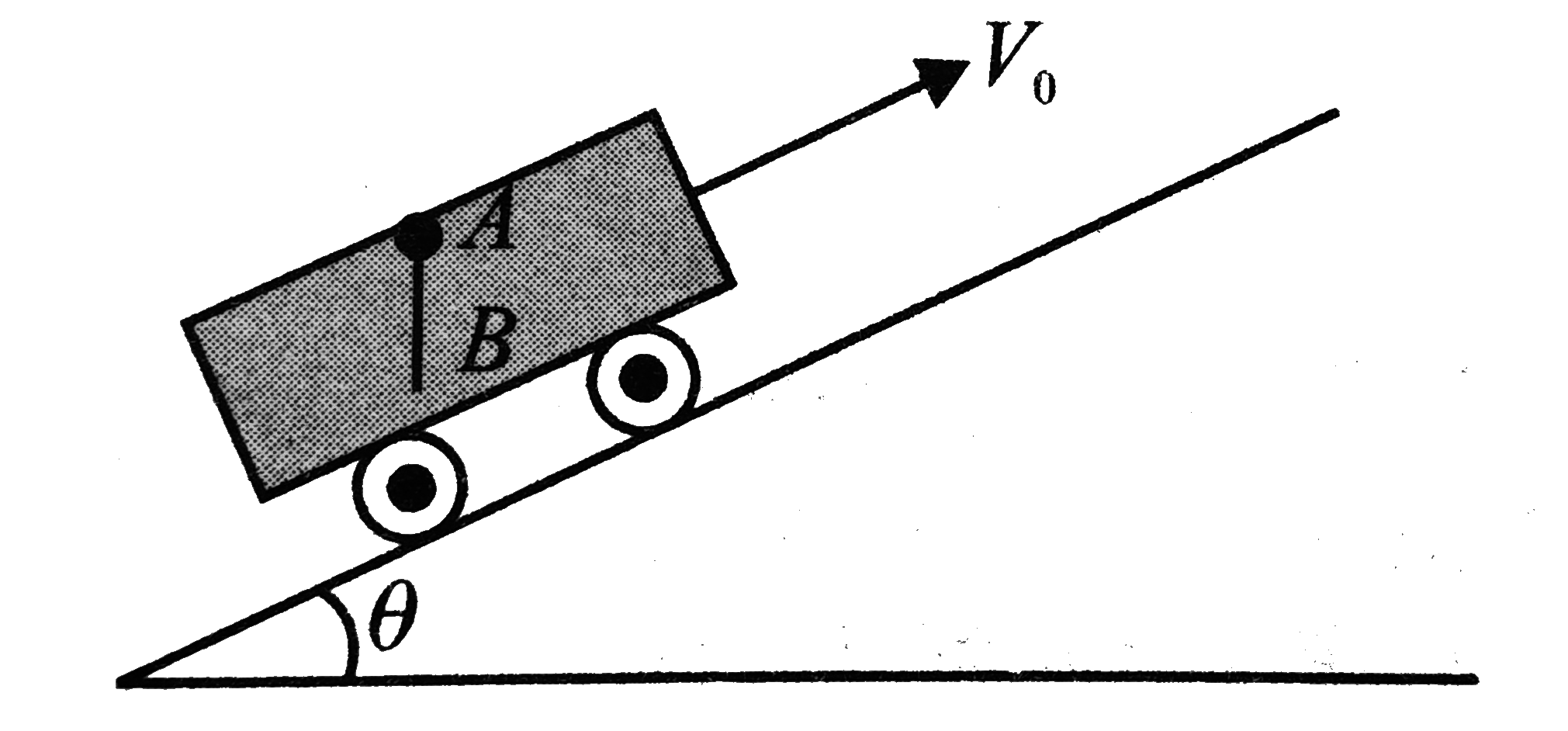 View Solution
View SolutionQuestion 101
A thin plate of mass M,length L and width 2d is mounted vertically on a frictionless fixed axle along the z-axis as shown. Initially, the object is at rest. it is then tapped with a hammer to provide a torque τ, which produces an angular impulse H about the z-axis of magnitude H=∫τdt. What is the angular speed co of the plate about the z-axis after the tap?
 View Solution
View SolutionQuestion 106
A conical pendulum consists of a mass M suspended from a strong sling of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and vˆj velocity. At time t the angular momentum vector of mass M about the point from which the string passes on the ceiling is
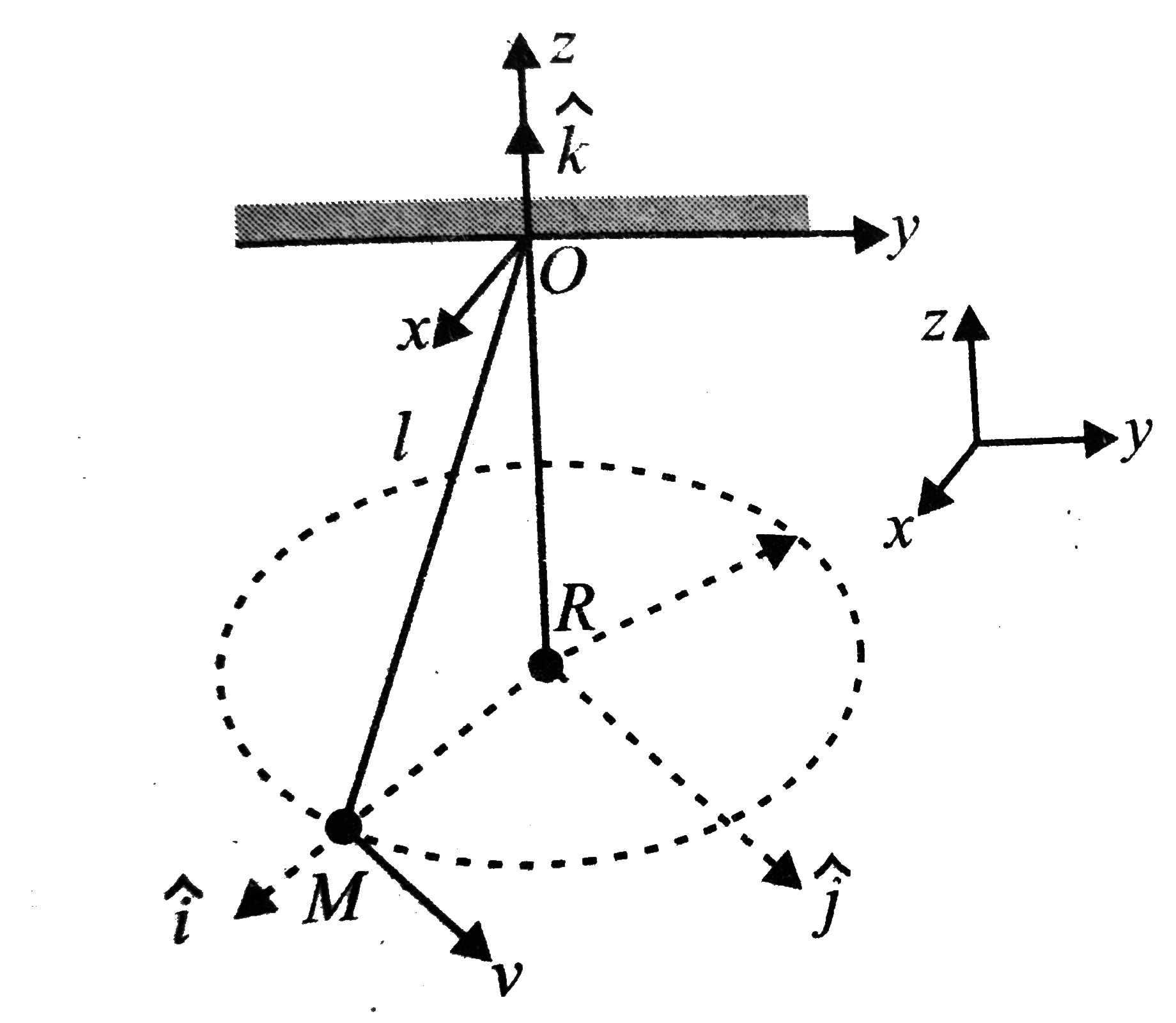 View Solution
View SolutionQuestion 107
A thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
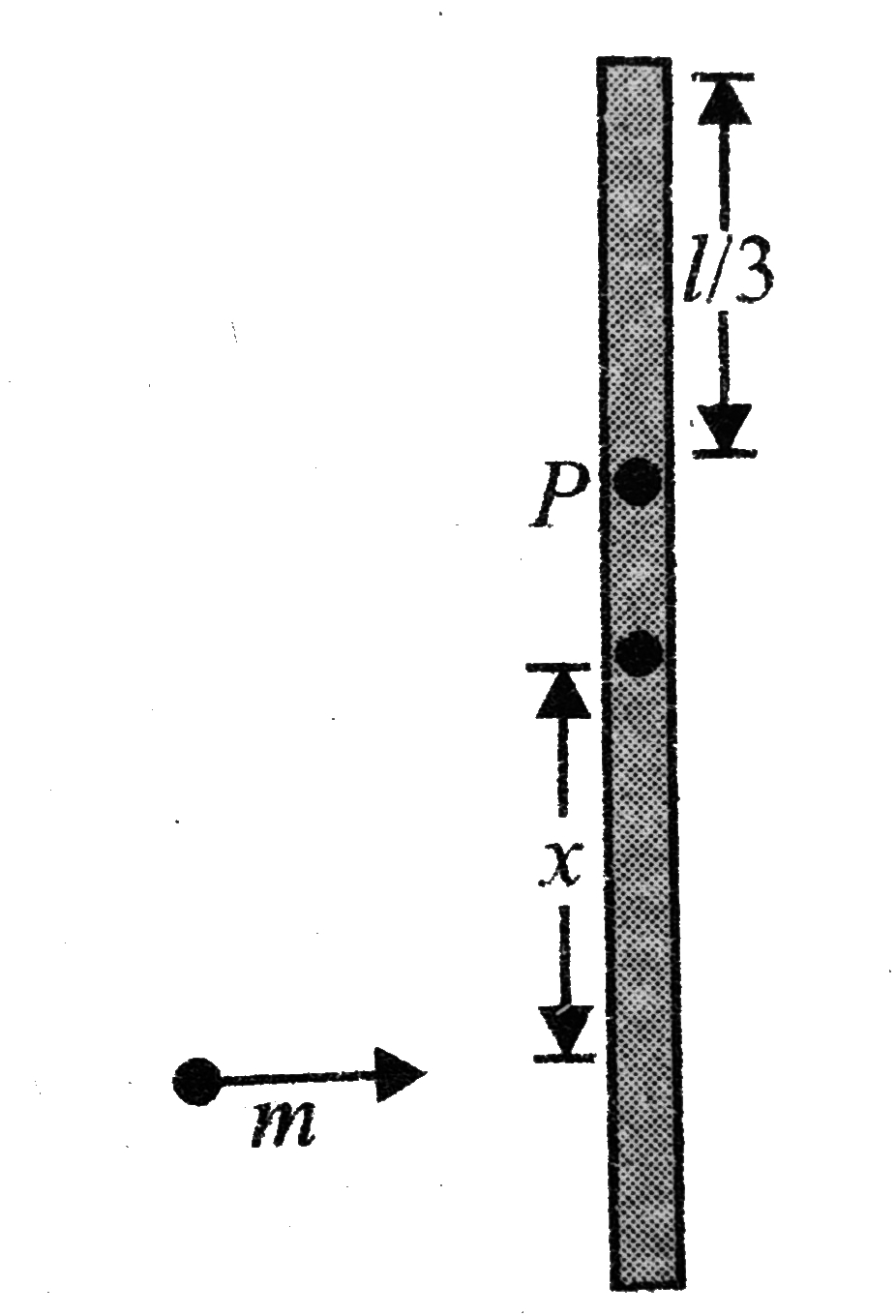 View Solution
View SolutionQuestion 110
A system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are V and 2V, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is
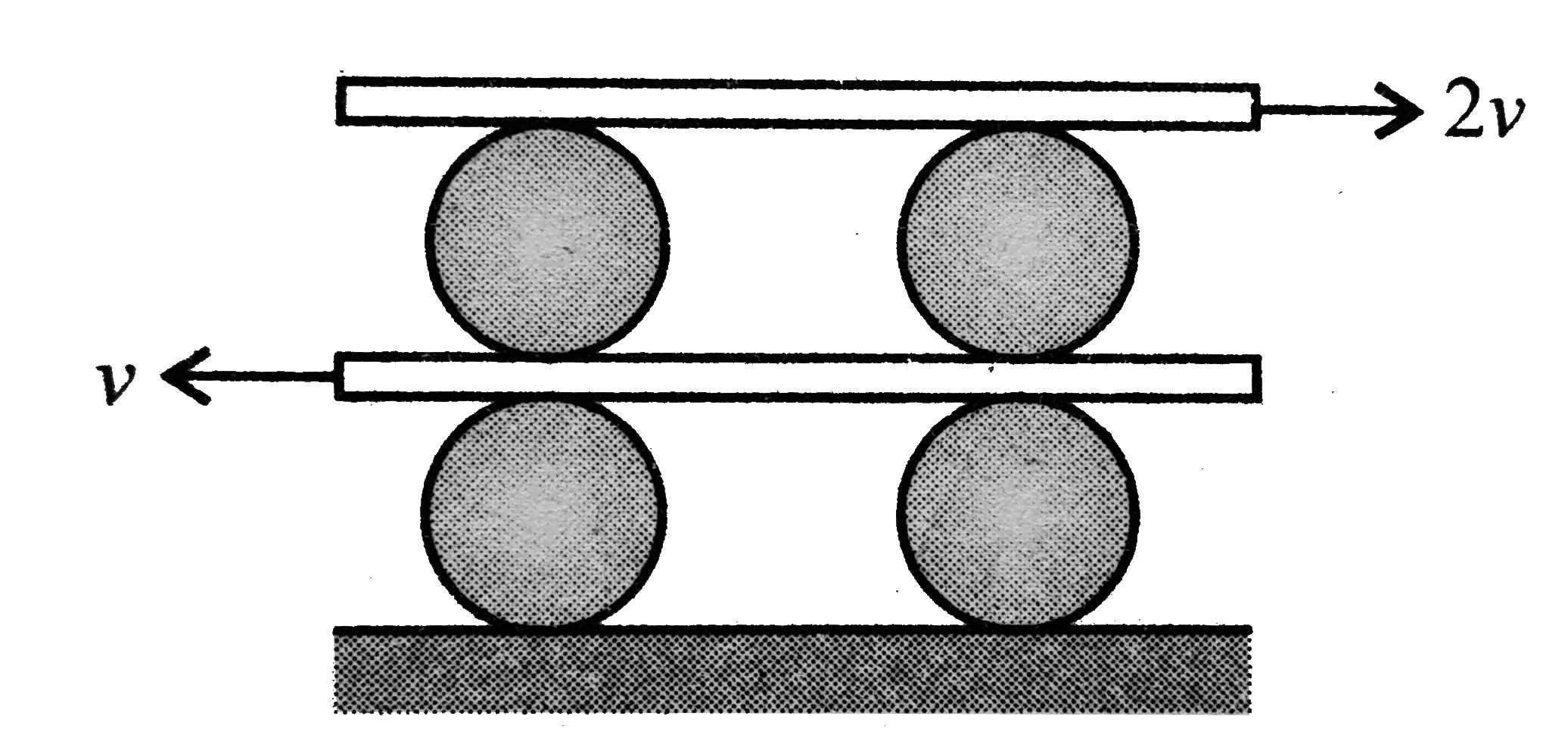 View Solution
View SolutionQuestion 111
The spool shown in the figure is placed on a rough horizontal surface and has inner radius r and outer radius R. The angle θ between the applied force and the horizontal can be varied. The critical angle θ for which the spool does not roll and remains stationary is given by
 View Solution
View SolutionQuestion 112
A small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 View Solution
View SolutionQuestion 113
A block of mass m is attached to a pulley disc of equal mass, radius r by means of a slack string as shown. The pulley is hinged about its centre on a horizontal table and the block is projected with an initial velocity of 5m/s. Find the velocity when the string becomes taut.
 .View Solution
.View SolutionQuestion 114
A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
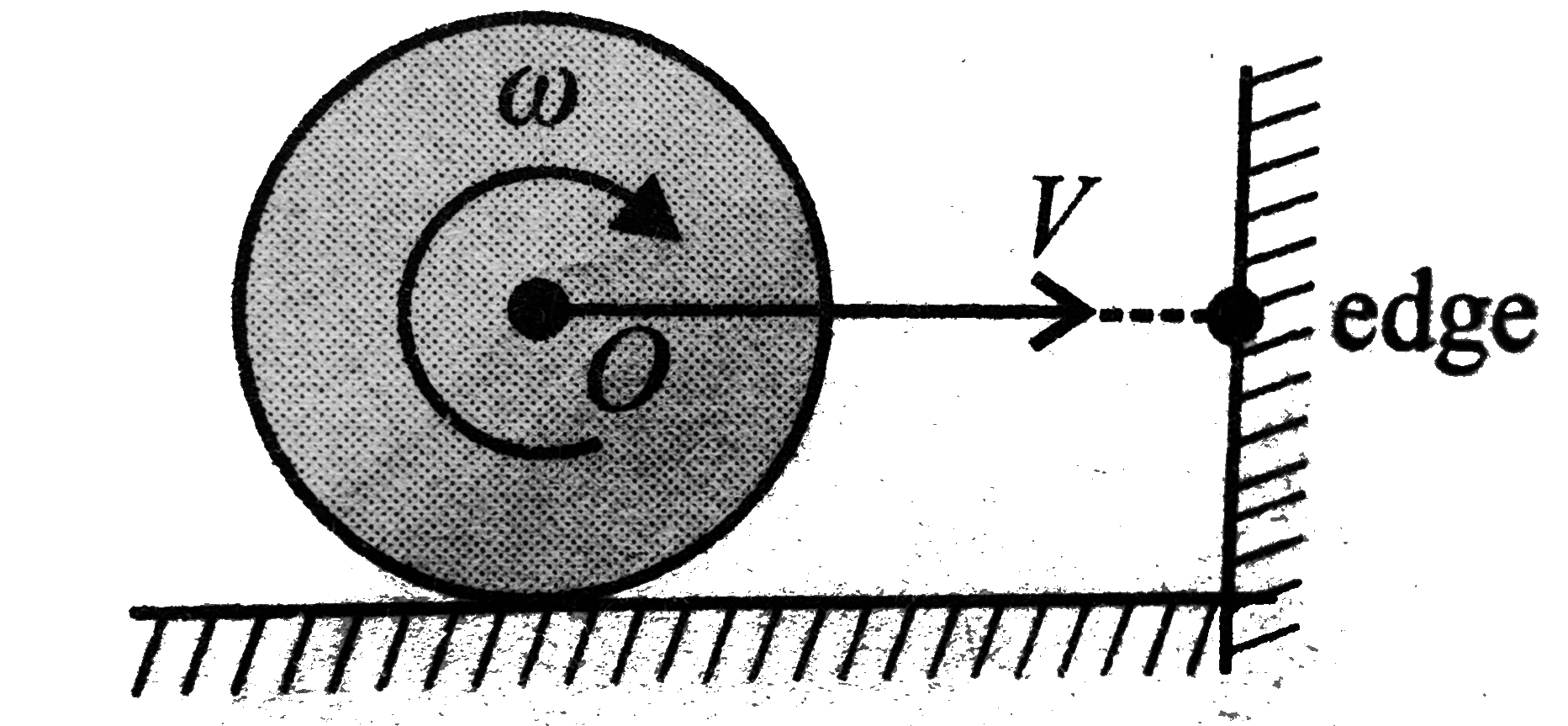 View Solution
View SolutionQuestion 115
A uniform flag pole of length L and mass M in pivoted on the ground with a frictionless hinge. The flag pole makes an angle θ with the horizontal. The moment of inertia of the flag pole about one end is (1/3)ML2. If starts falling from the position shown in figure, the linear acceleration of the free end of the flag pole-labeled P - would be.
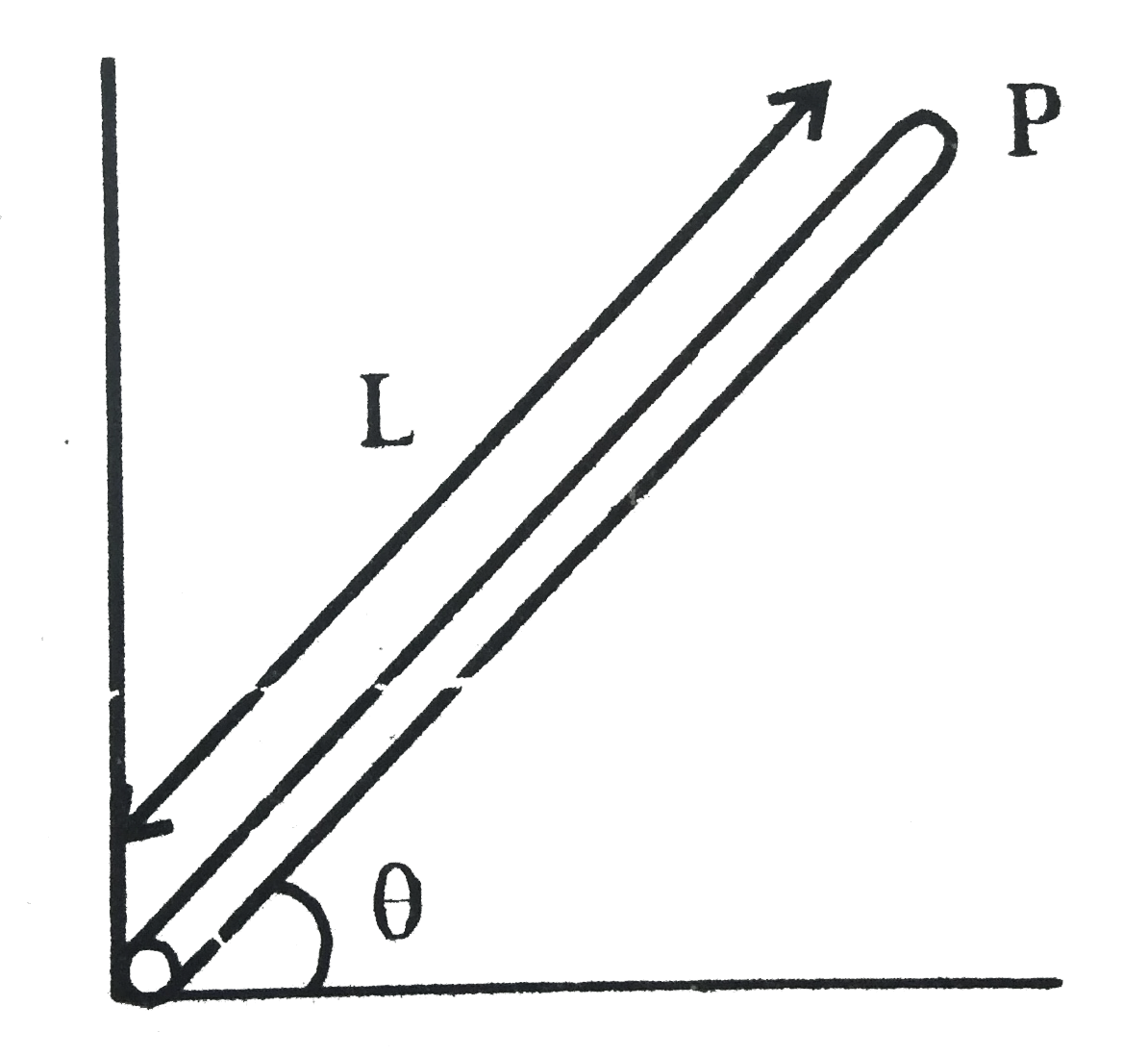 .View Solution
.View SolutionQuestion 125
A uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is it by a particle (mass m) moving on the floor, at a distance l4 from one end elastically (e=1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be View SolutionQuestion 126
A soldi sphere a hollow sphere and a disc, all haing same mass and radius are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom byView SolutionQuestion 127
A uniform rod of mass m and length l is placed over a smooth horizontal surface along the y-axis and is at rest as shown in Fig. An impulsive force F is applied for a small time △t along x-direction at point A. The x-coordinate of end A of the rod when the rod becomes parallel to x-axis for the first time is [initially, the coordinate of centre of mass of the rod is (0,0)]
 View Solution
View SolutionQuestion 128
A mass m is moving at speed v perpendicular to a rod of length d and mass M=6m pivots around a frictionless axle running through its centre and stickes to the end of the rod. The moment of inertia od the rod about its centre is Md2/12. Then the angular speed of the system right after the collision us -View SolutionQuestion 130
A ball of mass moving with constant velocity u collides with a smooth horizontal surface at O as shown in Fig. Neglect gravity and friction. The y-axis is drawn normal to the horizontal surface at the point of impact O and x-axis is horizontal as shown. About which point will the angular momentum of ball be conserved?
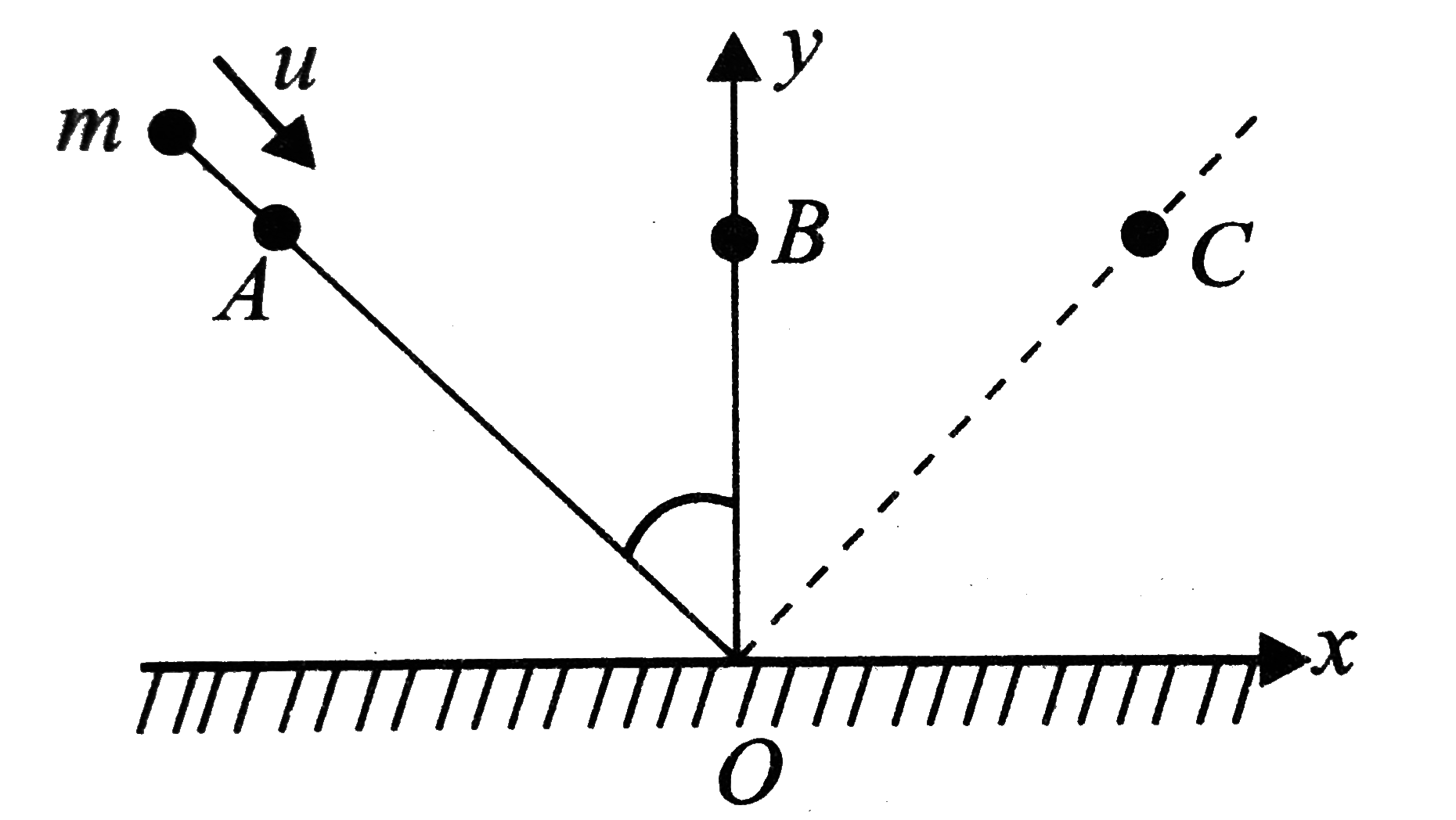 View Solution
View SolutionQuestion 136
A cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................View SolutionQuestion 138
A solid cylinder is placed on the end of an inclined plane. It is found that the plane can be tipped at an angle θ before the cylinder starts to slide. When the cylinder turns on its sides and is allowed to roll, it is found that the steepest angle at which the cylinder performs pure rolling is ϕ. The ratio tanϕ/tanθ isView SolutionQuestion 139
A uniform box of height 2m and having a square base of side 1m, weight 150kg, is kept on one end on the floor of a truck. The maximum speed with which the truck can round a curve of radius 20m without causing the block to tip over is (assume that friction is sufficient is no sliding).View SolutionQuestion 142
Two identical small balls, each of mass m, are connected by a massless and inextensible string of length l and placed on a smooth horizontal xy plane. An external agent pulling the string from its mid-point along y-axis with velocity v0 as shown in Fig. When the separation between the two balls reduces to l/2 then the speed of each ball will be
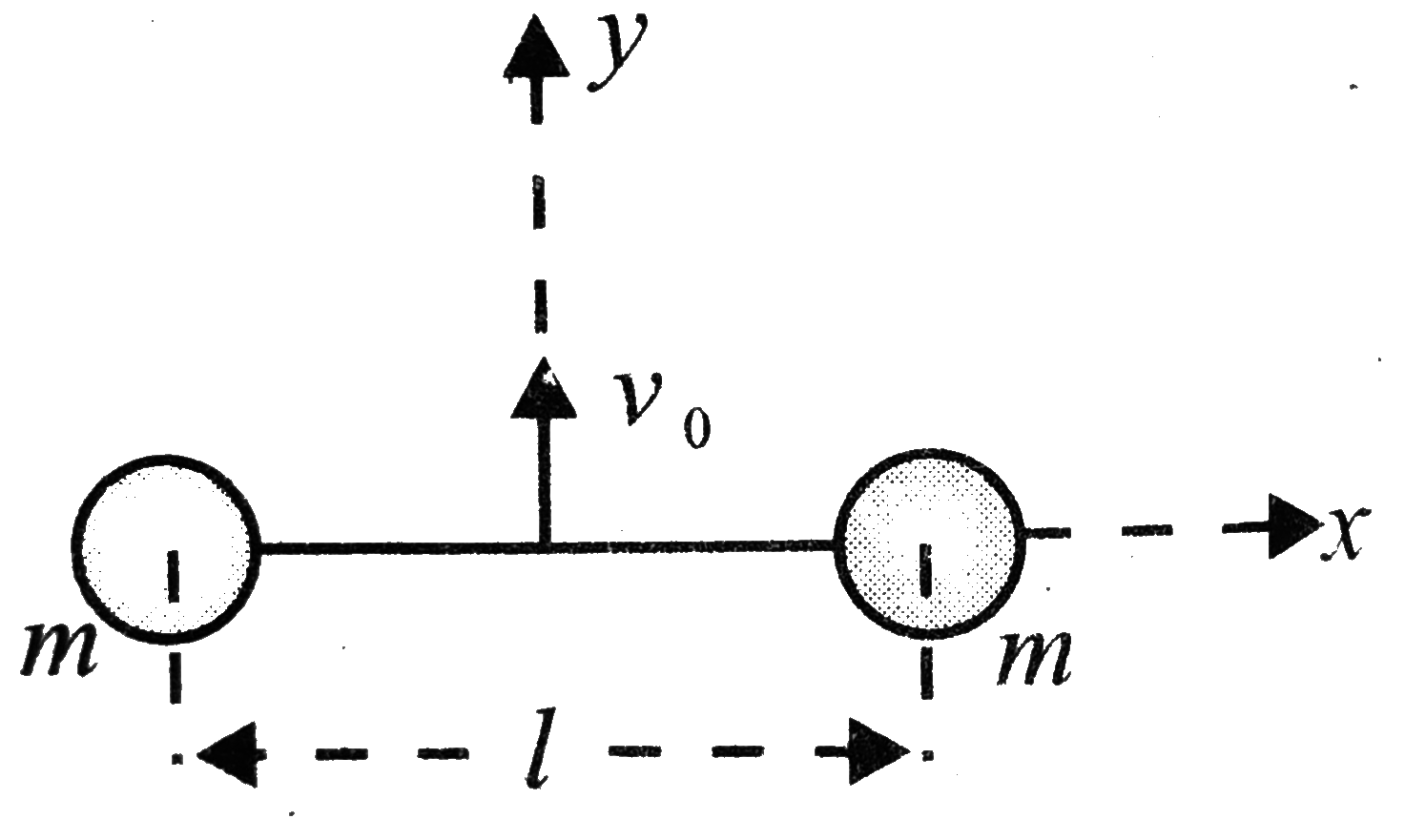 View Solution
View SolutionQuestion 144
A thick walled hollow sphere has outer radius R. It down an inclined plane without slipping and its -speed the bottom is v. If the inclined plane is frictionless and the sphere slides down without rolling, its speed at the bottom 5v/4. What is the radius of gyration of the sphere?View SolutionQuestion 145
A uniform disk turns at 2.4rev/s around a frictionless axis. A nonrotating rod, of the same mass as the disk and length equal to the disk's diameter is dropped onto the freely spinning disk (see the figure). They then both turn around the axis with their centres superposed. What will be the angular frequency in rev/s of the combination when they start rotating together.
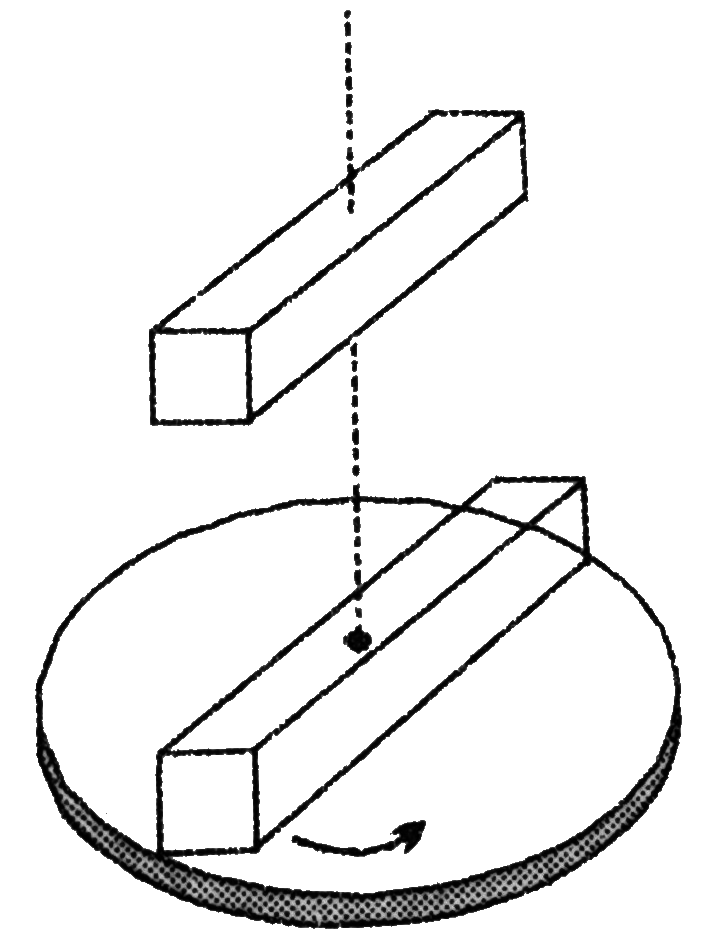 View Solution
View SolutionQuestion 147
Suppose you are standing on the edge of a spinning platform and step off at right angles to the edge (radially outward). Now consider it the other way. You are standing on the ground next to a spinning carousel and you step onto the platform at right angles to the edge (radially inward). View SolutionQuestion 150
A uniform solid sphere rolls up (witout slipping) the fixed inclined plane, and then back down. Which is the correct graph of acceleration a of centre of mass of solid sphere as function of time t (for the duration sphere is on the incline)? Assume that the sphere rolling up has a positive velocity.
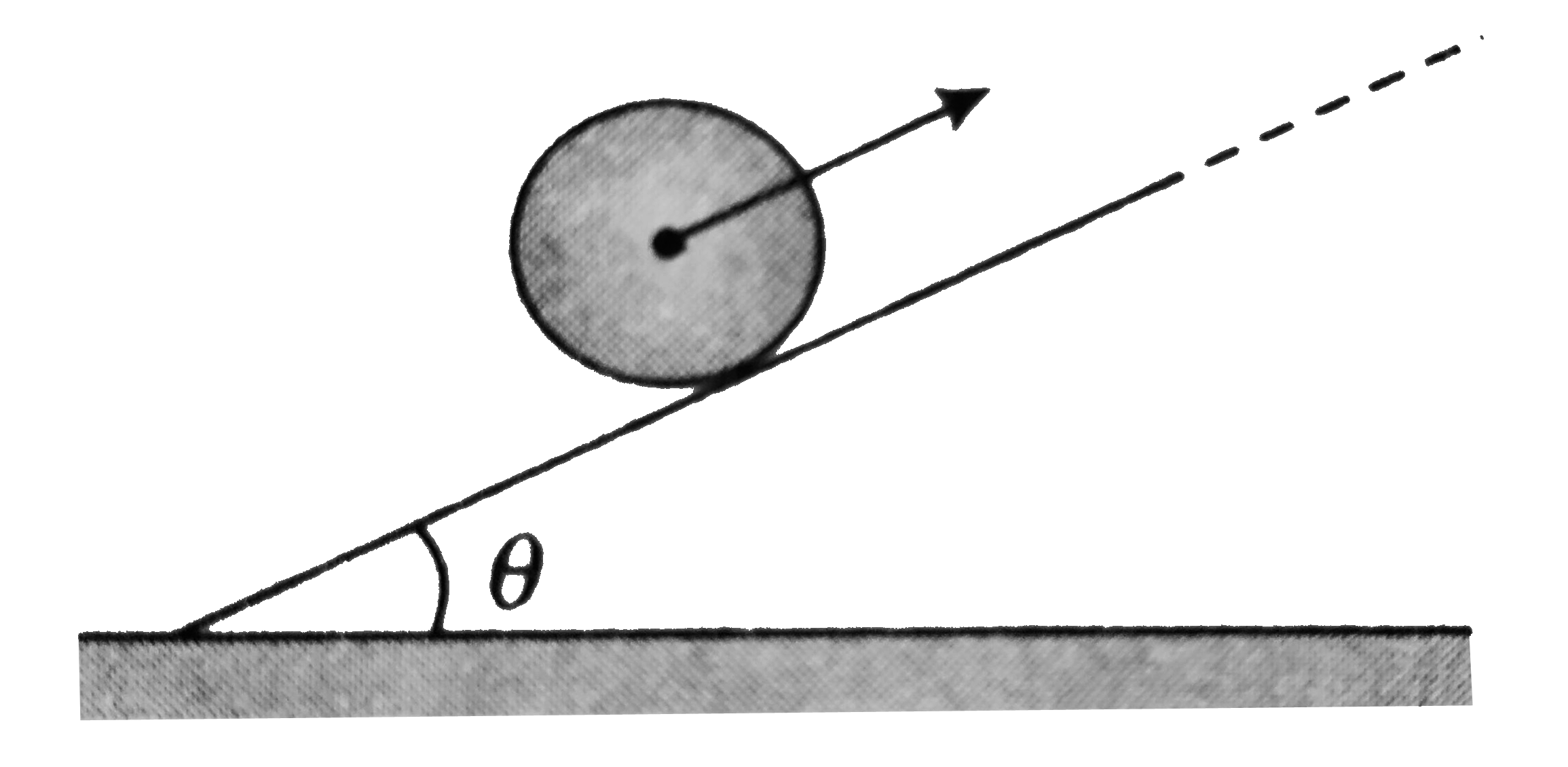 View Solution
View SolutionQuestion 151
A conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
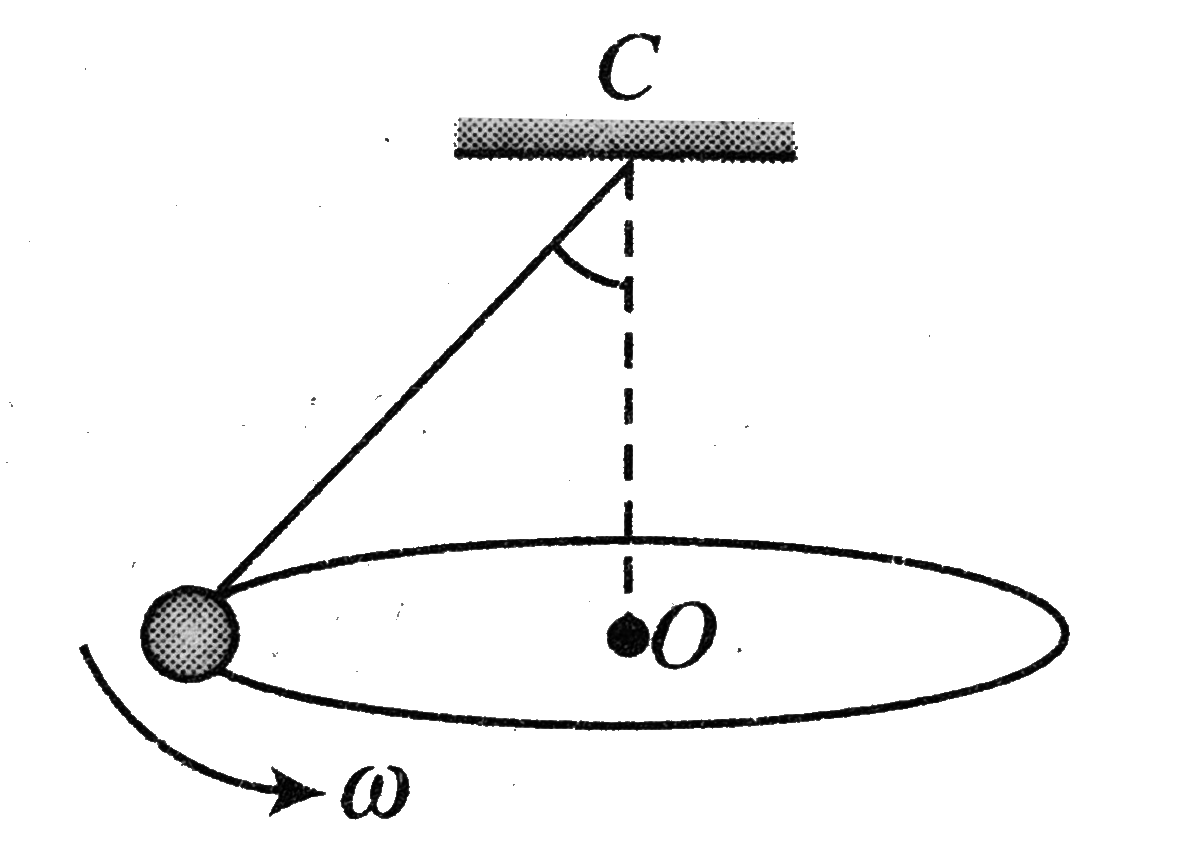 View Solution
View SolutionQuestion 152

A child with mass m is standing at the edge of a merry go round having moment of inertia I, radius R and initial angular velocity ω as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity v with respect to the ground. The new angular velocity of the merry go round isView SolutionQuestion 153
Two identical uniform solid spherical balls A and B of mass m each are placed on a the fixed wedge as shown in figure. Ball B is kept at rest and it is released just before two balls collides. Ball A rolls down without slipping on inclined plane and collide elastically with ball B. The kinetic energy of ball A just after the collision with ball B is:
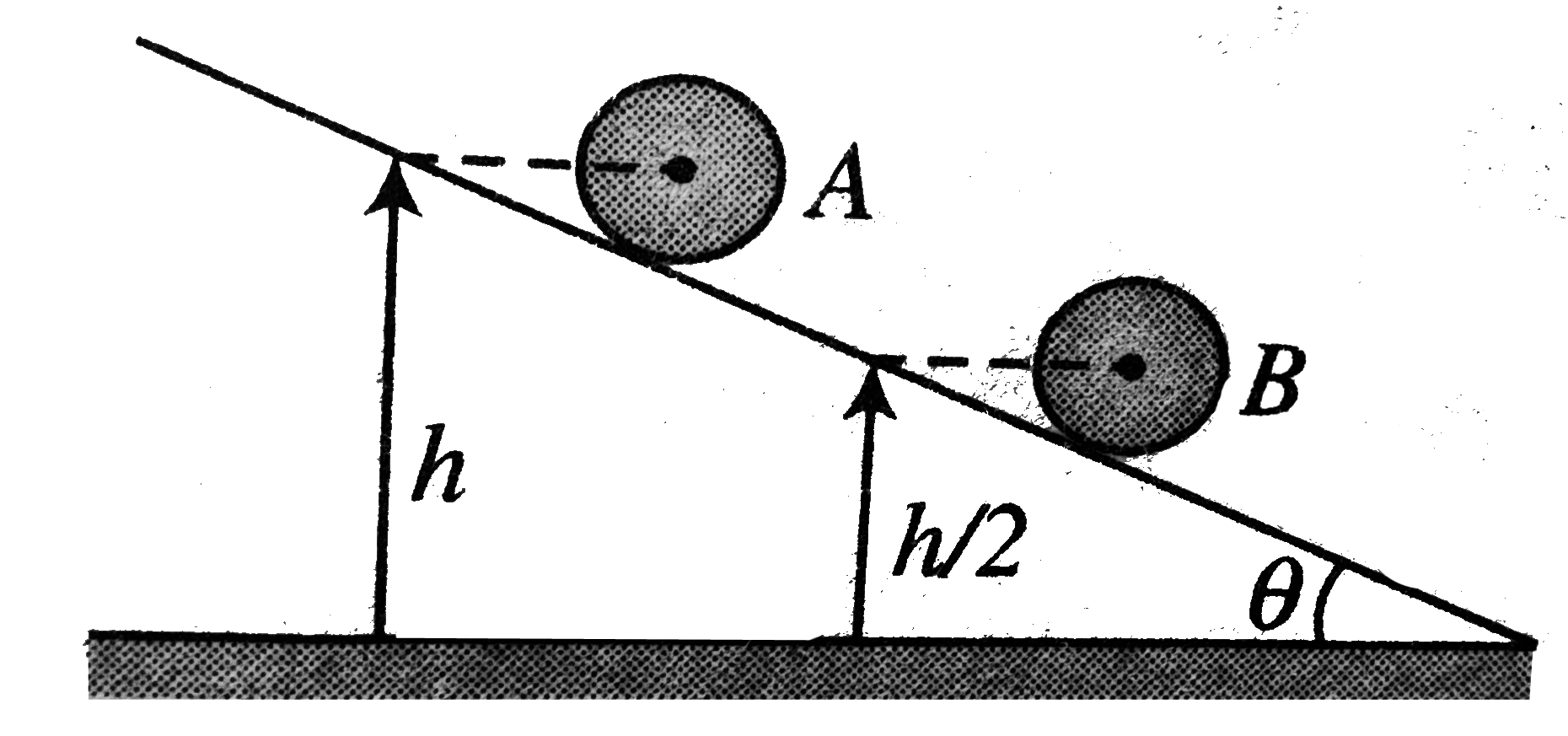 View Solution
View SolutionQuestion 154
In both the figures all other factors are same, except that in figure (i) AB is rough and BC is smooth while in figure (ii) AB is smooth and BC is rough. In figure (i), if a sphere is released from rest it starts rolling. Now consider the figure (ii), if same sphere is A released from top of the inclined plane, what will be the kinetic energy of the sphere on reaching the bottom:
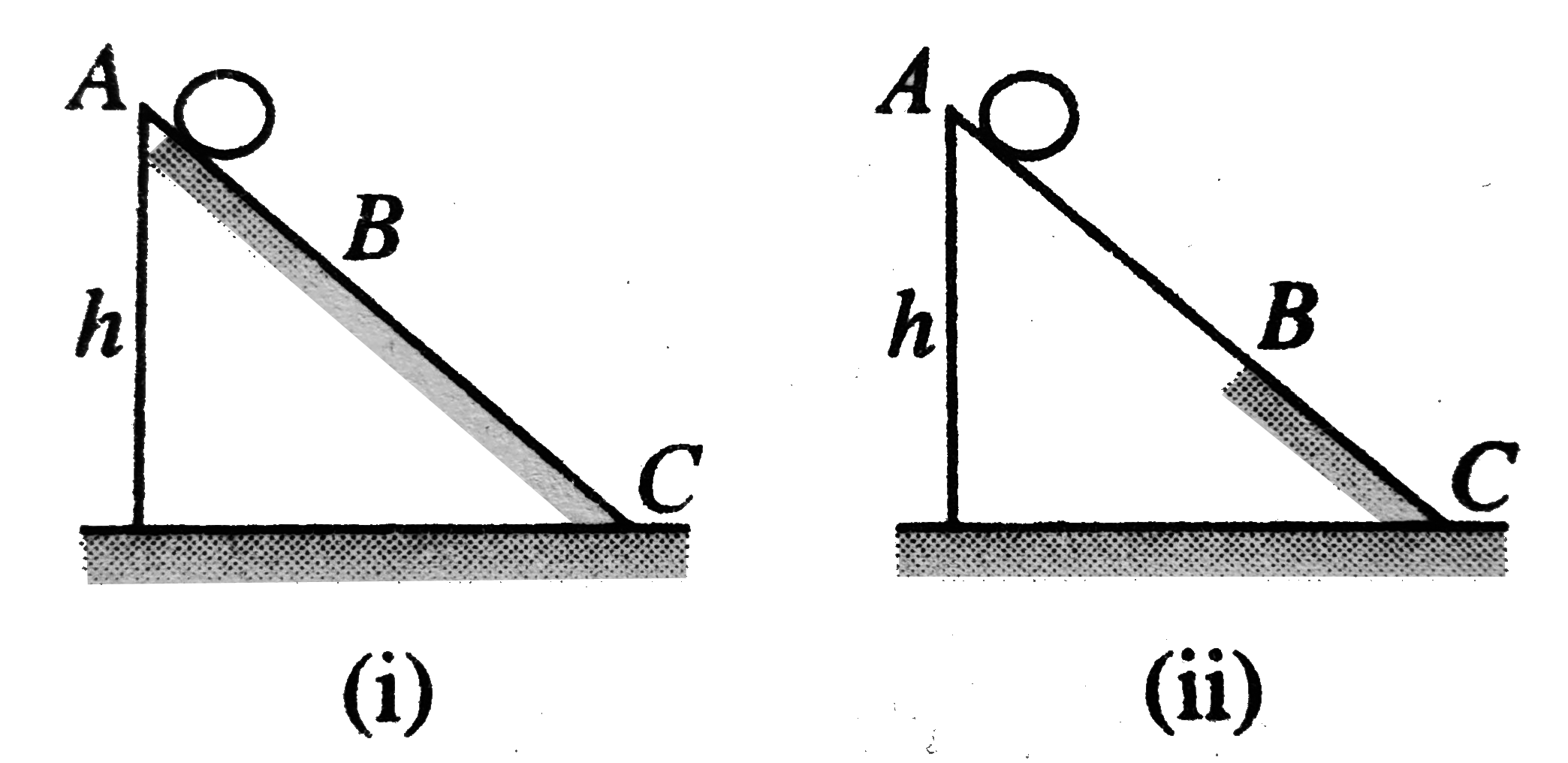 View Solution
View SolutionQuestion 156
A homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0, then: View SolutionQuestion 159
Three identical solid spheres move down three incline A,B and C are all of the same dimensions. A is without friction, the friction between B and a sphere is sufficient to cause rolling without slipping, the friction between C and a sphere causes rolling with slipping. The kinetic energies, of A,B,C at the bottom of the inclines are EA,EB,EC.View SolutionQuestion 166
A small stone of mass m is attached to a light string which passes through a hollow tube. The tube is held by one hand and the free end of the string by the other hand. The mass is set into revolution in a horizontal circle of radius r1 with a speed v1 . The string is pulled down shortening the radius of the circular path to r2. Which of the following is not correct? (ω1 and T have usual meanings) View SolutionQuestion 170
Two cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
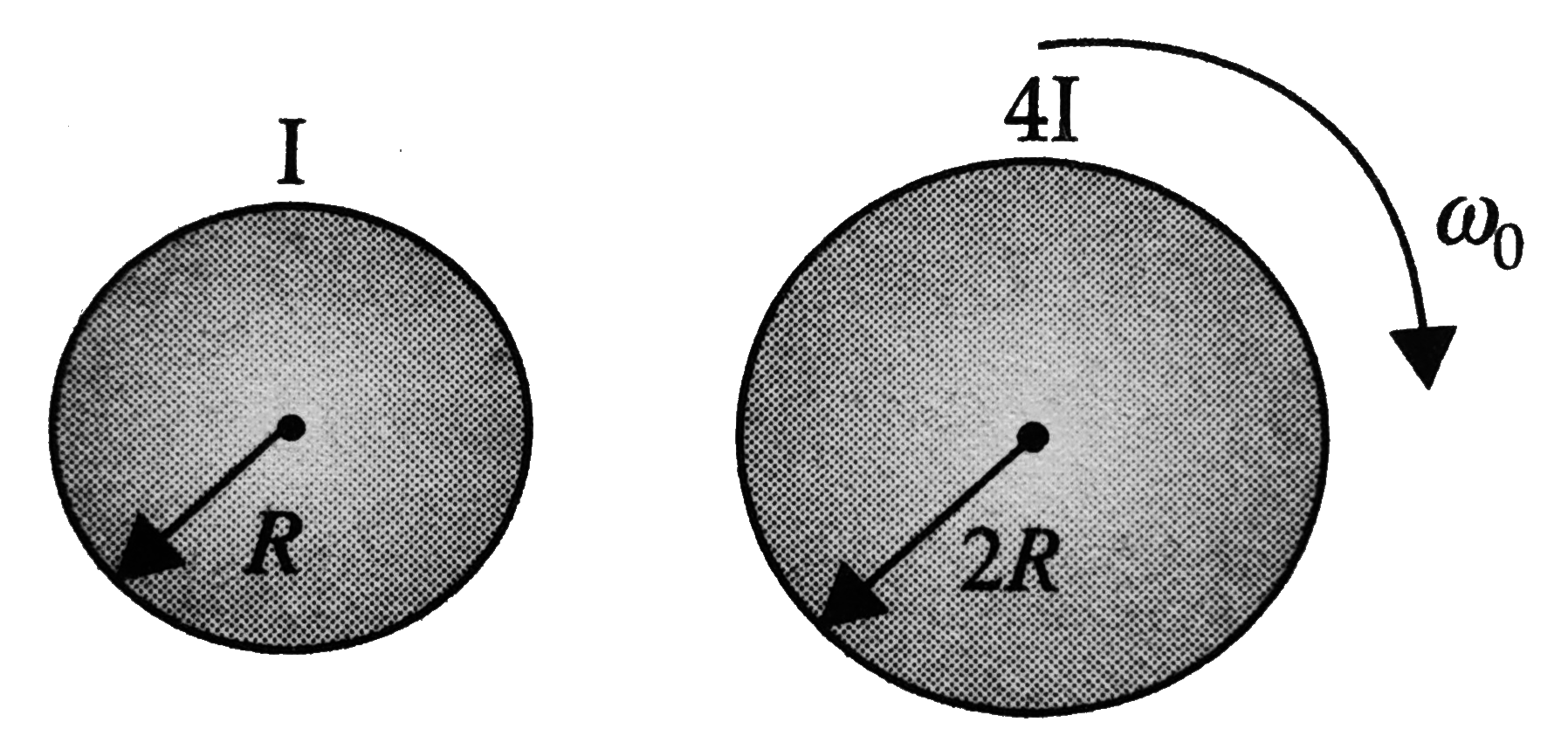 View Solution
View SolutionQuestion 172
In the figure shown mass of both, the spherical body and block is m. Moment of inertia of the spherical body about centre of mass is 2mR2. The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
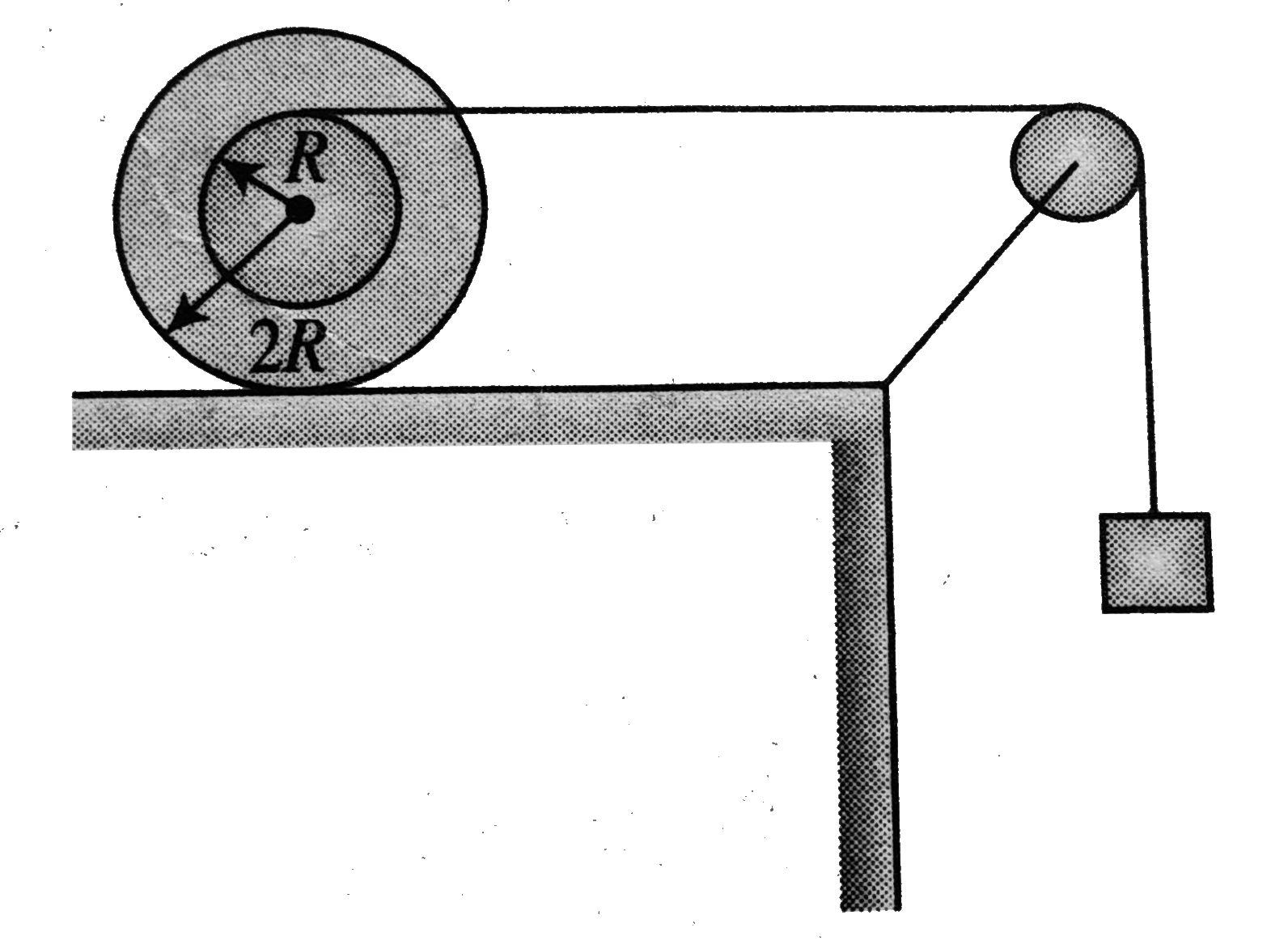 View Solution
View SolutionQuestion 173
A cylinder executes pure rolling without slipping with a constant velocity on a plank, whose upper surface is rough enough, but lower surface is smooth. The plank is kept at rest on a smooth horizontal surface by the application of an external force F. Choose the correct alternative:
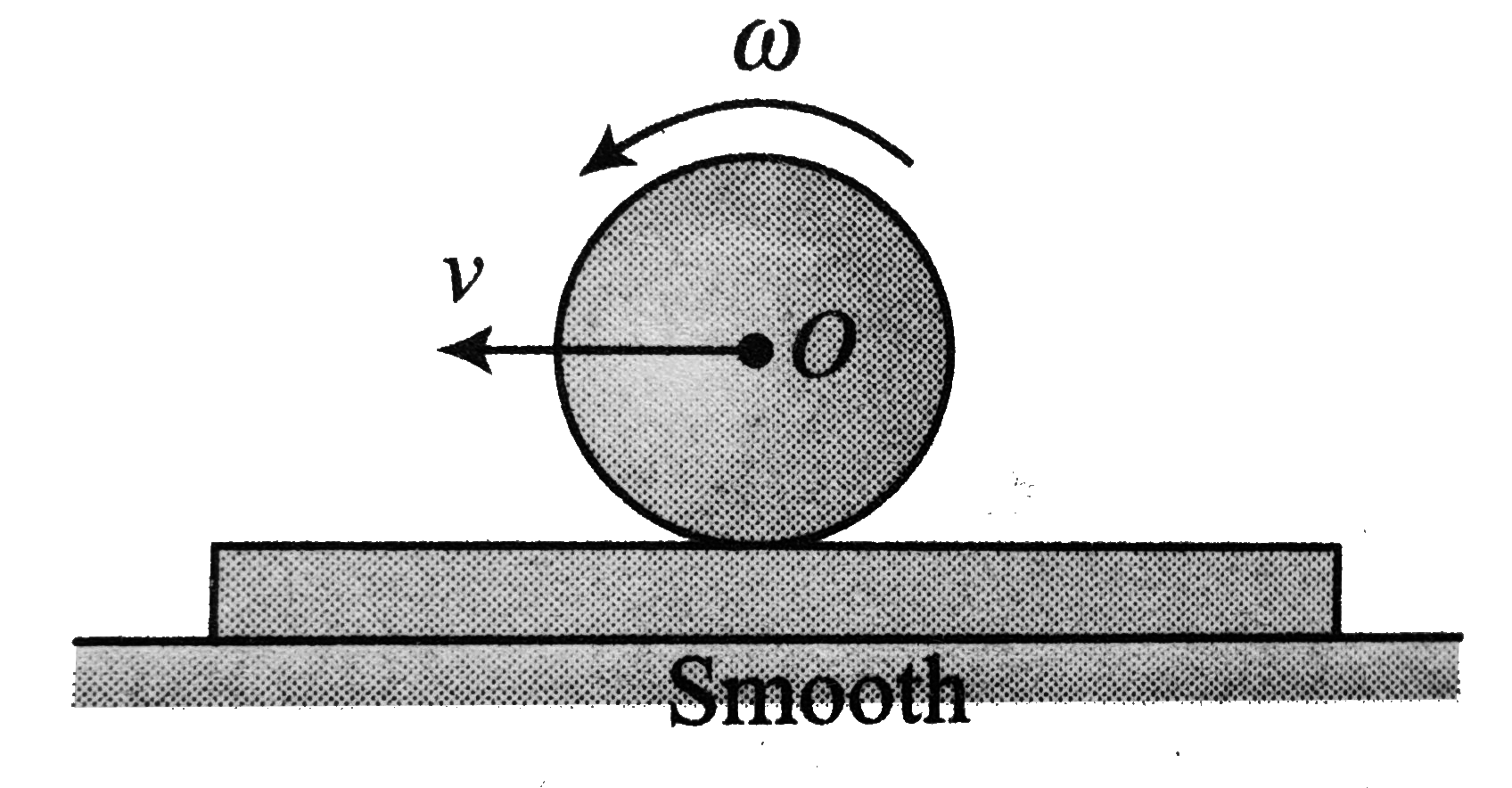 View Solution
View SolutionQuestion 176
Two rigid bodies A and B rotate with angular momenta LA and LB respectively. The moments of inertia of A and B about the axes of rotation are IA and IB respectively. If IA=IB/4 and LA=5LB, then the ratio of rotational kinetic energy KA of A to the rotational kinetic energy KB of B is given by View SolutionQuestion 178
A boy stands over the centre of a horizontal platform which is rotating freely with a speed of 2revolutions/s about a vertical axis through the centre of the platform and straight up through the boy. He holds 2kg masses in each of his hands close to his body. The combined moment of inertia of the system is 1kg×metre2. The boy now stretches his arms so as to hold the masses far from his body. In this situation, the moment of inertia of the system increases to 2kg×metre2, The kinetic energy of the system in the latter case as compared with that in the previous case willView SolutionQuestion 184
A horizontal turn table in the form of a disc of radius r carries a gun at G and rotates with angular velocity ω0 about a vertical axis passing through the centre O. The increase in angular velocity of the system if the gun fires a bullet of mass m with a tangential velocity v with respect to the gun is (moment of inertia of gun + table about O is I0
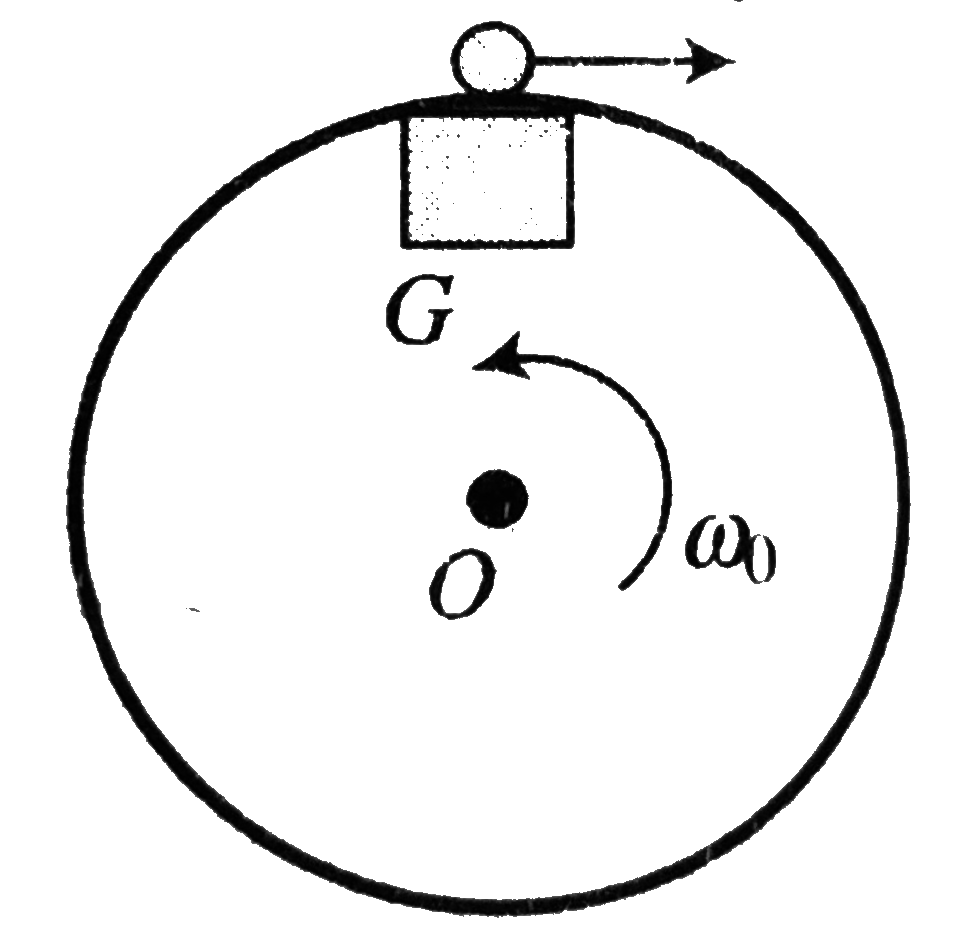 View Solution
View SolutionQuestion 185
A circular platform is mounted on a vertical frictionless axle. Its radius is r=2m and its moment of inertiaI=200kgm2. It is initially at rest. A 70kg man stands on the edge of the platform and begins to walk along the edge at speed v0=1ms−1 relative to the ground. The angular velocity of the platform is.View SolutionQuestion 195
Consider three uniform solid spheres. sphere (i ) has radius r and mass m sphere (ii) has radius r and mass 3m, sphere (iii) has radius 3r and mass 'm'. All the spheres can be placed at the same point on the same inclined plane where they will roll without slipping to the bottom. If allowed to roll down the incline, then at the 'bottom of the incline View SolutionQuestion 202
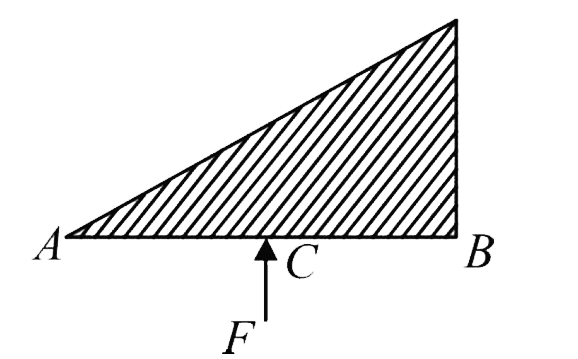
A disc of circumference s is at rest at a point A on a horizontal surface when a constant horizontal force begins to act on its centre. Between A and B there is sufficient friction toprevent slipping, and the surface is smooth to the right of B.AB=s. The disc moves from A to B in time T. To the right of B,
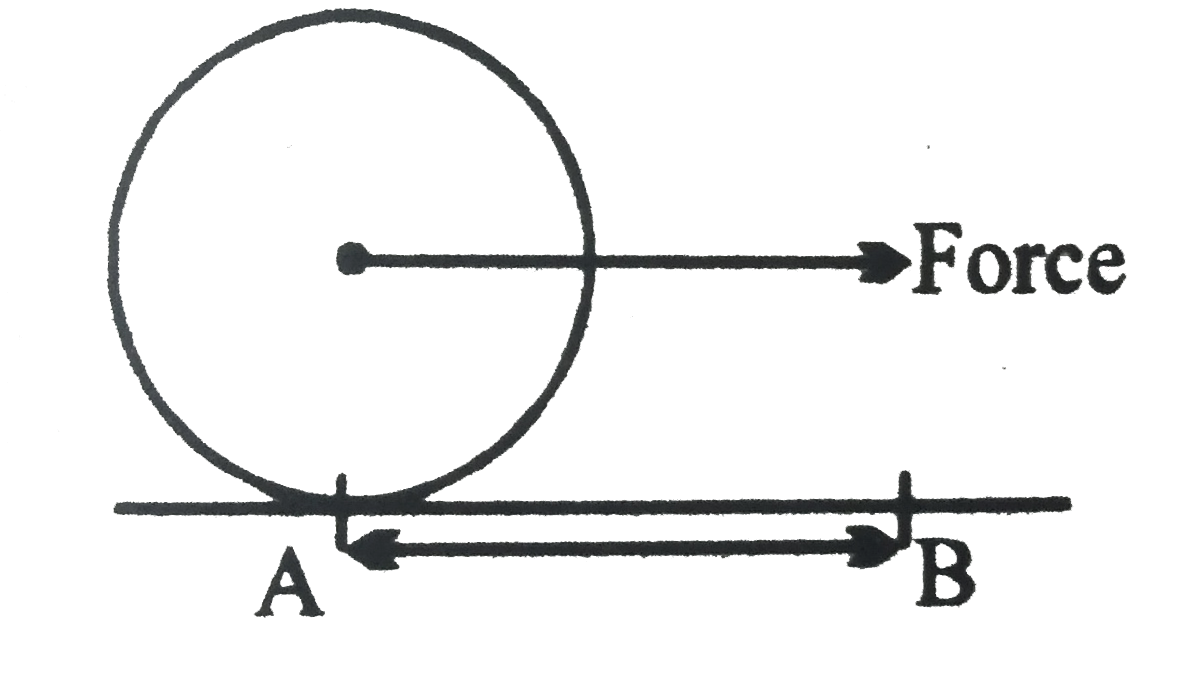 .View Solution
.View SolutionQuestion 208
A horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in Fig. The particle initially rest on a horizontal plane. A horizontal velocity v0 is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements:
 View Solution
View SolutionQuestion 210
A ball rolls down an inclined plane and acquires a velocity vr when it reaches the bottom of the plane. If the same ball slides without friction and acquires rolling from the same height down an equally inclined smooth plane and acquires a velocity vs (then which of the following statements are not correct?View SolutionQuestion 216
A uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then
 View Solution
View SolutionQuestion 221
A uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis, passing through the centre of the disc. A piece of disc from its rim detaches itself from the disc at the instant when it is, on the same horizontal with the centre of the disc and moving upwards. lien about the fixed axis, the angular speed of theView SolutionQuestion 225
The motion of a sphere moving on a rough horizontal surface changes from pure sliding (without rolling) to pure rolling (without slipping). In this process, the force of friction
(i) intially acts opposite to the direction of motion and late in the direction of motion
(ii) cause linear retardation
(iii) causes angular acceleration
(iv) stops acting when pure rolling beginsView SolutionQuestion 228
Figure shows a spool with thread wound on it placed on a smooth plane inclined at angle from horizontal. The spool has mass m, edge radius R, and is wound up to a radius r. its moment of inertia about its own axis is I. The free end of the thread is attached as shown in the figure. So that the thread is parallel to the inclined plane. T is the tension in the thread. Which of the following is correct?
 View Solution
View SolutionQuestion 231
A stepped cylinder having mass 50kg and a radius of gyration (K) of 0.30m. The radii R1 and R2 are respectively 0.3m and 0.6m. A pull T equal to 200N is exerted on the rope attached to inner cylinder. The coefficient of static and dynamic friction between cylinder and ground are 0.1 and 0.08 respectively.
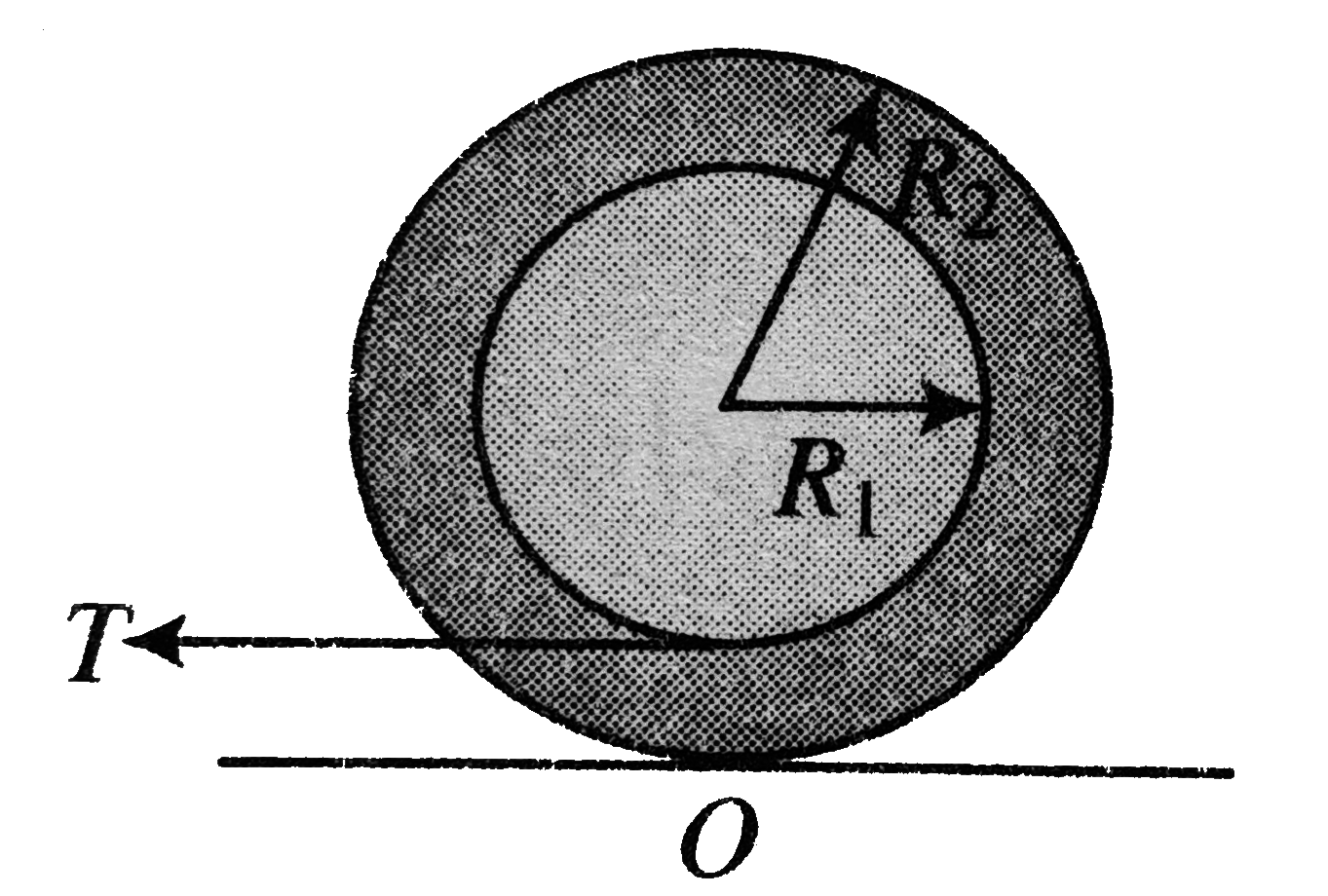 View Solution
View SolutionQuestion 232
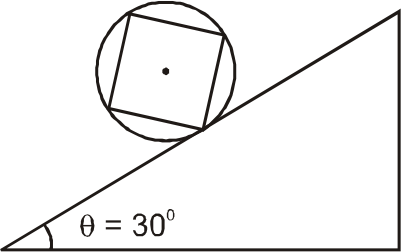
Statement I: A disc is allowed to roll purely on an inclined plane as shown in Fig. A force F parallel to the incline and passing through the centre of the disc acts which remains constant during the motion.
It is possible that for certain values of F, the friction on the disc is acting along downward direction and for certain other values of F, the friction on the disc be acting along upward direction and there is no other possibility.
Statement II: The friction (if acting) will be static and not kinetic in nature. View SolutionQuestion 237
A disc is rolling on an inclined plane without slipping. The velocity of centre of mass is V. These other point on the disc lie on a circular are having same speed as centre of mass.
When a disc is rolling on an inclined plane. The magnitude of velocities of all the point from the contact point is same, having distance equal to radius r.View SolutionQuestion 238

Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The moment of inertia of system about the axis of ring will be-View SolutionQuestion 239
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The acceleration of centre of mass of system isView SolutionQuestion 240
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The minimum value of coefficient of friction to prevent slipping is-View SolutionQuestion 241
Figure shows a uniform smooth solid cylinder A of radius 4m rolling without slipping on the 8kg plank which, in turn, is supported by a fixed smooth surface. Block B is known to accelerate down with 6m/s2 and block C moves down with acceleration 2m/s2.

What is the angular acceleration of the cylinder? View SolutionQuestion 242
Figure shows a uniform smooth solid cylinder A of radius 4m rolling without slipping on the 8kg plank which, in turn, is supported by a fixed smooth surface. Block B is known to accelerate down with 6m/s2 and block C moves down with acceleration 2m/s2.
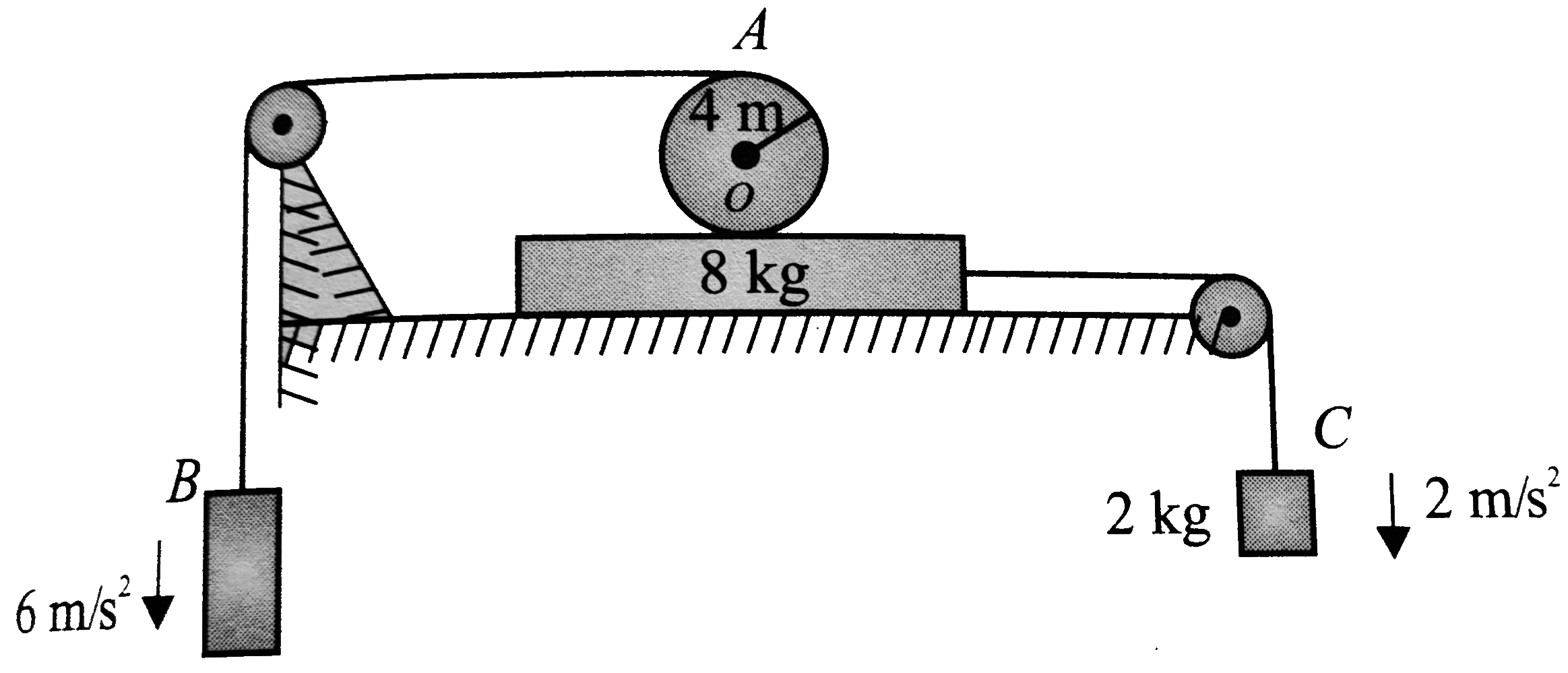
What is the ratio of the mass of the cylinder to the mass of block B? View SolutionQuestion 243
Figure shows a uniform smooth solid cylinder A of radius 4m rolling without slipping on the 8kg plank which, in turn, is supported by a fixed smooth surface. Block B is known to accelerate down with 6m/s2 and block C moves down with acceleration 2m/s2.
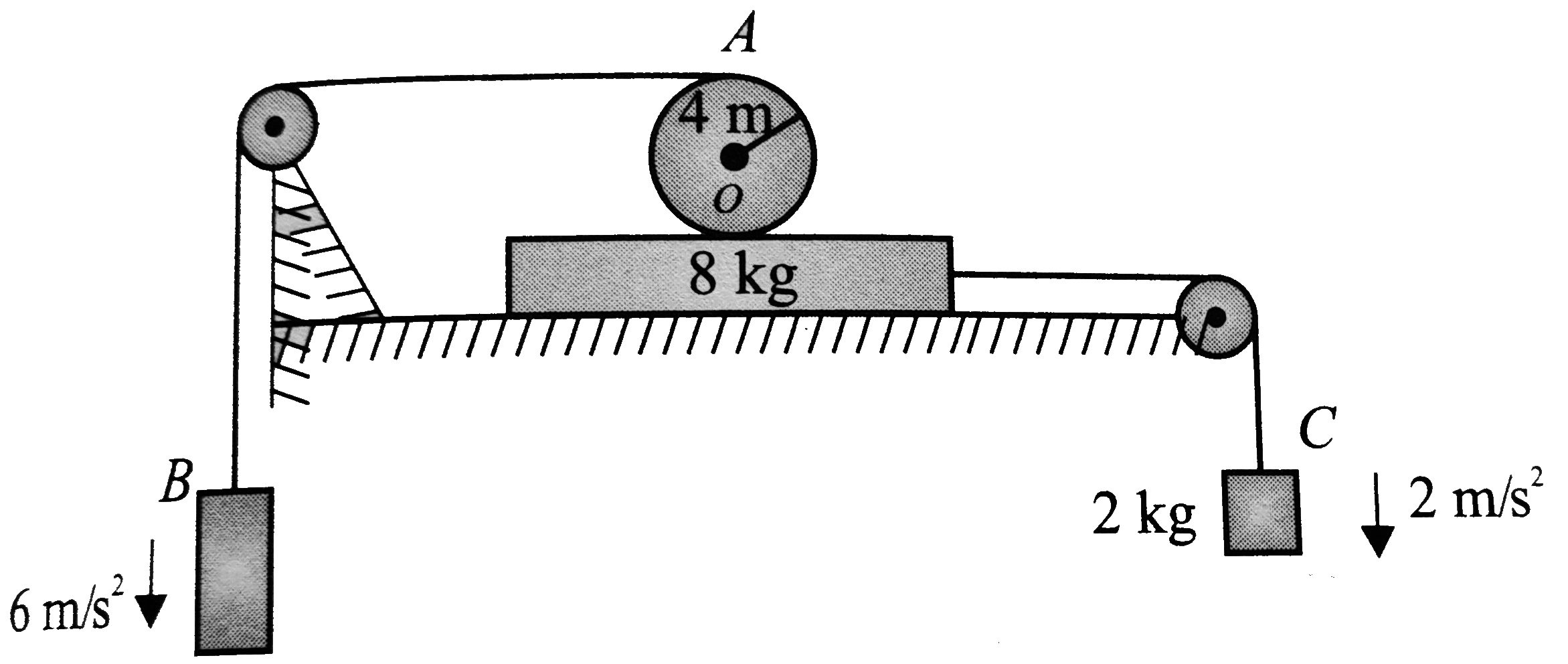
If unwrapped length of the thread between the cylinder and block B is 20m at the beginning, when the system was released from rest, what would it be 2s later View SolutionQuestion 244
A man of mass 100kg stands at the rim of a turtable of radius 2m and moment of inertia 4000kgm2 mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of 1m/s relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?View SolutionQuestion 245
A man of mass 100kg stands at the rim of a turtable of radius 2m and moment of inertia 4000kgm2 mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of 1m/s relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?View SolutionQuestion 246
A man of mass 100kg stands at the rim of a turtable of radius 2m and moment of inertia 4000kgm2 mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of 1m/s relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?View SolutionQuestion 247
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
What will be the radius of the circle when the cord breaks? View SolutionQuestion 248
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
Velocity of the block at the time of breaking of the string View SolutionQuestion 250
A uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision. View SolutionQuestion 252
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
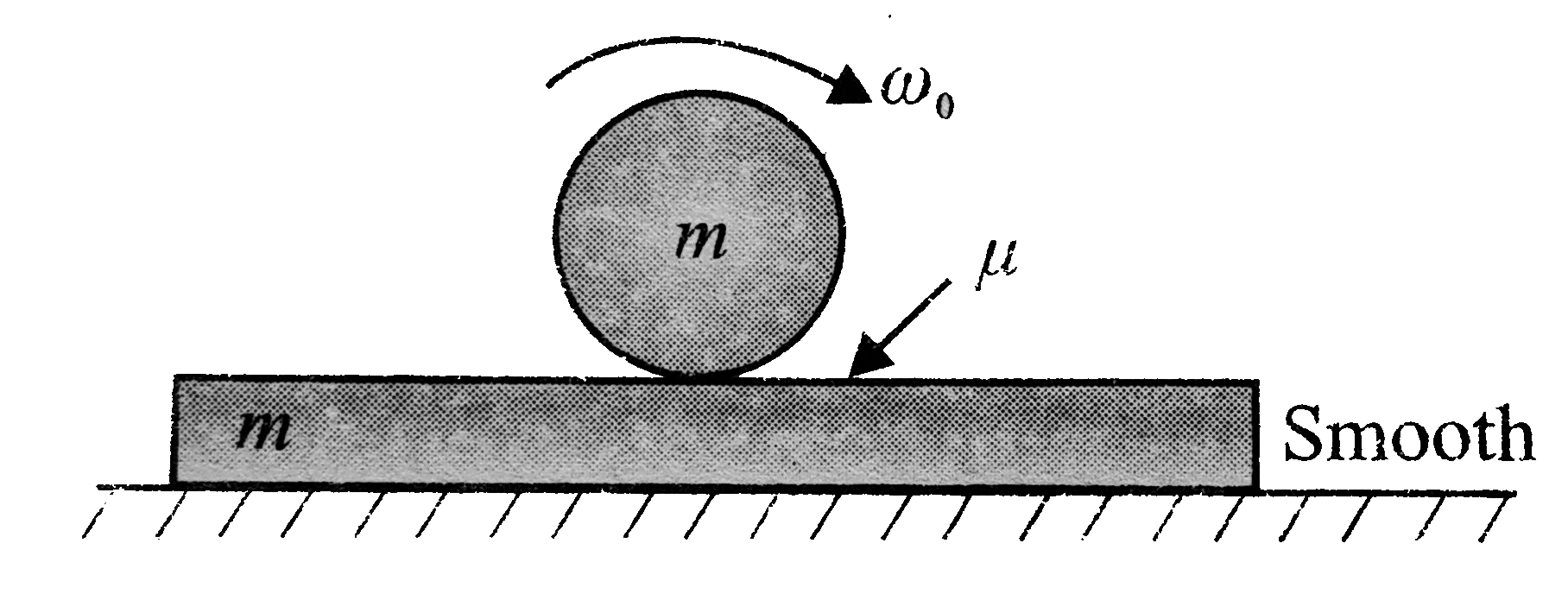
Find the time t at which the pure roiling startsView SolutionQuestion 253
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling startsView SolutionQuestion 254
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.View SolutionQuestion 255
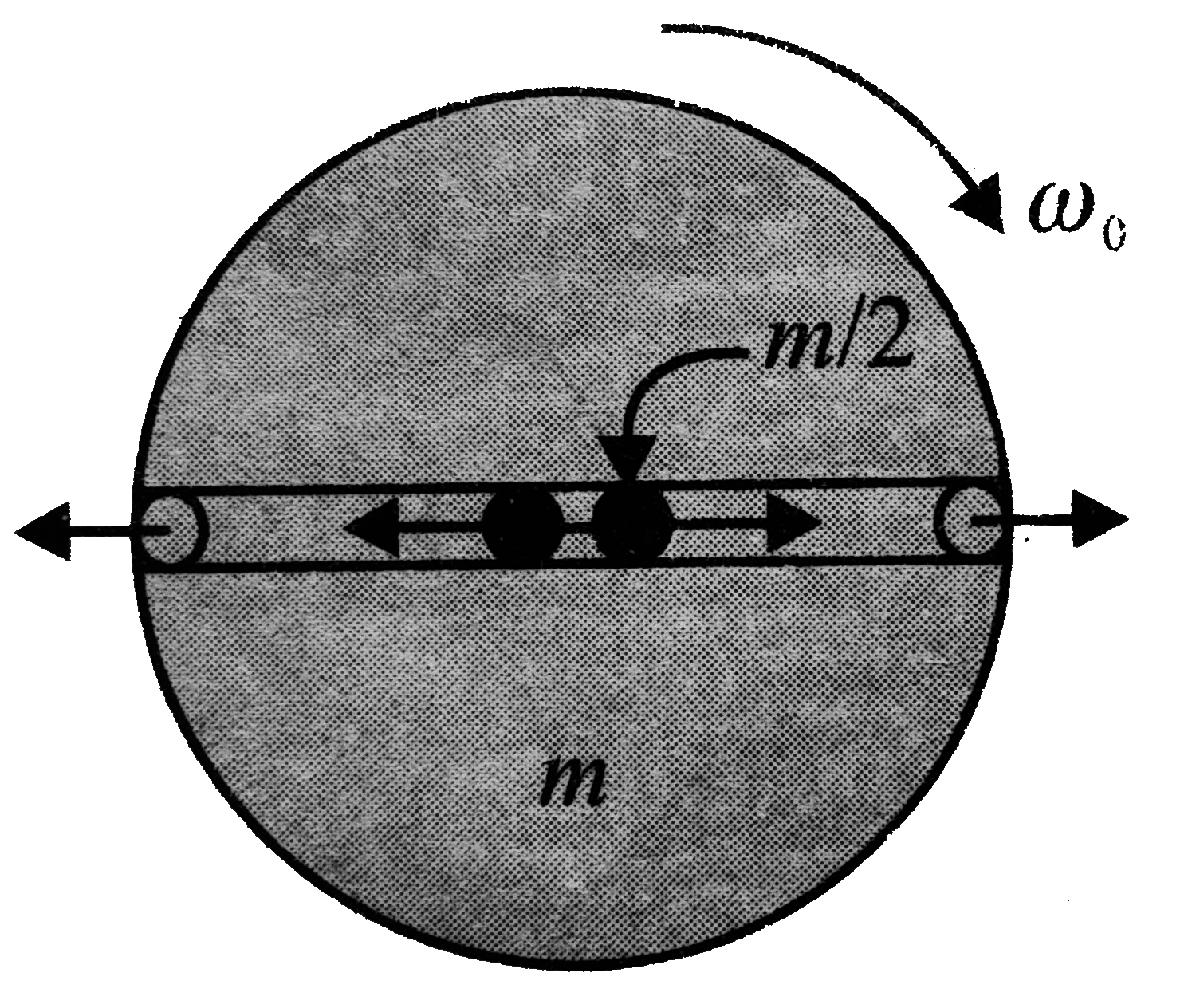
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is View SolutionQuestion 256
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The speed of each ball relative to the ground just after they leave the disc is
 View Solution
View SolutionQuestion 257
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The net work done by forces exerted by the disc on the ball for the duration ball remains on the disc isView SolutionQuestion 258
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.View SolutionQuestion 259
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView SolutionQuestion 260
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collisionView SolutionQuestion 261
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the angular momentum of the particle and of then about the centre of mass C before the collision. View SolutionQuestion 262
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision. View SolutionQuestion 263
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track is View SolutionQuestion 264
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
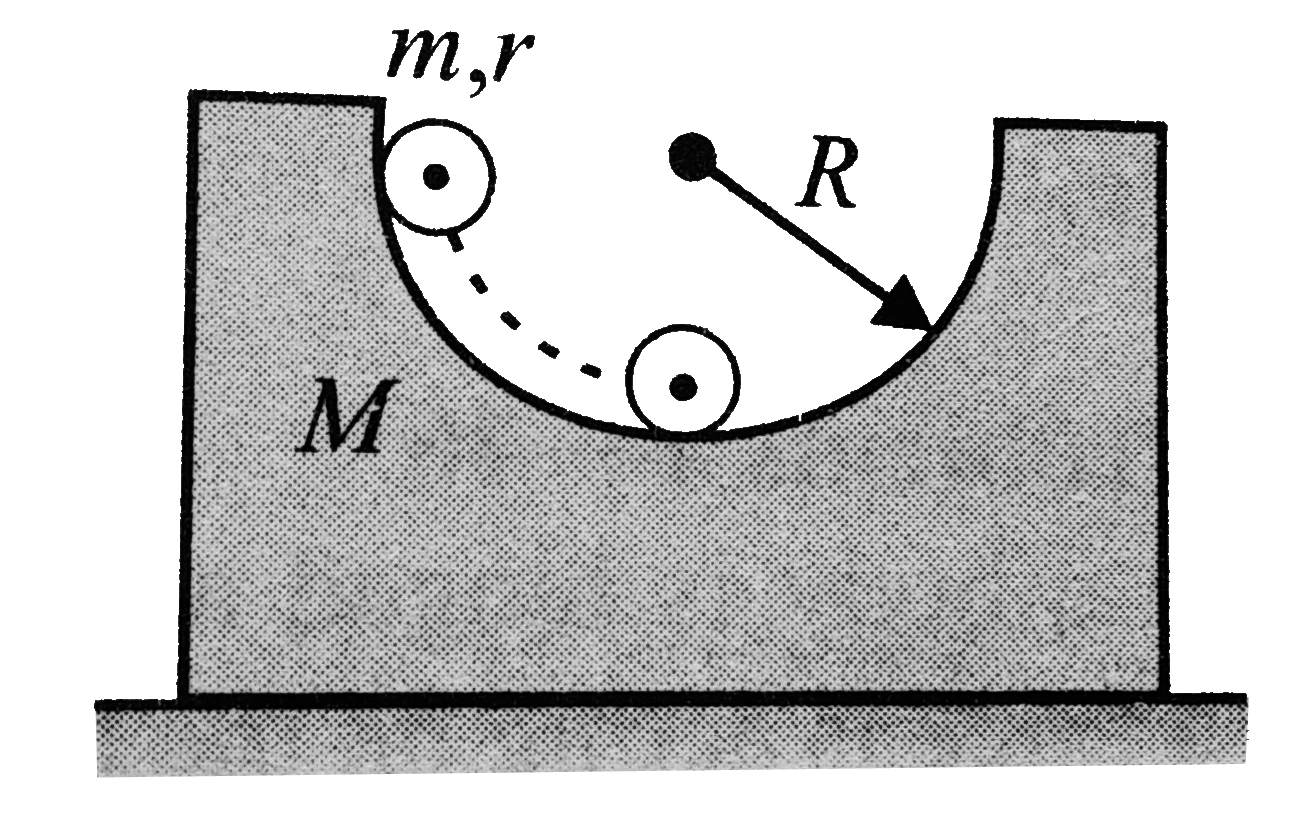
The speed of the cylinder when it reaches the bottom of the track is View SolutionQuestion 265
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
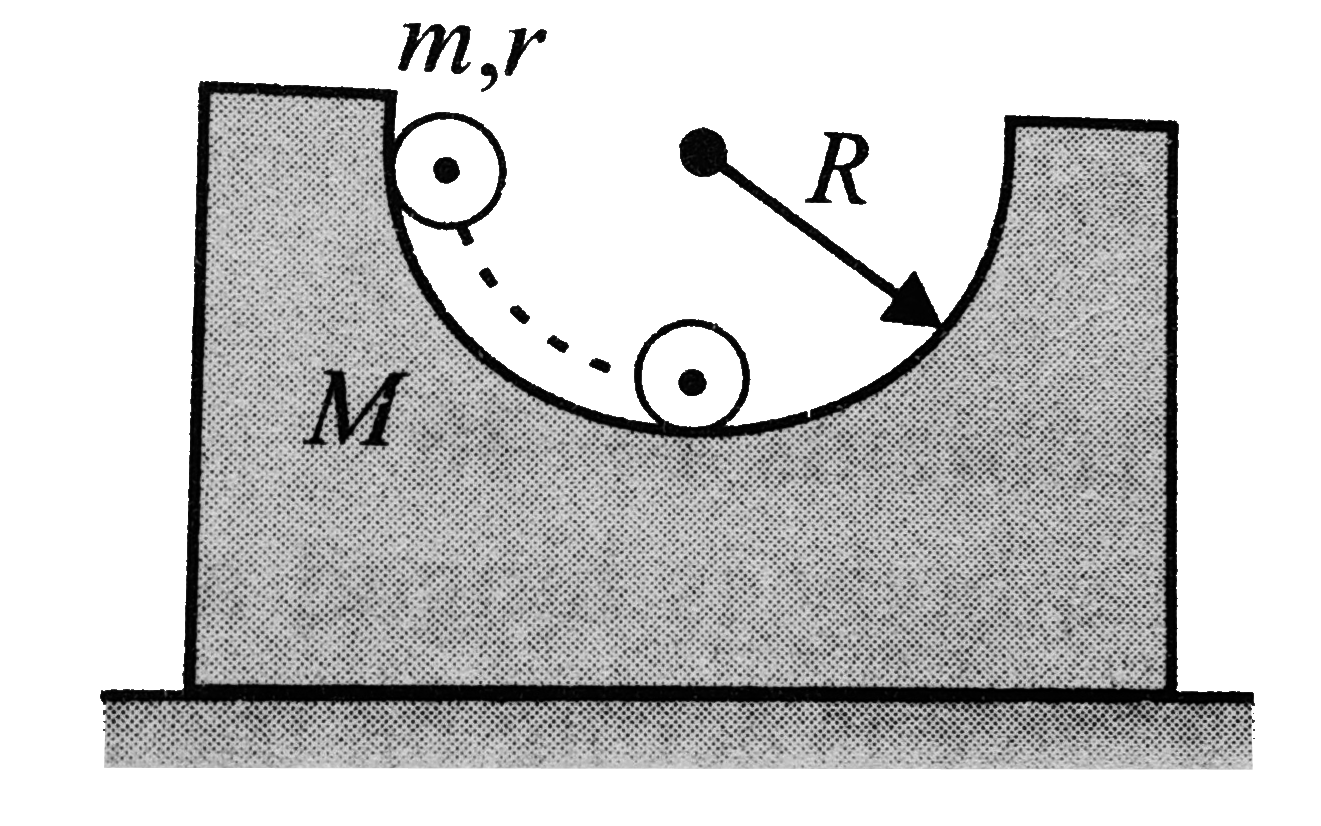
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is View SolutionQuestion 266
A disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the center of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ isView SolutionQuestion 267
A disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information
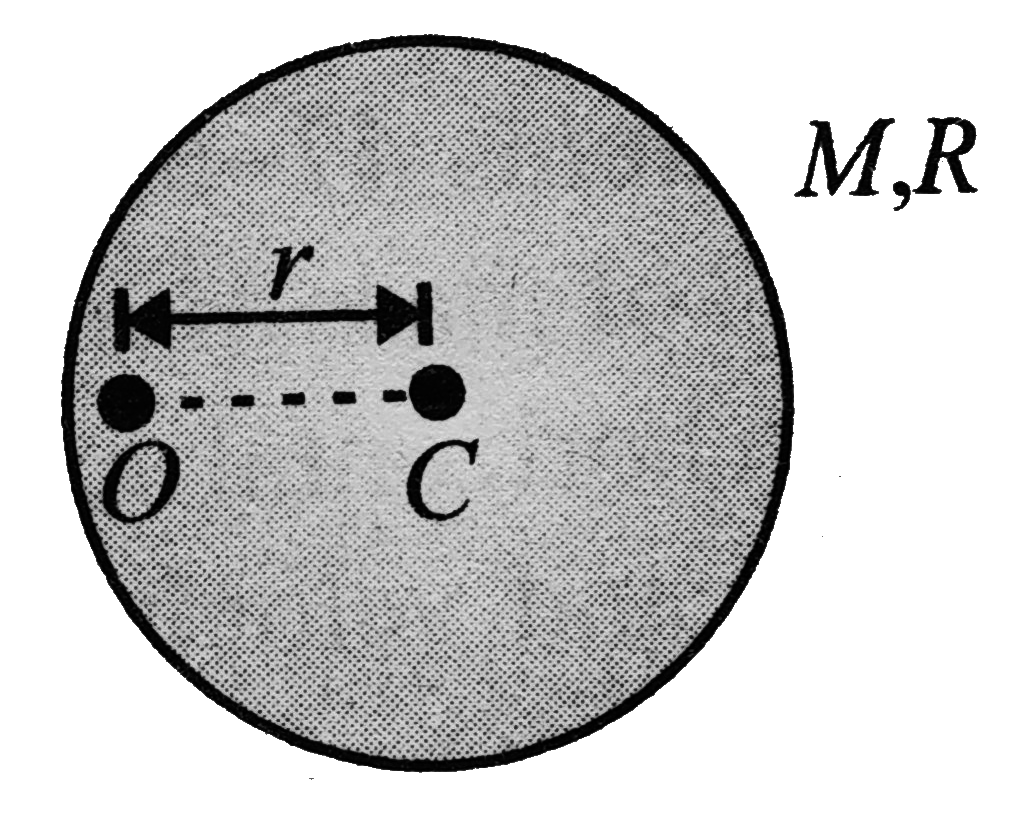
The angular velocity of the disc in the above described case is View SolutionQuestion 268
A disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at this instant isView SolutionQuestion 269
In the given figure F=10N,R=1m, mass of the body is 2kg and moment of inertia of the body about an axis passing through O and perpendicular to the plane of the body is 4kgm2. O is the centre of mass of the body.
If the ground is smooth, what is the total kinetic energy of the body after 2s?View SolutionQuestion 270
In the given figure F=10N,R=1m, mass of the body is 2kg and moment of inertia of the body about an axis passing through O and perpendicular to the plane of the body is 4kgm2. O is the centre of mass of the body.
If the ground is sufficiently rough to ensure rolling, what is the kinetic energy of the body now in the given time interval of 2s?View SolutionQuestion 279
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
The angular velocity of the disc after the particle sticks to it isView SolutionQuestion 280
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc isView SolutionQuestion 281
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
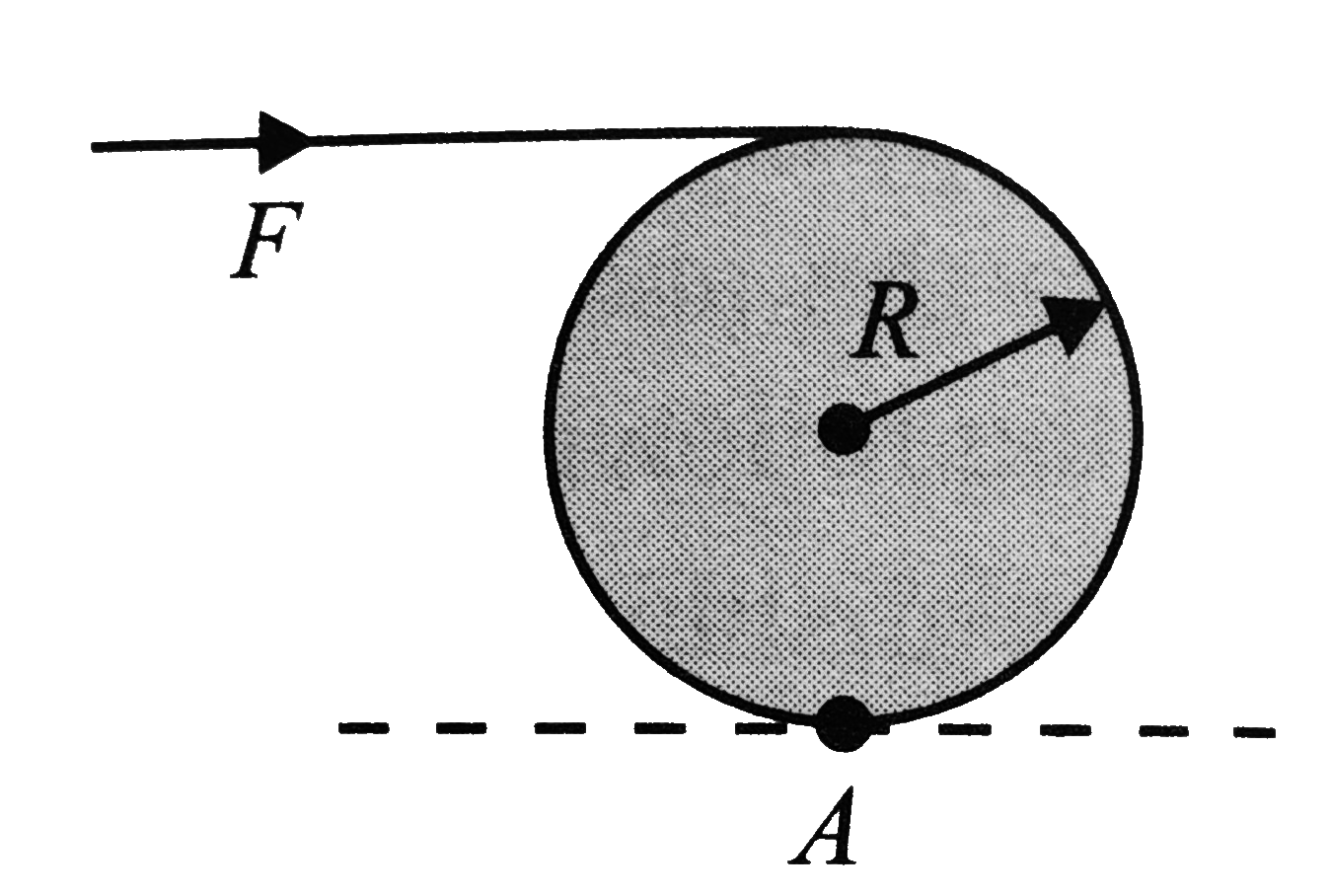
Tangential acceleration of the centre of mass isView SolutionQuestion 282
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
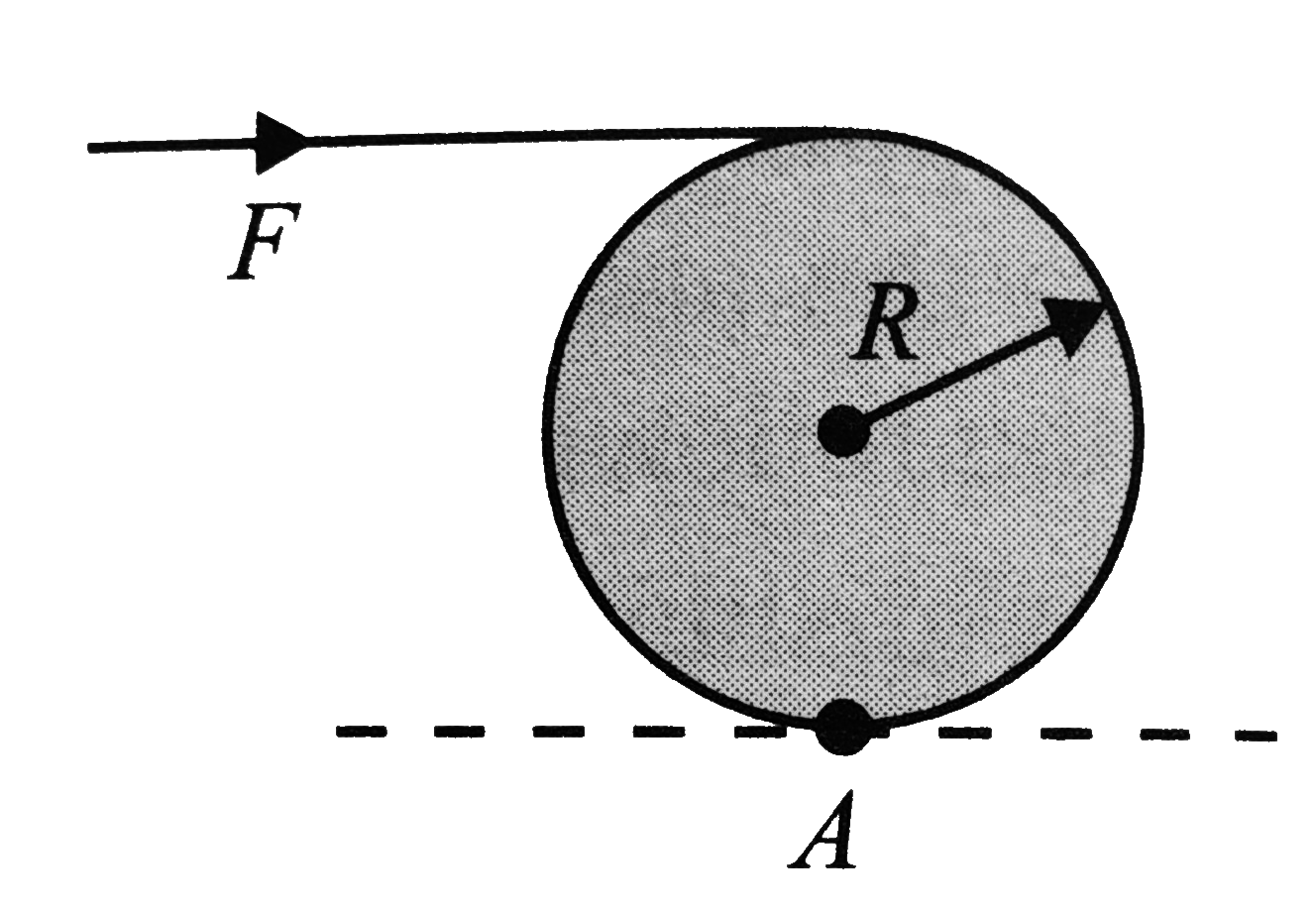
Component of reaction at the hinge in the vertical direction is View SolutionQuestion 283
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
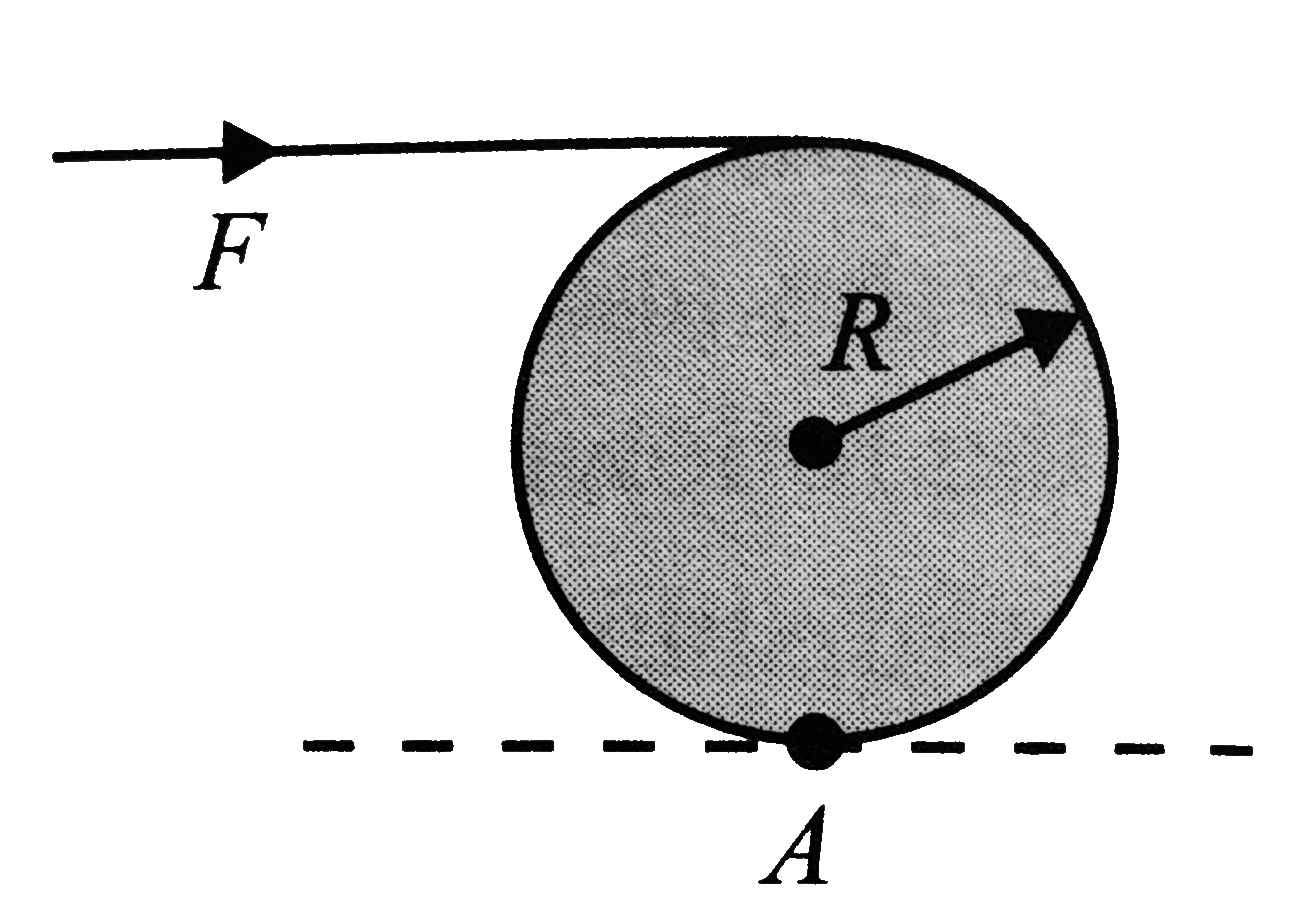
Component of reaction at the hinge in the horizontal direction is View SolutionQuestion 284
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle A of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following:
a. The ratio M/m.
b. The angular velocity of the rod about O.
c. The coefficient of restitution 'e' for the collision.
d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
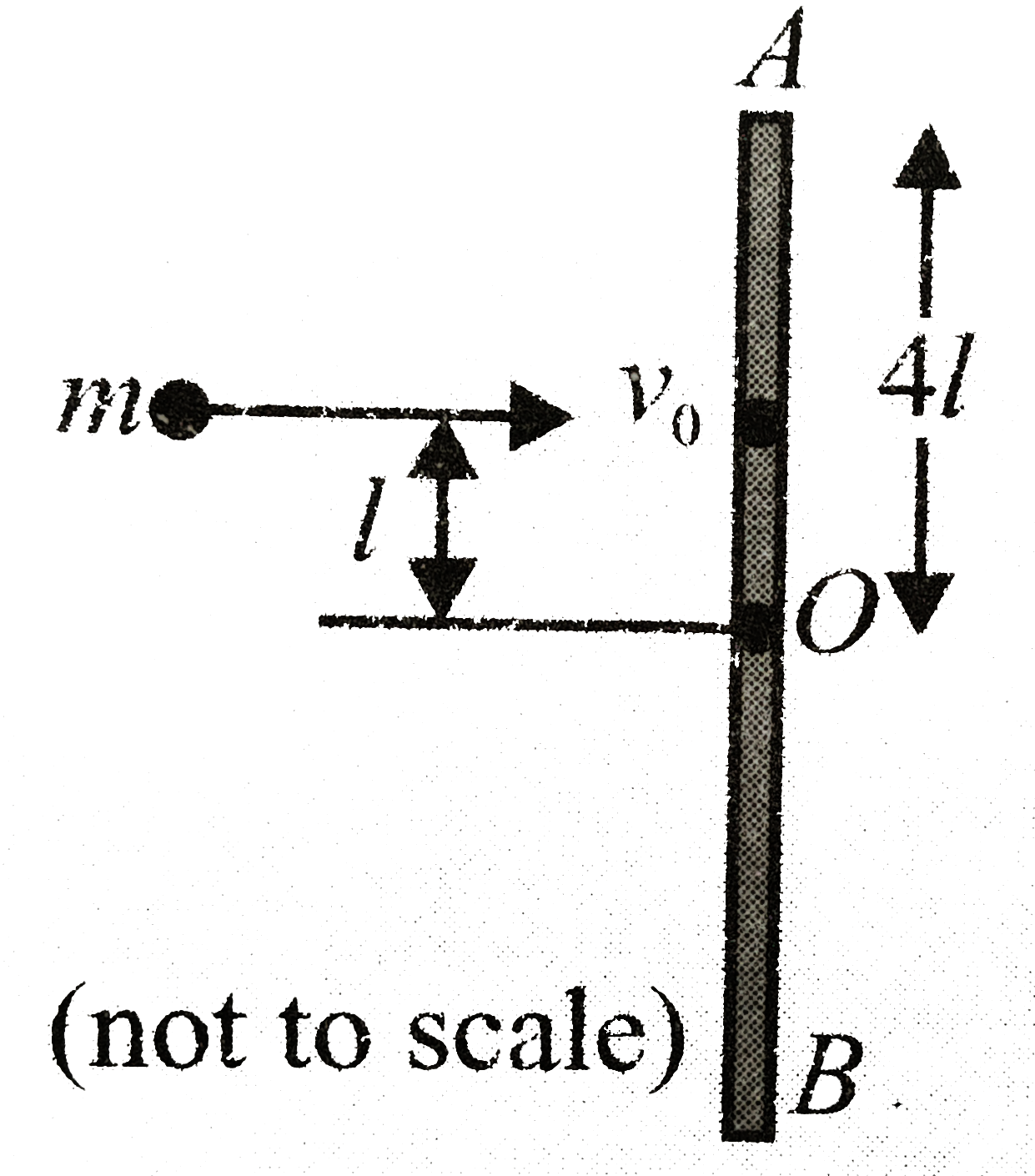 View Solution
View SolutionQuestion 285
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle A of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following:
a. The ratio M/m.
b. The angular velocity of the rod about O.
c. The coefficient of restitution 'e' for the collision.
d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
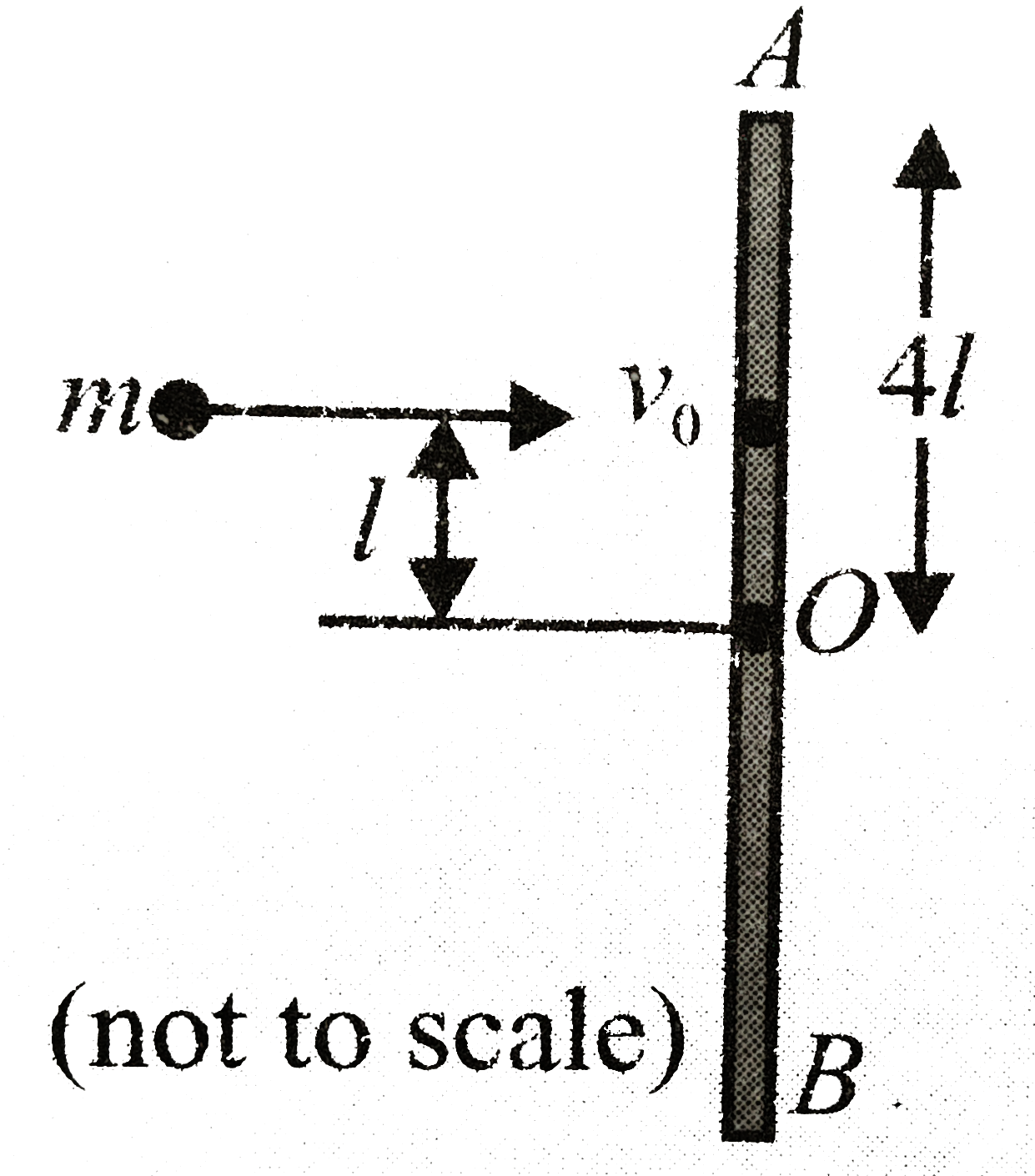 View Solution
View SolutionQuestion 286
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle A of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following:
a. The ratio M/m.
b. The angular velocity of the rod about O.
c. The coefficient of restitution 'e' for the collision.
d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
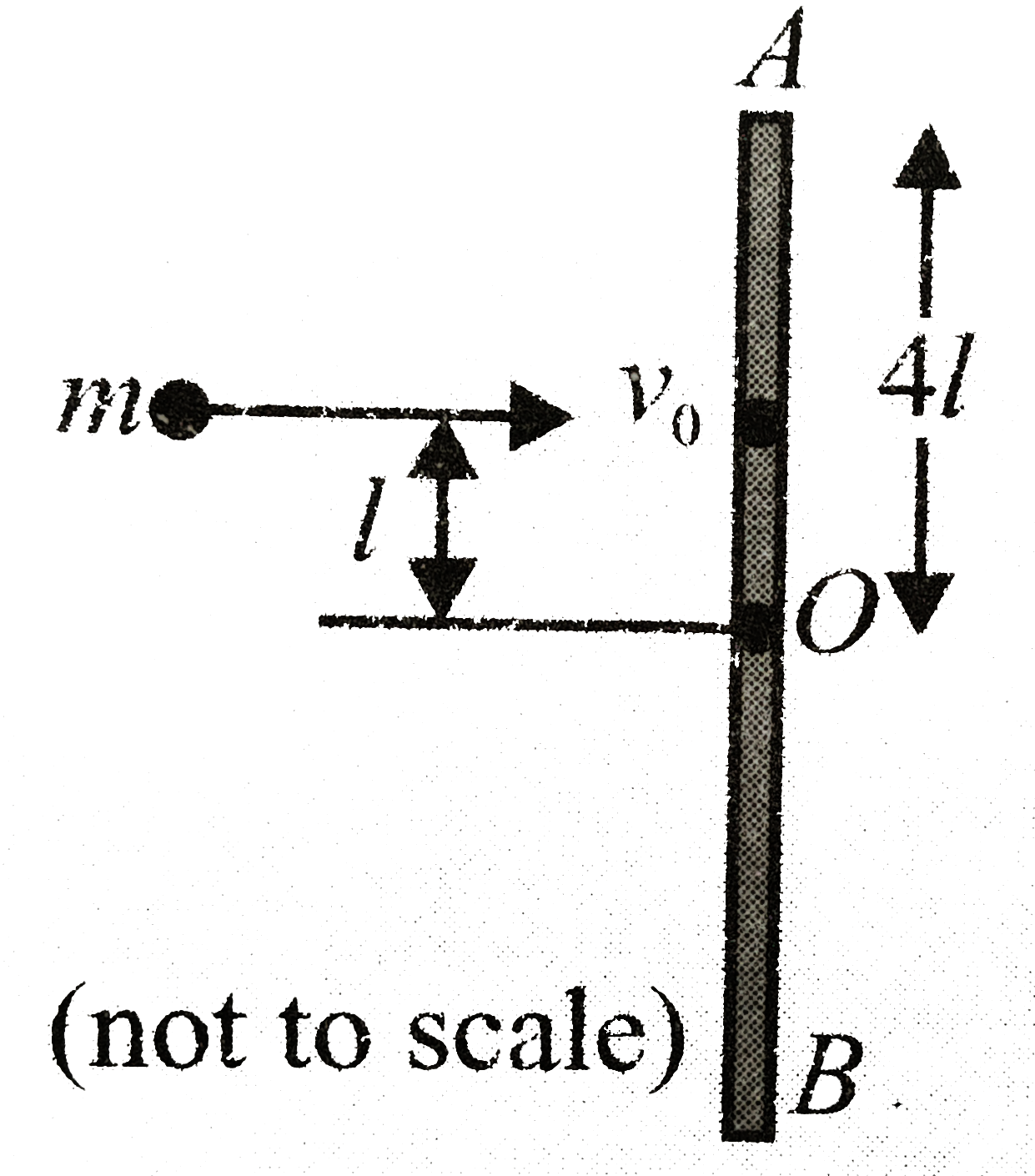 View Solution
View SolutionQuestion 287
A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle A of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following:
a. The ratio M/m.
b. The angular velocity of the rod about O.
c. The coefficient of restitution 'e' for the collision.
d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
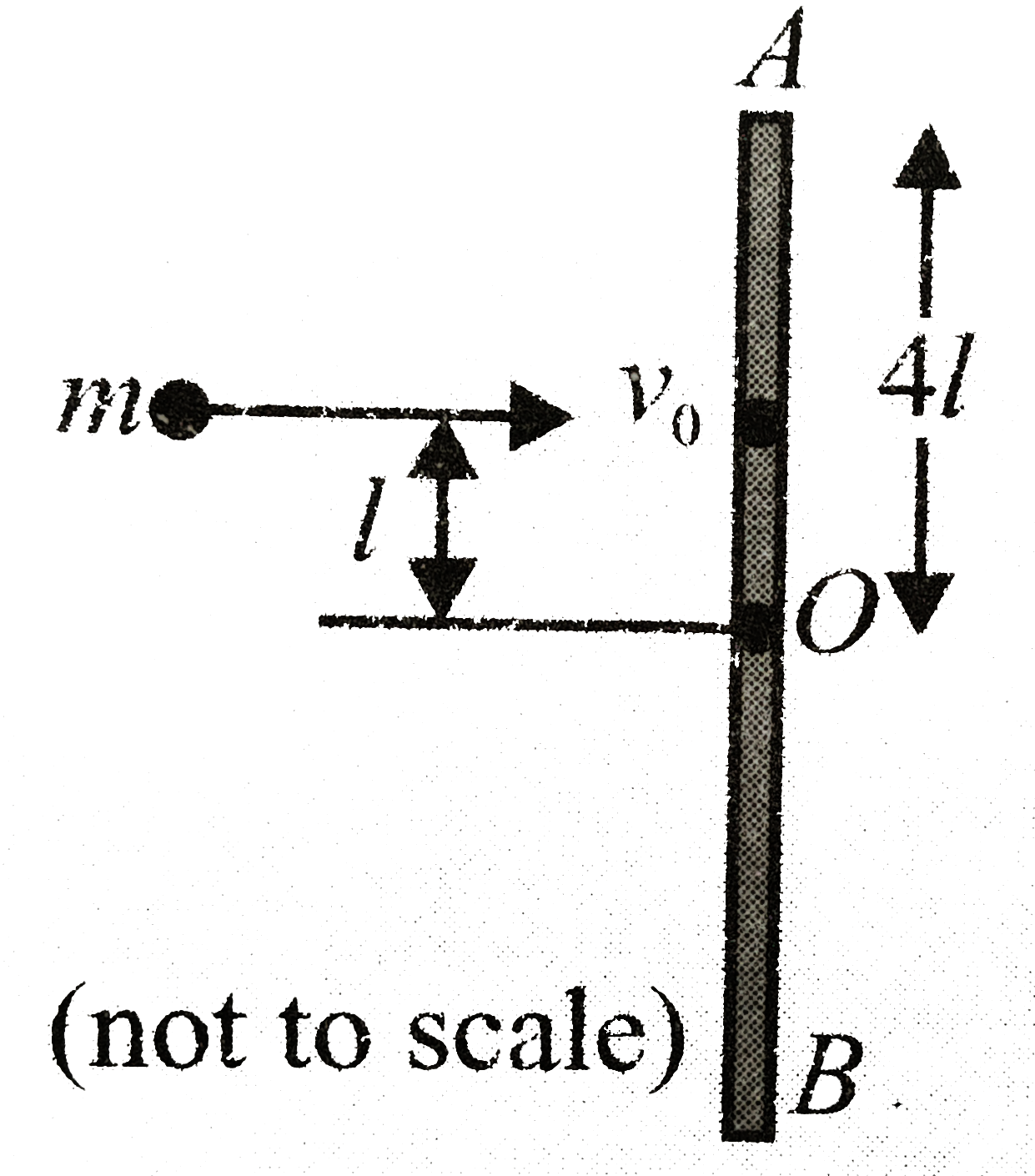 View Solution
View SolutionQuestion 290
A Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
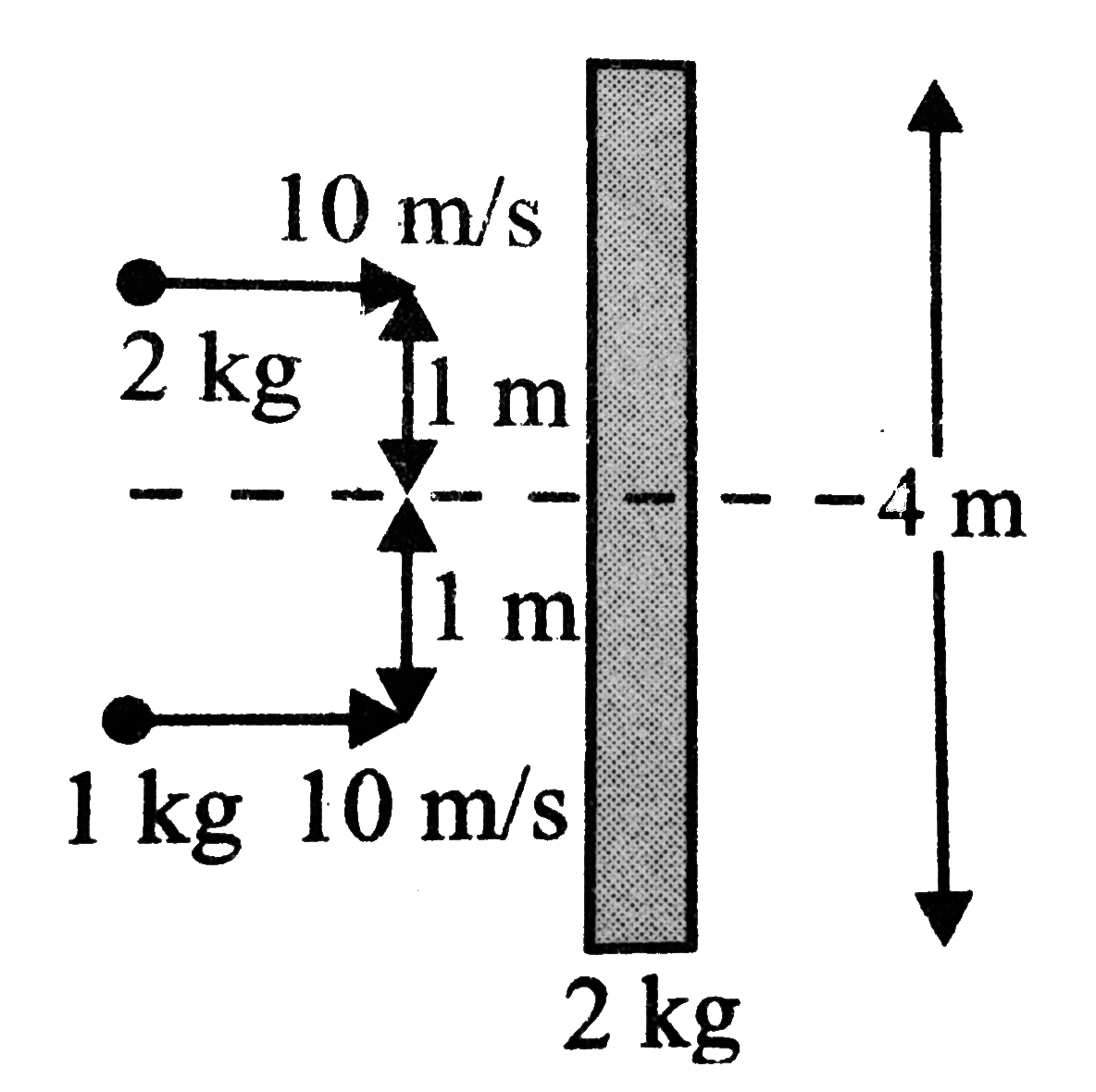
, If the two particles strike the rod in opposite direction, then after collision, as compared to the previous situation the rod will View SolutionQuestion 291
A spherical ball of mass M moving with initial velocity V collides elastically with another ball of mass M, which is fixed at one end of L shaped rigid massless frame as shown in Fig. (a). The L shaped frame contains another mass M connected at the other end.
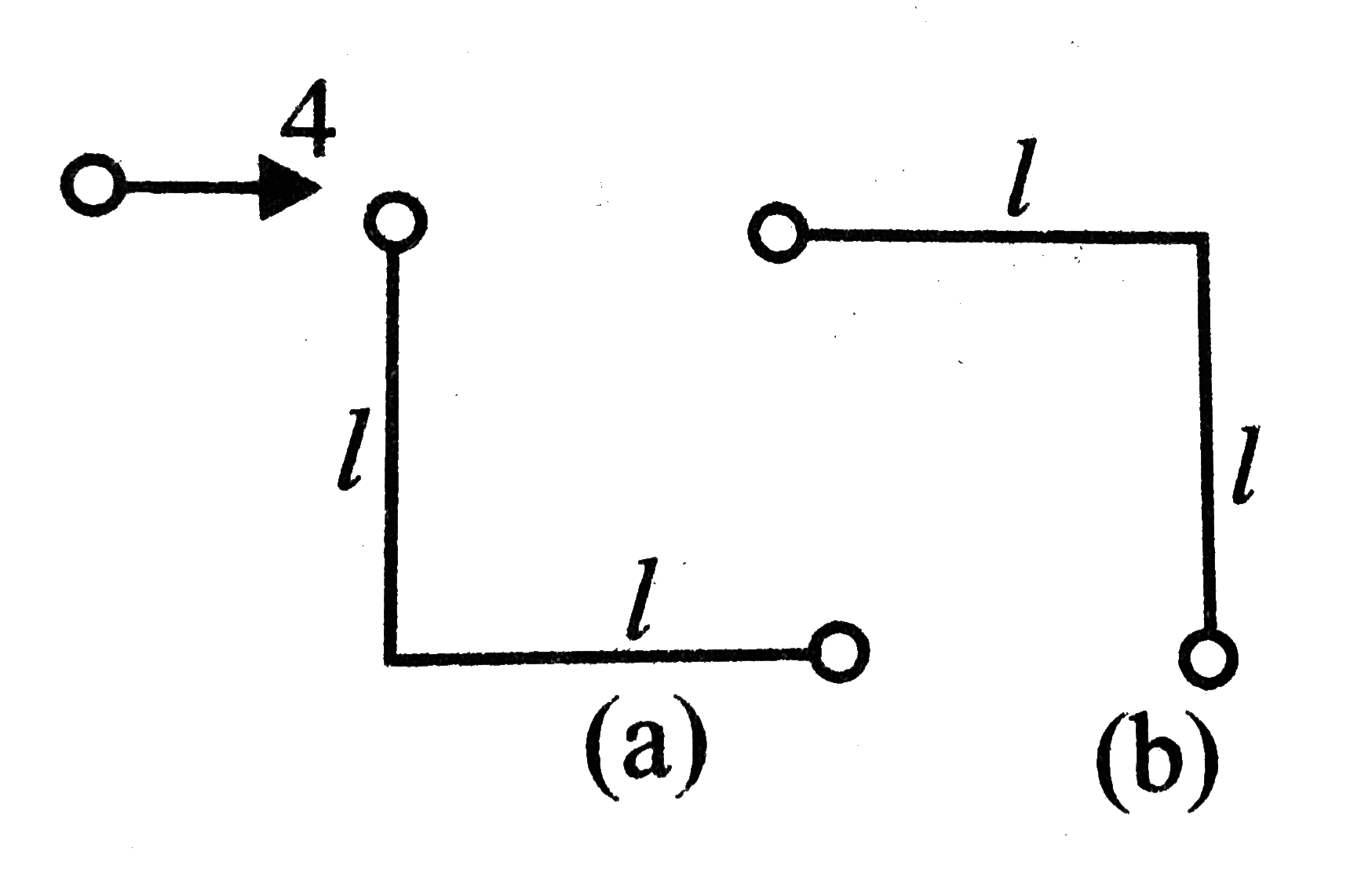
The speed of the striking mass after collision is View SolutionQuestion 292
A spherical ball of mass M moving with initial velocity V collides elastically with another ball of mass M, which is fixed at one end of L shaped rigid massless frame as shown in Fig. (a). The L shaped frame contains another mass M connected at the other end.
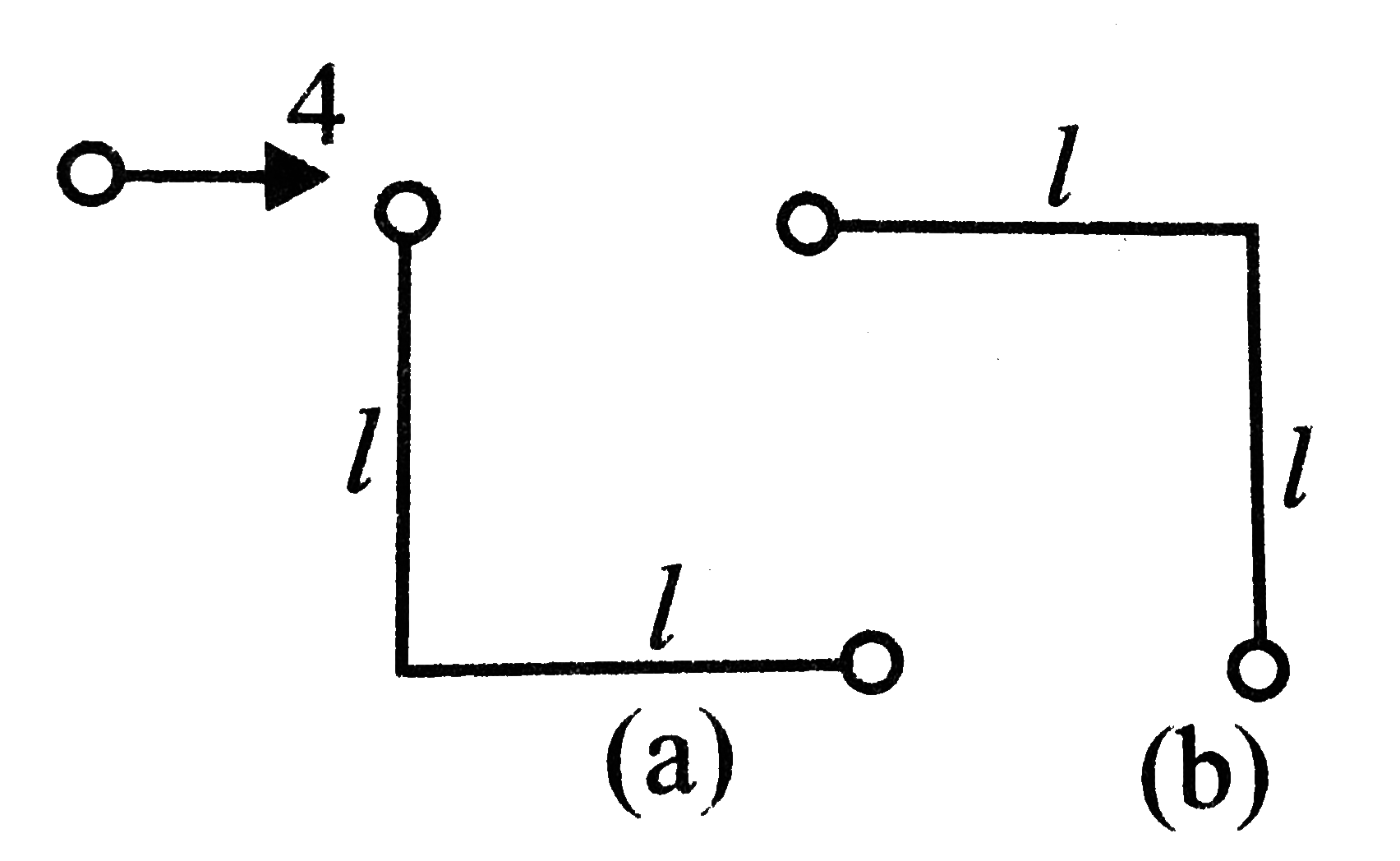
The angular speed of L frame immediately after collisionView SolutionQuestion 293
A spherical ball of mass M moving with initial velocity V collides elastically with another ball of mass M, which is fixed at one end of L shaped rigid massless frame as shown in Fig. (a). The L shaped frame contains another mass M connected at the other end.
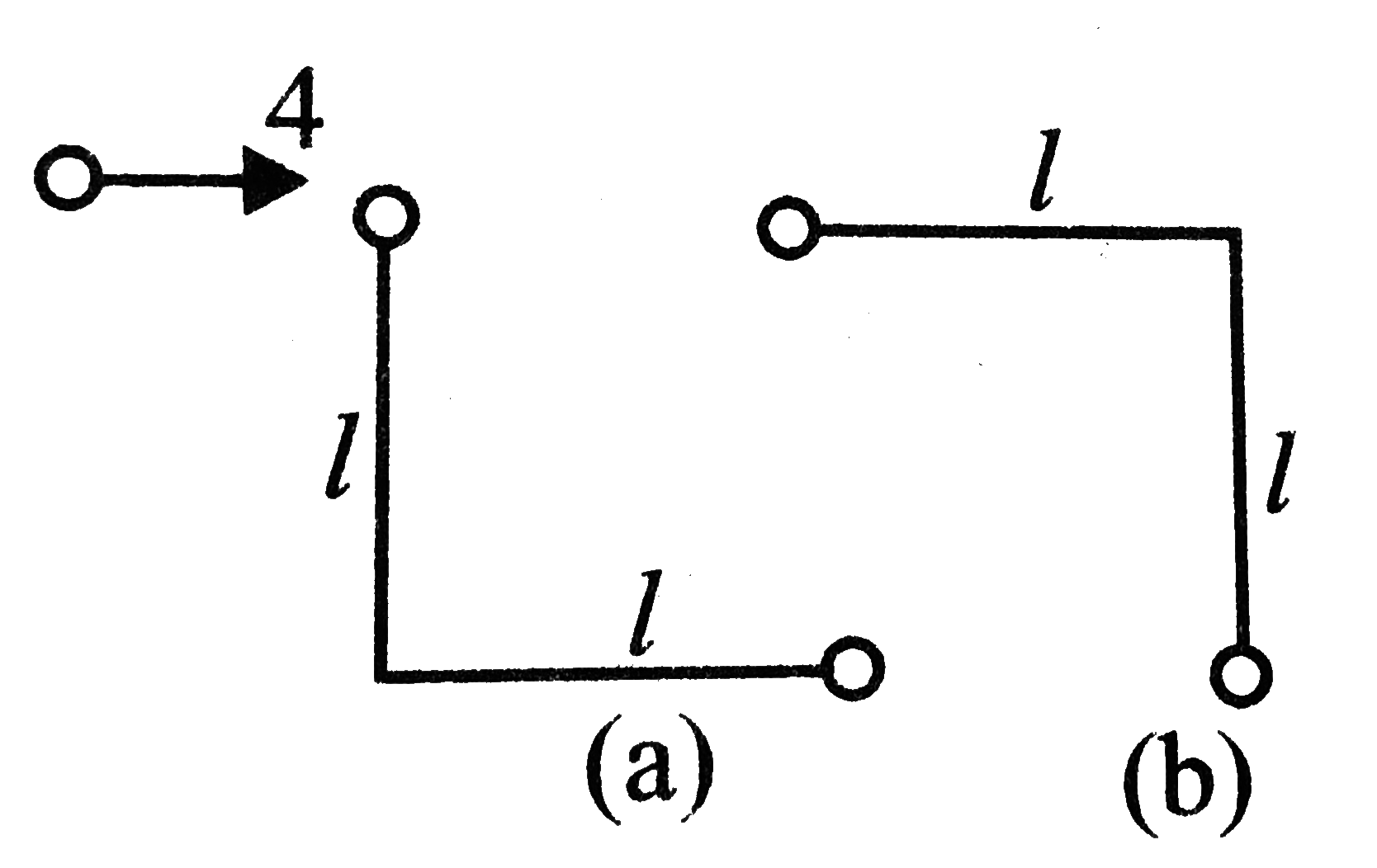
How soon will the frame come to the orientation shown in Fig. (b) after collision? View SolutionQuestion 295
A solid cylinder of mass m is kept in balance on a fixed incline of angle α=37∘ with the help of a thread fastened to its jacket. The cylinder does not slip.

In what direction should the thread be pulled to minimise the force required to hold the cylinder? What is the magnitude of this force?View SolutionQuestion 298
A ball, rolling purely on a horizontal floor with centre's speed v, hits a smooth vertical wall surface elastically. Answer the following questions.
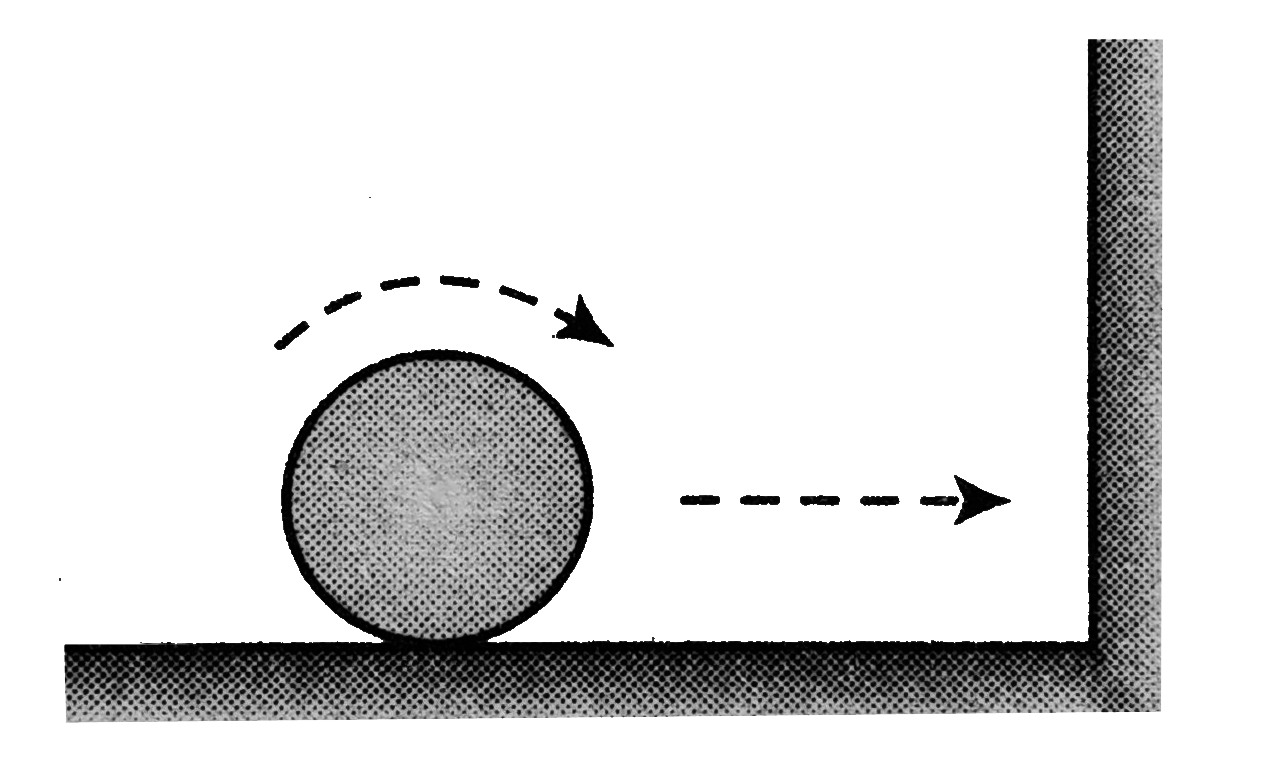
The change in angular momentum of the solid ball (mass m, radius R), about the corner point of floor and wall, due to the collision is View SolutionQuestion 299
A uniform disc of mass 1kg and radius 20cm is rolling purely on a flat horizontal surface. Its centre C is moving with acceleration a=20ms−2 and velocity v=4m/s at a certain instant. At this instant. points A and B are located on the disc as shown in the diagram, with AC=BC=10cm.

What is the kinetic energy of the disc? View SolutionQuestion 300
A uniform disc of mass 1kg and radius 20cm is rolling purely on a flat horizontal surface. Its centre C is moving with acceleration a=20ms−2 and velocity v=4m/s at a certain instant. At this instant. points A and B are located on the disc as shown in the diagram, with AC=BC=10cm.
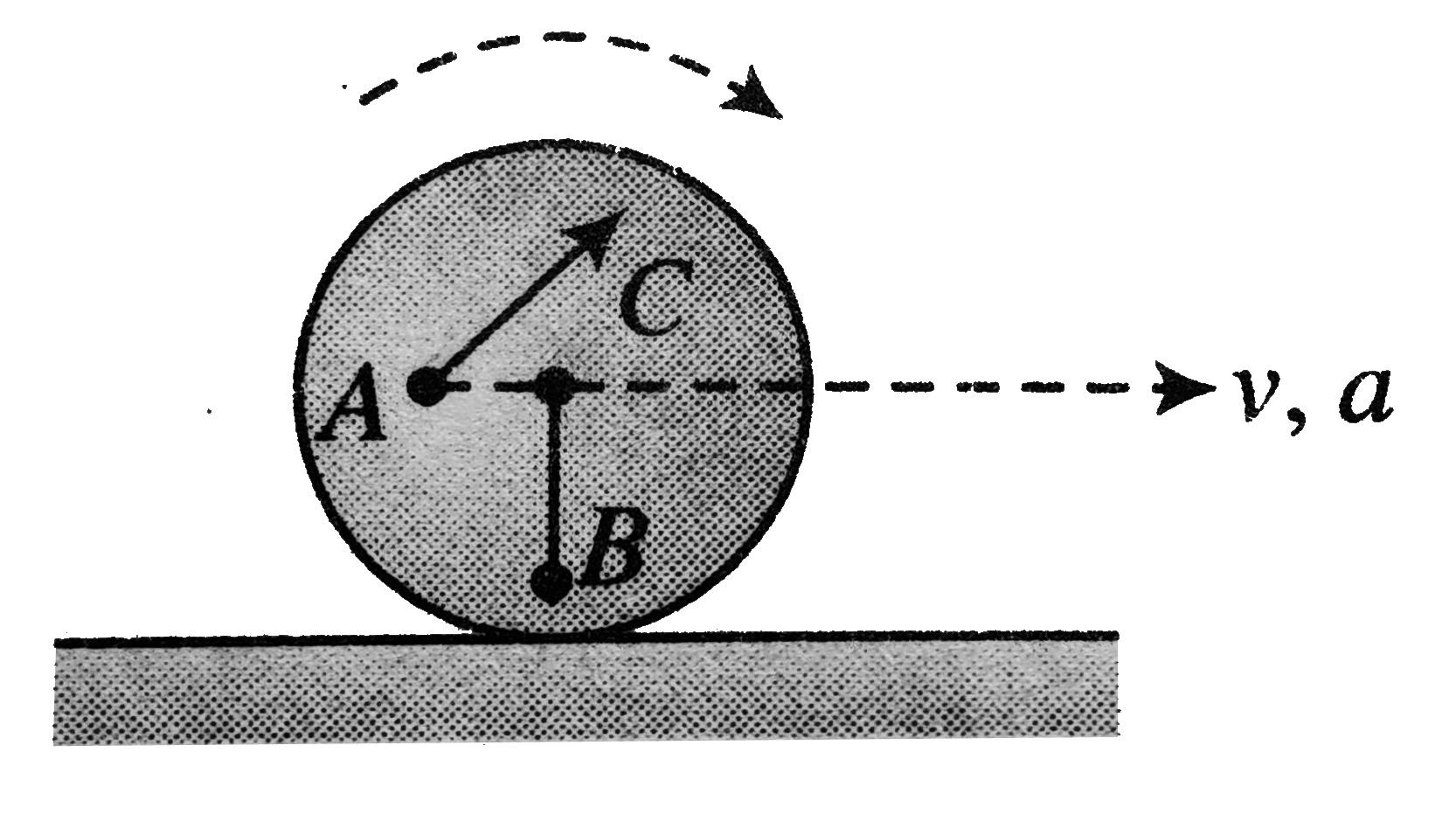
What is the acceleration magnitude of point A? View SolutionQuestion 301
A uniform disc of mass 1kg and radius 20cm is rolling purely on a flat horizontal surface. Its centre C is moving with acceleration a=20ms−2 and velocity v=4m/s at a certain instant. At this instant. points A and B are located on the disc as shown in the diagram, with AC=BC=10cm.

What is the acceleration magnitude of point B? View SolutionQuestion 302
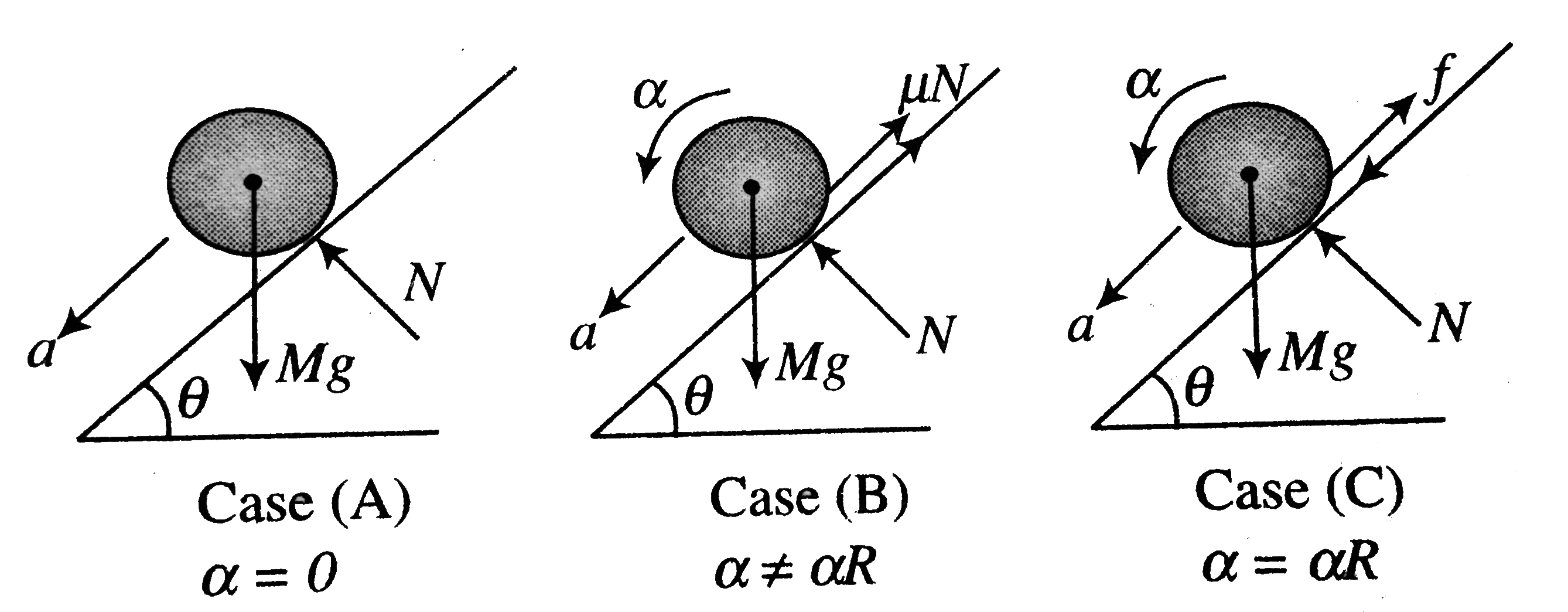
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
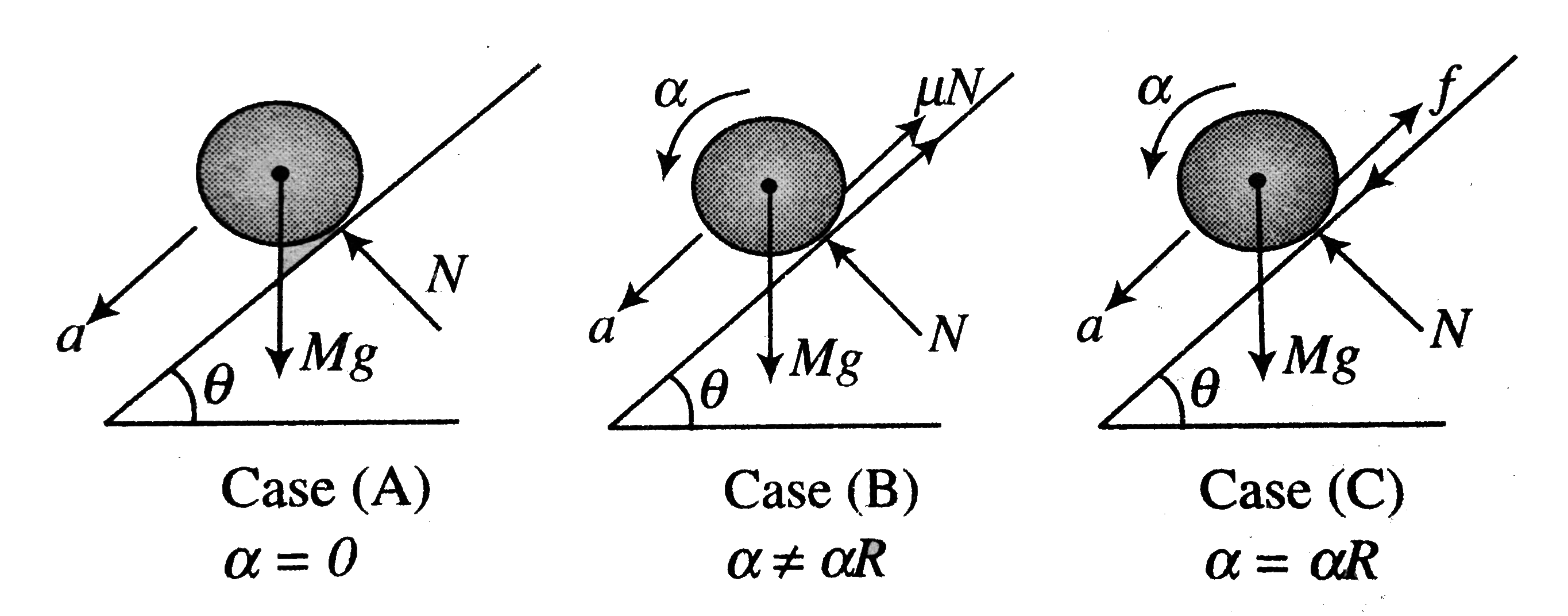
Three solid uniform spheres are released on an inclined plane as shown in the figure. The distance between the spheres remains constant during motion in:
 View Solution
View SolutionQuestion 303
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
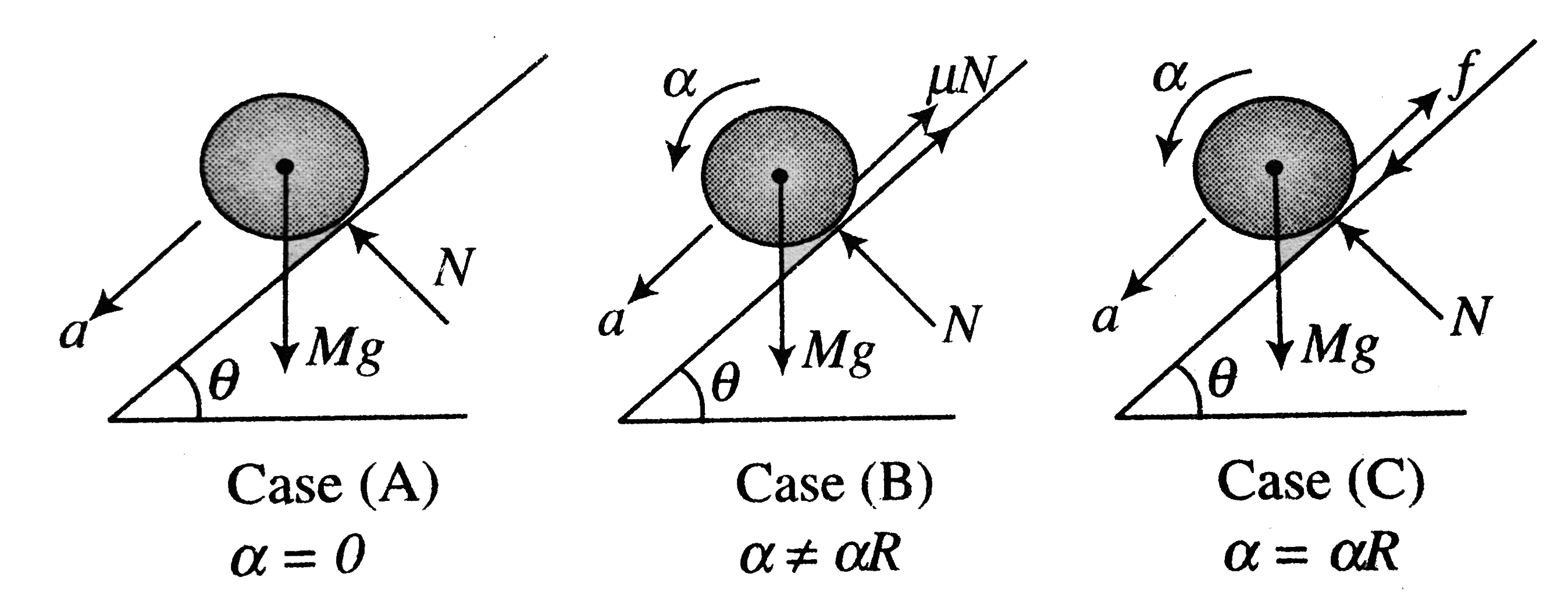
We have four objects: a solid sphere, a hollow sphere, a ring and a disc, all of same radius. When these are released on an inclined plane, it may happen that all of them do not perform pure rolling. But from the information of pure rolling, if one object can be confirmed to be purely rolling then it can be said that rest all will perform pure rolling. This object whose pure rolling confirms pure rolling of all other objects isView SolutionQuestion 304
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
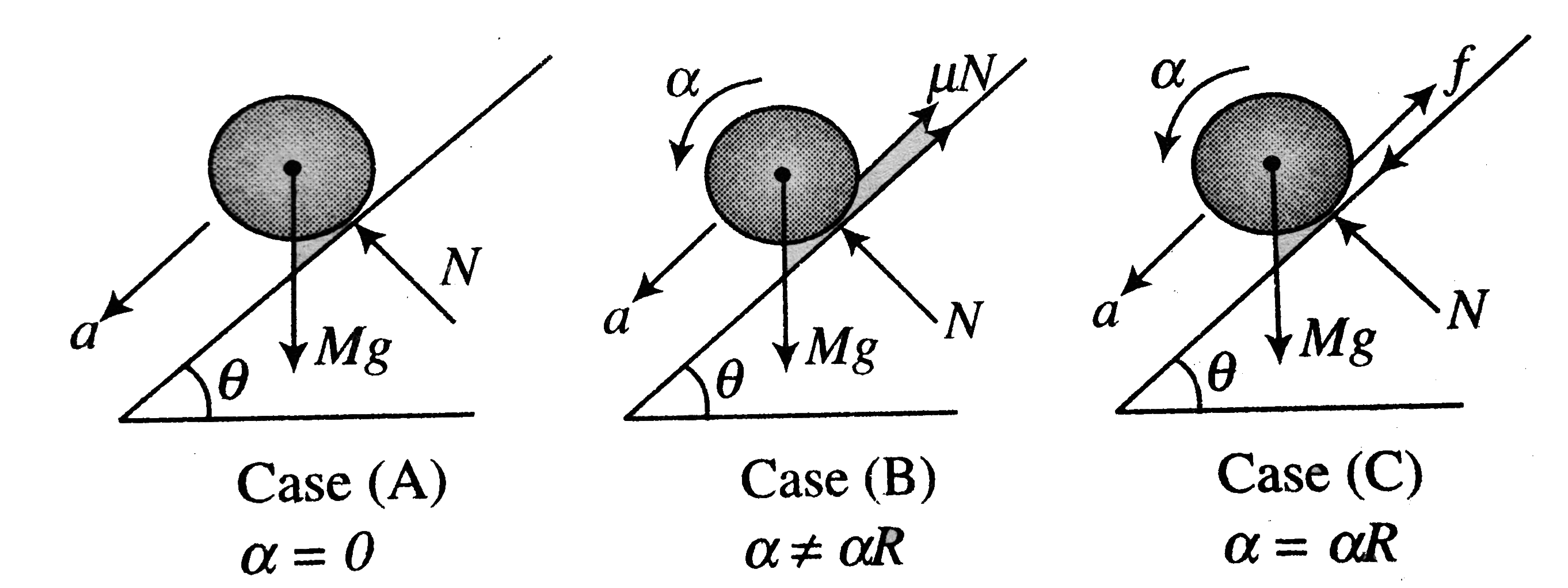
If the four objects given in the above question are of same mass, same radius having the same friction coefficient and are released from the same height, then at the bottom the object which will have least kinetic energy for case B will be the:View SolutionQuestion 305
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
Two children A and B use bicycles, having wheels of ring type and disc type respectively. During a race, bicycles are given the same velocity from the bottom of the inclined bridge to ascend the bridge without pedalling, then (assuming pure rolling). View SolutionQuestion 310
A solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity (in m/s) of the sphere in horizontal direction immediately after the impact (given: Rω=5).
 View Solution
View SolutionQuestion 311
A wheel A is connected to a second wheel B by means of inextensible string, passing over a pulley C, which rotates about a fixed horizontal axle O, as shown in the figure. The system is released from rest. The wheel A rolls down the inclined plane OK thus pulling up wheel B which rolls along the inclined plane ON.
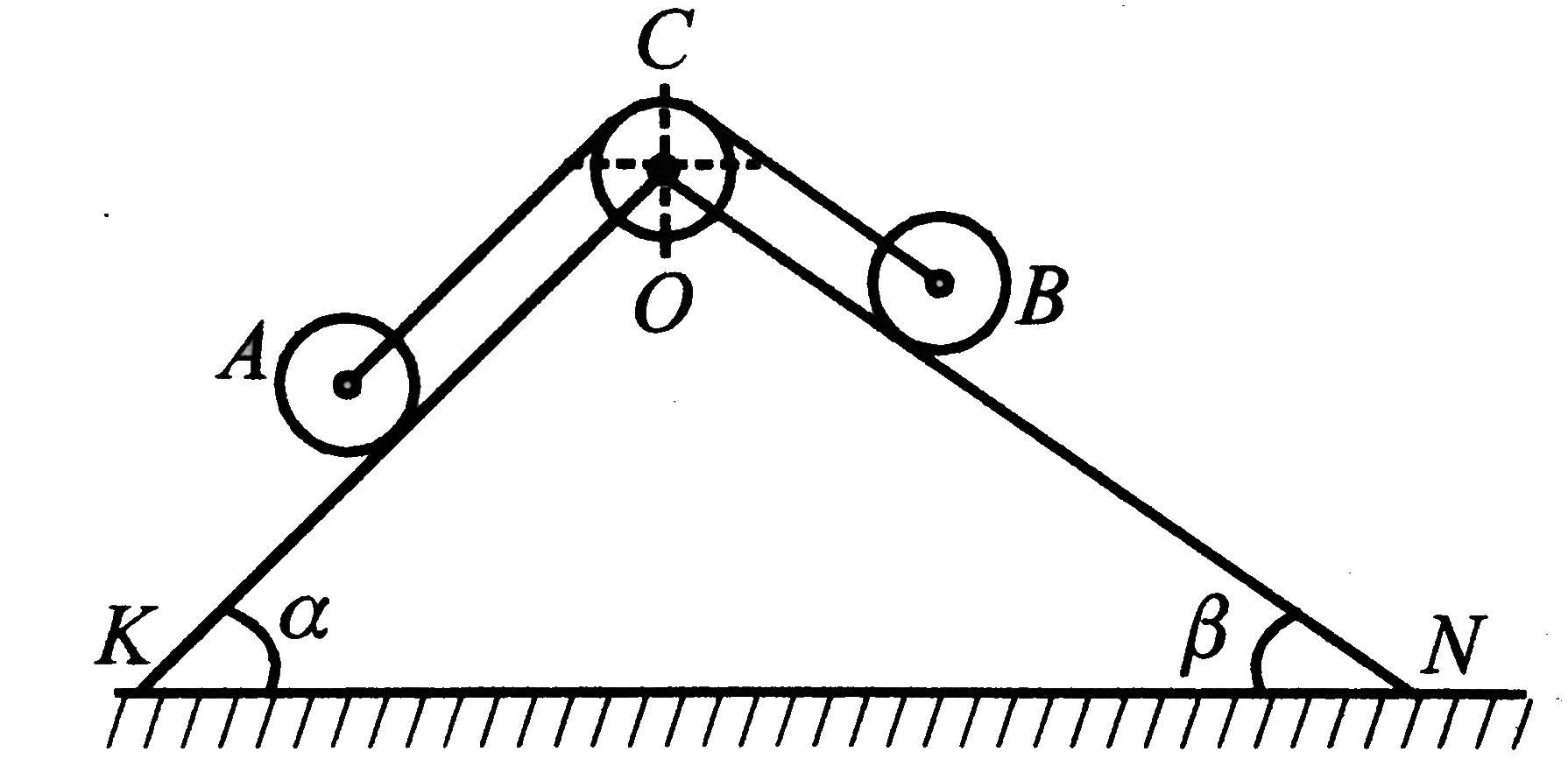
Determine the velocity (in m/s) of the axle of wheel A, when it has travelled a distance s=3.5m down the to be slope. Both wheels and the pulley are assumed homogeneous disks of identical weight and radius. Neglect the weight of the string. The string does not over C. [Take α=53∘ and β=37∘]View SolutionQuestion 314
A boy is pushng a ring of mass 2kg and radius 0.5 m with a stick as shwon in figure. The stick applies a force of 2N on the ring and rolls it without slipping with an accelertaion of 0.3ms2. The coefficinet of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring of (P/10). The value of P is
 View Solution
View SolutionQuestion 324
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?View SolutionQuestion 325
A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 View Solution
View SolutionQuestion 326
A cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................View SolutionQuestion 327
A stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by T=Arn where A is a constant, r is the instantaneous radius of the circle and n=....View SolutionQuestion 328
A uniform disc of mass m and radius R is rolling up a rough inclined plane which makes an angle of 30∘ with the horizontal. If the coefficients of static and kinetic friction are each equal to μ and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane. View SolutionQuestion 330
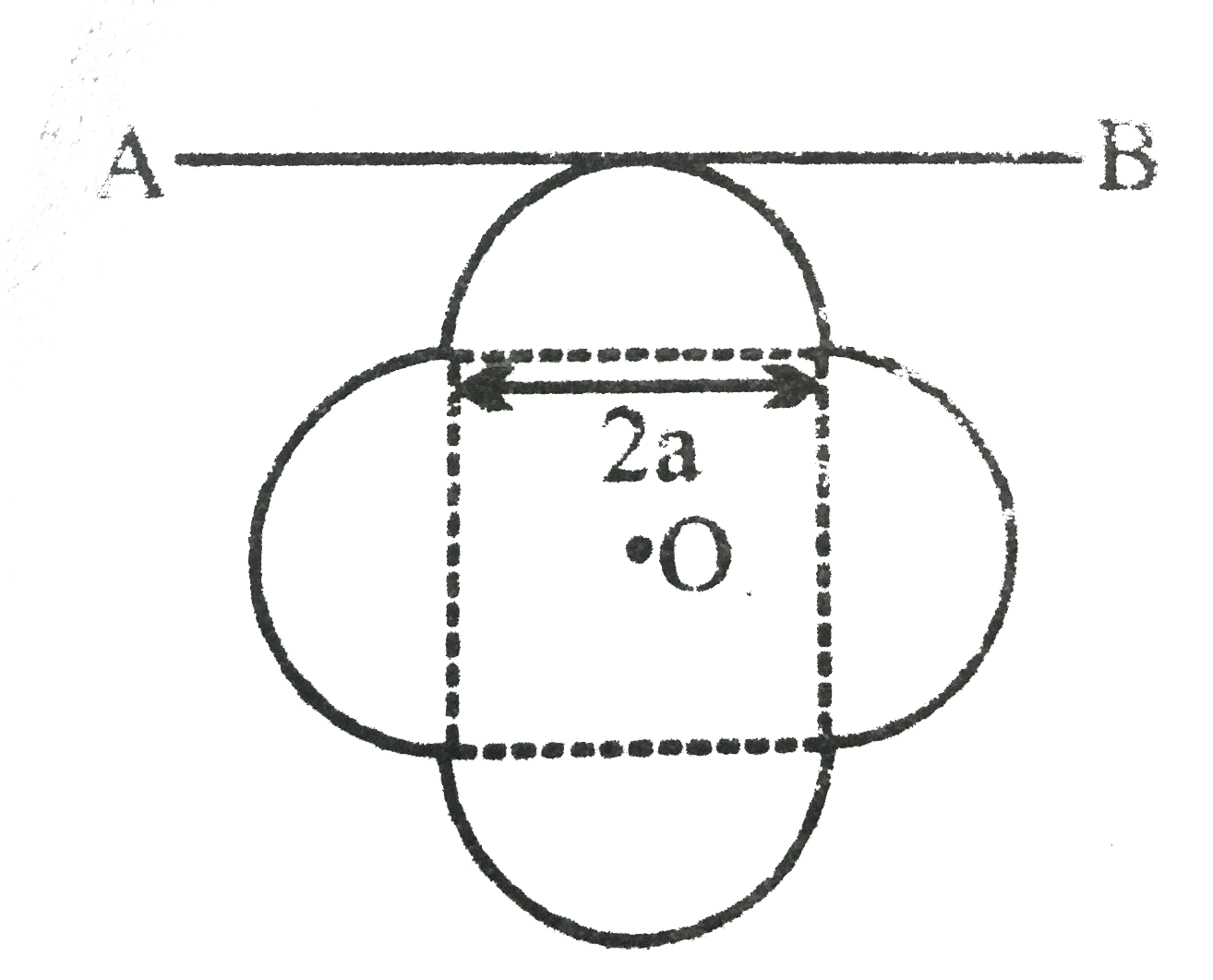
A symmetric lamina of mass M consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of lamina is.
 .View Solution
.View SolutionQuestion 331
A triangular plate of uniform thickness and density is made to rotate about an axis perpendicular to the plane of the paper and (a) passing through A,(b) passing through B, by the application of the same force, F, at C (midpoint of AB) as shown in the figure. The angular acceleration in both the cases will be the same.
 View Solution
View SolutionQuestion 332
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. another disc of the same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is 2ω/√5.View SolutionQuestion 333
A ring of mass 0.3 kg and radius 0.1 m and a solid cylinder of mass 0.4 kg and of the same radius are given the same kinetic energy and released simultaneously on a flat horizontal surface towards a wall which is at the same distance from the ring and the cylinder. The rolling friction in both cases is negligible. The cylinder will reach the wall first.View SolutionQuestion 334
Two particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.View SolutionQuestion 336
Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of View SolutionQuestion 338
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and centre of mass velocity υ. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωAandωB respectively. ThenView SolutionQuestion 341
A long horizontal rod has a bead which can slide along its length and initially placed at a
distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is View SolutionQuestion 342
A cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 View Solution
View SolutionQuestion 343
A thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is A cubical block of side L rests on a rough horizontal surface with coefficient of friction sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
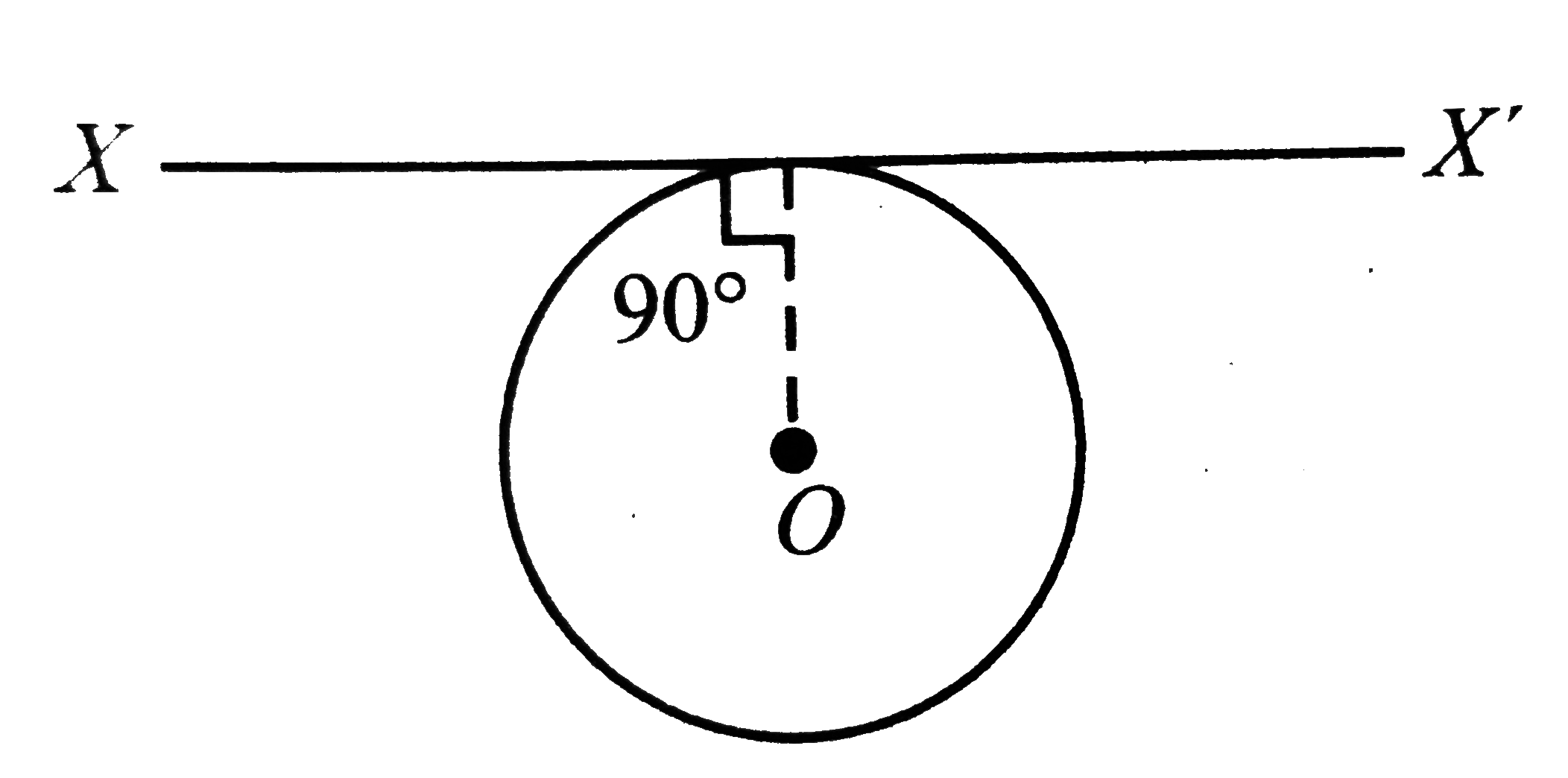 View Solution
View SolutionQuestion 344
A equilaterial triangle ABC formed from a uniform wire has two small identical beads initially located at A. The triangle is set rotating about the vertical axis AO. Then the beads are released from rest simultaneously and allowed to slide down. one long. AB and the other along AC as shown. Neglecting frictional effects, the quantities that are conserved as the beads slide down, are.
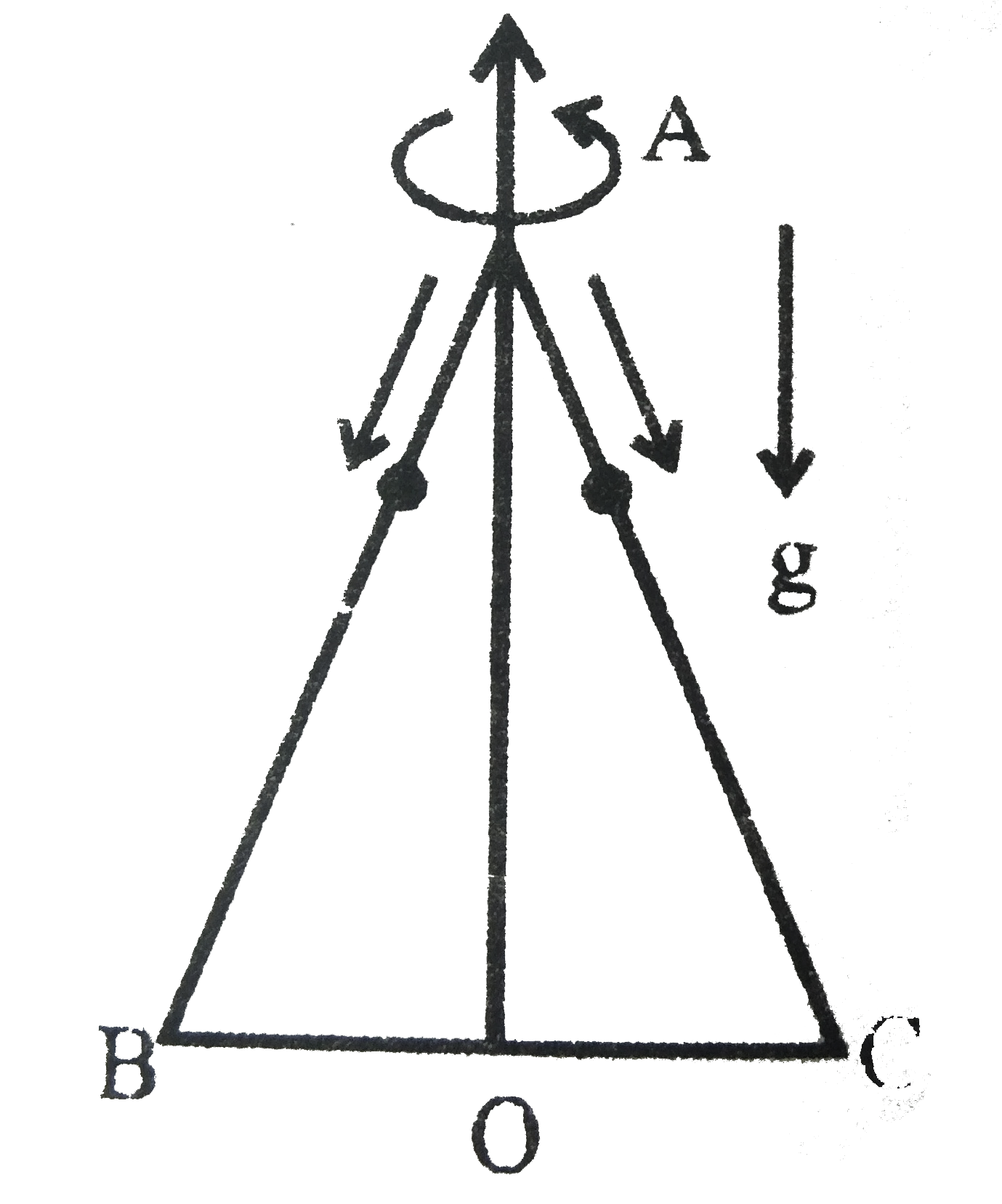 .View Solution
.View SolutionQuestion 347
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),View SolutionQuestion 350
A horizonral circular plate is rotating about a vertical axis passing through its centre with an angular velocity ω0. A man sitting at the centre having two blocks in his hands stretches out his hands so that the moment of inertia of the system doubles. If the kinetic energy of the system is K intially, its final kinetic energy will beView SolutionQuestion 355
A solid sphere of mass M, radius R and having moment of inertia about as axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains I. Then, radius of the disc will be.View SolutionQuestion 359
A thin ring of mass 2kg and radius 0.5 m is rolling without on a horizontal plane with velocity 1m/s. A small ball of mass 0.1kg, moving with velocity 20 m/s in the opposite direction hits the ring at a height of 0.75m and goes vertically up with velocity 10m/s. Immediately after the collision
 View Solution
View SolutionQuestion 360
A thin uniform rod, pivoted at O, is rotating in the horizontal plane with constatn angular speed ω, as shown in the figure. At time t = 0, a small insect starts from O and moves with constant sped v, with respect to the rod towards the other end. It reaches the end of the rod at t =T and stops. The angular speed of the system remains ω throughout. The magnitude of the torque (|→π|) about O, as a function of time is best represented by which plot?
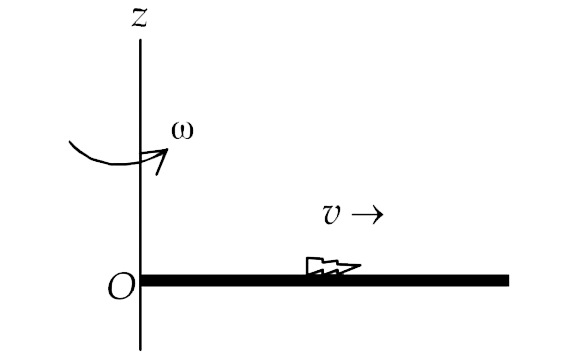 View Solution
View SolutionQuestion 361
A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed ω. If the angular momentum of the system. calculated about O and P are denoted. by →LOand→LP respectively, then.
 View Solution
View SolutionQuestion 362
Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
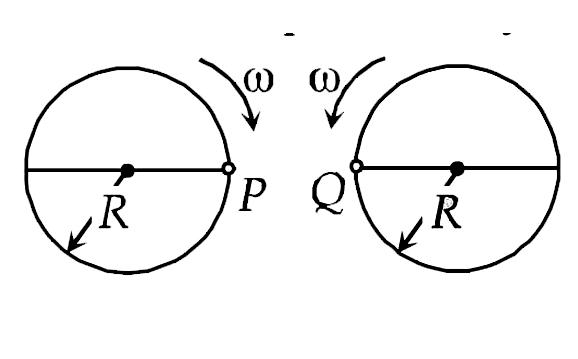 View Solution
View SolutionQuestion 363
Two solid cylinders P and Q of same mass and same radius start rolling down a fixed inclined plane from the same height at the same time. Cylinder P has most of its mass concentrated near its surface, while Q has most its mass concentrated near the axis. Which statement(s) is (are) correct?View SolutionQuestion 368
The moment of inertia of a thin square plate ABCD, fig, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
where l1,l2,l3andl4 are respectively the moments of intertial about axis 1,2,3 and 4 which are in the plane of the plate.
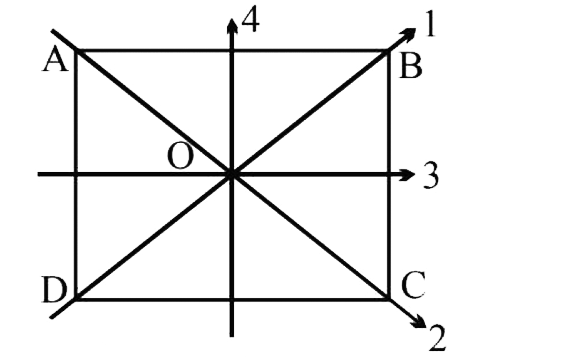 View Solution
View SolutionQuestion 371
Ler l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to View SolutionQuestion 374

A ball moves over a fixed track as shown in thre figure. From A to B the ball rolls without slipping. If surface BC is frictionless and KA,KB and KC are kinetic energies of the ball at A, B and C respectively then
(a). hA>hC,KB>KC
(b). hA>hC,KC>KA
(c). hA=hC,KB=KC
(d). hA<hC,KB>KC View SolutionQuestion 377
The figure shows a system consisting of (i) a ring the outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed ω and (ii) an inner disc of radius 2R rotating anti clockwise with angular speed ω/2. The ring and disc are separted. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of 30∘ with the horizontal. Then with respect to the horizontal surface,View SolutionQuestion 379
Two cylinders, one hollow (metal) and the other solid (wood) with the same mass identical dimensions are simulataneously allowed to roll without slipping down an inclined plane from the same height. The hollow cylinder will reach the bottom of the inclined plane first.
by the principle of conservation of energy, the total kinetic energies of both the cylinders are identical when they reach the bottom of the incline.View SolutionQuestion 380
Two discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The rotation x1/(x2 is.View SolutionQuestion 381
Two discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is View SolutionQuestion 382
Two discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -View SolutionQuestion 383
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.View SolutionQuestion 384
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
The centre of mass of the disk undergoes simple harmonic motion with angular frequency ω equal to -View SolutionQuestion 385
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.

The maximum value of V0 for whic the disk will roll without slipping is-View SolutionQuestion 386
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?View SolutionQuestion 387
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case

Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
 .
.
Which of the following statements about the instantaneous axis (passing through the centre of mass) is correct?View SolutionQuestion 388
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO ot the nearest integer is
 View Solution
View SolutionQuestion 389
A uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system isView Solution

 .
. .
.
 .
. .
.

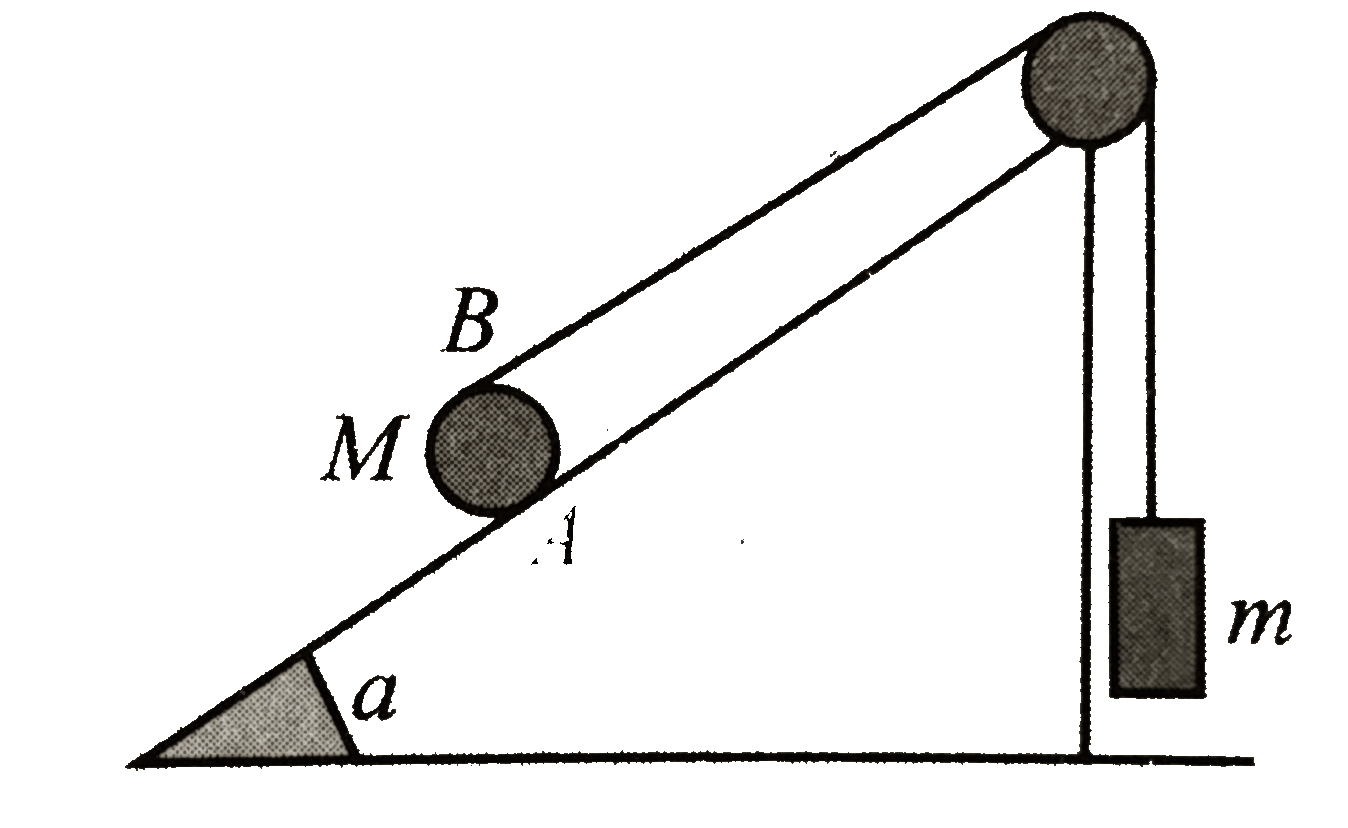


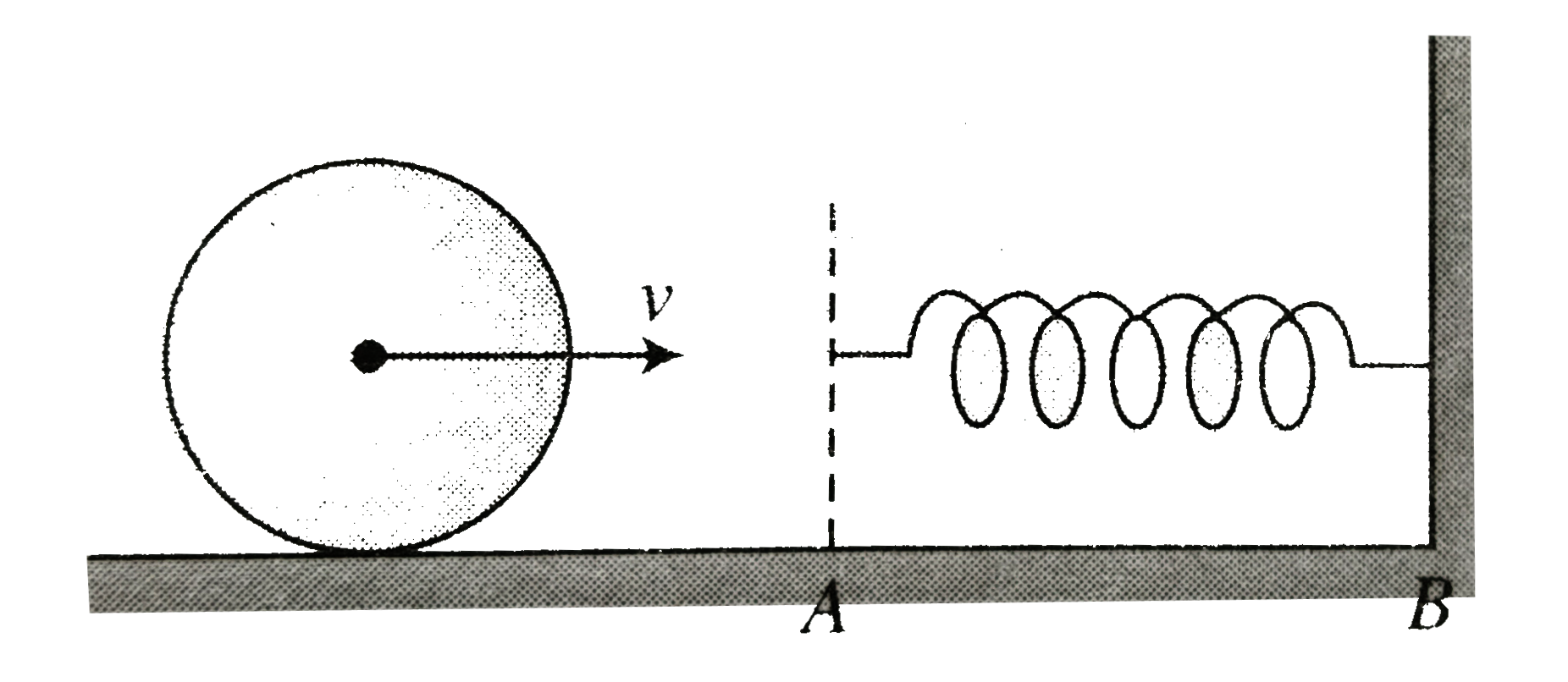

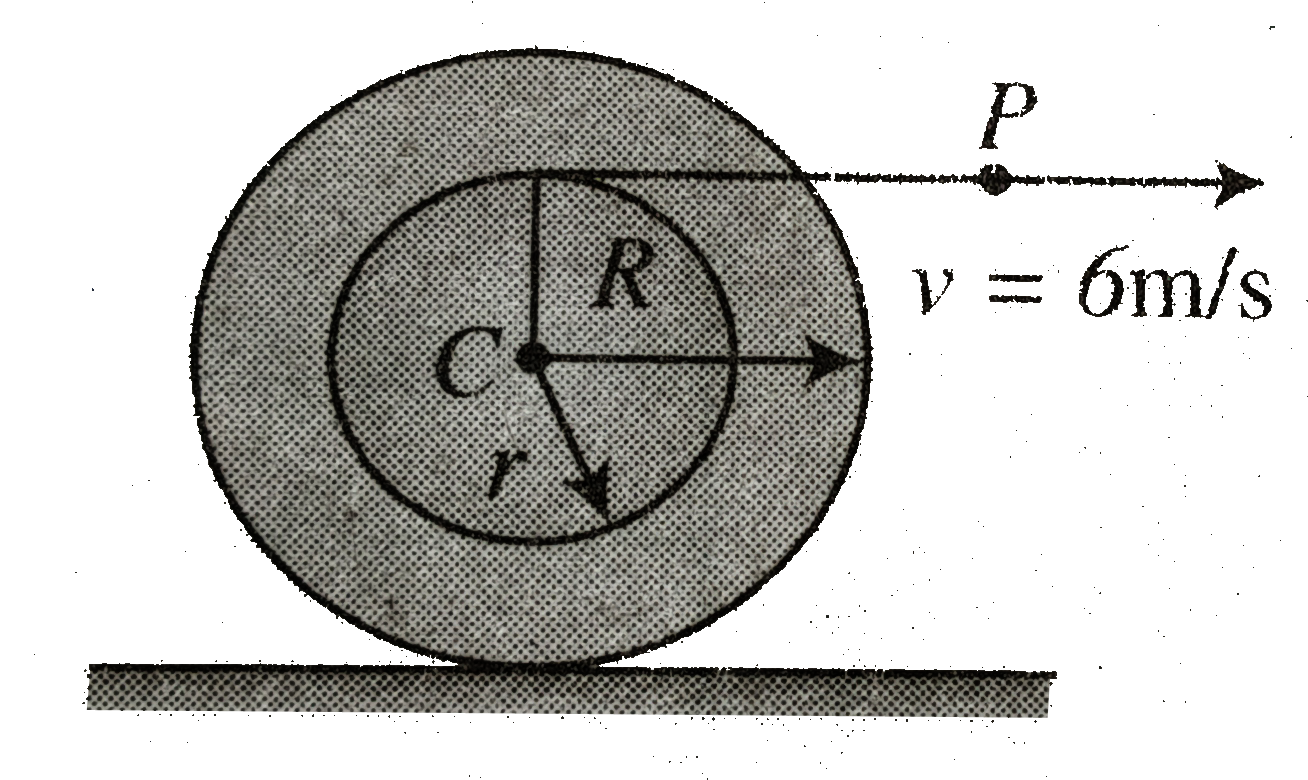
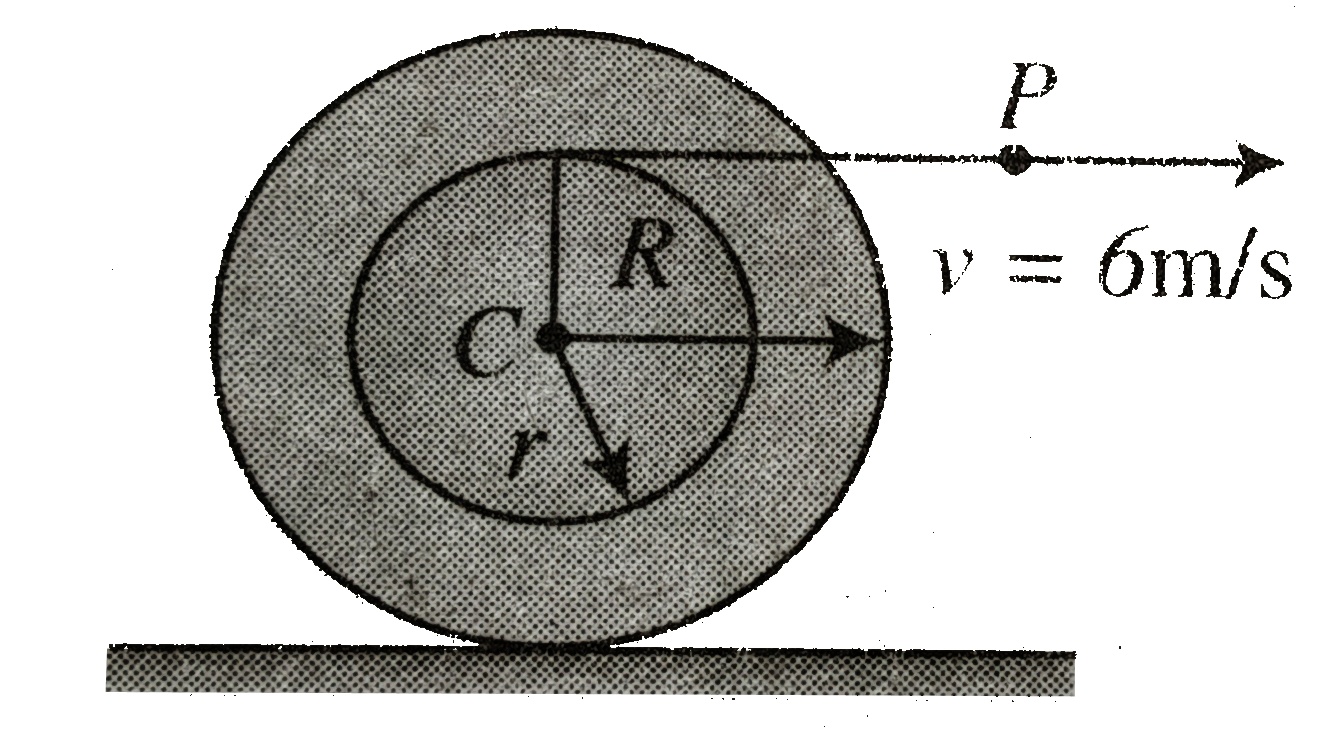

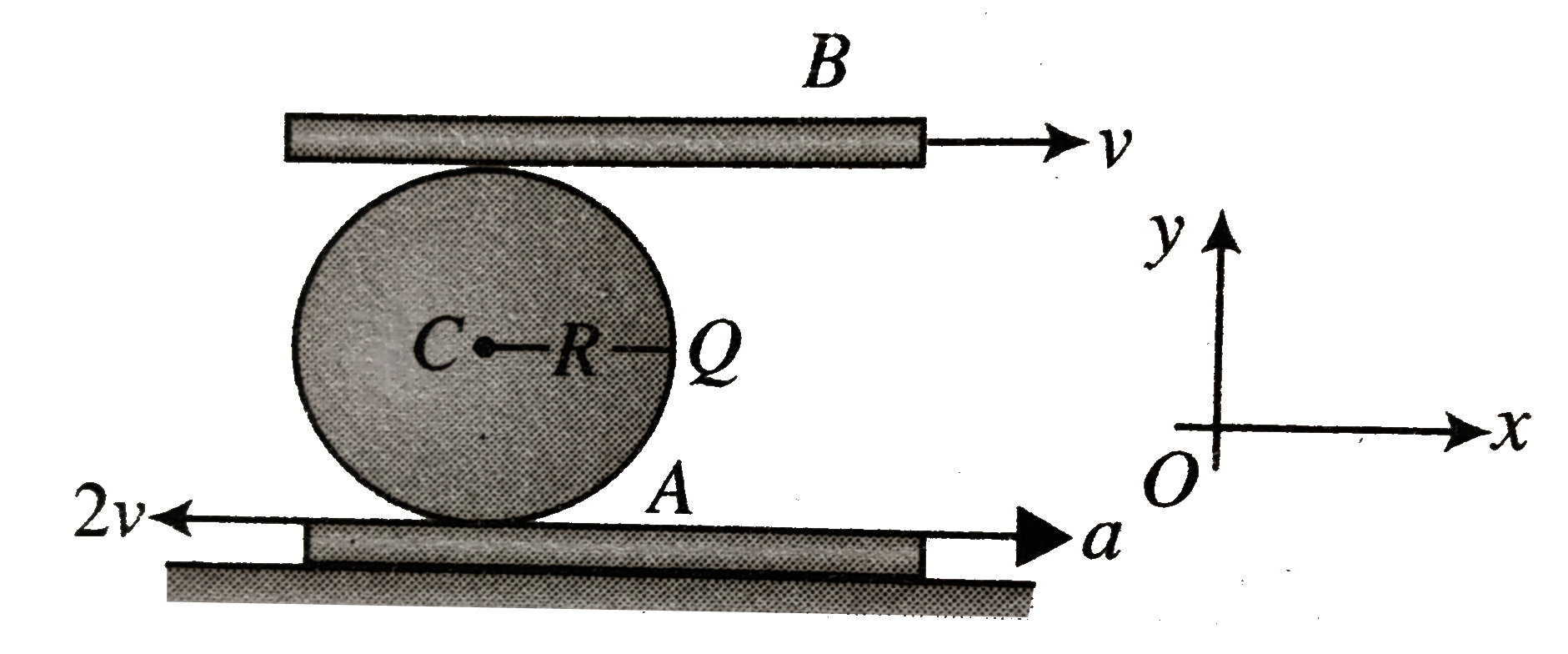


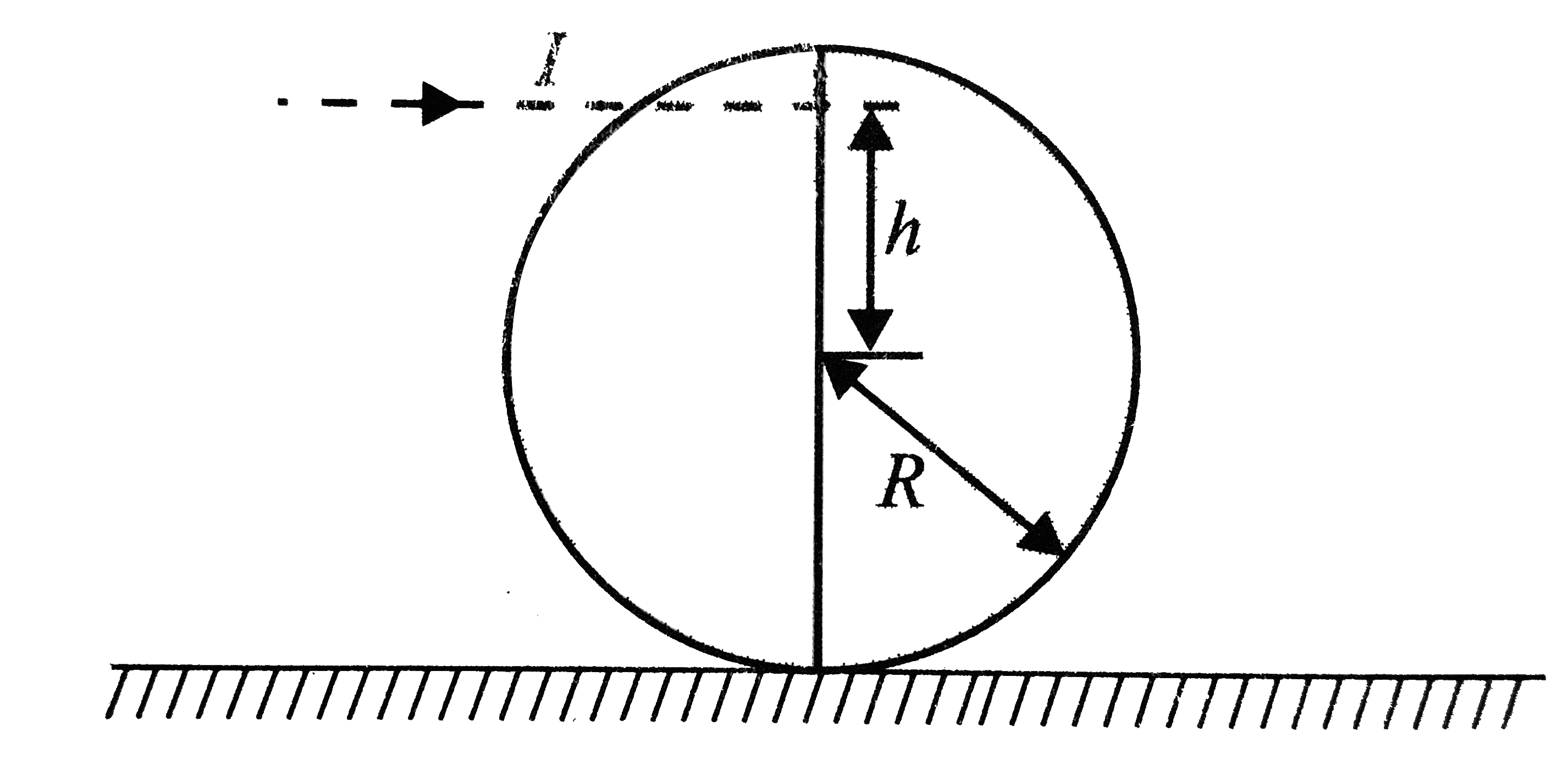

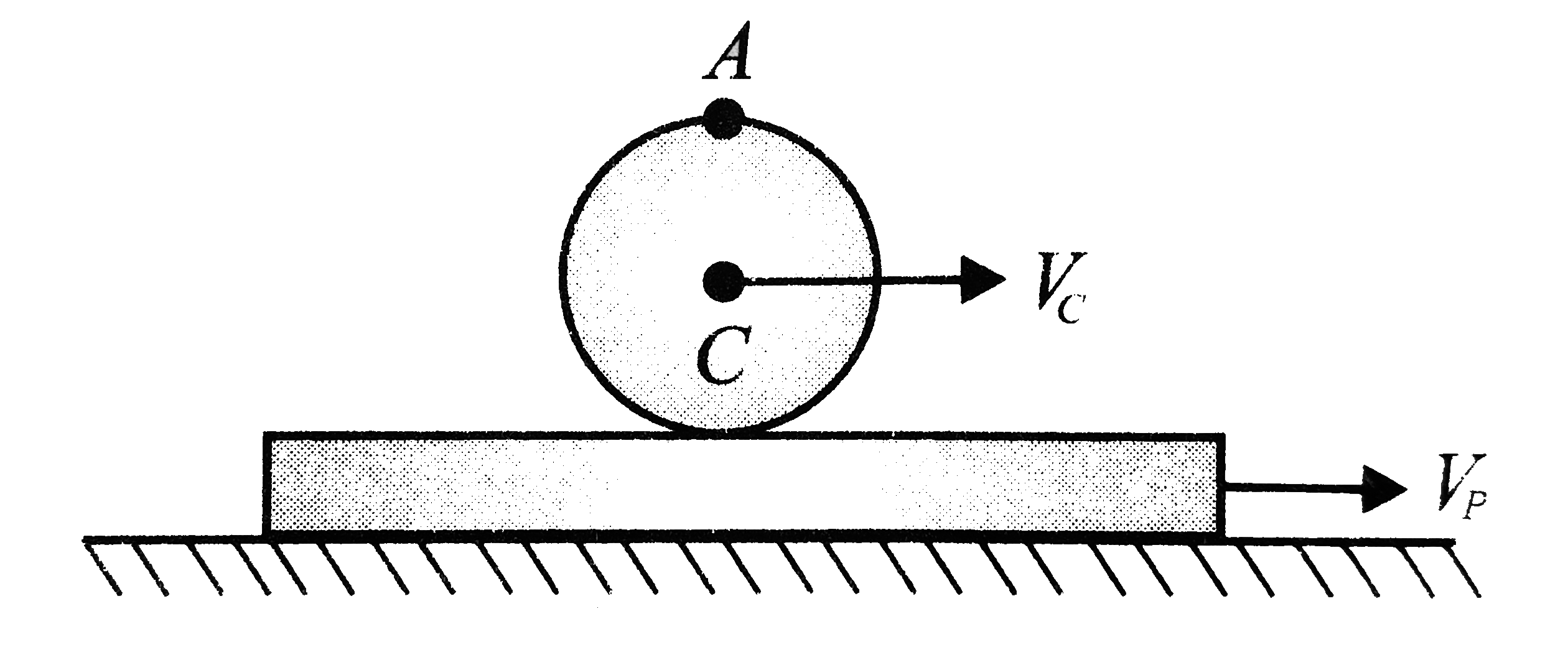




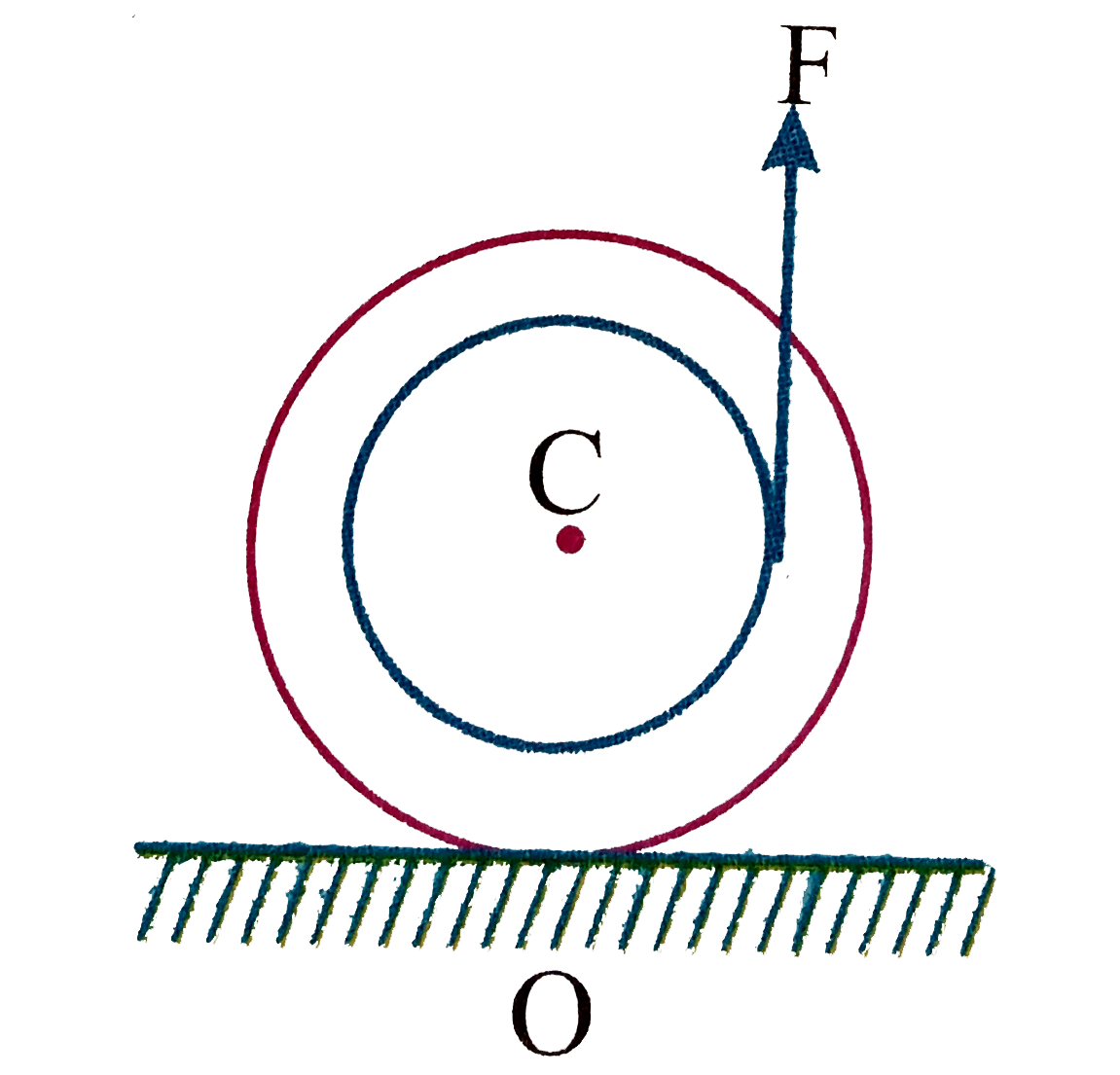




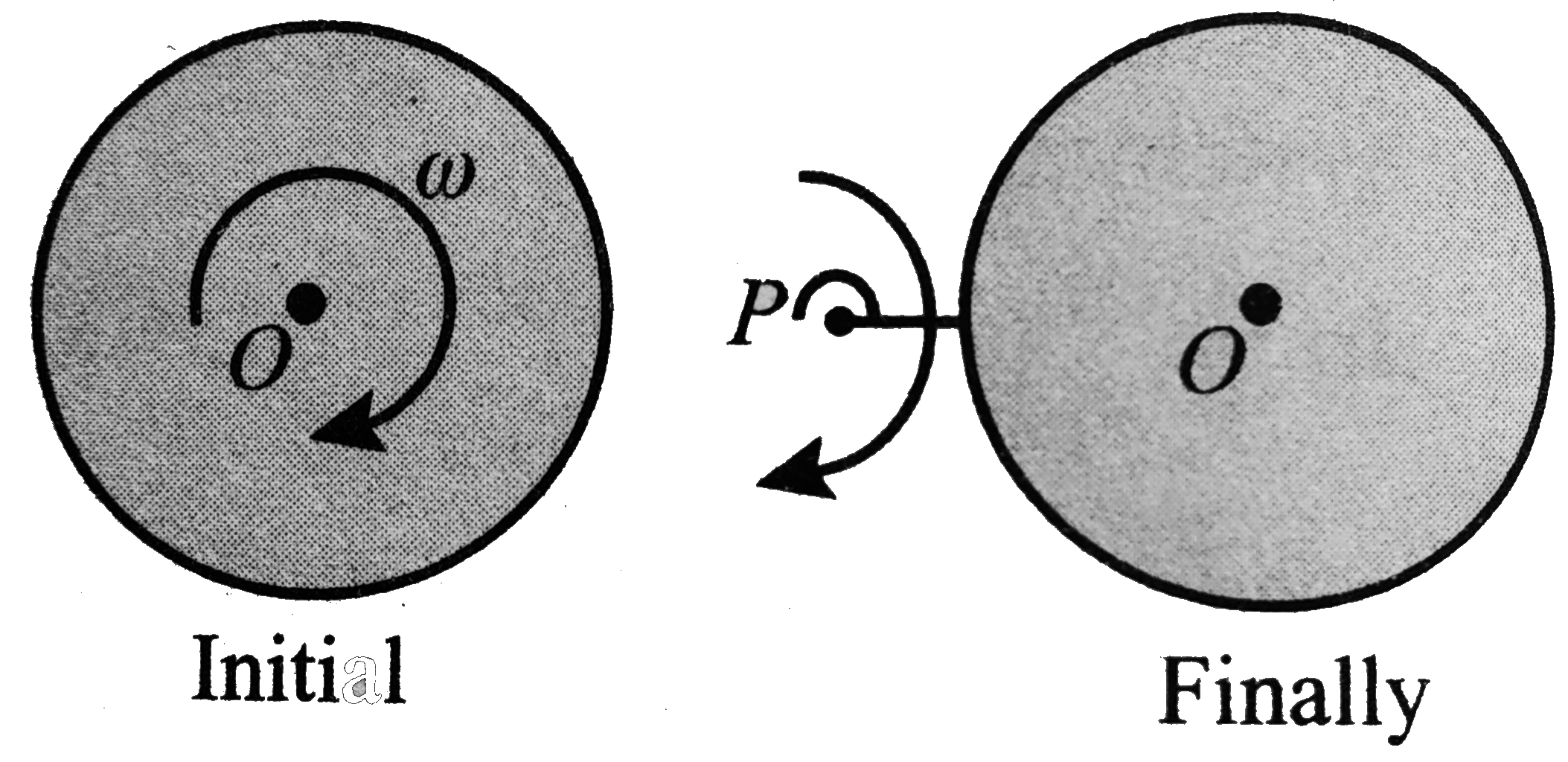
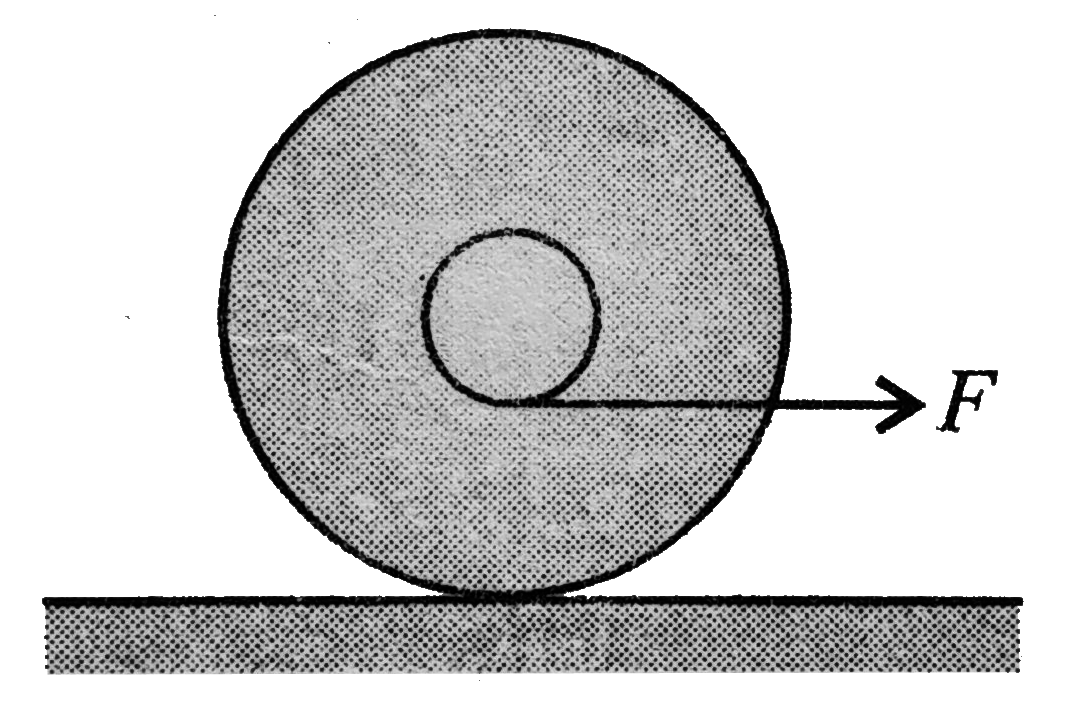


 .
.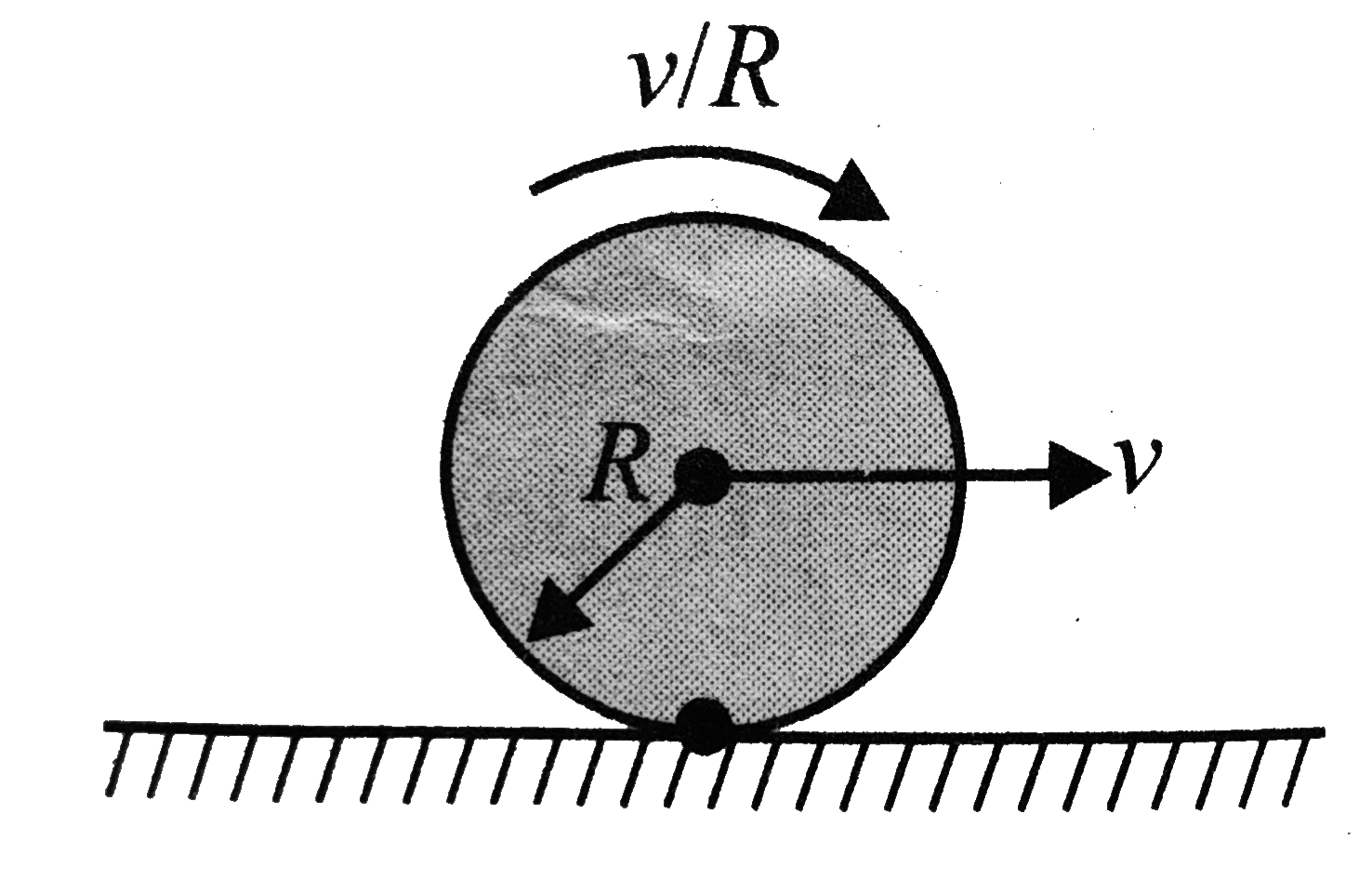



 .
. .
.

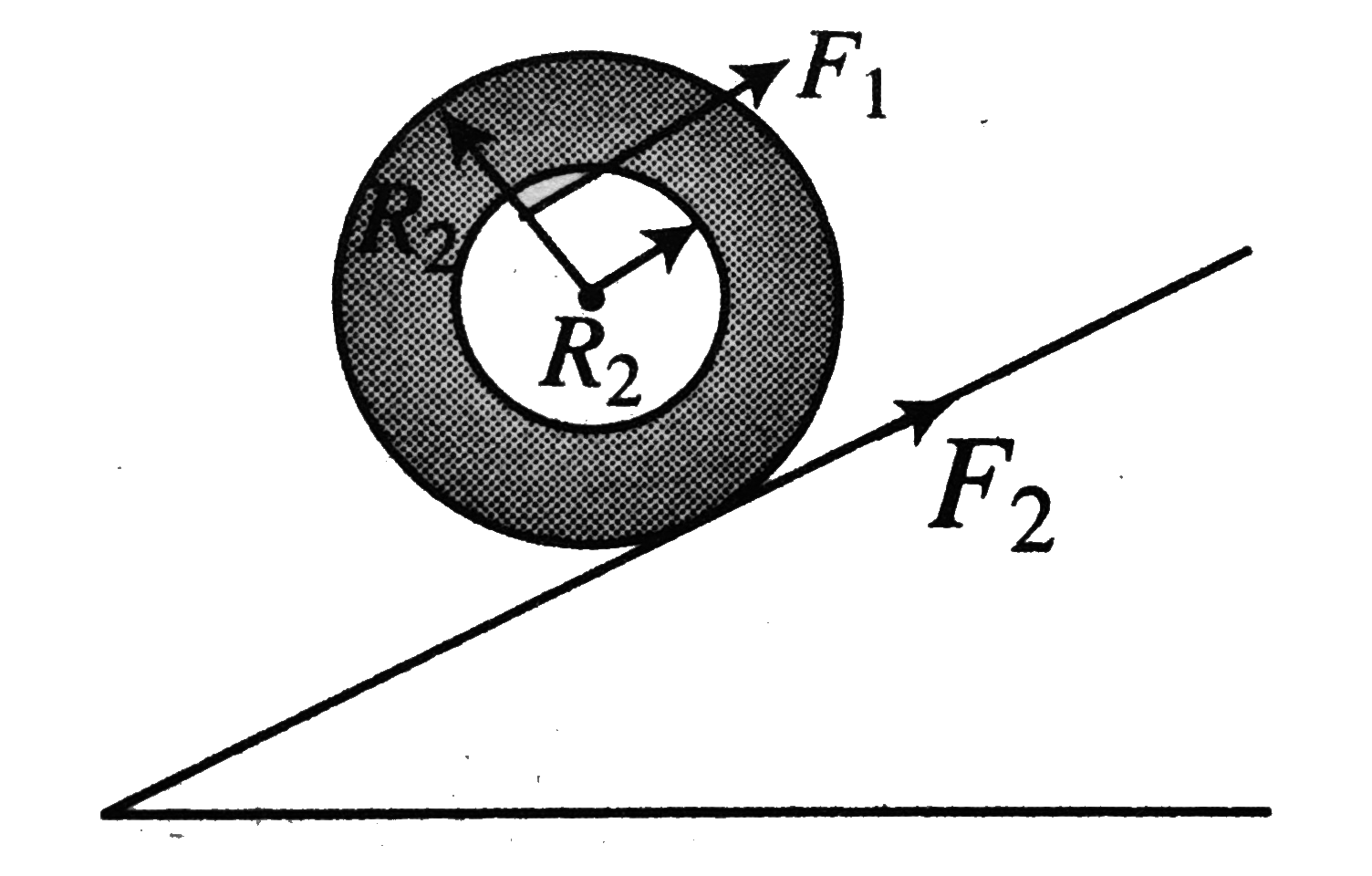
 .
. .
.


 .
.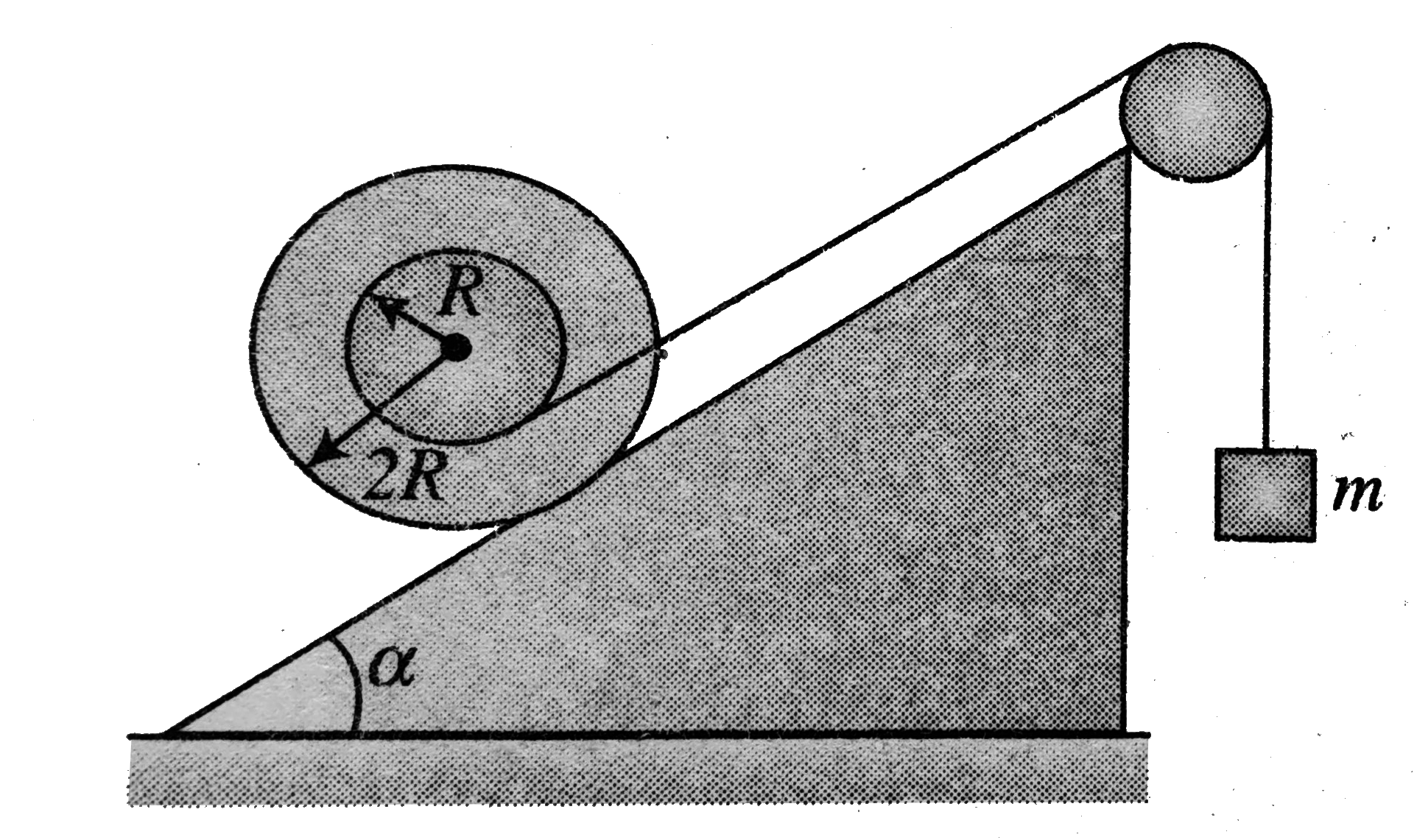
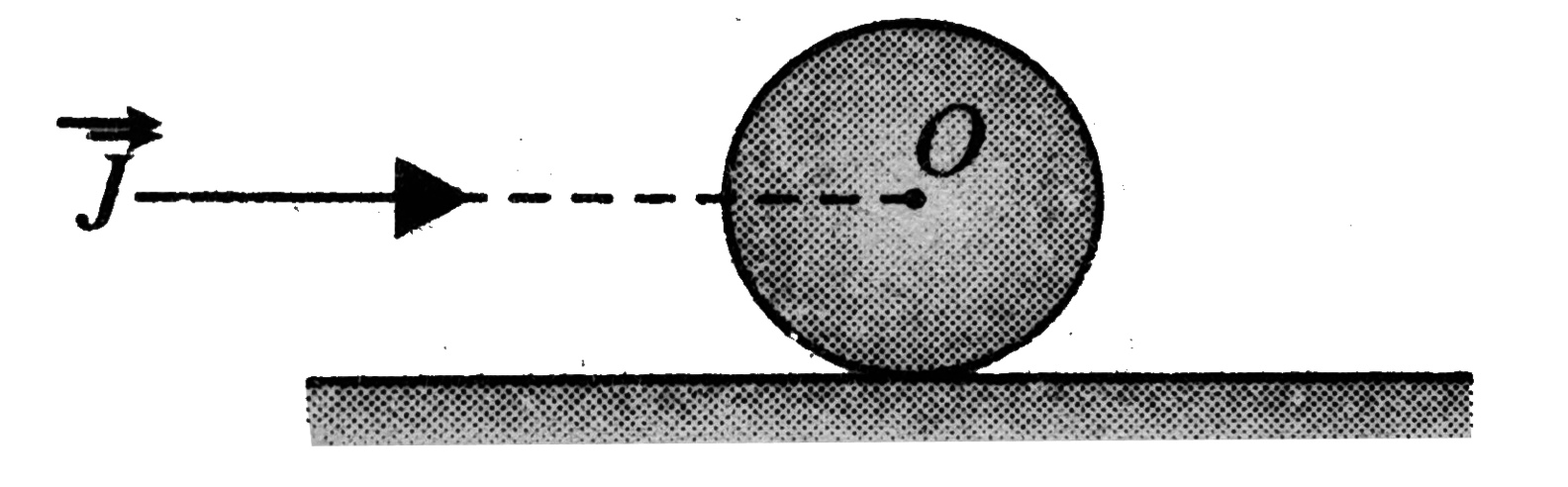
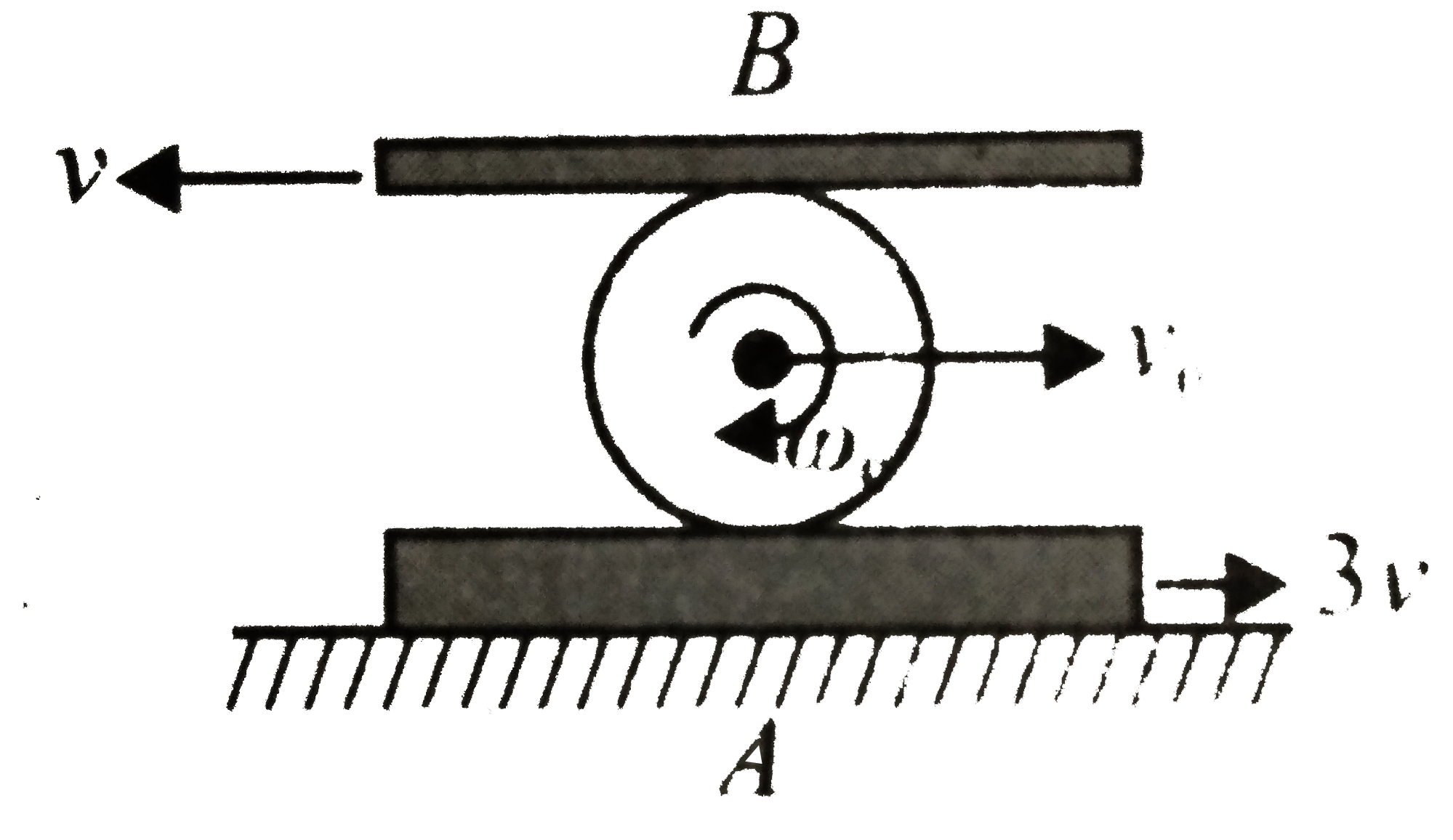


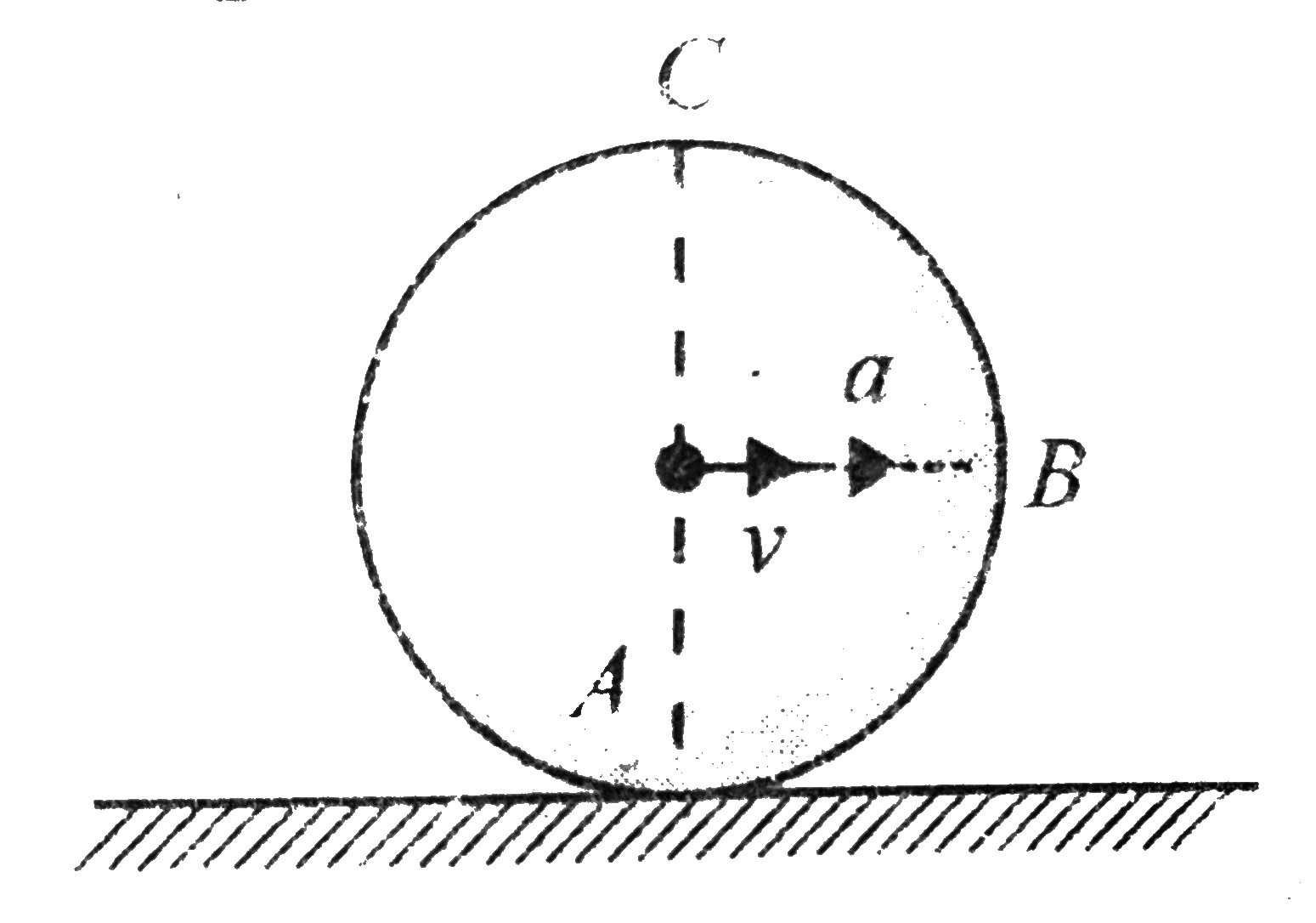

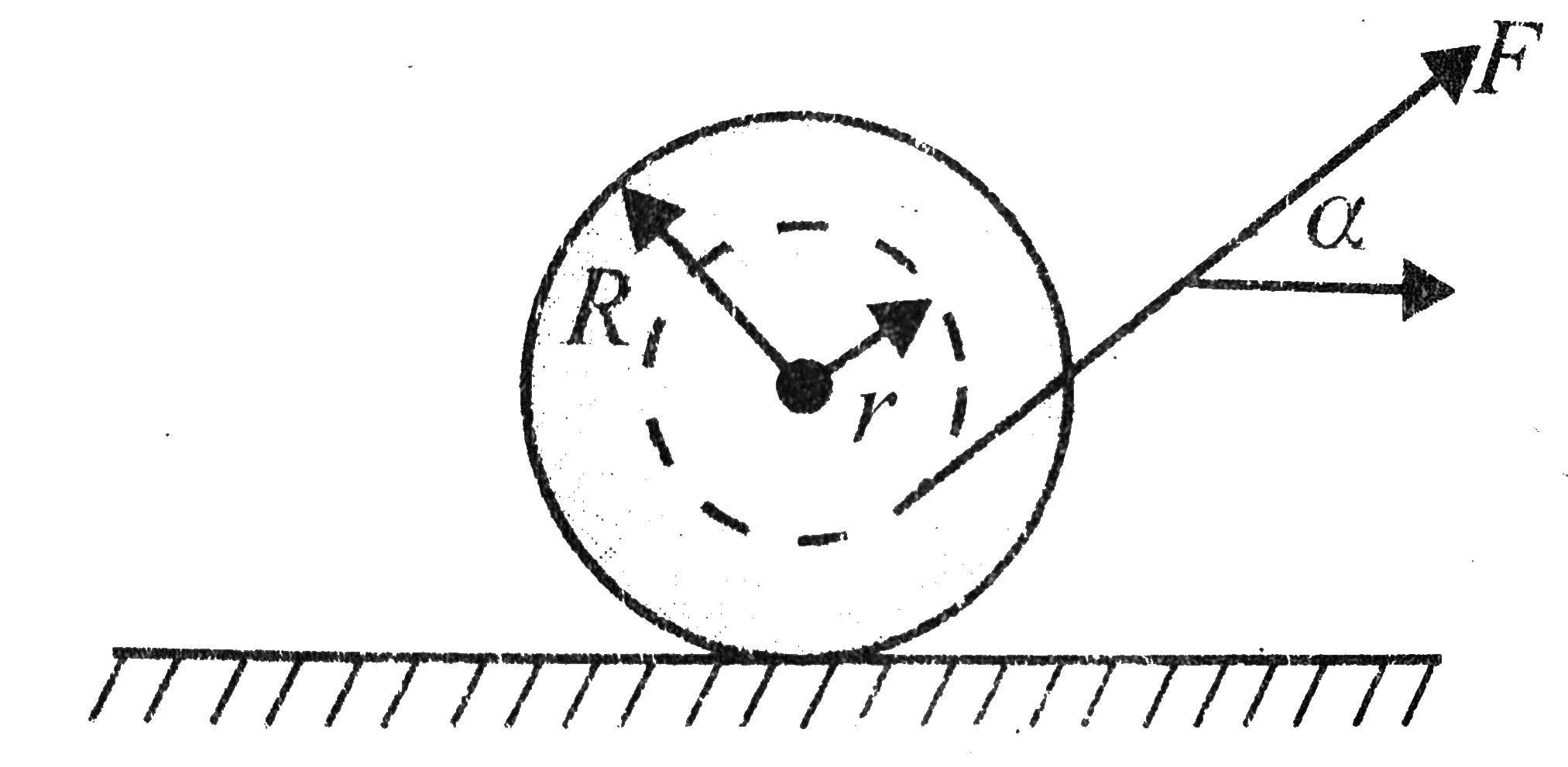



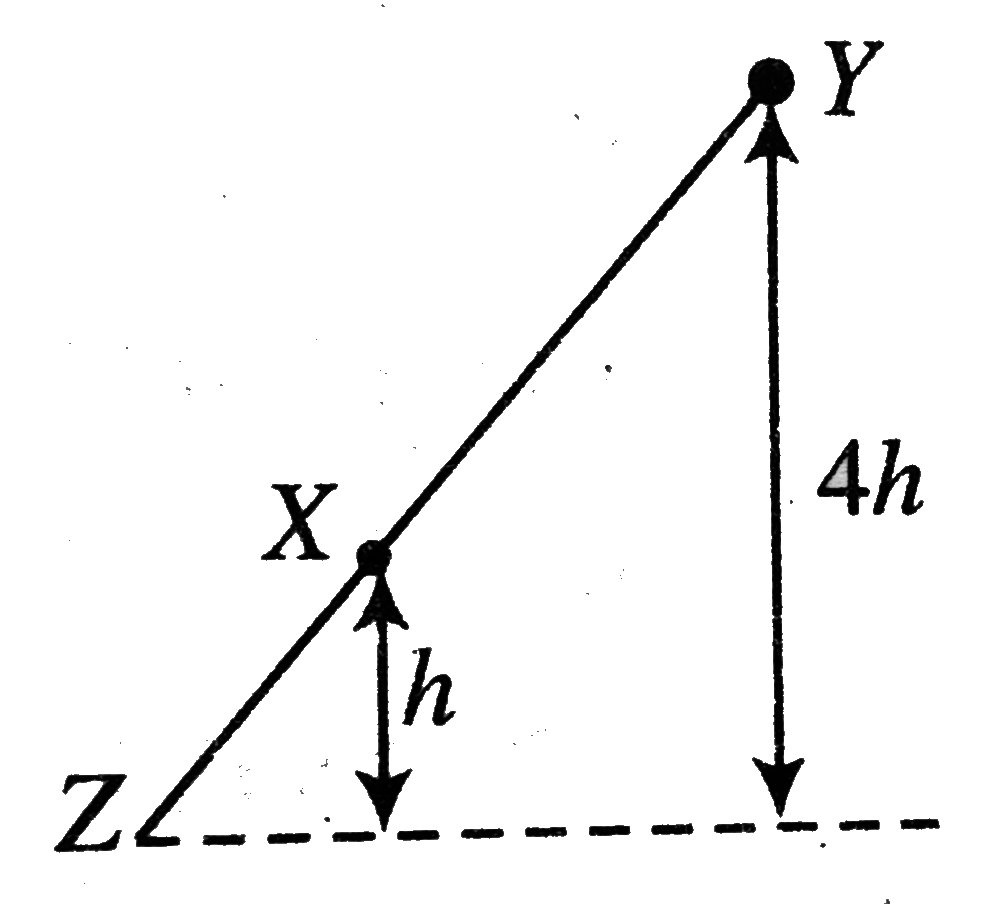



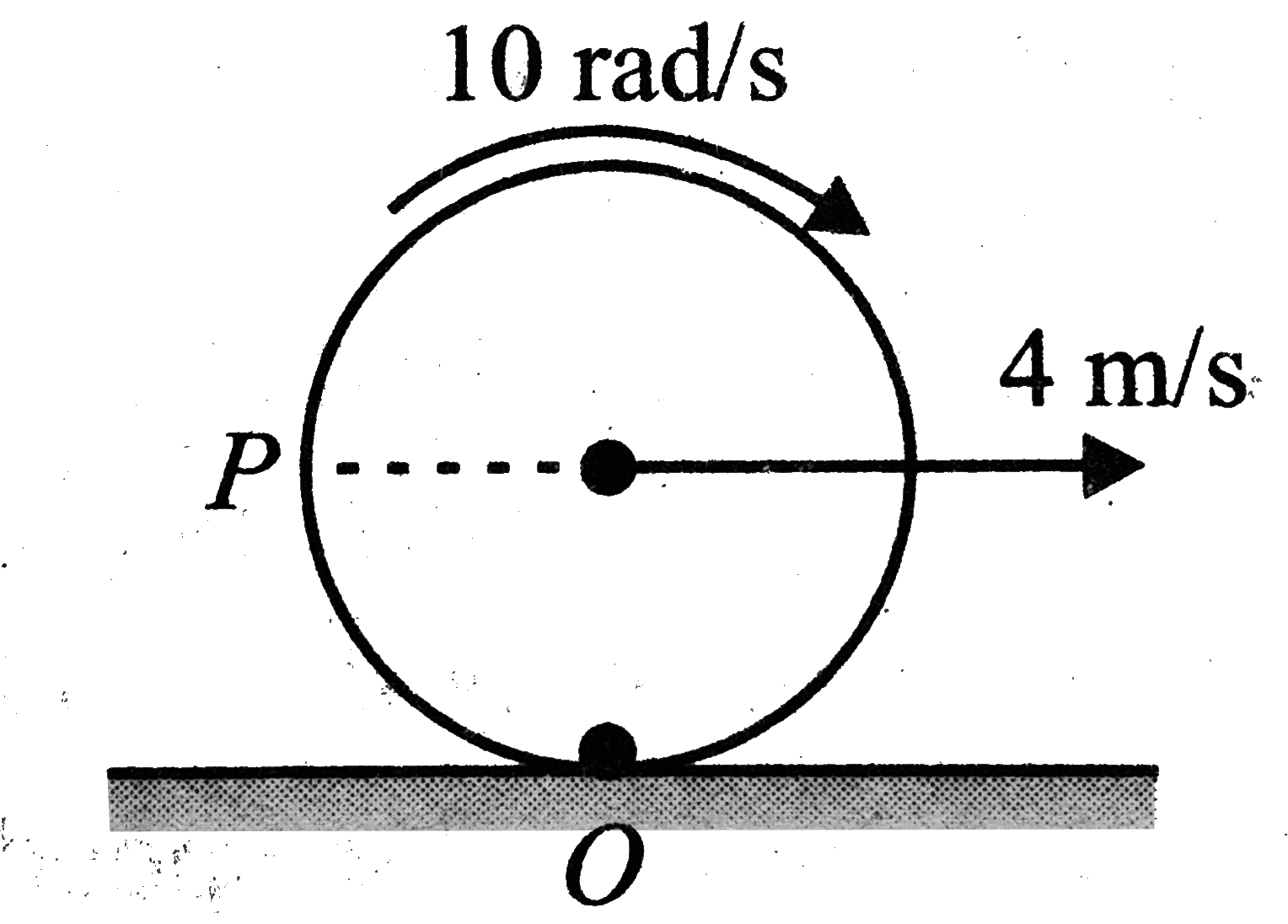
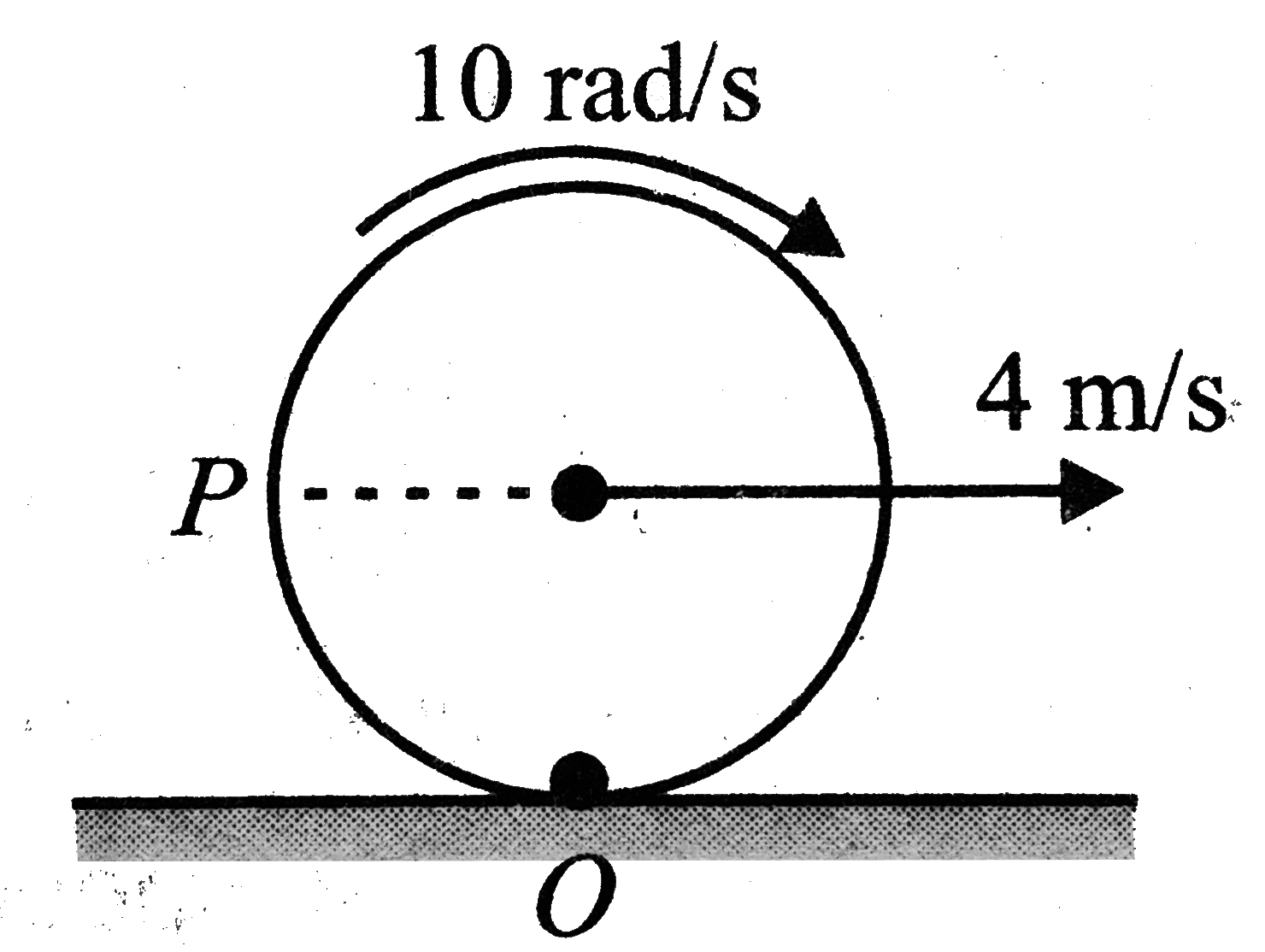


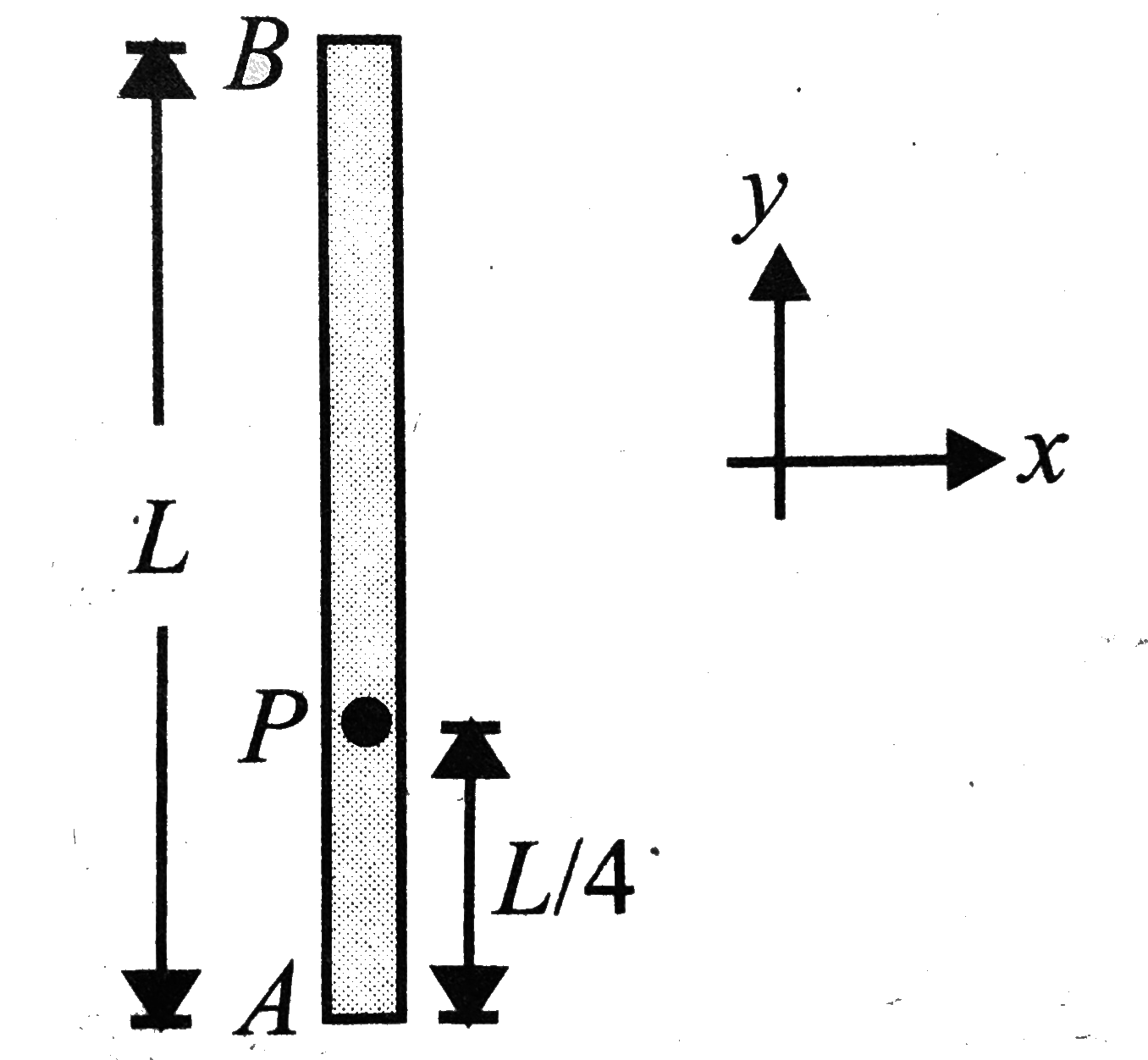
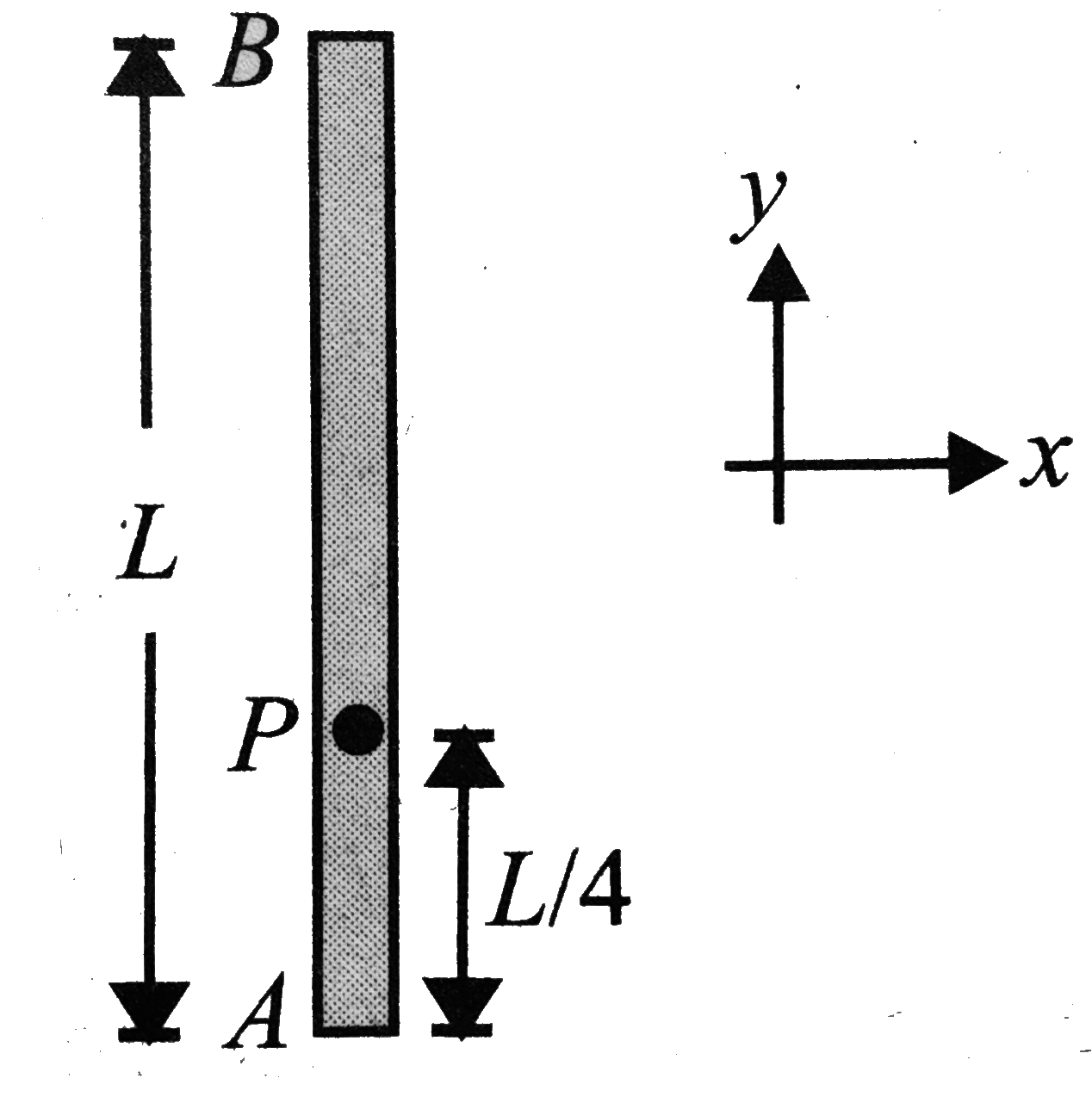
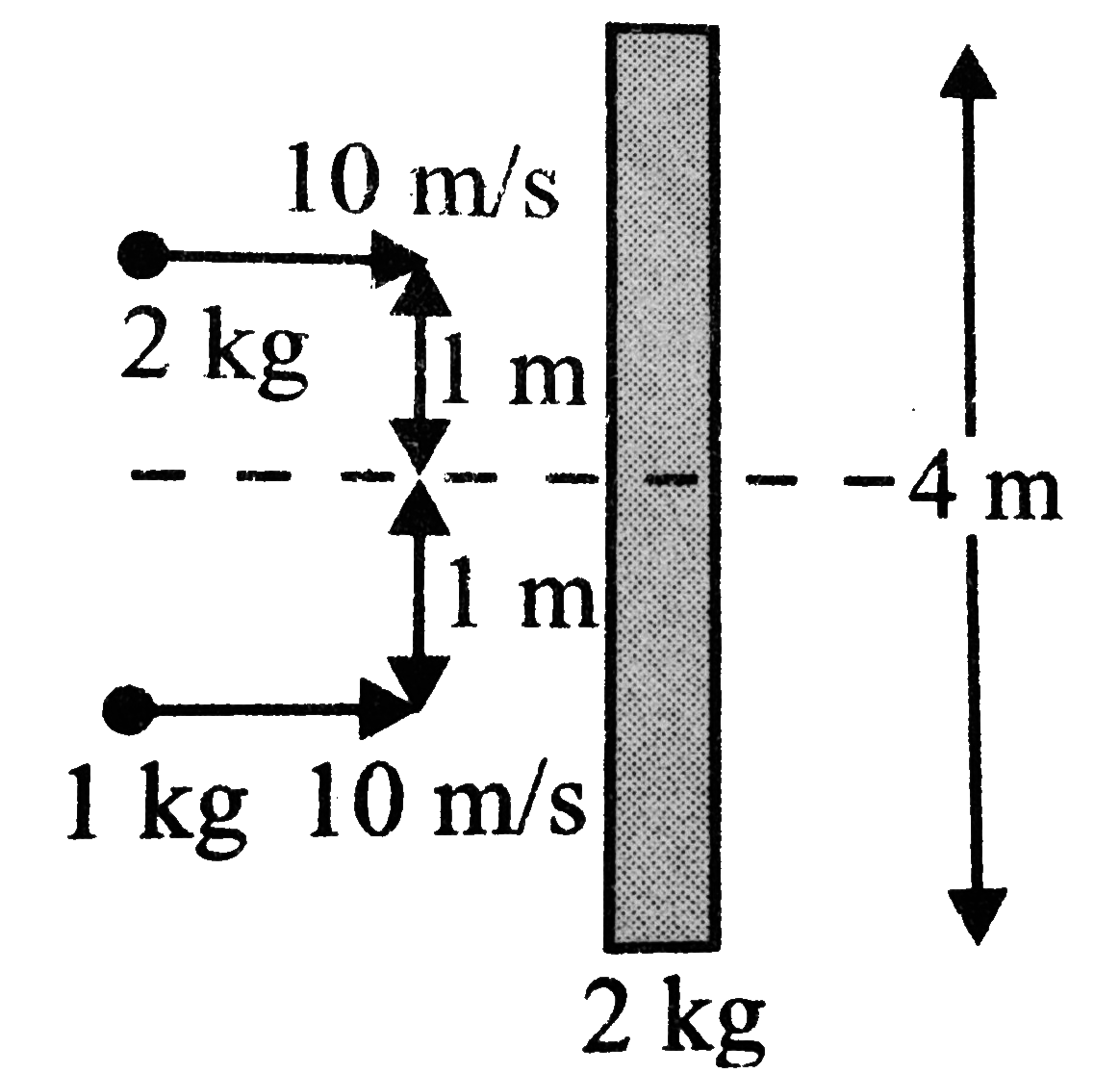
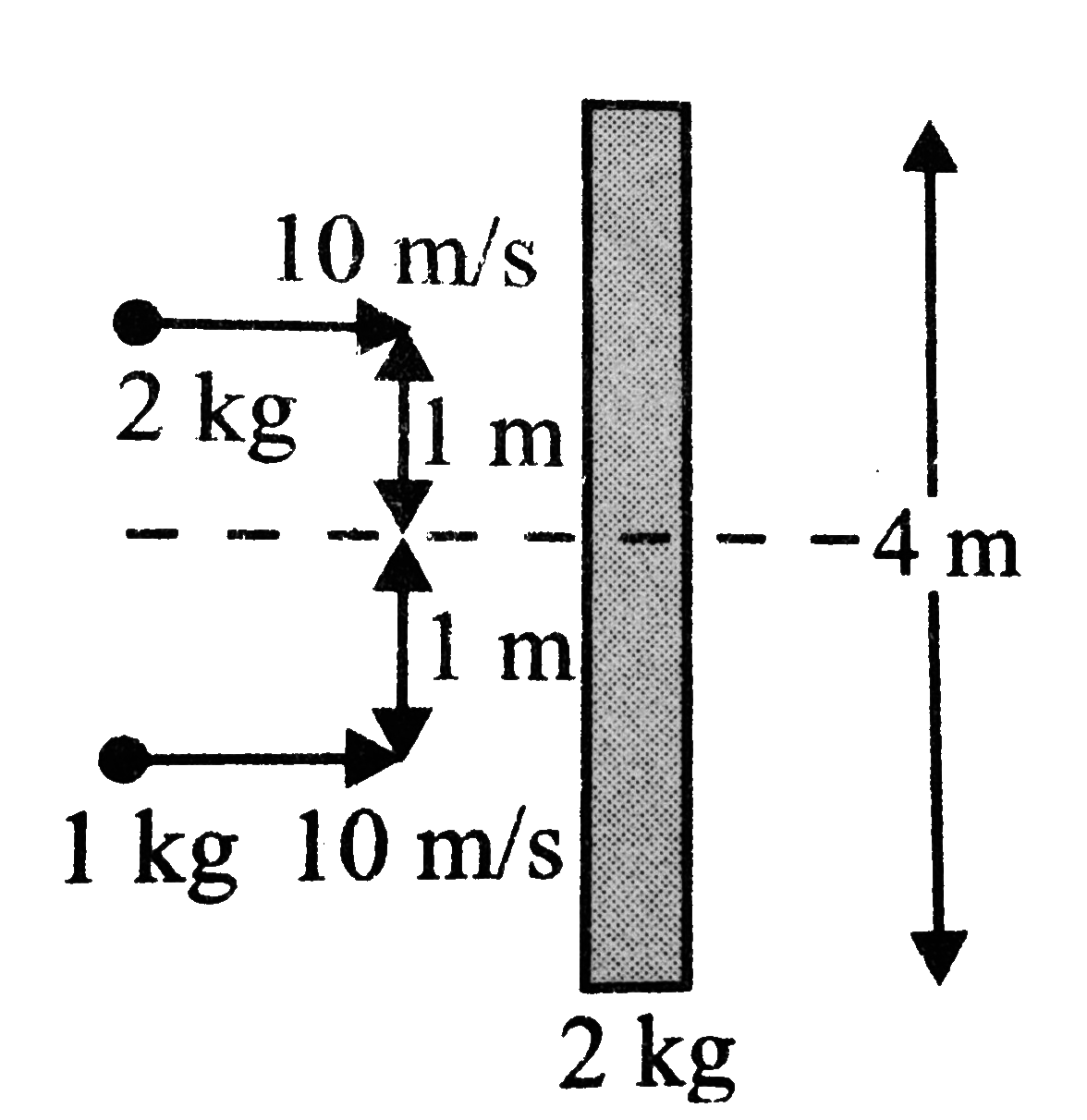
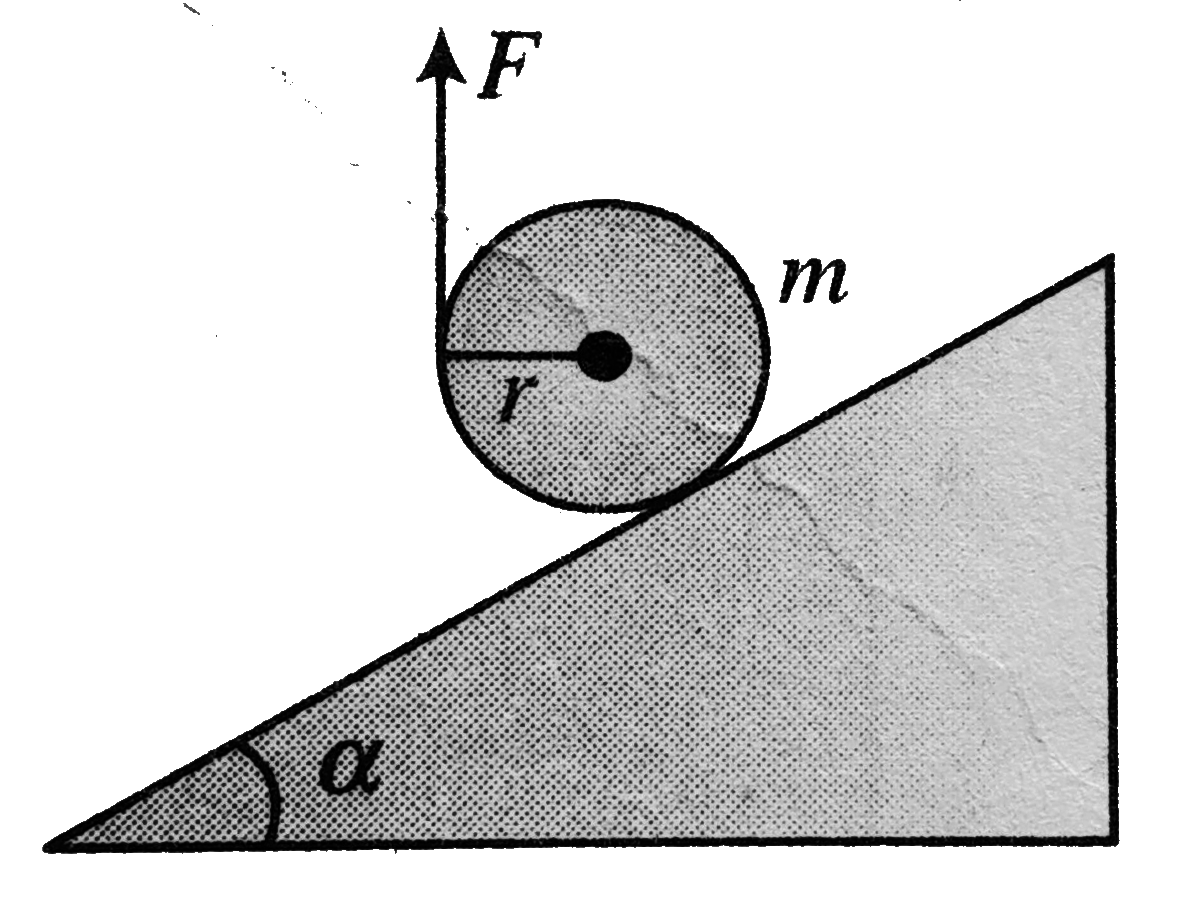



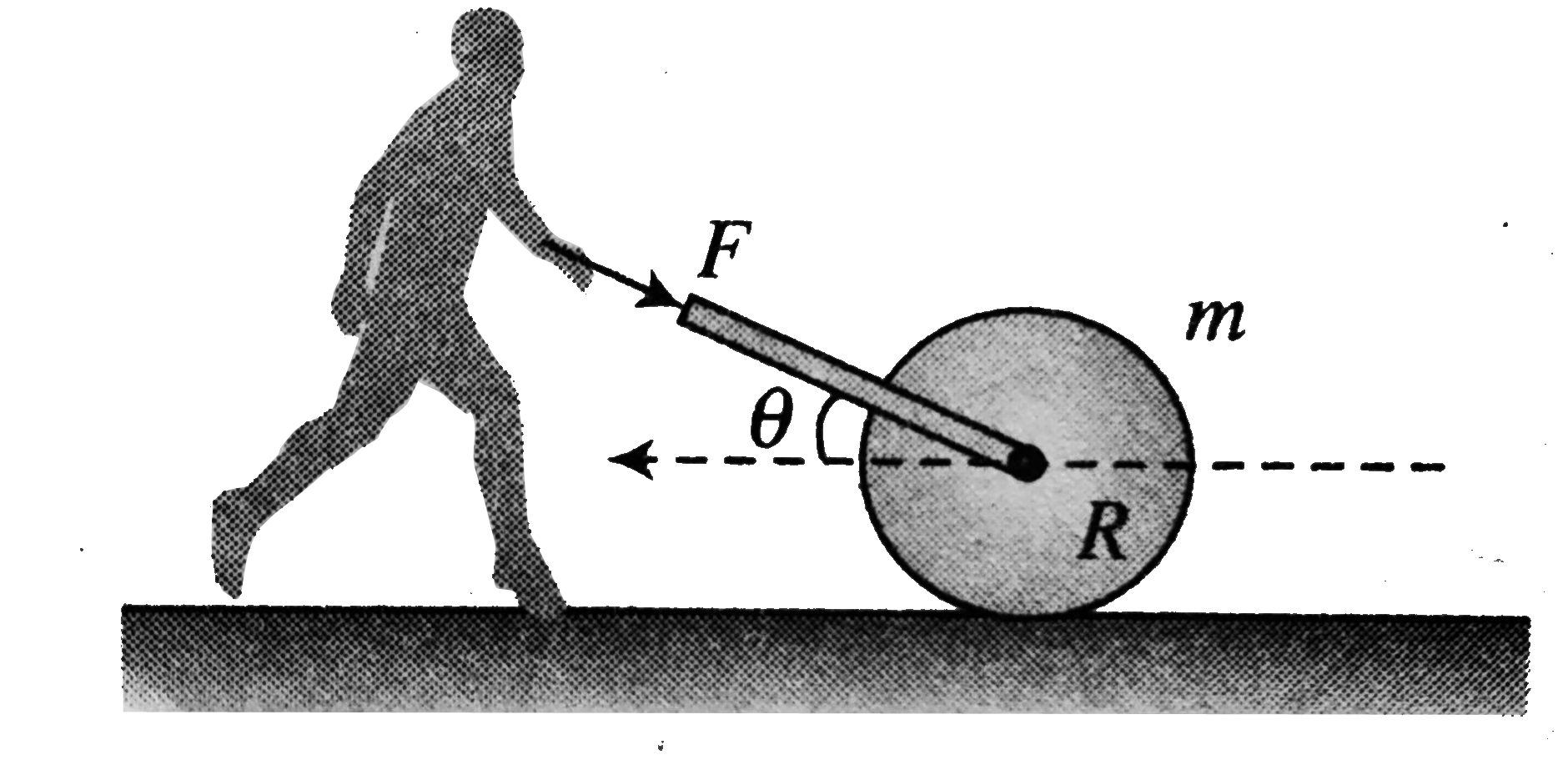
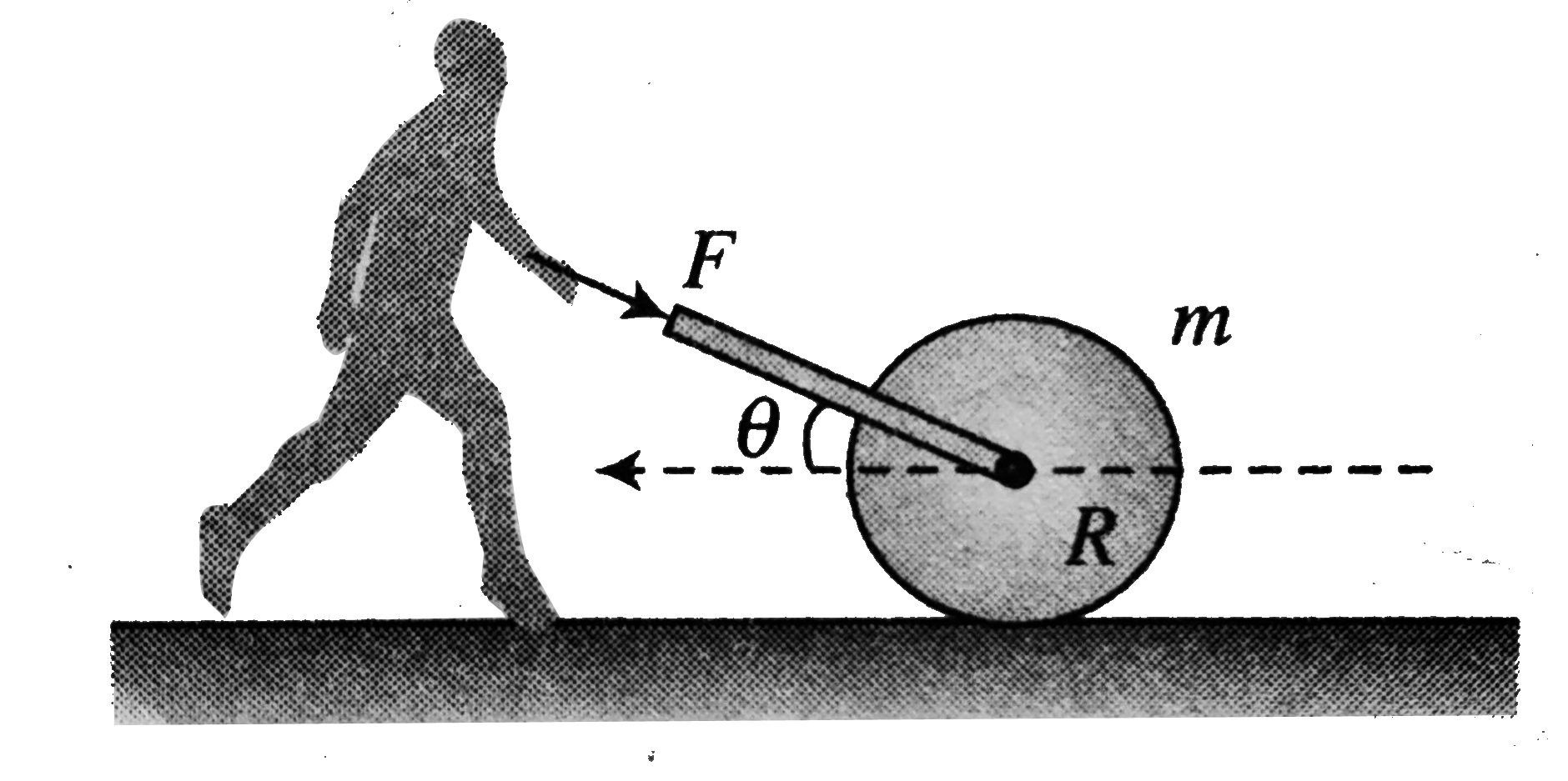


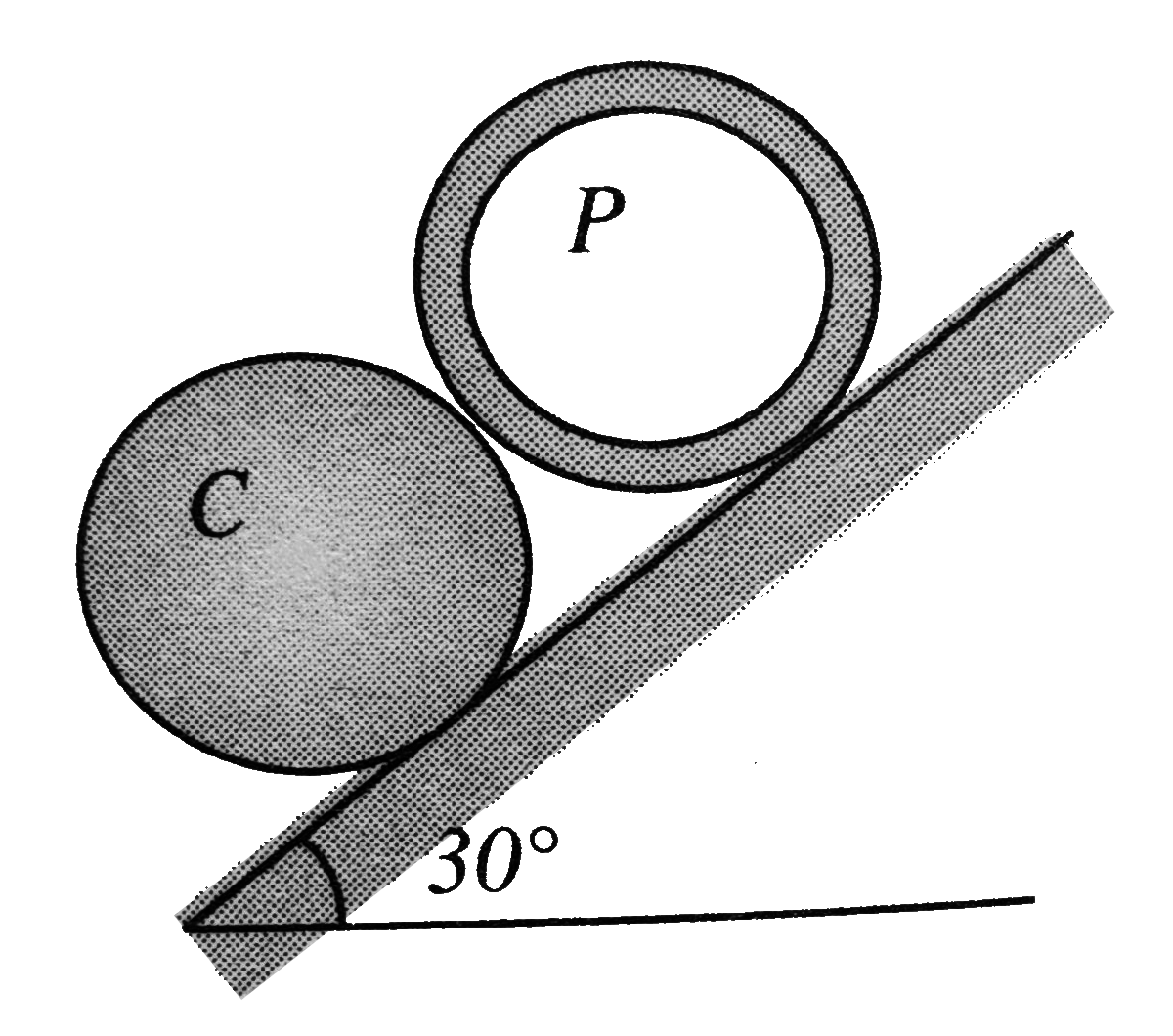

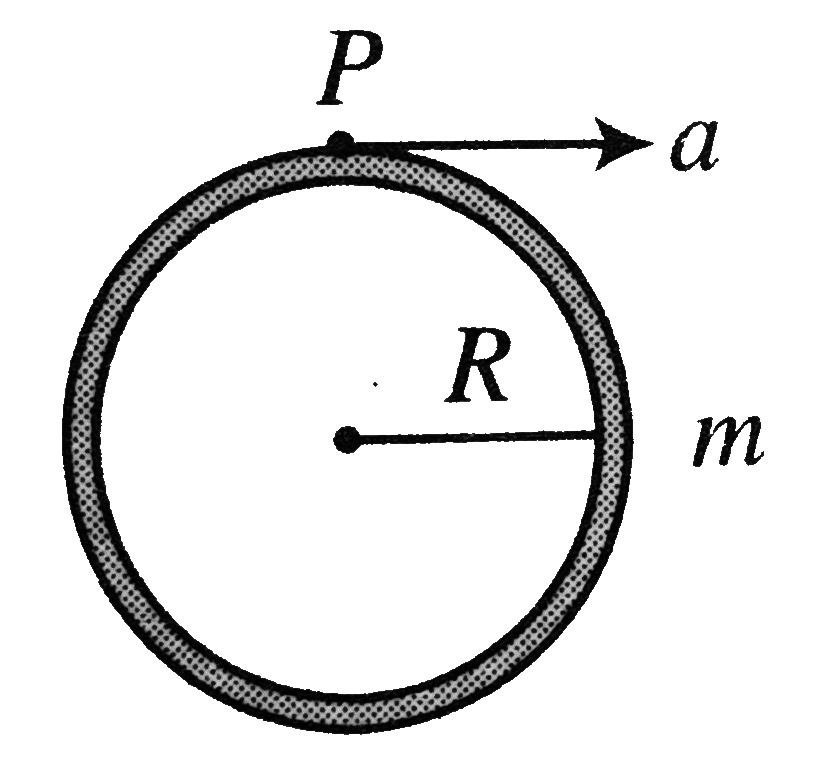

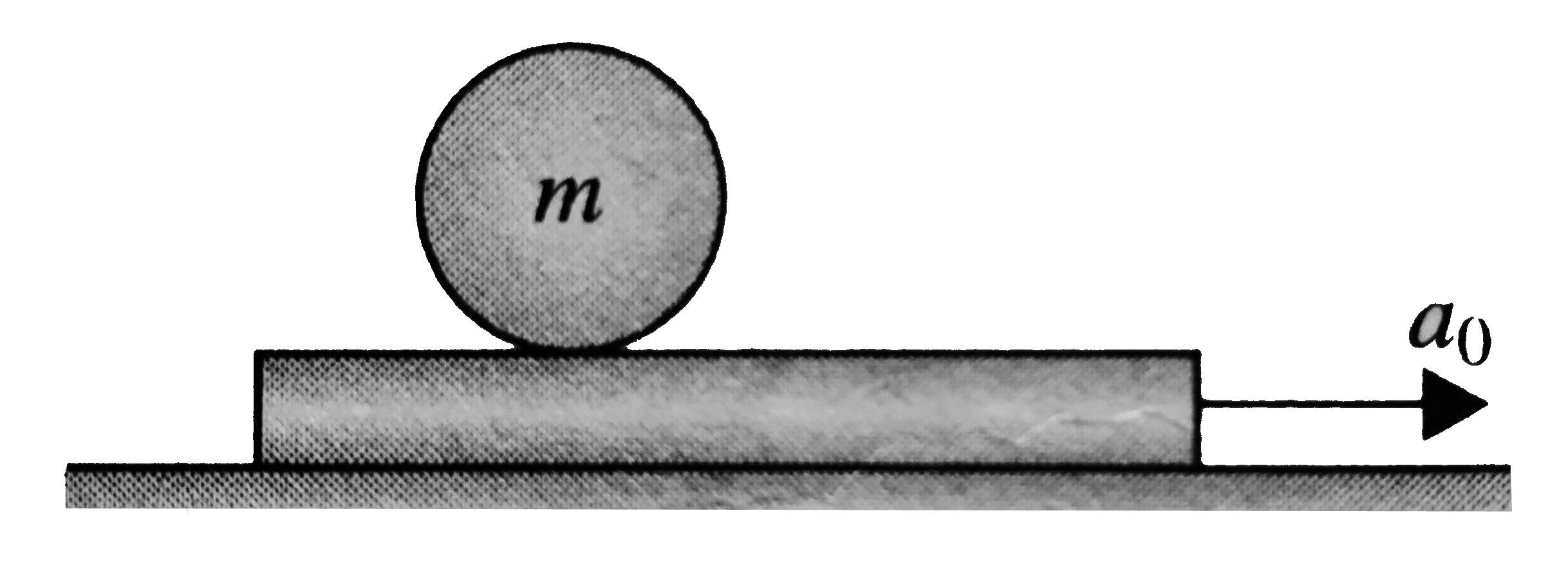
.</a><a href=) View Solution
View Solution .
.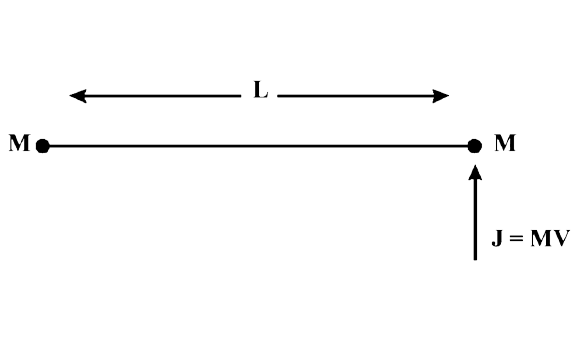
 .
.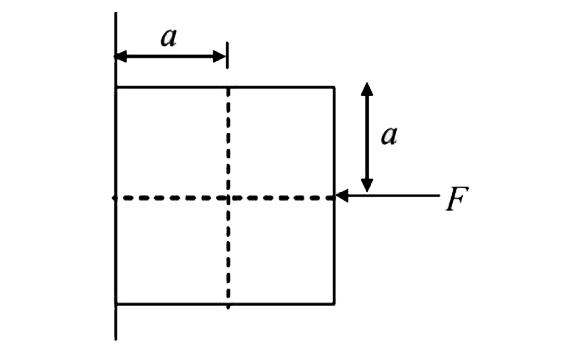

 .
.