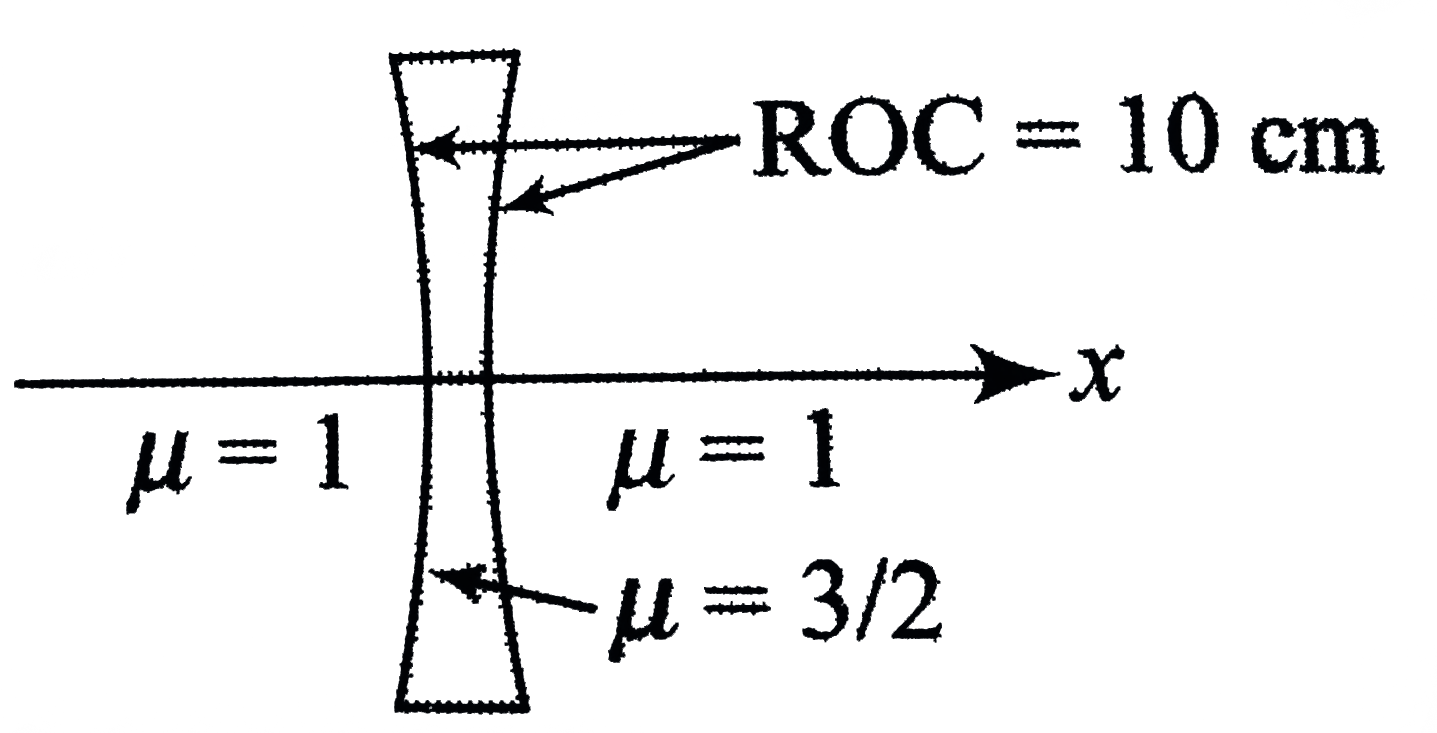LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) STRAIGHT OBJECTIVE TYPE QUESTIONS) from AAKASH SERIES Chapter 18 GEOMETRICAL OPTICS for Class 12
| Class 12 | PHYSICS |
| Chapter | GEOMETRICAL OPTICS |
| AAKASH SERIES | LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) STRAIGHT OBJECTIVE TYPE QUESTIONS) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 6
A thin double convex lens is cut into two equal pieces A and B by a plane containing principal axis. The piece B is further cut into two more pieces pieces C and D by another plane perpendicular to the principal axis. If the focal power of the original lens is P, then thos of A and C areView SolutionQuestion 7
Two plano concave lenses of glass of refractive index 1.5 have radii of curvature 20 cm and 30 cm respectively. They are placed in contact with the curved surface towards each other and the space between them is filled with a liquid of refractive index 5/2. The focal length of the combination is (in cm) View SolutionQuestion 8
The two surfaces of a biconvex lens has same radii of curvatures . This lens is made of glass of refractive index 1.5 and has a focal length of 10 cm in air. The lens is cut into two equal halves along a plane perpendicular to its principal axis to yield two plane - convex lenses. The two pieces are glued such that the convex surfaces touch each other. If this combination lens is immersed in water (refractive index =43 ), its focal length (in cm ) is View SolutionQuestion 9
Two converging glass lenses A and B have focal lengths in the ratio 2:1. The radius of curvature of first surface of lens A is 1/4 th of the second surface where as the radius of curvature of first surface of lens B is twice that of second surface. Then the ratio between the radii of the first surfaces of A and B is View SolutionQuestion 10
Two thin symmetrical lenses of different nature and of different material have equal radii of curvature R=15cm. The lenses are put close together and immersed in water (μw=43). The focal length of the system in water is 30 cm. The difference between refractive indices of the two lenses is View SolutionQuestion 12
A point object O approaches a biconvex lens of focal length 40 cm along its optic axis with a speed of 10 m/s while the later receeds away from the former with a speed of 4 cm/s. Find the speed and direction of motion of the image when the object is at a distance of 60 cm from the lens.
 View Solution
View Solution
All Exercises from AAKASH SERIES Class 12 PHYSICS GEOMETRICAL OPTICS
- ADDITIONAL PRACTICE EXERCISE (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET(ADVANCED) INTEGER TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET(ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET(ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE -I (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE I LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) LINKED COMPREHENSION ANSWER TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) MATRIX MATCHING ANSWER TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORETHAN CORRECT ANSWER TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE II LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE III LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) INTEGER TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) LINKED COMPREHENSION TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) MATRIX MATCHING TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET (EXERCISE-I (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-I (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-I (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-I (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-I (LEVEL-II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-I (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-II (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-III (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-III (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-III (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-III (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-III (LEVEL-II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
- LECTURE SHEET (EXERCISE-III (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- PRACTICE SHEET (ADVANCED) (INTEGER TYPE QUESTIOS)
- PRACTICE SHEET (ADVANCED) (LINKED COMPREHENSION CORRECT TYPE QUESTIOS)
- PRACTICE SHEET (ADVANCED) (MATRIX MATCHING TYPE QUESTIOS)
- PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT TYPE QUESTIOS)
- PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIOS)
- PRACTICE SHEET (EXERCISE I LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE II LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE II LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE II LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE II LEVEL -II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE II LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE III LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERICSE-I (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-I (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-I (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-I (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-I (LEVEL-II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-I (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-II (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-II (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-II (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-II (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-II (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
- PRACTICE SHEET (EXERICSE-III (LEVEL-I (MAIN) )
- PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS ))
- PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS ))
- PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ))
- PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS ))