Anti symmetric relation: Definition
What is Anti Symmetric Relation: Definition
Here, we will study about Antisymmetric Relation. In Mathematics, your teacher might have given you to work on a mathematical concept called relations. A relation is a set of ordered pairs, (x, y), where x is related to y by some rule.
Consider the relation 'is divisible by' over the integers. Call it relation R. This relation would consist of ordered pairs, (x,y), such that x and y are integers, and x is divisible by y. Now, consider the teacher's facts again. By fact 1, the ordered pair (number of cookies, number of students) would be in R, and by fact 2, the ordered pair (number of students, number of cookies) would also be in R.
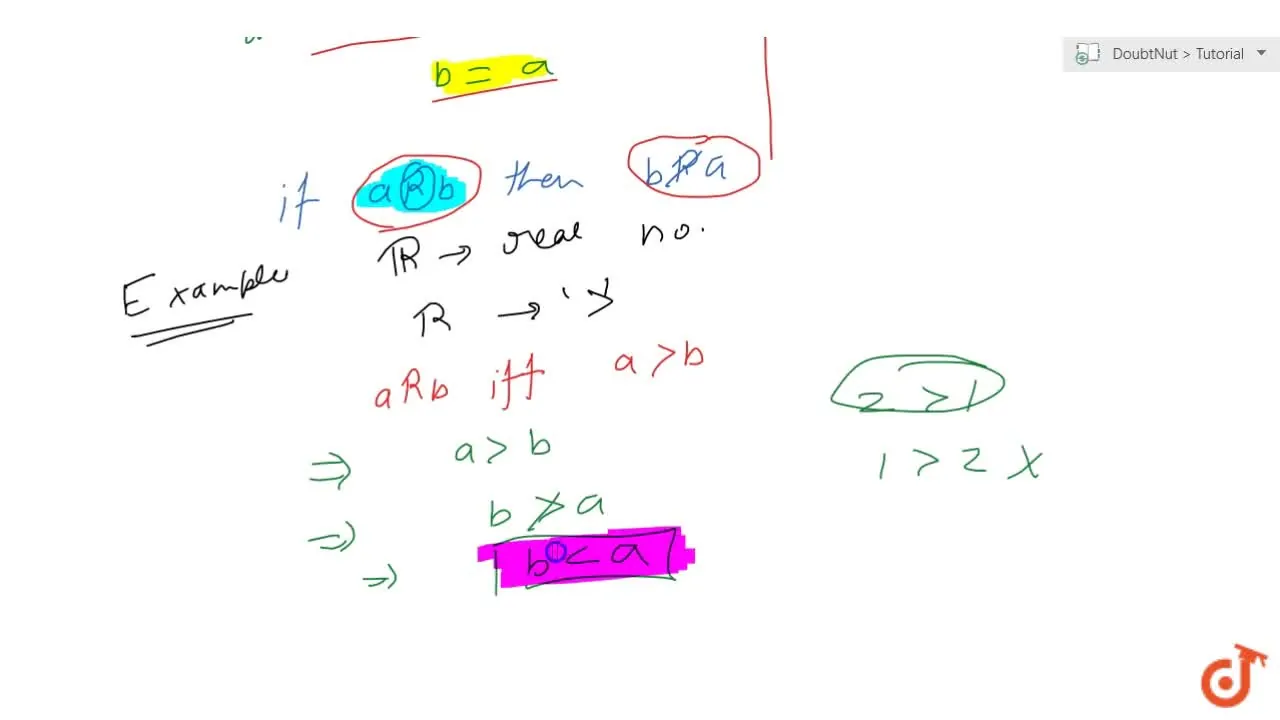
Relations seem pretty straightforward. Let's take things a step further. You see, relations can have certain properties and this lesson is interested in relations that are antisymmetric. An antisymmetric relation satisfies the following property:
If (x, y) is in R and (y, x) is in R, then x =y.
In other words, in an antisymmetric relation, if x is related to y and y is related to x, then it must be the case that x = y.
Now, let's get back to this cookie problem.
As it turns out, the relation 'is divisible by' on the integers is an antisymmetric relation. That is, if x and y are integers, and x is divisible by y and y is divisible by x, it must be the case that x = y.
That means that since (number of cookies, number of students) and (number of students, number of cookies) are both in R, it must be the case that the number of cookies equals the number of students. Since there are 24 students in the class, it must be the case that there are 24 cookies!
Proof of Antisymmetric Relations
Now the teacher says that we have to give her justification that the relation 'is divisible by' really is antisymmetric, so that we use our logic to prove that there are 24 cookies.
In order to prove an antisymmetric relation, we assume that (x = y) and (y, x) are in the relation, and then show that x = y. To prove that our relation, R, is antisymmetric, we assume that x is divisible by y and that y is divisible by x, and we show that x=y.
The definition of divisibility states that, since x is divisible by y and y is divisible by x, x divides into y evenly and y divides into x evenly. We take two integers, call them m and n, such that y = xm and x = yn. If we write it out it becomes:
y = xm = (yn) m = y(nm)
Examples of Antisymmetric Relations
Given a set {1,2,3,4}{1,2,3,4}, how is the following relation RR antisymmetric?
R={(1,2),(2,3),(3,4)}
Solution
Let R be the relation
{(1,2),(1,3),(3,1),(1,1),(3,3),(3,2),(1,4),(4,2),(3,4)}{(1,2),(1,3),(3,1),(1,1),(3,3),(3,2),(1,4),(4,2),(3,4)}
First step is to find 2 members in the relation such that (a,b)∈R(a,b)∈R and (b,a)∈R(b,a)∈R. If no such pair exist then your relation is anti-symmetric. If any such pair exist in your relation and a≠b then the relation is not anti-symmetric, otherwise it is anti-symmetric.
(1,3)∈R and (3,1)∈R and 1≠3(1,3)∈R and (3,1)∈R and 1≠3.
Therefore the relation is not anti-symmetric.
Similar Questions
No. of anti symmetric Relation
View SolutionExplain the following (i)Reflexive Relaton (ii) symmetric Relation (iii) Anti- symmetaic relation (iv) transitive relation
View SolutionAssertion and Reason type questions :Consider the following statements, p: Every reflexive relation is a symmetric relation, q: Every anti-symmetric relation is reflexive.Which of the following is/ are true?
View Solutionskew symmetric matrix
View SolutionDefine a symmetric relation.
View SolutionIf R and S are two symmetric relations (not disjoint) on a set A, then the relation R∩S is
View SolutionConsider the following statements:
(i) Every reflexive relation is anti-symmetric.
(ii) Every symmetric relation is anti-symetric which among i and ii is true?View SolutionIf A={1,2,3}, the number of symmetric relations in A is
View SolutionIf RandR' are symmetric relations (not disjoint) on a set A, then the relation R∪R' is (i) Reflexive (ii) Symmetric (iii) Transitive (iv) none of these
View SolutionS is a relation over the set R of all real numbers and it is given by (a, b)∈S⇔ab≥0 . Then, S is symmetric and transitive only reflexive and symmetric only (c) antisymmetric relation (d) an equivalence relation
View Solution