A pin jointed cantilever frame is hinged to a vertical wall at A and E and is loaded as shown in fig. Determine the forces in the member CD CG and FG.
First find the angle HDG Let Angle HDG = θ tan θ = GH/HD = 2/2 = 1Draw a section line which cut the member CD CG and FG Consider RHS portion of the truss as shown in figTaking Moment about point G we get∑MG = 0{Moment of force TFG and TCG is zero}– TCD x 2 + 2 x 2 = 0 TCD = 2KN TensileSince Angle HDG = DGH = HCG = HGC = 45º Now for angle GEK; tan¸ = 2/8 =1/4Angle GEK = 14ºAngle EGK = 76º Now resolved force TFG and TCG asTaking Moment about point C we get∑MC = 0{Moment of force TCD is zero } – TCG cos 45º x 2 + TCG sin 45º x 2 – TFG sin 76º x 2 – TFG sin 76º x 2 + 2 x 4 = 0– 2 TFG sin 76º + cos 76º + 8 = 0TFG = 3.29KN TensileTaking Moment about point E we get∑ME = 0{Moment of force TFG is zero} – TCD x 4 + 2 x 10 – TCG cos 45º x 8 – TCG sin 45º x 2 = 0– 2 x 4 + 20 -10 TCG cos 45º = 0TCG = 1.69KN Tensile.
Related Solutions
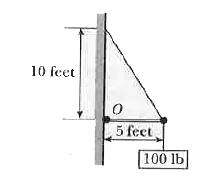
A massless horizontal strut is attached to the wall at the hinge O as shown in the following figure. Which one of the following phrases best describes the force that the hinge pin applies to the strut if the weight of the cables is also neglected ?
 View Solution
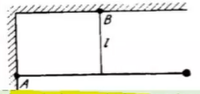
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Vertical component of the force applied by the hinge Vertical component of the force applied by the hinge
View SolutionFour weightless rods of length l each are connected by hinged joints and form a rhomb (Fig). A hinge A is fixed, and a load is suspended to a hinge C. Hinges D and B are connected by a weightless spring of length 1.5l in the undeformed state. In equilibrium, the rods form angles alpha_(0) = 30^(@) with the vertical. Determine the period T of small oscillations of the load.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).

The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).

The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.View Solutionটীকা লেখাে—হিঞ্জ বা কবজা সন্ধি।
View SolutionBall-and-socket joint and hinge joint.
View SolutionBall-and-Socket joint and hinge joint
View SolutionHinge joint is :
View SolutionHinge joint is :
View SolutionHinge joints
View SolutionHINGE JOINTS
View SolutionHinge joints
View SolutionHinge joints
View SolutionHinge joints
View SolutionHinge joints
View SolutionGiven that AB|CD|EF and CE||FG then determine /_EFG
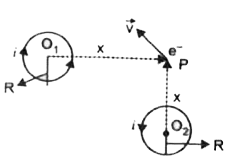
View SolutionThe magnetic force on an at point P as shown in fig . Is :
 View Solution
View SolutionIn the fig. AB||CD. Determine anglex
View Solution
