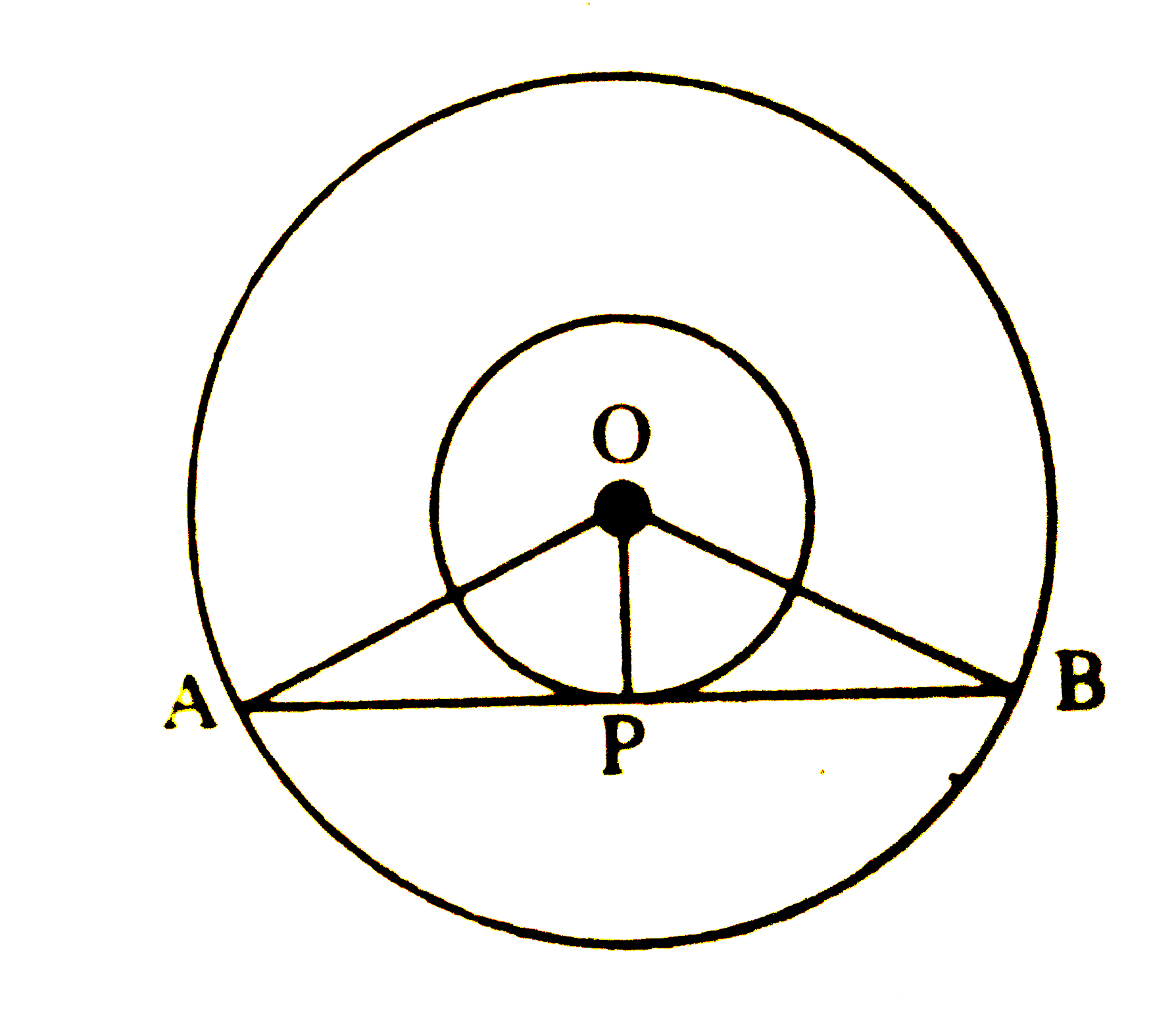
In two concentric circles prove that all chord of the outer circle which touch the inner circle are of equal length.
Consider two concentric circles with centres at O. Let AB and CD be two chords of the outer circle which touch the inner circle at the points M and N respectively.To prove the given question it is sufficient to prove AB = CD.For this join OM ON OB and OD.Let the radius of outer and inner circles be R and r respectively.AB touches the inner circle at M.AB is a tangent to the inner circle
Related Solutions
In two concentric circles prove that all chords of the outer circle which touch the inner circle are of equal length.
View SolutionIn two concentric circles prove that all chords of the outer circle which touch the inner circle are of equal length.
View Solutionसिद्ध करें की दो संकेन्द्रिय वृतों में बाह्म वृत्त की सभी जिवायें जो अन्तः वृत्त को स्पर्श करती हैं, समान लम्बाई की होती हैं|
View SolutionIn two Concentric circles, AB and CD are two chords of the outer circle which touch the inner circle at E and F. Then :
View Solutionदो संकेन्द्रीय वृत्तों में यदि बाहरी वृत्त की ऐसी जीवाएँ खींची गई हैं, जो आन्तरिक वृत्त को स्पर्श करती हैं, तो:
View SolutionTwo concentric circle of radii 3cm and 5cm are given.Then length of chord BC which touches the inner circle at P is equal to
View Solutionचित्र में, 3 सेमी और 5 सेमी त्रिज्या के दो संकेन्द्रित वृत्त है। बाह्रा वृत्त की एक जीवा AB, जो अंतः वृत्त को बिन्दु P पर स्पर्श करती है, की लम्बाई होगी-
 View Solution
View Solutionसिद्ध कीजिए कि दो सकेन्द्रीय वृतों में बड़े वृत्त की वे जीवा जो छोटे वृत्त को स्पर्श करती हैं, समान लम्बाई की होती हैं।
View SolutionOut of two concentric circles, the diameter of the outer circle is 26 cm and the chord MN of length 24 cm is tangent to the inner circle. The radius of the inner circle is
View SolutionIn two concentric circles, the diameter of the outer circle is 26 cm and a chord MN of length 24 cm is tangent to the inner circle. What is the radius of the inner circle?
View Solutionদুটি কেন্দ্রীয় বৃত্তের বড়ো বৃত্তটির দুটি জ্যা ছোটো বৃত্তটিকে স্পর্শ করলে প্রমাণ করো, ওই জ্যা-গুলি সমান দৈর্ঘ্যের হবে।
View SolutionOut of the 2 concentric circle the radius of the outer circle is 5 cm and the chord AC of the length 8 cm is a tangent to the inner circle find the radius of the inner circle
View Solutionयदि दो संकेन्द्रीय वृत्तो की त्रिज्याऍं क्रमश: 4 cm एवं 5 cm है। तो बाह्रा वृत्त की प्रत्येक वह जीवा जो अन्त: वृत्त की स्पर्श रेखा हो लम्बाई होगी।
View SolutionTwo concentric circles are of radii 13 cm and 5 cm. Find the length of the chord of the larger circle which touches the inner circle.
View SolutionTwo concentric circles are of radii 13 cm and 5 cm. Find the length of the chord of the larger circle which touches the inner circle.
View SolutionIn two concentric circles with centre O. PQ is the diameter of outer circle and QS is the tangent line to the inner circle touching it in R and outer circle is S. Find the length of PR, if radii of two circles are 13 cm and 8 cm.
View SolutionTwo concentric circles area of radii 8cm and 5cm. Find the length of the chord of the length circle which touches the smaller circle.
View SolutionProve that in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact.
View SolutionProve that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
View SolutionProve that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
View Solution
