सिद्ध कीजिए कि (cosecθ−cotθ)2=1−cosθ1+cosθ
R.H.S. =1−cosθ1+cosθ=1−cosθ1+cosθ×1−cosθ1−cosθ
=(1−cosθ)21−cos2θ=(1−cosθ)2sin2θ [∵1−cos2θ=sin2θ]
=(1−cosθsinθ)2=(1sinθ−cosθsinθ)2=(cosecθ−cotθ)2=L.H.S.
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.165videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - लघु उत्तरीय प्रश्न87videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - वस्तुनिष्ठ प्रश्न14videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - वस्तुनिष्ठ प्रश्न28videos
त्रिभुज
Similar Questions
दिए गये चित्र से निम्नलिखित के मान ज्ञात कीजिए :
(i) sinC (ii)sinA
(iii) cosC (iv)cosA
(v) tanC (vi)tanA
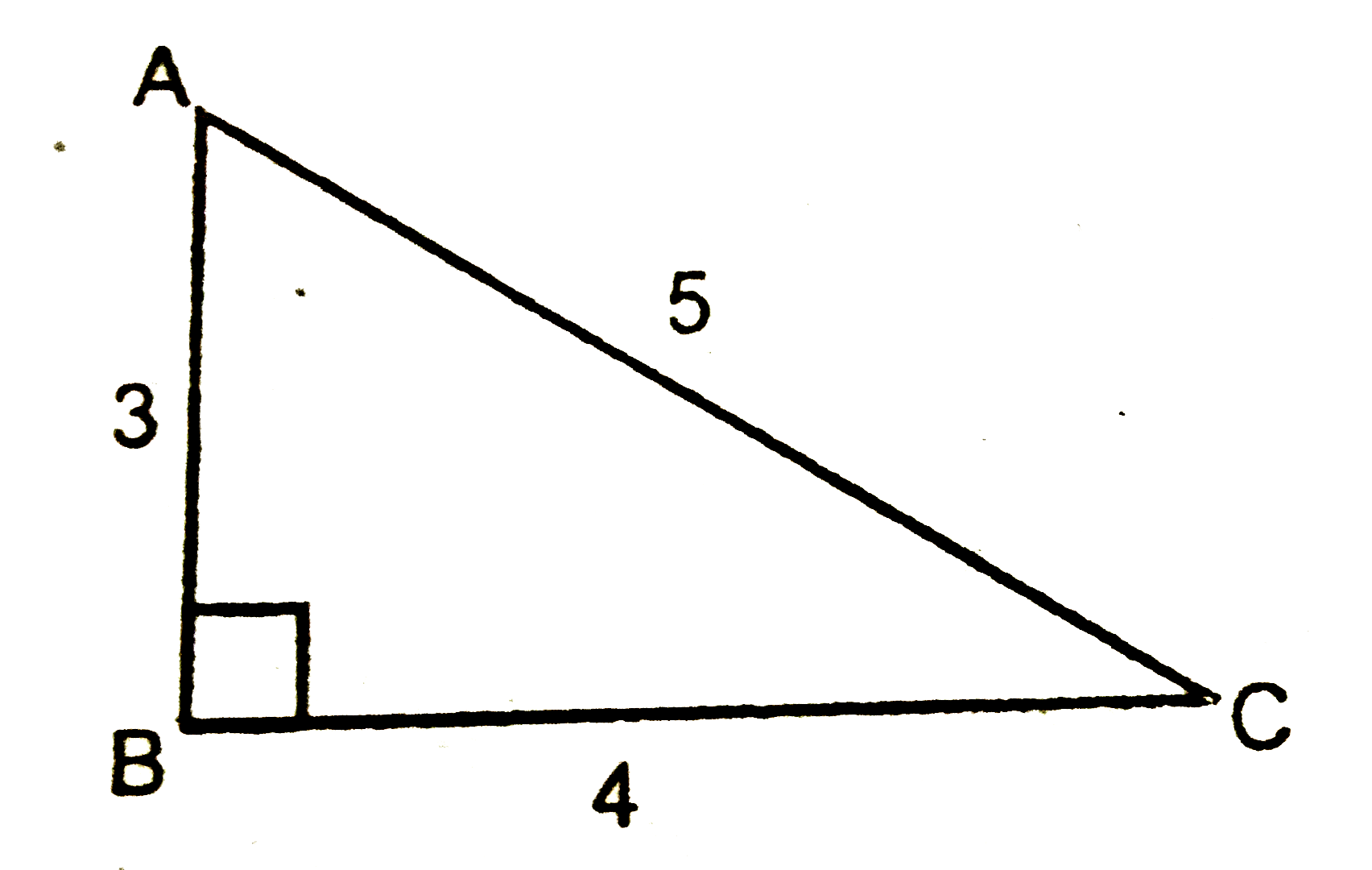 02:09View Solution
02:09View Solutionयदि tanA=ba,जहाँ a और b वास्तविक संख्याएँ है , तो sin2A का मान ज्ञात करें ।
01:03View Solutionयदि एक मीनार के पाद से 100 m दूर स्थित बिंदु पर मीनार का उन्नयन कोण60∘ है , तो मीनार कि ऊँचाई है :
03:38View SolutionΔABC में DE∣∣BC और ADDB=53 तब AEAC=
02:18View Solution(cot theta+csc theta-1)/(cot theta-csc theta+1)=(1+cos theta)/(sin theta)
00:49View Solutioncsc theta(1+cos theta)(csc theta-cot theta)=1
02:58View SolutionProve that
cotθ+cosecθ−1cotθ−cosecθ+1=1+cosθsinθ.01:44View SolutionProve each of the following identities :
(i)(1+cosθ)(1−cosθ)(1+cot2θ)=1
(ii)cosecθ(1+cosθ)(cosecθ−cotθ)=103:36View SolutionProve that (cot theta-cos theta)/(cot theta+cos theta)=(cosec theta-1)/(cosec theta-1)
06:13View Solutionसिद्ध कीजिए cosθ−sinθ+1cosθ+sinθ−1=cosecθ+cotθ
02:10View Solutionसिद्ध कीजिए- cotθ−cosθcotθ+cosθ=cosecθ−1cosecθ+1
03:22View Solutionसिद्ध कीजिए कि
cotθ+cosecθ−1cotθ−cosecθ+1=1+cosθsinθ01:44View SolutionProve that :
tanθ1−cotθ+cotθ1−tanθ=1+cosθcosecθ01:42View Solutionसिद्ध करें कि
11−cosθ−11+cosθ=2cosθsin2θ=2cotθ⋅cosecθ.01:21View Solutionसिद्ध करें कि
1−cosθ1+cosθ=(1−cosθsinθ)2=(cosecθ−cotθ)2.01:49View Solutionபின்வரும் முற்றொருமைகளை நிரூபிக்கவும். cotθ−cosθcotθ+cosθ=cosecθ−1cosecθ+1
01:26View Solution

