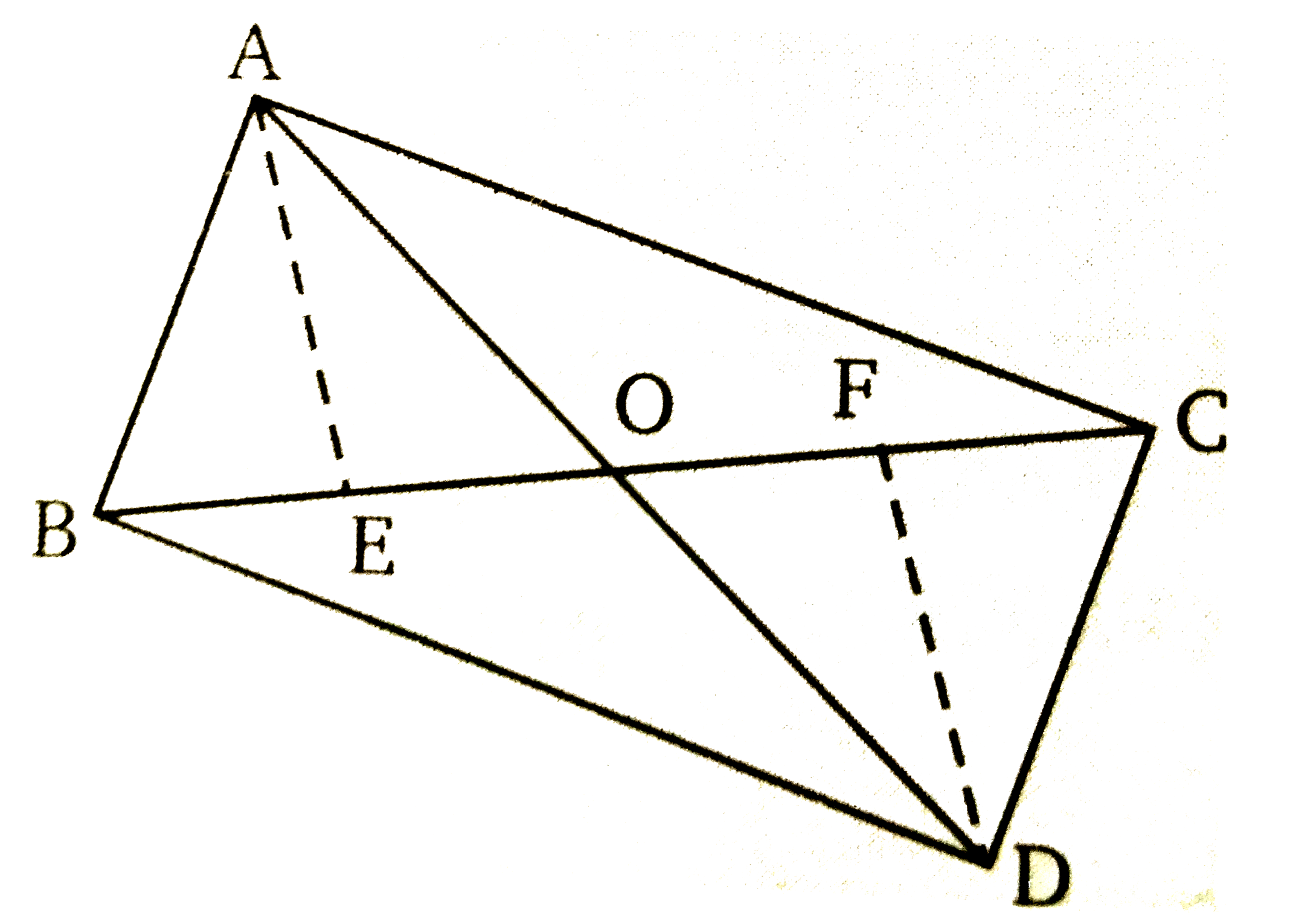
दो त्रिभुजों ABC व DBC के आधार समान हैं तथा सम्मुख भुजा BC पर शीर्ष A व D इस प्रकार हैं कि ar(ΔABC)=ar(ΔDBC)। सिद्ध कीजिए कि BC, रेखा AD को समद्विभाजित करती है।
उपपत्ति : हम जानते हैं कि त्रिभुज ABC व DBC के क्षेत्रफल समान तथा आधार BC उभयनिष्ठ है। इसलिए BC के संगत शीर्षलम्ब भी बराबर होगें।
⇒AE=DF
अब ΔAEO व ΔDFO में
∠AOE=∠DOF ( ∵ शीर्षाभिमुख कोण)
∠AEO=∠DFO=90∘
AE=DF
ΔAEO≅ΔDFO ( AAS सर्वांगसमता से)
⇒AO=DO
⇒BC रेखा AD को समद्विभाजित करती है।
Topper's Solved these Questions
- BOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - अति लघु उत्तरीय प्रश्न5videos
समांतर चतुर्भुज व त्रिभुज के क्षेत्रफल
- BOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - लघु उत्तरीय प्रश्न16videos
समांतर चतुर्भुज व त्रिभुज के क्षेत्रफल
- BOOK - BALAJI PUBLICATIONCHAPTER - शेषफल प्रमेय तथा गुणनखण्ड प्रमेय EXERCISE - स्वमूल्यांकन परिक्षण20videos
शेषफल प्रमेय तथा गुणनखण्ड प्रमेय
- BOOK - BALAJI PUBLICATIONCHAPTER - सांख्यिकीEXERCISE - स्वमूल्यांकन परीक्षण17videos
सांख्यिकी
Similar Questions
एक समांतर चतुर्भुज के विकर्ण इसे कितने भागों में विभक्त करते हैं?
04:36View Solutionचित्र (i) और (ii) में दिए गये समलम्ब चतुर्भुजों ABCD और PQRS का क्षेत्रफल ज्ञात कीजिए।

06:49View Solutionx3+3x2+3x+1 को 5+2x से भाग करने पर शेषफल ज्ञात कीजिए।
07:01View Solutionतीन सिक्के 30 बार उछाले गये। प्रत्येक बार आये चित् की संख्या निम्न प्रकार लिखी गयी :
0,1,2,2,1,2,3,1,3,0,1,3,1,1,2,2,0,1,2,1,3,0,0,1,1,2,3,2,2,0
उपरोक्त आँकड़ों के लिए एक बारंबारता बंटन सारणी तैयार कीजिए।03:37View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that (ar (ABC))/( ar (DBC))= (AO )/( DO )
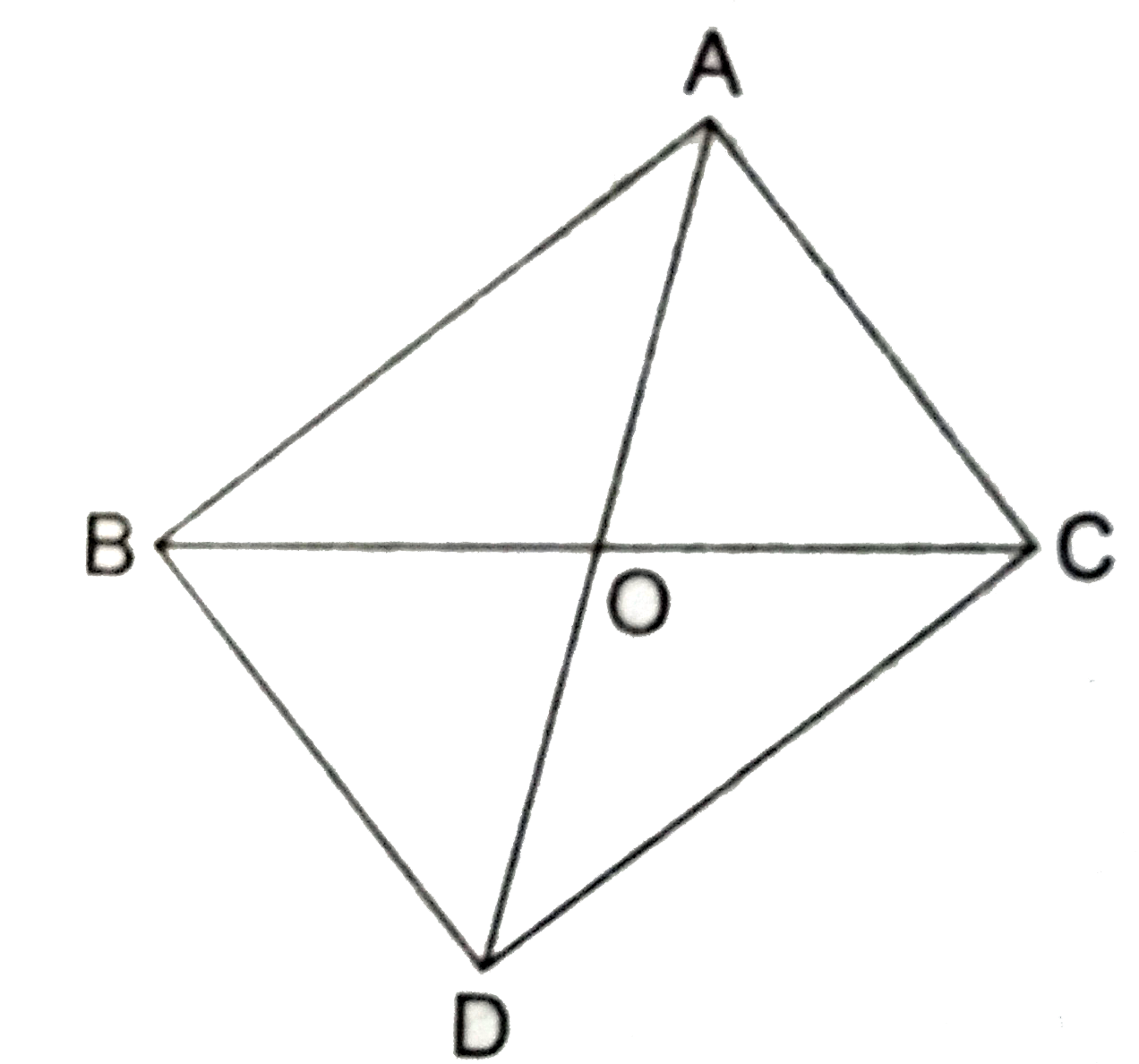
03:37View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
 02:34View Solution
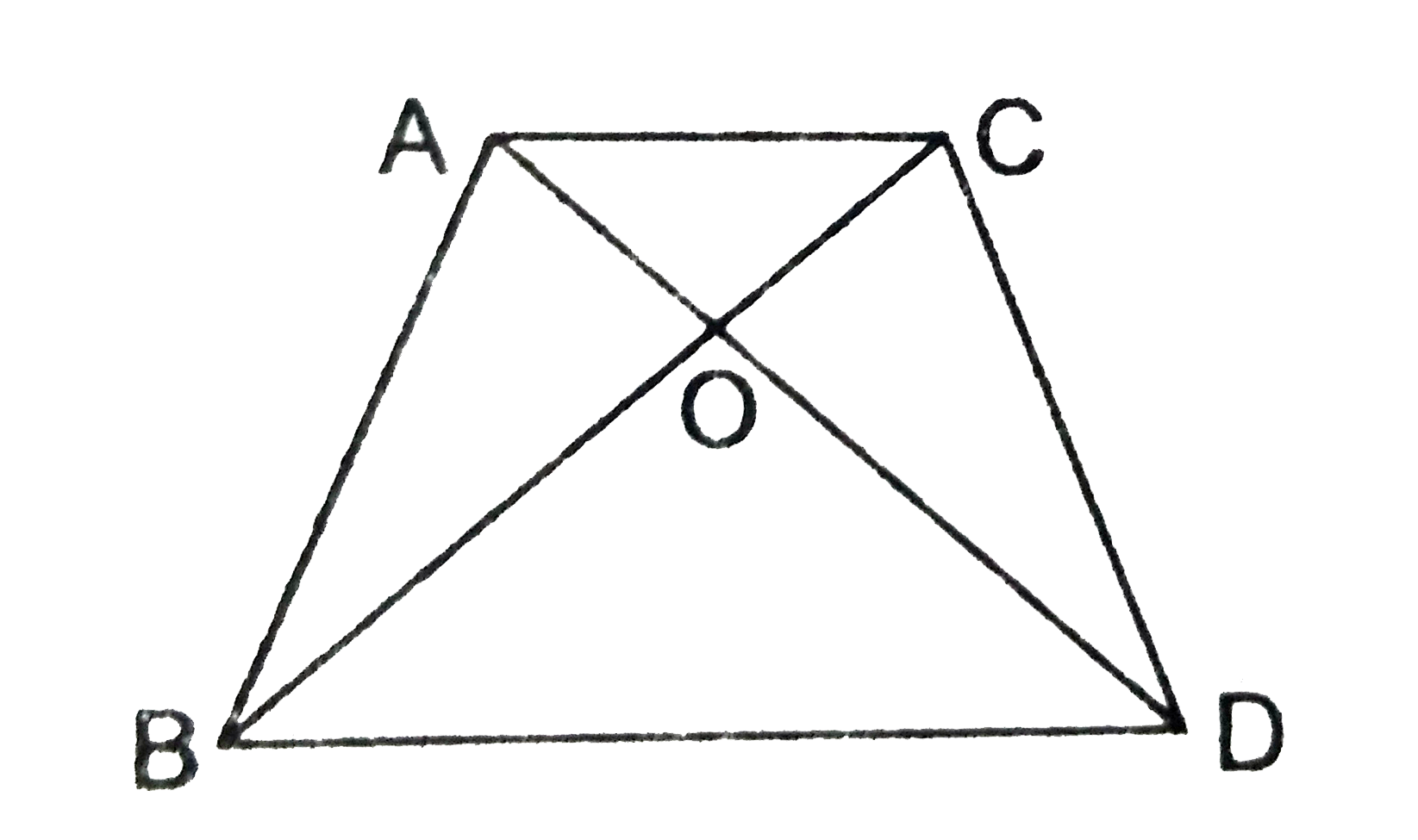
02:34View Solutionआकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
 03:03View Solution
03:03View Solutionएक ही आधार BC पर दो त्रिभुज ABC तथा DBC इस प्रकार स्थित है कि बिंदु A तथा D रेखा BC के विपरीत दिशाओं में है। यदि ar(ΔABC)=ar(ΔDBC) हो, तो दर्शाइए कि BC रेखा AD को समद्विभाजित करती है।
06:09View Solutionमाना ABC व DBC समान आधार BC पर दो त्रिभुज हैं। BC की विपरीत दिशा से A व D बिंदु इस प्रकार हैं कि ar(ΔABC)=ar(ΔDBC)। सिद्ध कीजिए यह BC,AD को समद्विभाजित करती है।
07:39View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
03:21View Solutionयदि ΔABC~ΔPQR तथा BC=5QR तो ar(ΔABC):ar(ΔPQR) है
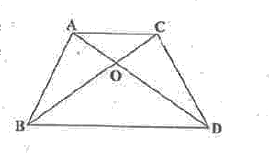
04:36View SolutionIn Fig , ABC and DBC are two triangles on the same base BC. If AD intersects BC,at O , show that ar(ABC)ar(DBC)=AODO
 02:50View Solution
02:50View Solutionसदिशों के प्रयोग द्वार सिद्ध कीजिए कि बिंदु A(−2,3,5),B(7,0,−1),C(−3,−2,−5) और D(3,4,7) इस प्रकार हैं कि AB और CD बिंदु P(1,2,3) पर प्रतिच्छेद करते हैं।
02:20View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
02:39View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
07:35View Solution

