चित्र 14.28 में ABCD समान्तर चतुर्भुज है जिसमे ∠DAB=60∘ है। यदि ∠A तथा ∠B के अर्धक क्रमशः AP तथा BP रेखा CD पर बिंदु P पर मिलते है, तो सिद्ध कीजिए की CD का मध्य-बिंदु P है।
दिया है की ∠DAB=60∘
∴∠A+∠B=180∘
∴60∘+∠B=120∘ ltbgt ⇒∠B=120∘
अब AB∣∣DC तथा तिर्यक रेखा AP इन्हे प्रतिच्छेदित करती है।
∴∠PAB=∠APD
⇒∠APD=30∘ [∴∠PAB=30∘]
अतः ΔAPD में
∠PAD=∠APD [ प्रत्येक कोण 90∘]
⇒AD=PD ...(i)[∴ बराबर भुजाओं की सम्मुख कोण बराबर होते है]
चूँकि ∠B का अर्धक BP है।
∴∠ABP=∠PBC=60∘
अब AB∣∣DC तथा एक तिर्यक रेखा BP इन्हे प्रतिच्छेद करती है।
⇒CPB=60∘ [∴∠ABP=60∘]
अतः ΔCBP में
∠CBP=∠CPB [प्रत्येक कोण 60∘]
⇒CP=BC [∴ बराबर कोनों की सम्मुख भुजाएं बराबर होती है]
⇒CP=AD [∴ABCD एक ∣∣gm है, AD=BC]....(ii)
(i) तथा (ii) से
PD=CP
⇒CD का मध्य-बिंदु P है। ltbr 
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.14videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.216videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न22videos
घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन
- BOOK - RD SHARMACHAPTER - त्रिभुज तथा उसके कोण EXERCISE - बहु विकल्पीय प्रश्न28videos
त्रिभुज तथा उसके कोण
Similar Questions
एक चतुभुर्ज है तीन कोण क्रमशः 110∘,50∘ तथा 40∘ है। इसका चौथा कोण ज्ञात कीजिए।
04:29View Solutionएक समान्तर चतुर्भुज के दो सम्मुख कोण (3x−2)∘ तथा (50−x)∘ है। समान्तर चतुभुर्ज के प्रत्येक कोण की माप ज्ञात कीजिए?
03:05View Solutionयदि किसी घनाभ के तीन आसन्न फलकों के क्षेत्रफल A1,A2 व A3 से दर्शाया जावे तो इस घनाभ का आयतन होगा :
05:01View Solutionयदि किसी त्रिभुज के तीनो कोण बराबर हो, तो प्रत्येक कोण का माप होगा:
02:15View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
03:29View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
03:29View Solutionबिंदु A(1,2) से होकर जाने वाली रेखा X-अक्ष के साथ 60∘ का कोण बनाती है तथा x+y=6 को बिंदु P पर काटती है तो AP की लम्बाई ज्ञात कीजिए
02:10View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
05:42View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
03:01View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
02:52View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
04:21View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
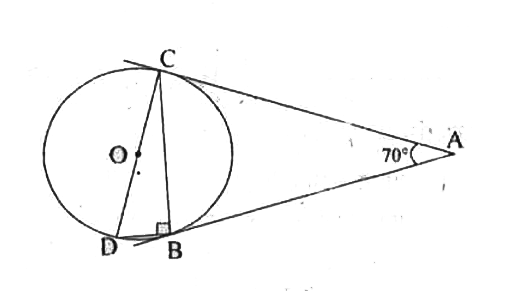
03:38View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
 04:39View Solution
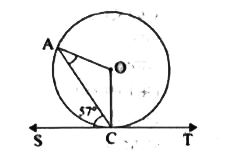
04:39View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
 04:24View Solution
04:24View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
04:44View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
06:22View Solution

