यदि किसी चतुभुर्ज के बराबर हो तथा एक दूसरे को समकोण पर संदुभाजित करते हो, तो वह एक वर्ग होगा।
माना की ABCD एक चतुर्भुर्जों है जिसके विकर्ण AC तथा BD बराबर है, तो एक दूसरे को समकोण पर समद्विभाजित करते है। सिद्ध करना है की यह एक वर्ग है। इसके लिए हमे यह दर्शाता होगा की
∠A=∠B=∠C=∠D90∘ तथा AB=BC=CD=DA
चूँकि चतुभुर्ज ABCD के विकर्ण AC और BD एक दूसरे को समद्विभाजति करते है। अतः यह एक समांतर चतुभुर्ज है।
AB=DC एवं BC=AD
ΔAOB एवं ΔCOB पर विचार करते है। इन दोनों त्रिभुजों में
OA=OC [∴O,AC का मध्य बिंदु है]
∠AOB=∠COB [ प्रत्येक 90∘ के बराबर है]
तथा OB=OB [ उभयनिष्ठ]
ΔAOB≅ΔCOB
⇒AB=CB [ c.p.c.t. से]
किन्तु AB=DC तथा BC=AD
∴AB=BC=CD=DA
अब त्रिभुज BAD एवं CDA में,
BA=CD
AD=DA
तथा BD=AC [दिया है]
अतः, भुजा-कोण-भुजा सर्वांगसमता अभिगृहित से,
ΔBAD≅ΔCDA
⇒∠A=−∠D
लेकिन ∠A+∠=180∘ [ ∴ तिर्यक रेखा के एक ही ओर क्रमागत अन्तः कोणों का योग 180∘ होता है]
∴∠A+∠A=180∘⇒∠A=90∘ [∴∠A=∠D]
⇒∠A=∠D
∴∠A=∠D=90∘
इसी प्रकार हम सिद्ध कर सकते है की ∠B=∠C=90∘ है।
∴∠A=∠B=∠C=∠D=90∘
अतः ABCD एक वर्ग है।

Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.14videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.216videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न22videos
घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन
- BOOK - RD SHARMACHAPTER - त्रिभुज तथा उसके कोण EXERCISE - बहु विकल्पीय प्रश्न28videos
त्रिभुज तथा उसके कोण
Similar Questions
एक चतुभुर्ज है तीन कोण क्रमशः 110∘,50∘ तथा 40∘ है। इसका चौथा कोण ज्ञात कीजिए।
01:19View Solutionएक समान्तर चतुर्भुज के दो सम्मुख कोण (3x−2)∘ तथा (50−x)∘ है। समान्तर चतुभुर्ज के प्रत्येक कोण की माप ज्ञात कीजिए?
03:18View Solutionयदि किसी घनाभ के तीन आसन्न फलकों के क्षेत्रफल A1,A2 व A3 से दर्शाया जावे तो इस घनाभ का आयतन होगा :
06:19View Solutionयदि किसी त्रिभुज के तीनो कोण बराबर हो, तो प्रत्येक कोण का माप होगा:
04:33View Solutionयदि दो वृतो की त्रिज्याएँ क्रमशः r1 व r2 है और वे एक - दूसरे को बाह्यतः स्पर्शः करते हो , तो -
06:02View Solutionयदि तो संख्याएँ a तथा b दी गयी हो तो इनका गुणनफल किसके बराबर होता है ?
01:35View Solutionयदि किसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,0),(1,3) और (-1,2) हो तो उसके कोणों को ज्ञात कीजिए।
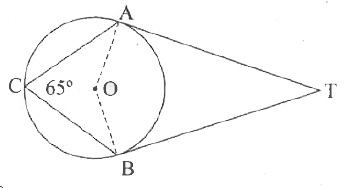
03:50View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
 01:36View Solution
01:36View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -
 03:21View Solution
03:21View Solutionयदि A तथा B व्यत्क्रमणीय हो, तो
03:05View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
03:00View Solutionयदि समीकरण x2+2mx+m2−2m+6=0 के मूल बराबर हो, तो m का मान होगा।
03:00View Solutionयदि α,β द्विघात समीकरण x2+px+p3=0(p≠0) के मूल हो तथा (α,β) परवलय y2=x पर स्थित एक बिंदु हो, तो समीकरण के मूल होगा
03:00View Solutionयदि सदिश a तथा b रेखीय स्वतन्त्र हो तथा (√3tanθ+1)a+(√3secθ−2)b=0 को सन्तुष्ट करते हो, तब θ का मान होगा
View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
01:53View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3, 4) और केन्द्र (2,3) हो, तो दूसरे सिरे का निर्देशांक ज्ञात कीजिए।
38:27View Solution

