चित्र 14.93 में ABCD एक सम्लब है जिसमे भुजा AB भुजा DC के समान्तर है तथा E भुजा AD का मध्य-बिन्दु है। यदि भुजा BC पर BC बिन्दु पर इस प्रकार है की रेखाखण्ड EF भुजा DC के समान्तर है, तो सिद्ध कीजिए की EF=12(AB+DC)
दिया है : एक समलम्ब ABCD जिसमे AB∣∣DC,AD का मध्य-बिन्दु E है। तथा भुजा BC पर एक बिन्दु F एक बिन्दु इस प्रकार है की EF∣∣DC.

सिद्ध करना है EF=12(AB+DC)
उपपत्ति ΔADC में AD का मध्य-बिन्दु E है तथा EG∣∣DC (दिया है)
∴AC का मध्य-बिन्दु G है
क्योकिं किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाले रेखाखण्ड तीसरी भुजा का आधा होता है।
∴AG=12DC ....(i)
अब ABCD एक सम्लब चतुभुर्ज है जिसमे AB∣∣DC
परन्तु EF∣∣DC
∴EF∣∣AB
⇒GF∣∣AB
ΔABC में AC का मध्य बिन्दु G है। (सिद्ध किया है) तथा GF∣∣AB
∴BC का मध्य बिन्दु F है
⇒G=12AB ...(ii)[∴ त्रिभुज की किन्ही दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा का आधा होता है]
(i) तथा (ii) से, हमारे पास है,
EG+GF=12(DC)+12(AB)⇒EF=12(AB+DC)
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.14videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.216videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न22videos
घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन
- BOOK - RD SHARMACHAPTER - त्रिभुज तथा उसके कोण EXERCISE - बहु विकल्पीय प्रश्न28videos
त्रिभुज तथा उसके कोण
Similar Questions
एक चतुभुर्ज है तीन कोण क्रमशः 110∘,50∘ तथा 40∘ है। इसका चौथा कोण ज्ञात कीजिए।
04:39View Solutionएक समान्तर चतुर्भुज के दो सम्मुख कोण (3x−2)∘ तथा (50−x)∘ है। समान्तर चतुभुर्ज के प्रत्येक कोण की माप ज्ञात कीजिए?
05:05View Solutionयदि किसी घनाभ के तीन आसन्न फलकों के क्षेत्रफल A1,A2 व A3 से दर्शाया जावे तो इस घनाभ का आयतन होगा :
04:32View Solutionयदि किसी त्रिभुज के तीनो कोण बराबर हो, तो प्रत्येक कोण का माप होगा:
02:26View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
02:30View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
04:56View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
03:05View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
01:42View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
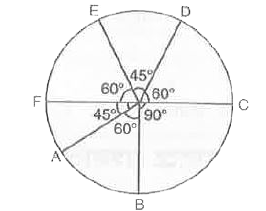
05:38View Solutionनिम्नलिखित के उत्तर दीजिए और उनके कारण भी दीजिए :
(i ) क्या AB = BC है?
(ii ) क्या AB = DC है?
(iii ) क्या DE = AF है?
(iv ) क्या EF = AB है?
(v ) क्या BC = EF है?
(vi ) क्या AB = DC = EF है?
 04:14View Solution
04:14View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
02:25View Solutionयदि किसी घन का आयतन 125cm3 है, तो उसकी भुजा की लम्बाई क्या होगी?
04:05View SolutionIn the given figure, ABCD is a square of side 14cm. E and F are mid points of sides AB and DC respectively. EPF is a semicircle whose diameter is EF. LMNO is a square. What is the area (in cm^2 ) of the shaded region? दी गई आकृति में, ABCD 14 सेमी. भुजा वाला एक वर्ग है। E तथा F क्रमश: AB तथा DC भुजा के मध्य बिन्दु है। EPF, एक अर्धवृत्त है जिसका व्यास EF है। LMNO एक वर्ग है। छायांकित भाग का क्षेत्रफल ( सेमी^2 में) क्या है?
04:00View SolutionIn the given, ABCDEF is a regular hexagon of side 12cm. P, Q and R are the mid points of the sides AB, CD and EF respectively. What is the area (in cm^2 ) of triangle PQR? दी गई आकृति में , ABCDEF एक सम षट्भुज है जिसकी भुजा 12 से.मी.? है। P, Q तथा R क्रमशः भुजाओं AB, CD तथा EF के मध्य बिन्दु है। त्रिभुज PQR का क्षेत्रफल ( से.मी.^2 में) क्या है?
01:40View SolutionABCD is a rectangle P is point on the side AB as shown in the given figure. If DP = 13, CP = 10 and BP = 6, then what is the value of AP?
ABCD एक आयत है। P, भुजा AB पर एक बिन्दु है जैसा की दी गई आकृति में दर्शाया गया है। यदि DP = 13, CP = 10 तथा BP = 6 हो, तो AP का मान क्या है?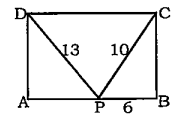 01:05View Solution
01:05View SolutionABC is a triangle. AB =10cm and BC=16 cm AD=8 cm and is perpendicular to side BC. What is the length (in cm) of side AC? ABC एक त्रिभुज है। AB =10 सेमी तथा BC=16 सेमी है। AD=8 सेमी है तथा यह भुजा BC के समलम्ब है। भुजा AC का मान (सेमी. में) क्या है?
02:03View Solution

