सिद्ध कीजिए कि आयत संलग्न भुजाओं के मध्य बिंदुओं को मिलाने से बना चतुर्भुज समचतुर्भुज होता है।

माना ABCD एक आयत है जिसकी भुजाओं AB,BC,CD और DA के मध्य बिंदु क्रमशः P,Q,R और S है।
ΔBAC में
P और Q क्रमशः BA और BC के मध्य बिंदु है।
∴PQ∣∣AC और PQ=12AC…………..1
ΔADC में
R और S क्रमशः DC और DA के मध्य बिंदु है।
SR∣∣AC और SR=12AC…………….2
समीकरण 1 और 2 से
PQ∣∣SR और PQ=SR…………….3
⇒□PQRS एक समांतर चतुर्भुज है।
अब ABCD एक आयत है।
∴AD=BC
⇒12AD=12BC
⇒AS=BQ………..4
ΔAPS और ΔBPQ में
AP=BP (P,AB का मध्य बिंदु है।)
∠PLAS=∠PBQ ( प्रत्येक 90∘)
∴ΔAPS=ΔBPQ [समीकरण 4 से]
⇒PS=PQ .......5 (S.A.S प्रमेय)
समीकरण 3 और 5 से
∴PQRS एक समचतुर्भुज है।
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8A27videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8B15videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न5videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )8videos
त्रिभुज
Similar Questions
एक चतुर्भुज के दो कोणों 89∘ और 113∘ है। यदि अन्य दो कोण बराबर है तो बराबर कोणों को ज्ञात कीजिए।
01:37View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।06:07View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
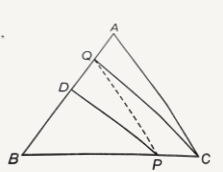 02:11View Solution
02:11View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
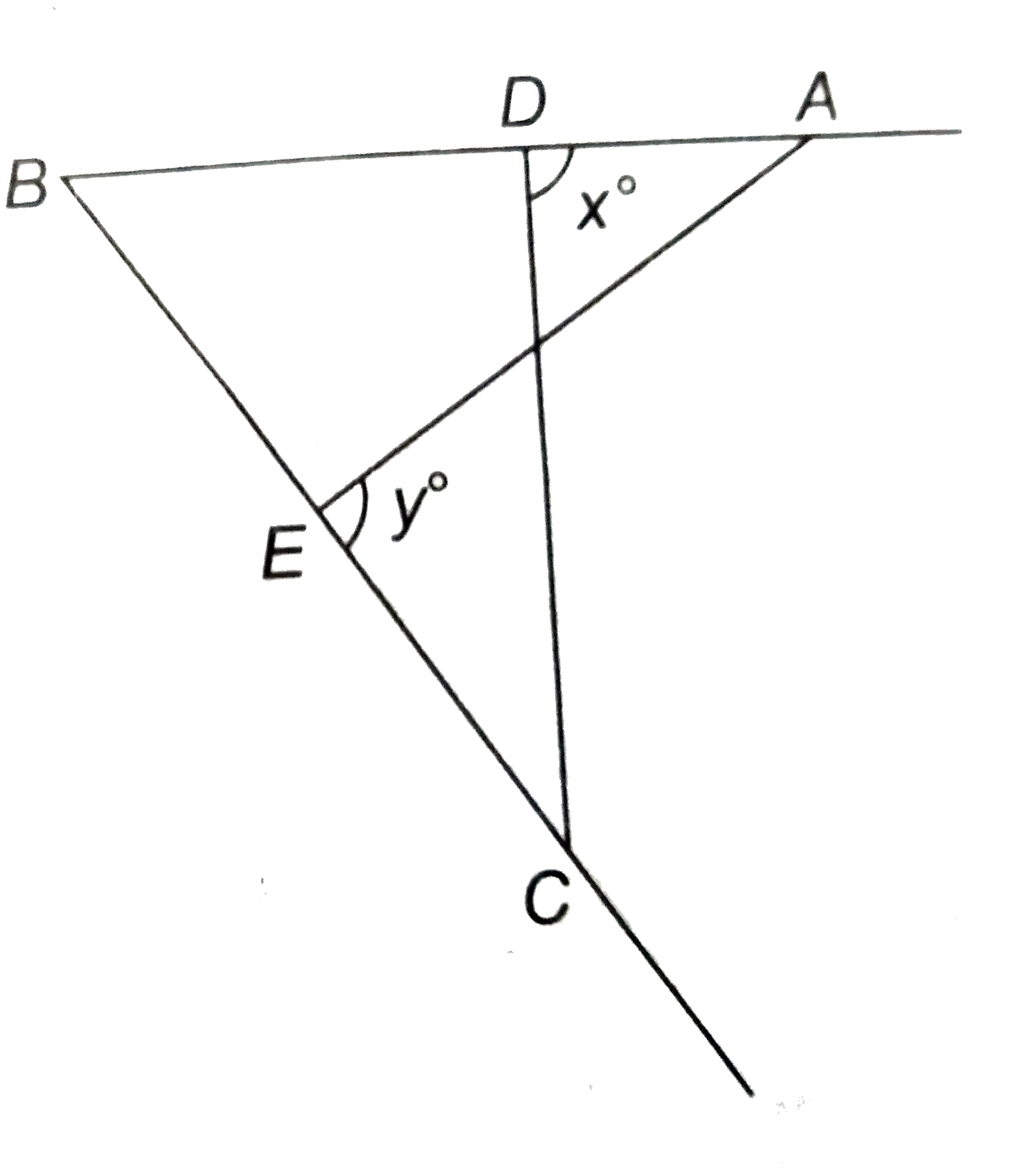 01:31View Solution
01:31View SolutionHow many lines of symmetry does the above figure have ?
02:45View SolutionWhich of the following are correct chain isomers of butane ? (i)
02:17View SolutionDetermine the point of symmetry of a regular hexagon.
05:41View SolutionDtermine the images of the following figure about the given line :
02:21View SolutionMatch the following Column A to Column B
 02:03View Solution
02:03View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionFind the area of the figure given below.
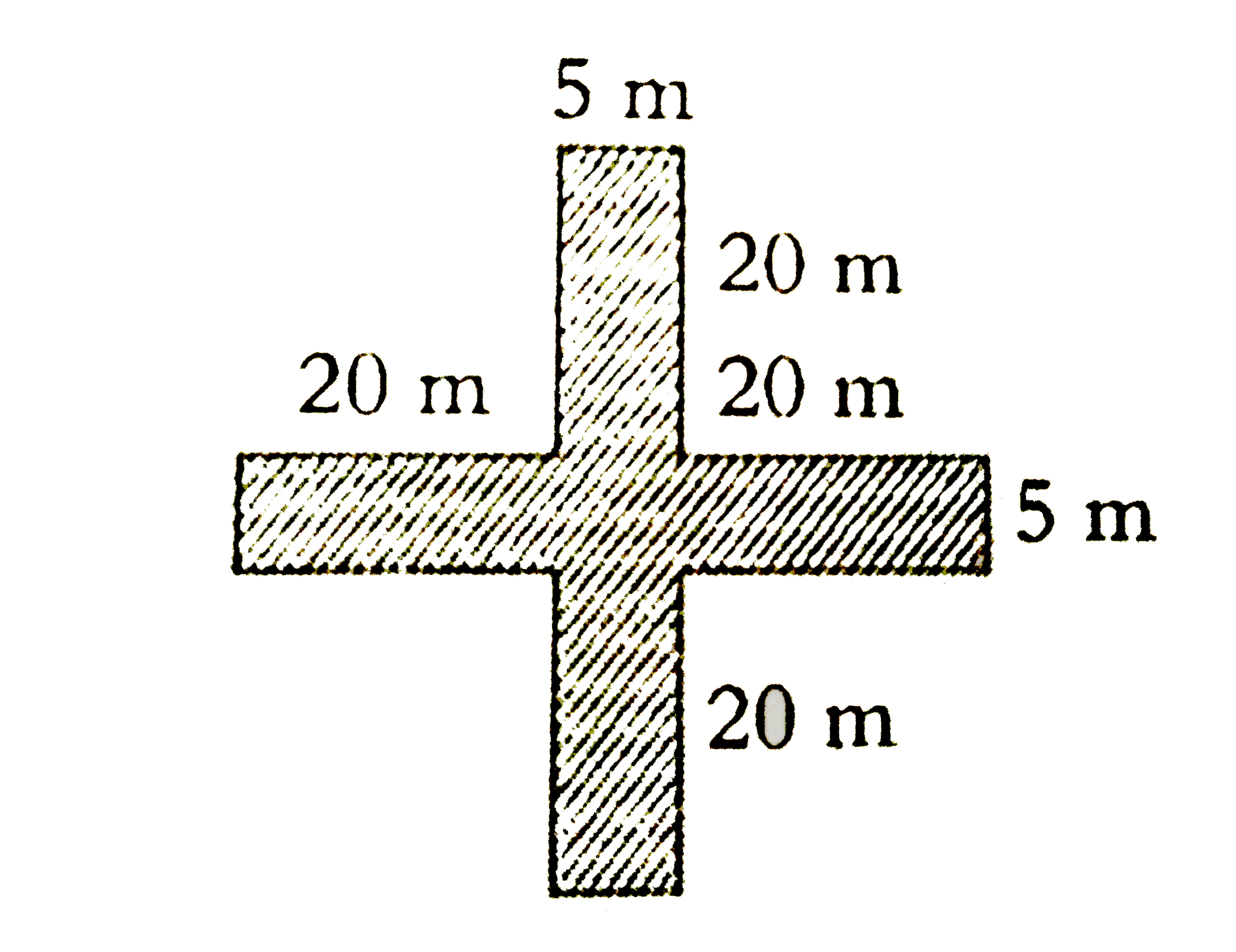 02:10View Solution
02:10View SolutionThe area of the shaded part in the figure given below is ______.
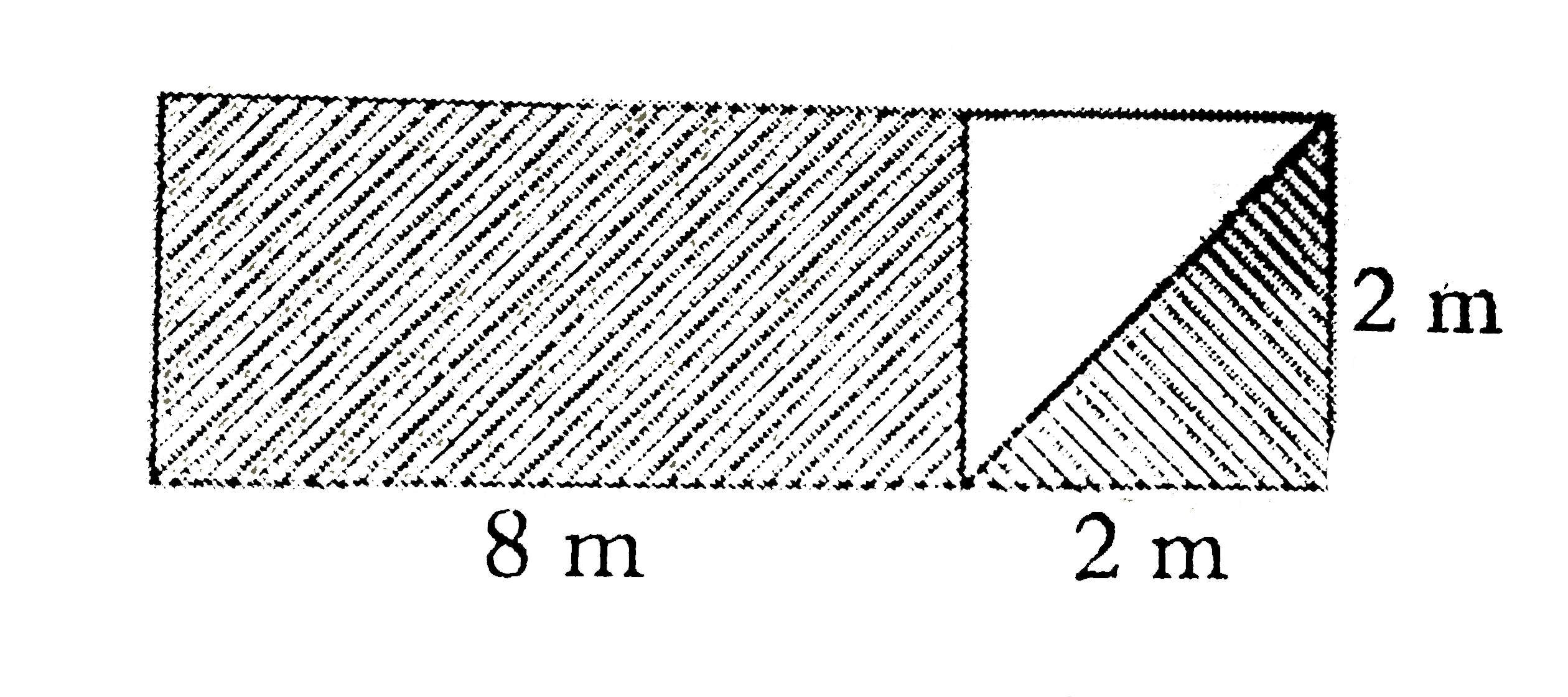 04:23View Solution
04:23View SolutionThe inequation represented by the graph given below is :
01:13View SolutionThe inequation that best describes the graph given below is _________
03:12View SolutionThe inequation that best describes the following graph is _________
05:46View Solution

