m द्रव्यमान का एक गोलक L लंबाई की हल्की दूरी से लटका हुआ है । इसके निम्नतम बिंदु A पर क्षैतिज वेग v0 इस प्रकार लगाया जाता है कि यह ऊर्ध्वाधर तल में अर्द्धवृत्ताकार प्रक्षेप्य पथ को इस प्रकार तय करता है कि दूरी केवल उच्चतम बिंदु C पर ढीली होती है , जैसा कि चित्र में दर्शाया गया है । निम्न राशियों के लिए व्यंजक प्राप्त कीजिए -
( a ) v0
( b ) बिंदुओं B तथा C पर गोलक की चाल तथा
( c ) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात (KBKC)
गोलक के बिंदु C पर पहुँचने के बाद पथ की आकृति पर टिपण्णी कीजिये ।
(a ) बिंदु A पर - गोलक की स्थितिज ऊर्जा शून्य होगी किन्तु गतिज ऊर्जा K=12mv(0)2

∴ बिंदु A पर कुल ऊर्जा E=0+12mv20
⇒ E=12mv20 ...(1)
गोलक की वृत्तीय गति के लिए
TA−mg=mv20L (अभिकेंद्र बल ) ...(2)
बिंदु C पर - गोलक की स्थितिज ऊर्जा =mg.2L=2mgL
तथा गतिज ऊर्जा =12mv2C, जहाँ vC बिंदु C पर चाल है।
∴ बिंदु C पर कुल ऊर्जा E=2mgL+12mv2C ...(3)
इस बिंदु पर वृत्तीय गति के लिए
mg=mv2CL [∴TC=0]
∴ mvC=mgL ....(4)
समी. (3 ) में मान रखने पर,
E=2mgL+12mgL
E=52mgL ....(5)
समी. (1 ) और समी. (5 ) से,
12mv20=52mgL ...(6)
Arr v0=√5gL
(b ) समी. (4 ) से,
v2C=gL
vC=√gL.
बिंदु B पर - गोलक कि कुल ऊर्जा E=mgL+12mv2B
समी. (1 ) से मान रखने पर,
12mv20=mgL+12mv2B
समी. (6 ) से मान रखने पर,
52mgL=mgL+12mv2B
⇒ v2B=3gL
⇒ vB=√3gL.
(c ) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात
KBKC=12mv2B12mv2C=v2Bv2C=3gLgL=31
⇒ KB:KC=3:1
बिंदु C पर गोलक का वेग बायीं ओर क्षैतिज दिशा में होता है । यदि इस बिंदु पर डोरी को काट दिया जाए तो गोलक की गति प्रक्षेप्य गति होगी अन्यथा इसकी गति वृत्तीय गति ही होगी ।
Topper's Solved these Questions
- कार्य, ऊर्जा और शक्ति BOOK - NAVBODHCHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - आंकिक उदाहरण प्लस
8 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NAVBODHCHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - बोधात्मक प्रश्न
5 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NAVBODHCHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
51 Videos
- कणों के निकाय की गति और घुर्णो गति BOOK - NAVBODHCHAPTER - कणों के निकाय की गति और घुर्णो गति EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
50 Videos
- गति के नियम BOOK - NAVBODHCHAPTER - गति के नियम EXERCISE - बहुविकल्पीय प्रश्न
53 Videos
Similar Questions
समान द्रव्यमान m के दो गुटके A और B भारहीन स्प्रिंग से जुड़े हैं। वे घर्षण रहित टेबल पर रखे गये हैं। स्प्रिंग का बल नियतांक k है। उसी द्रव्यमान का अन्य गुटका C गुटका A से v वेग से टकराता है। तब निम्न की गणना कीजिए -
(i ) जब स्प्रिंग अधिकतम संपीड़न की स्थिति में होता है तब निकाय (A - B ) की गतिज ऊर्जा ।
(ii ) स्प्रिंग का अधिकतम संपीडन।
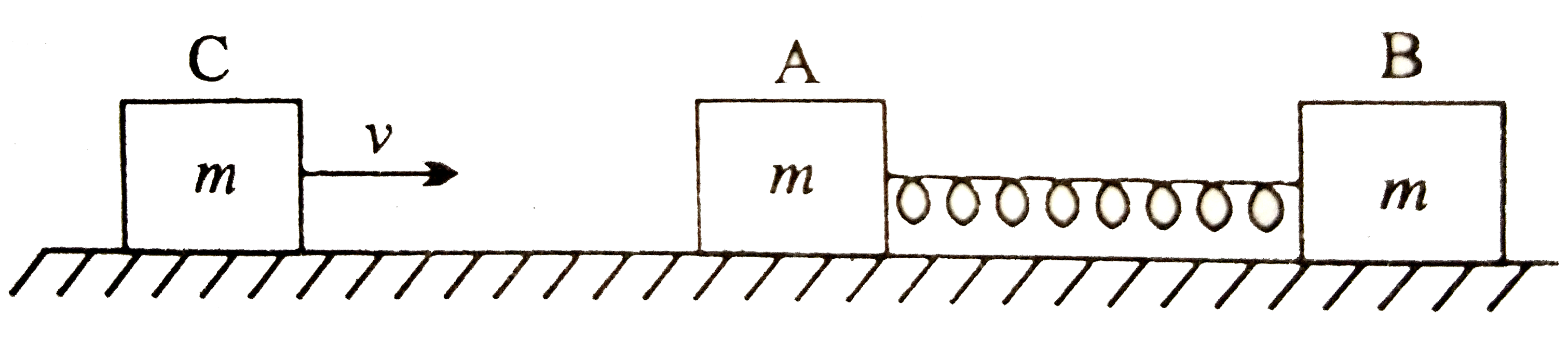
View Solutionएक पिंड एक बल के अधीन त्वरित गति कर रहा है । क्या यह संभव है कि बल द्वारा कोई कार्य नहीं किया जा रहा हो ? उदाहरण दीजिए ।
View Solutionकिसी वस्तु पर किसी बल द्वारा किए गए कार्य का चिह्व समझना महत्वपूर्ण है । सावधानीपूर्वक बताइए कि निम्न लिखित राशियाँ धनात्मक हैं या ऋणात्मक-
( a ) किसी व्यक्ति द्वारा किसी कुँए में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने में किया गया कार्य ।
View Solutionएकसमान द्रव्यमान घनत्व के निम्नलिखित पिंडों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए-
( a ) गोला, ( b ) सिलिंडर, ( c ) छल्ला तथा ( d ) घन ।
क्या किसी पिंड का द्रव्यमान केंद्र आवश्यक रूप से उस पिंड के भीतर स्थित होता है ?
View Solutionएक उत्थापक स्थिर चाल v से नीचे की ओर गिर रहा है । इसका एक यात्री एक सिक्के को गिरा देता है । सिक्के का फर्श की ओर त्वरण का मान -
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज ABC में A और B स्थिर बिंदु है । शीर्ष C इस प्रकार गमन करता है कि cotA+cotB=λ, जहाँ λ अचर है । C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु P का बिन्दुपथ ज्ञात कीजिए जो इस प्रकार गमन करता है कि बिंदु A(am,0),m≠1 से उसकी दूरी , बिंदु B(am,0) से उसकी दूरी की m गुनी रहती है ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु का बिन्दुपथ जो इस प्रकार गमन करता है कि बिंदु की दोनों अक्षों से दूरी सदैव समान रहती है ………… होगा ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solution
