विरामावस्था में किसी मुक्त न्यूट्रॉन के क्षय पर विचार कीजिए -
प्रदर्शित कीजिए कि इस प्रकार के द्विपिंड क्षय से नियत ऊर्जा का कोई इलेक्ट्रॉन अवश्य उत्सर्जित होना चाहिए और इसलिए यह किसी न्यूट्रॉन या किसी नाभिक के क्षय में प्रेक्षित सतत ऊर्जा वितरण का स्पष्टीकरण नहीं दे सकता ।
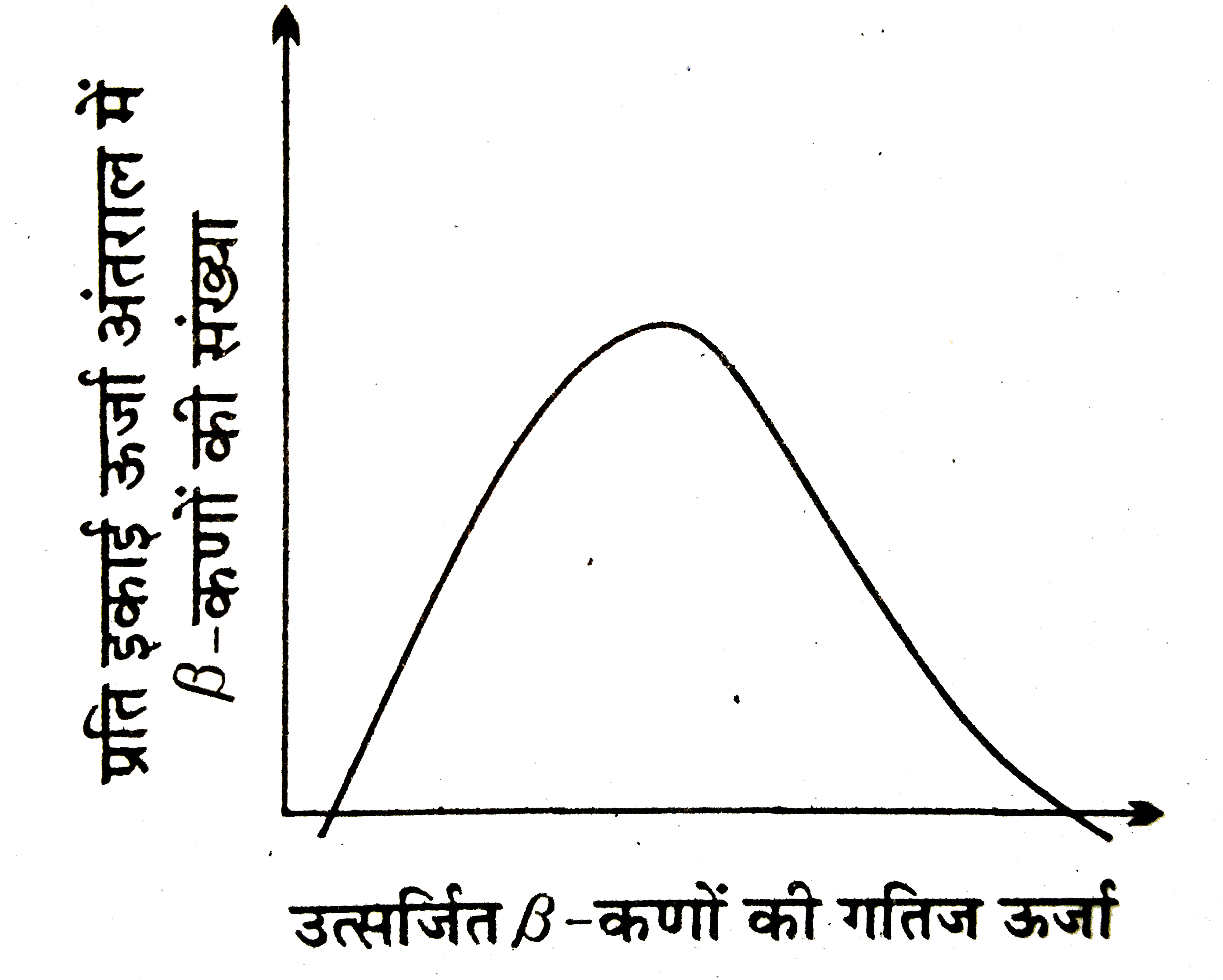
[नोट - इस अभ्यास का हल उन कई तर्कों में से एक है जिन्हें डब्ल्यू पॉली द्वारा क्षय के क्षय उत्पादों में किसी तीसरे कण के अस्तित्व का पूर्वानुमान करने के लिए दिया गया था । यह कण न्यूट्रिनो के नाम से जाना जाता है । अब हम जानते हैं कि यह निजी प्रचक्रण 1/2 ( जैस, p या n ) का कोई कण है । लेकिन यह उदासीन है या द्रव्यमानरहित या ( इलेक्ट्रॉन के द्रव्यमान की तुलना में ) इसका द्रव्यमान अत्यधिक कम है और जो द्रव्य के साथ दुर्बलता से परस्पर क्रिया करता है । न्यूट्रॉन की उचित क्षय - प्रक्रिया इस प्रकार है : ]
मानलो इलेक्ट्रॉन का द्रव्यमान व वेग है । इसी प्रकार प्रोटॉन का द्रव्यमान व वेग है ।
तब संवेग संरक्षण के नियम से ,
( इलेक्ट्रॉन प्रोट्रॉन ) का संवेग = न्यूट्रॉन का संवेग
या
स्पष्ट है कि इलेक्ट्रॉन और प्रोट्रॉन विपरीत दिशा में गति करेंगे । यदि इस क्रिया में द्रव्यमान क्षय हो, तो
जहाँ c = प्रकाश की चाल
या
या
या
या
इस समीकरण में दायीं और की सभी राशियाँ नियत हैं । अत : का मान भी नियत होगा । इस प्रकार इस क्षय से उत्सर्जित इलेक्ट्रॉन की ऊर्जा नियत होगी । अत : यह किसी न्यूट्रॉन या नाभिक के - क्षय में प्रेक्षित सतत ऊर्जा वितरण का स्पष्टीकरण नहीं दे सकता।
Topper's Solved these Questions
- कार्य, ऊर्जा और शक्ति BOOK - NAVBODHCHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - बहुविकल्पीय प्रश्न
80 Videos
- कणों के निकाय की गति और घुर्णो गति BOOK - NAVBODHCHAPTER - कणों के निकाय की गति और घुर्णो गति EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
50 Videos
- गति के नियम BOOK - NAVBODHCHAPTER - गति के नियम EXERCISE - बहुविकल्पीय प्रश्न
53 Videos
Similar Questions
6 मी/से की क्षैतिज चाल से चलता हुआ एक m द्रव्यमान का कण, उसी दिशा में 4 मी/से की चाल से चल रहे m द्रव्यमान के एक भारी कण से टक्कर करता है । यदि m < < m है तो टक्कर के बाद हल्के कण की चाल होगी, जबकि टक्कर पूर्ण प्रत्यास्थ हो -
View Solutionएकसमान द्रव्यमान घनत्व के निम्नलिखित पिंडों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए-
( a ) गोला, ( b ) सिलिंडर, ( c ) छल्ला तथा ( d ) घन ।
क्या किसी पिंड का द्रव्यमान केंद्र आवश्यक रूप से उस पिंड के भीतर स्थित होता है ?
View Solutionएक उत्थापक स्थिर चाल v से नीचे की ओर गिर रहा है । इसका एक यात्री एक सिक्के को गिरा देता है । सिक्के का फर्श की ओर त्वरण का मान -
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionऊर्जा के विभिन्न रूप | यांत्रिक ऊर्जा |गतिज ऊर्जा तथा स्थितिज ऊर्जा | संवेग और गतिज ऊर्जा में सम्बन्ध |किसी स्प्रिंग की स्थितिज ऊर्जा
View Solutionऊर्जा का परिचय |ऊर्जा के प्रकार
View Solutionट्रांसफार्मर मे ऊर्जा क्षय |डायनेमो
View Solutionसंधारित्र और परावैद्युत भरा हुआ संधारित्र में उष्मा का क्षय
View Solutionऊर्जा का परिचय #!#ऊर्जा के प्रकार
View Solutionरेडियो नाभिक 90234Th के दो क्रमिक β -क्षय के बाद एक -क्षय के माध्यम से एक नया रेडियो नाभिक प्राप्त किया जाता है। परिणामी रेडियो नाभिक का परमाणु क्रमांक और द्रव्यमान संख्या क्रमश: है:
View Solution""_ZX^A के रेडियोधर्मी क्षय में, निम्नलिखित में से किसे अशुद्ध कथन के रूप में माना जा सकता है?
View Solutionक्वांटम संख्या के निम्नलिखित समुच्चयों पर विचार कीजिए:

निम्नलिखित में से क्वांटम संख्या का कौन सा समुच्चय संभव नहीं है?
View Solutionनिम्नलिखित में से कौन-सा जल के साथ अभिक्रिया करने पर किसी भी गैसीय उत्पाद का उत्पादन नहीं करता है ?
View Solutionनिम्नलिखित में से कौन ओजोन परत के क्षय में सार्थक भूमिका निभाता है?
View Solution.....में मुख्य चरित्र कि किसी एक प्रमुख विशेषता का चित्रण होने के कारण अधिक विविधता और विस्तार नहीं होता |
View Solution
